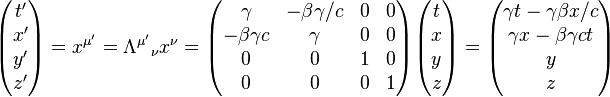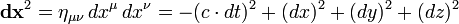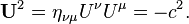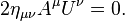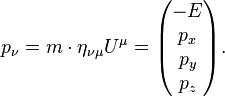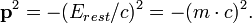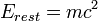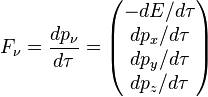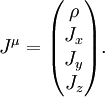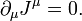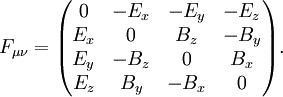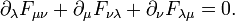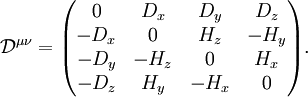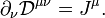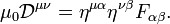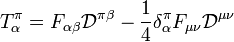A relatividade especial
Fundo para as escolas Wikipédia
Crianças SOS oferecem um download completo desta seleção para as escolas para uso em escolas intranets. Crianças SOS tem cuidado de crianças na África por 40 anos. Você pode ajudar o seu trabalho na África ?
A relatividade especial (SR) (também conhecida como a teoria da relatividade especial ou STR) é o teoria física da medição em sistemas de referência inerciais propostas em 1905 por Albert Einstein (após contribuições consideráveis de Hendrik Lorentz e Henri Poincaré) no jornal " Sobre a Eletrodinâmica dos Corpos em Movimento ". Ele generaliza Princípio da relatividade de Galileu - que todos movimento uniforme é relativo, e que não existe um estado absoluto e bem definido de descanso (sem quadros de referência privilegiados) - a partir de mecânica de toda a as leis da física, incluindo tanto as leis da mecânica e de eletrodinâmica, sejam elas quais forem. Além disso, a relatividade especial incorpora o princípio de que a velocidade da luz é a mesma para todos inercial observadores, independentemente do estado de movimento da fonte.
Esta teoria tem uma ampla gama de consequências que foram verificados experimentalmente. A relatividade especial derruba noções newtoniana de espaço e tempo absolutos , afirmando que o tempo e espaço são percebidos de forma diferente por observadores em diferentes estados de movimento. Ela produz a equivalência de matéria e energia , tal como expresso no fórmula de equivalência massa-energia E = mc 2, em que c é a velocidade da luz no vácuo. As previsões da relatividade especial concordam bem com a mecânica newtoniana em seu reino comum de aplicabilidade, especificamente em experimentos em que todas as velocidades são pequenos em comparação com a velocidade da luz.
A teoria é chamada de "especial" porque se aplica a princípio da relatividade só para referenciais inerciais. Einstein desenvolveu a relatividade geral de aplicar o princípio geral, ou seja, a qualquer quadro, e que a teoria inclui os efeitos da gravidade . Estritamente, a relatividade especial não pode ser aplicado na aceleração quadros ou em campos gravitacionais.
A relatividade especial revela que c não é apenas a velocidade de um determinado fenômeno, ou seja, a propagação da radiação eletromagnética (luz), mas sim uma característica fundamental do modo como o espaço eo tempo são unificados como espaço-tempo. Uma consequência disto é que não é possível para qualquer partícula que tem a massa a ser acelerado para a velocidade da luz.
Para a história e motivação, consulte o artigo: História da relatividade especial
Postulados
Em suas notas autobiográficas publicados em novembro de 1949 Einstein descreveu como ele tinha chegado aos dois postulados fundamentais sobre os quais ele baseia a teoria da relatividade especial. Depois de descrever em detalhe o estado de ambos os mecânicos e eletrodinâmica no início do século 20, ele escreveu
"Reflexões deste tipo deixou claro para mim há tanto tempo quanto logo após 1900, ou seja, pouco tempo após o trabalho pioneiro de Planck, que nem mecânica nem eletrodinâmica poderiam (exceto em casos limitante) afirmam validade exata. Aos poucos, eu me desesperava da possibilidade de descobrir as verdadeiras leis por meio de esforços construtivos baseados em fatos conhecidos. O mais longo e mais desesperadamente que eu tentava, mais cheguei à convicção de que só a descoberta de um princípio formal universal poderia nos levar a resultados seguros ... Como, então , poderia um tal princípio universal pode ser encontrada? "
Ele discerniu duas proposições fundamentais que pareciam ser os mais assegurada, independentemente da validade exata de tanto as leis (então) conhecidos da mecânica ou eletrodinâmica. Estas propostas foram (1) a constância da velocidade da luz, e (2) a independência das leis físicas (especialmente a constância da velocidade da luz) a partir da escolha do sistema de inércia. Em sua apresentação inicial da relatividade especial, em 1905, ele expressou estes postulados como:
- O Princípio da Relatividade - As leis pelas quais os estados de sistemas físicos são objecto de alterações não são afectados, se essas mudanças de estado ser encaminhado para um ou outro dos dois sistemas de coordenadas inerciais em movimento de translação uniforme.
- O Princípio da invariante Light Speed - luz no vácuo propaga com a velocidade c (a constante fixa) em termos de qualquer sistema de coordenadas inerciais, independentemente do estado de movimento da fonte de luz.
Deve notar-se que a derivação de relatividade especial depende não só nestes dois postulados explícitas, mas também em várias suposições tácita (que são feitas em quase todas as teorias da física), incluindo a isotropia e homogeneidade do espaço ea independência de medir as hastes e os relógios de sua história passada.
Após a apresentação original de Einstein da relatividade especial, em 1905, muitos conjuntos diferentes de postulados foram propostas em várias derivações alternativas. No entanto, o conjunto de postulados mais comum continua a ser aqueles empregados por Einstein em seu artigo original. Estes postulados referem-se à base do axiomático Transformação de Lorentz, que é o núcleo essencial da relatividade especial. Em todos os artigos de Einstein no qual ele apresentou derivações da transformação de Lorentz, ele baseou-lo sobre estes dois princípios.
Além dos papéis referenciados acima que dão derivações da transformação de Lorentz e descrever os fundamentos da relatividade especial-Einstein também escreveu pelo menos quatro papéis que dão argumentos heurísticos para a equivalência (e transmutabilidade) de massa e energia. (Note-se que esta equivalência não se segue das premissas básicas da relatividade especial. A primeira delas foi "Será que a inércia de um corpo depende do seu conteúdo de energia?", Em 1905. Neste e em cada um de seus três trabalhos posteriores sobre este assunto, Einstein aumentado os dois princípios fundamentais postulando as relações que envolvem força e energia das ondas eletromagnéticas implícitas pelas equações de Maxwell (o pressuposto de que, naturalmente, implica, entre outras coisas, a hipótese de a constância da velocidade da luz). Ele reconheceu em seu 1907 papel levantamento sobre a relatividade especial que era problemático para contar com as equações de Maxwell para o argumento de massa-energia heurística, e é por isso que ele sempre baseou a derivação de invariância de Lorentz (o núcleo essencial da relatividade especial) apenas na dois princípios básicos da relatividade e da invariância da velocidade da luz. Ele escreveu
"A idéia fundamental para a teoria da relatividade especial é este: A relatividade pressupostos e invariância velocidade da luz são compatíveis se as relações de um novo tipo (" transformação de Lorentz ") são postuladas para a conversão de coordenadas e horários de eventos ... O universal princípio da teoria da relatividade especial está contida no postulado:. As leis da física são invariantes em relação às transformações de Lorentz (para a transição de um sistema inercial a qualquer outro sistema inercial escolhido arbitrariamente) Este é um princípio de limitação de leis naturais. .. "
Assim, muitos tratamentos modernos da base de relatividade especial-lo no único postulado da covariância de Lorentz universal, ou, equivalente, no único postulado de Minkowski espaço-tempo.
Consequências
Einstein disse que todas as conseqüências da relatividade especial pode ser derivada da análise da Transformações de Lorentz.
Essas transformações, e, portanto, a relatividade especial, levar a previsões diferentes físicas do que a mecânica newtoniana quando velocidades relativas tornar-se comparável à velocidade da luz. A velocidade da luz é muito maior do que qualquer coisa que os seres humanos encontram alguns dos efeitos previstos pela relatividade são inicialmente contra-intuitiva:
- Tempo de dilatação - o lapso de tempo entre dois eventos não é invariante de um observador para outro, mas é dependente das velocidades relativas dos referenciais dos observadores (por exemplo, a paradoxo dos gêmeos que diz respeito a um gêmeo que voa em uma nave espacial viajando perto da velocidade da luz e retorna ao descobrir que seu irmão gêmeo envelheceu muito mais).
- Relatividade da simultaneidade - dois eventos que acontecem em dois locais diferentes que ocorrem simultaneamente com um observador, pode ocorrer em momentos diferentes para um outro observador (falta de simultaneidade absoluta).
- Contração de Lorentz - as dimensões (por exemplo, comprimento) de um objecto tal como medido por um observador pode ser menor do que os resultados de medições do mesmo objecto feitas por outro observador (por exemplo, a paradoxo escada envolve uma escada longa viajando perto da velocidade da luz e a ser contido dentro de uma garagem menor).
- Composição de velocidades - velocidades (e velocidades) não simplesmente "adicionar", por exemplo, se um foguete está se movendo em ⅔ a velocidade da luz em relação a um observador, eo foguete dispara um míssil contra ⅔ da velocidade da luz em relação ao foguete, o míssil não exceda a velocidade da luz em relação ao observador. (Neste exemplo, o observador vê que o míssil de viagens com uma velocidade de 12/13 a velocidade da luz).
- Inércia e impulso - como a velocidade de um objeto se aproxima da velocidade da luz, do ponto de vista de um observador, a sua massa parece aumentar, assim, tornando-se mais e mais difícil para acelerá-lo de dentro de quadro do observador de referência.
- Equivalência de massa e energia , E = mc 2 - O conteúdo energético de um objeto em repouso com massa m é igual a
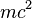 . Conservação de energia implica que, em qualquer uma reacção de redução da soma das massas de partículas deve ser acompanhada por um aumento da energia cinética das partículas após a reacção. Da mesma forma, a massa de um objecto pode ser aumentada tendo em energias cinéticas.
. Conservação de energia implica que, em qualquer uma reacção de redução da soma das massas de partículas deve ser acompanhada por um aumento da energia cinética das partículas após a reacção. Da mesma forma, a massa de um objecto pode ser aumentada tendo em energias cinéticas.
Simultaneidade
Desde a primeira equação da transformação de Lorentz em termos de diferenças de coordenadas
é evidente que dois eventos que são simultânea no quadro S (satisfazendo 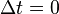 ), Não são, necessariamente simultâneos em outro referencial inercial S '(satisfazendo
), Não são, necessariamente simultâneos em outro referencial inercial S '(satisfazendo 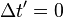 ). Só se esses eventos são colocal no quadro S (satisfazendo
). Só se esses eventos são colocal no quadro S (satisfazendo 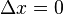 ), Que será simultânea num outro referencial S '.
), Que será simultânea num outro referencial S '.
Dilatação do tempo ea contração do comprimento
Escrevendo a transformação de Lorentz e sua inversa em termos de diferenças de coordenadas que obtemos
e
Suponha que temos um relógio em repouso no sistema unprimed S. Dois carrapatos consecutivos de este relógio são, então, caracterizada por 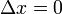 . Se queremos saber a relação entre os tempos entre estes carrapatos como medidos em ambos os sistemas, podemos usar a primeira equação e encontrar:
. Se queremos saber a relação entre os tempos entre estes carrapatos como medidos em ambos os sistemas, podemos usar a primeira equação e encontrar:
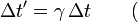 para eventos que satisfaçam
para eventos que satisfaçam 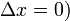
Isso mostra que o momento 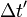 entre os dois carrapatos como pode ser visto na "movimento" referencial S 'é maior do que o tempo
entre os dois carrapatos como pode ser visto na "movimento" referencial S 'é maior do que o tempo 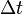 entre estes carrapatos como medido no quadro resto do relógio. Este fenômeno é chamado dilatação do tempo.
entre estes carrapatos como medido no quadro resto do relógio. Este fenômeno é chamado dilatação do tempo.
Da mesma forma, suponha que temos um haste de medição em repouso no sistema unprimed. Neste sistema, o comprimento da haste é escrito como 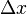 . Se queremos encontrar o comprimento desta haste medido no 'movimento' sistema S ', devemos certificar-se de medir as distâncias
. Se queremos encontrar o comprimento desta haste medido no 'movimento' sistema S ', devemos certificar-se de medir as distâncias 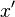 para os pontos finais da haste simultaneamente no quadro aprontado S '. Em outras palavras, a medição é caracterizado por
para os pontos finais da haste simultaneamente no quadro aprontado S '. Em outras palavras, a medição é caracterizado por 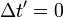 , Que podem combinar com o quarto equação para encontrar a relação entre os comprimentos
, Que podem combinar com o quarto equação para encontrar a relação entre os comprimentos 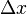 e
e 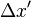 :
:
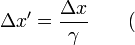 para eventos que satisfaçam
para eventos que satisfaçam 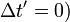
Isto mostra que o comprimento 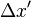 da haste tal como medido no "movimento" quadro S 'é mais curta do que o comprimento
da haste tal como medido no "movimento" quadro S 'é mais curta do que o comprimento 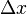 em seu próprio quadro de repouso. Este fenômeno é chamado contração do comprimento ou contração de Lorentz.
em seu próprio quadro de repouso. Este fenômeno é chamado contração do comprimento ou contração de Lorentz.
Estes efeitos não são apenas aparências; eles são explicitamente relacionado com a nossa forma de medir intervalos de tempo entre os eventos que ocorrem no mesmo lugar em um determinado sistema de coordenadas (chamado eventos "co-locais"). Estes intervalos de tempo será diferente em um outro sistema de coordenadas em movimento em relação ao primeiro, a menos que os eventos também são simultâneos. Da mesma forma, esses efeitos também se relacionam com nossas distâncias medidas entre eventos separados, mas simultâneos em um determinado sistema de coordenadas de escolha. Se estes acontecimentos não são co-local, mas estão separadas por uma distância (espaço), que não vai ocorrer à mesma distância espacial uns dos outros, quando visto a partir de um outro sistema de coordenadas em movimento.
Veja também a paradoxo dos gêmeos.
Causalidade e proibição de movimento mais rápido do que a luz

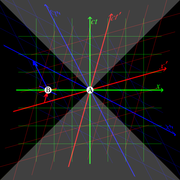
No esquema 2 do intervalo AB é "tempo-like", ou seja, há um quadro de referência no qual o evento A e B evento ocorrer no mesmo local no espaço, separadas apenas por que ocorre em tempos diferentes. Se A antecede B nesse quadro, em seguida, A precede B em todos os quadros. É hipoteticamente possível para a matéria (ou informação) para viajar de A para B, então não pode ser uma relação causal (com A e B a causa do efeito).
O AC intervalo no diagrama é 'espaço-like', ou seja, há um quadro de referência em que o evento A e C evento ocorrer simultaneamente, separados apenas no espaço. No entanto, existem também quadros em que A precede C (como mostrado) e quadros em que precede C A. Se fosse possível para de existir uma relação de causa e efeito entre os eventos A e C, em seguida, paradoxos da causalidade seria o resultado. Por exemplo, se A foi a causa e o efeito de C, então não haveria quadros de referência, em que o efeito precederam a causa. Embora isso por si só não vai dar origem a um paradoxo, pode-se mostrar que mais rápido do que sinais de luz podem ser enviadas de volta para o seu próprio passado. Um paradoxo causal pode então ser construído, enviando o sinal se e apenas se nenhum sinal foi recebido anteriormente.
Portanto, uma das consequências da relatividade especial é que (supondo causalidade deve ser preservada), nenhum objeto material ou informação pode viajar mais rápido que a luz. Por outro lado, a situação lógica não é tão clara no caso da relatividade geral, por isso é uma questão em aberto saber se existe algum princípio fundamental que preserva causalidade (e, portanto, impede o movimento mais rápido do que a luz) na relatividade geral.
Mesmo sem considerações de causalidade, existem outras fortes razões por que mais rápido do que a luz de viagens é proibido pela teoria da relatividade especial. Por exemplo, se uma força constante é aplicada a um objecto de uma quantidade ilimitada de tempo, então a integração F = dp / dt dá um impulso que cresce sem limite, mas este é simplesmente porque 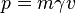 se aproxima do infinito como v se aproxima c. Para um observador que não está em aceleração, parece que a inércia do objecto está a aumentar, de modo a produzir uma aceleração mais pequena em resposta à mesma força. Este comportamento é de fato observado em aceleradores de partículas.
se aproxima do infinito como v se aproxima c. Para um observador que não está em aceleração, parece que a inércia do objecto está a aumentar, de modo a produzir uma aceleração mais pequena em resposta à mesma força. Este comportamento é de fato observado em aceleradores de partículas.
Veja também a Taquiônico Antitelephone.
Composição de velocidades
Se o observador em S vê um objeto em movimento ao longo do eixo x com velocidade w, em seguida, o observador no sistema S ', um quadro de referência em movimento em velocidade v na direção x em relação a S, vai ver o objeto em movimento com velocidade w 'onde
Esta equação pode ser derivada a partir do espaço de tempo e transformações acima. Observe que, se o objecto em movimento se a velocidade da luz no sistema de S (ou seja 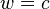 ), Então também seria mover-se à velocidade da luz no sistema de S '. Além disso, se ambos w e v são pequenos em relação à velocidade da luz, que irá recuperar a transformação de Galileu intuitiva de velocidades:
), Então também seria mover-se à velocidade da luz no sistema de S '. Além disso, se ambos w e v são pequenos em relação à velocidade da luz, que irá recuperar a transformação de Galileu intuitiva de velocidades: 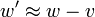 .
.
Massa, momentum e energia
Além de modificar as noções de espaço e tempo, forças especiais relatividade um para reconsiderar os conceitos de massa , dinâmica e energia , todos os quais estão construções importantes na mecânica newtoniana . Shows especiais relatividade, na verdade, que esses conceitos são todos os diferentes aspectos de uma mesma quantidade física, da mesma maneira que ele mostra o espaço eo tempo para estar inter-relacionados.
Há um par de maneiras (equivalentes) para definir momento e energia em SR. Um método utiliza leis de conservação. Se estas leis são para se mantêm válidos para SR eles devem ser verdadeiras em cada possível quadro de referência. No entanto, se um faz algumas simples pensei experimentos usando as definições de Newton de movimento e energia se vê que estas quantidades não são conservadas em SR. Pode-se resgatar a idéia de conservação, fazendo algumas pequenas modificações para as definições para explicar velocidades relativistas. São essas novas definições que são tomadas como os corretos para momento e energia em SR.
Dado um objeto de invariante massa m viajando a velocidade v a energia eo momento são dadas (e até mesmo definido) por
onde γ (a Factor de Lorentz) é dada pela
onde  é a razão entre a velocidade e a velocidade da luz. O termo γ ocorre com freqüência na relatividade, e vem da Equações de transformação de Lorentz.
é a razão entre a velocidade e a velocidade da luz. O termo γ ocorre com freqüência na relatividade, e vem da Equações de transformação de Lorentz.
Energia relativista e dinâmica pode estar relacionado com a fórmula
que é referido como a equação de energia-momento relativista. É interessante observar que, embora a energia 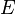 eo impulso
eo impulso 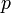 são observador dependente (variam de quadro a quadro), a quantidade
são observador dependente (variam de quadro a quadro), a quantidade 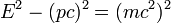 é observador independente.
é observador independente.
Para velocidades muito menores do que as da luz, γ pode ser aproximada usando uma expansão em série de Taylor e descobre-se que
Exceto o primeiro termo na expressão de energia (discutido abaixo), estas fórmulas concordam exatamente com as definições padrão de newtoniana energia cinética e momento. Isto é como deveria ser, para a relatividade especial deve concordar com a mecânica newtoniana em baixas velocidades.
Olhando para as fórmulas acima para a energia, vê-se que quando um objeto está em repouso (v = 0 e γ = 1) há um não-zero de energia remanescente:
Esta energia é a que se refere à energia como descanso. A energia restante não causa nenhum conflito com a teoria newtoniana, porque é uma constante e, tanto quanto a energia cinética está em causa, é só as diferenças de energia que sejam significativos.
Tomando esta fórmula em valor de face, vemos que na relatividade, a massa é simplesmente uma outra forma de energia. Em 1927, Einstein comentou sobre a relatividade especial:
Sob essa massa teoria não é uma magnitude inalterável, mas a magnitude dependente (e, de fato, idêntico) a quantidade de energia.
Esta fórmula se torna importante quando se mede as massas de diferentes núcleos atômicos. Ao olhar para a diferença de massas, é possível prever que os núcleos têm extra de energia armazenada que pode ser liberada por reações nucleares, fornecendo informações importantes que foi útil no desenvolvimento da energia nuclear e, consequentemente, a bomba nuclear . As implicações desta fórmula sobre a vida do século 20 tornaram uma das equações mais famosas de toda a ciência.
Massa Relativistic
Cursos de física introdutória e alguns livros didáticos mais antigos sobre a relatividade especial, por vezes, definir um massa relativista que aumenta à medida que a velocidade de um corpo aumenta. De acordo com a interpretação geométrica da relatividade especial, esta é muitas vezes preterido e o termo "massa" é reservado para significar massa invariante e é, portanto, independente do referencial inercial, ou seja, invariável.
Utilizando a definição de massa relativista, a massa de um objecto pode variar dependendo inercial do observador, da mesma forma que outras propriedades, tais como o seu comprimento pode fazê-lo. Definindo essa quantidade pode às vezes ser útil em que isso simplifica o cálculo, restringindo-o a um quadro específico. Por exemplo, considere um corpo com uma massa invariante m movendo-se em alguma velocidade em relação ao sistema de referência de um observador. Esse observador define a massa relativista de que corpo como:
"Massa Relativistic" não devem ser confundidos com os "longitudinais" e definições de "massa transversal" que foram usados por volta de 1900 e que foram baseados em uma aplicação incoerente das leis de Newton: os utilizados F = ma para uma massa variável, enquanto relativista massa corresponde à massa dinâmica de Newton em que
e
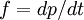 .
.
Note também que o corpo não realmente tornar-se mais maciço em seu bom quadro, uma vez que a massa relativista só é diferente para um observador em um quadro diferente. A única massa que é chassi independente é a massa invariante. Ao usar a massa relativista, o quadro de referência aplicável deve ser especificado se ele já não é óbvia ou implícita. Além disso, quase desnecessário dizer que o aumento da massa relativista não vem de um aumento do número de átomos no objecto. Em vez disso, a massa relativista de cada partícula atômica e subatômica tem aumentado.
Livros didáticos de física, por vezes, usar a massa relativista, pois permite que os alunos a utilizar os seus conhecimentos da física newtoniana para ganhar alguma compreensão intuitiva da relatividade em seu quadro de escolha (geralmente o seu próprio!). "Massa Relativistic" também é consistente com os conceitos " dilatação do tempo "e" contração de comprimento ".
Vigor
A definição clássica de ordinário força f é dada pela Segunda Lei de Newton em sua forma original:
e isto é válido em relatividade.
Muitos livros didáticos modernos reescrever a Segunda Lei de Newton como
Esta forma não é válido na relatividade ou em outras situações em que a massa M relativista está variando.
Esta fórmula pode ser substituído, no caso por relativista
Como visto a partir da equação, força e aceleração vetores comuns não são necessariamente paralelas na relatividade.
No entanto, a expressão de quatro vector que relaciona quatro vigor 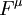 para invariante massa me quatro aceleração
para invariante massa me quatro aceleração 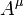 restaura a mesma forma de equação
restaura a mesma forma de equação
A geometria do espaço-tempo
SR utiliza um espaço de Minkowski 4-dimensional "plana", que é um exemplo de um espaço-tempo. Este espaço, no entanto, é muito semelhante ao padrão de 3 dimensões de espaço euclidiano , e, felizmente, por esse facto, muito fácil de trabalhar.
O diferencial da distância (ds) em espaço 3D cartesiano é definido como:
onde 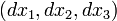 são os diferenciais das três dimensões espaciais. Na geometria da relatividade especial, uma quarta dimensão é adicionada, derivado de tempo, de modo que a equação diferencial de distância torna-se:
são os diferenciais das três dimensões espaciais. Na geometria da relatividade especial, uma quarta dimensão é adicionada, derivado de tempo, de modo que a equação diferencial de distância torna-se:
Se quiséssemos fazer o tempo coordenar olhar como coordena o espaço, podemos tratar o tempo como imaginária: x 4 = ito. Neste caso a equação acima torna-se simétrica:
Isto sugere que é de fato uma visão teórica profunda, pois mostra que a relatividade especial é simplesmente um simetria rotacional da nossa tempo-espaço, muito semelhante a simetria de rotação do espaço euclidiano . Assim como o espaço euclidiano usa um Euclidiana métrica, de modo espaço-tempo usa um Minkowski métrica. Basicamente, SR pode ser indicado em termos de invariância de intervalo de espaço-tempo (entre quaisquer dois eventos) como pode ser visto a partir de qualquer referencial inercial. Todas as equações e efeitos de relatividade especial pode ser derivado a partir desta simetria rotacional (a Grupo de Poincaré) de Minkowski espaço-tempo. De acordo com Misner (1971 §2.3), em última análise, o entendimento mais profundo da relatividade especial e geral virá a partir do estudo da métrica Minkowski (descrito abaixo) ao invés de uma "disfarçada" euclidiana métrica utilizando as TIC como o tempo de coordenadas.
Se reduzirmos as dimensões espaciais a 2, para que possamos representar a física em um espaço 3-D
Vemos que o nulo geodésicas mentir ao longo de um dual-cone:
definido pela equação
ou
Que é a equação de um círculo com r = c × dt. Se estendermos isso para três dimensões espaciais, as geodésicas nulas são o cone 4-dimensional:
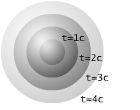
Esta dual-cone nulo representa o "linha de visão" de um ponto no espaço. Isto é, quando olhamos para as estrelas e dizer: "A luz que a estrela que eu estou recebendo é X anos de idade", nós estamos olhando para esta linha de visão: uma geodésica nula. Nós estamos olhando para um evento 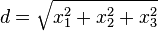 metros e d / c segundos no passado. Por esta razão, o duplo cone nulo também é conhecido como o "cone de luz". (O ponto no canto inferior esquerdo da imagem abaixo representa a estrela, a origem representa o observador, ea linha representa a "linha de visão" null geodésica.)
metros e d / c segundos no passado. Por esta razão, o duplo cone nulo também é conhecido como o "cone de luz". (O ponto no canto inferior esquerdo da imagem abaixo representa a estrela, a origem representa o observador, ea linha representa a "linha de visão" null geodésica.)
O cone na região -t é a informação de que o ponto é "receber", enquanto que o cone na secção + t é a informação de que o ponto é 'enviar'.
A geometria do espaço Minkowski pode ser representado usando Diagramas de Minkowski, que também são úteis para a compreensão muitas das experiências de pensamento na relatividade especial.
Física no espaço-tempo
Aqui, vemos como escrever as equações da relatividade especial em um manifestamente Lorentz covariantes formulário. A posição de um evento em tempo-espaço é dado por um contravariant quatro vetor cujos componentes são:
Isto é, 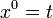 e
e 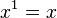 e
e 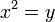 e
e 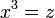 . Superscripts são índices contravariantes nesta seção, em vez de expoentes, exceto quando indicam uma praça. Subscritos são índices covariantes que também variam de zero a três como com o gradiente de um espaço-tempo φ campo:
. Superscripts são índices contravariantes nesta seção, em vez de expoentes, exceto quando indicam uma praça. Subscritos são índices covariantes que também variam de zero a três como com o gradiente de um espaço-tempo φ campo:
Metric e transformações de coordenadas
Tendo reconhecido a natureza quadridimensional do espaço-tempo, somos levados a empregar a métrica Minkowski, η, dada em componentes (válida em qualquer referencial inercial) como:
Sua recíproca é:
Então, nós reconhecemos que transformações de coordenadas entre os referenciais inerciais são dadas pelo Transformação de Lorentz tensor Λ. Para o caso especial de movimento ao longo do eixo x, temos:
que é simplesmente a matriz de um impulso (como uma rotação) entre as coordenadas x e t. Onde μ 'indica a fila e ν indica a coluna. Além disso, β e γ são definidos como:
De modo mais geral, uma transformação a partir de um referencial inercial (ignorando traduções para simplificar) para outro deve satisfazer:
onde há um somatório implícita de 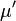 e
e 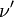 de 0 a 3 no lado da mão direita de acordo com o Convenção somatório Einstein. O Grupo de Poincaré é o grupo mais geral de transformações que preserva a Minkowski métrica e esta é a simetria física subjacente relatividade especial.
de 0 a 3 no lado da mão direita de acordo com o Convenção somatório Einstein. O Grupo de Poincaré é o grupo mais geral de transformações que preserva a Minkowski métrica e esta é a simetria física subjacente relatividade especial.
Todas as quantidades físicas adequadas são dadas por tensores. Então, para transformar a partir de um quadro para outro, usamos o bem-conhecido lei de transformação tensor
Onde 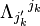 é o recíproco da matriz
é o recíproco da matriz 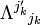 .
.
Para ver como isso é útil, vamos transformar a posição de um evento a partir de um sistema de coordenadas unprimed S a um sistema ferrado S ', calcula-
que é a transformação de Lorentz dada acima. Todos os tensores transformar pela mesma regra.
O comprimento quadrado do diferencial da posição do vector de quatro 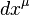 construídos usando
construídos usando
é um invariante. Sendo invariante significa que leva o mesmo valor em todos os referenciais inerciais, porque é um escalar (0 classificação tensor), e por isso não Λ aparece em sua transformação trivial. Note-se que quando o elemento de linha 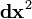 que é negativo
que é negativo 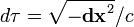 é o diferencial de tempo apropriado, enquanto que quando
é o diferencial de tempo apropriado, enquanto que quando 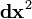 é positivo,
é positivo, 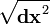 é do diferencial distância apropriada.
é do diferencial distância apropriada.
O valor primário de expressar as equações da física de forma tensor é que eles são, então, manifestamente invariante sob o grupo de Poincaré, de modo que não temos que fazer um cálculo especial e tedioso para verificar esse fato. Também na construção de tais equações nós encontramos frequentemente que as equações que se pensava estar relacionado são, de fato, intimamente ligado sendo parte da mesma equação tensor.
Velocidade e aceleração em 4D
Reconhecendo outras grandezas físicas como tensores também simplifica as suas leis de transformação. Primeira nota que a velocidade de quatro vector μ L é dada pela
Reconhecendo isso, podemos transformar a lei olhar estranho sobre a composição de velocidades em uma simples declaração sobre a transformação da velocidade de quatro vetor de uma partícula de um quadro para outro U μ também tem uma forma invariável.:
Assim, todos os quatro vetores de velocidade tem uma magnitude de c. Esta é uma expressão do fato de que não existe tal coisa como estando em coordenar resto na relatividade: pelo menos, você está sempre se movendo para a frente através do tempo. O aceleração 4-vector é dada pela 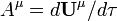 . Diante disso, diferenciando-se a equação acima por τ produz
. Diante disso, diferenciando-se a equação acima por τ produz
Assim, em relatividade, a aceleração de quatro vetor ea velocidade de quatro vetores são ortogonais.
Momentum em 4D
O momento e energia combinam em um covariante 4-vetor:
em que m é a massa invariante.
A magnitude do invariante ímpeto 4-vetor é:
Podemos trabalhar para fora o que este é invariante pela primeira argumentando que, uma vez que é um escalar, não importa qual quadro de referência que calculá-lo e, em seguida, transformando para um quadro em que o momento total é zero.
Vemos que a energia de repouso é uma invariante independente. A energia restante pode ser calculado mesmo para partículas e sistemas em movimento, traduzindo para um quadro em que o momento é zero.
A energia restante é relacionada com a massa de acordo com a equação celebrado discutido acima:
Note-se que a massa dos sistemas medidos no seu centro do quadro impulso (em que momento total é igual a zero) é determinada pela energia total do sistema neste quadro. Pode não ser igual à soma das massas individuais do sistema medidos em outros quadros.
Força em 4D
Para utilizar a terceira lei de Newton do movimento , tanto as forças deve ser definida como a taxa de variação da quantidade de movimento em relação ao mesmo tempo de coordenadas. Ou seja, ele requer a força 3D definido acima. Infelizmente, não há no tensor 4D que contém os componentes do vector de força de 3D entre os seus componentes.
Se uma partícula não está viajando em c , pode-se transformar a força 3D a partir de co-movimento referencial da partícula em referencial do observador. Isso produz um vetor de 4 chamou a quatro vigor. É a velocidade de alteração do impulso de energia acima de quatro vector em relação ao tempo adequado. A versão covariant do four-força é:
onde 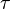 é o momento adequado.
é o momento adequado.
No quadro resto do objecto, o componente de tempo de quatro a força é igual a zero, a menos que a " massa invariante "do objecto está a mudar no caso em que é o negativo de que a taxa de tempos de troca dec 2. De um modo geral, no entanto, os componentes de quatro a força não são iguais aos componentes da força e três, porque a força de três é definida pela taxa de variação do momento com relação ao tempo de coordenadas, ou seja,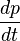 enquanto que a força de quatro é definida pela taxa de variação do momento com relação ao tempo adequado, isto é,
enquanto que a força de quatro é definida pela taxa de variação do momento com relação ao tempo adequado, isto é,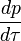 .
.
Em um meio contínuo, a 3D densidade da força combina com a densidade de potência para formar uma covariante 4-vector. A parte espacial é o resultado da divisão da força de uma pequena célula (no espaço de 3) pelo volume da célula. O componente de tempo é o negativo da potência transferida para essa célula, dividida pelo volume da célula. Este será utilizado abaixo na seção sobre eletromagnetismo.
Relatividade e eletromagnetismo unificador
A investigação teórica em electromagnetismo clássica levou à descoberta de propagação da onda. Equações generalizando os efeitos eletromagnéticos descobriu que finito velocidade de propagação dos campos E e B exigido determinados comportamentos sobre partículas carregadas. O estudo geral de cargas em movimento forma o potencial de Liénard-Wiechert, que é um passo em direção a relatividade especial.
A transformação de Lorentz do campo eléctrico de uma carga em movimento em resultados de quadro de referência de um observador que não se deslocam no aparecimento de um termo matemático comumente chamado o campo magnético. Inversamente, a magnético campo gerado por uma carga em movimento desaparece e torna-se um puramente electrostáticas campo num comóvel quadro de referência. As equações de Maxwell são, portanto, simplesmente um ajuste empírico para efeitos relativísticos especiais em um modelo clássico do Universo. Como campos elétricos e magnéticos são referencial dependente e, assim, entrelaçadas, fala-se de eletromagnéticas campos. A relatividade especial prevê as regras de transformação para a forma como um campo eletromagnético em um referencial inercial aparece em outro referencial inercial.
Eletromagnetismo em 4D
As equações de Maxwell na forma 3D já são coerentes com o conteúdo físico da relatividade especial. Mas é preciso reescrevê-los para torná-los manifestamente invariável.
O densidade de carga 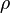 e densidade de corrente
e densidade de corrente ![[J_x,J_y,J_z] \!](../../images/531/53104.png) são unificados nacorrente de carga 4-vetor:
são unificados nacorrente de carga 4-vetor:
A lei de cobrar conservação, torna-se:
torna-se:
Ocampo elétrico ![[E_x,E_y,E_z] \!](../../images/531/53108.png) e o de indução magnética
e o de indução magnética![[B_x,B_y,B_z] \!](../../images/531/53109.png) estão agora unificadas para o (posto 2 covariant antisymmetric)tensor do campo eletromagnético:
estão agora unificadas para o (posto 2 covariant antisymmetric)tensor do campo eletromagnético:
A densidade,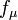 , daforça de Lorentz,
, daforça de Lorentz,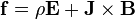 , exercida sobre a matéria pelo campo eletromagnético torna-se:
, exercida sobre a matéria pelo campo eletromagnético torna-se:
Lei de indução de Faraday, 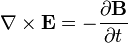 E A lei de Gauss para o magnetismo,
E A lei de Gauss para o magnetismo, 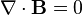 , Se combinam para formar:
, Se combinam para formar:
Embora não parecem ser de 64 equações aqui, ele realmente se reduz a apenas quatro equações independentes. Usando o antissimetria do campo eletromagnético pode-se ou reduzir a uma identidade (0 = 0) ou tornar redundantes todas as equações, exceto para aqueles com λ, μ, ν = 1,2,3 ou 2,3,0 ou 3, 0,1 ou 0,1,2.
O deslocamento elétrico![[D_x,D_y,D_z] \!](../../images/531/53117.png) e o campo magnético
e o campo magnético ![[H_x,H_y,H_z] \!](../../images/531/53118.png) estão agora unificadas para o (posto 2 contravariant antisymmetric) eletromagnética tensor deslocamento:
estão agora unificadas para o (posto 2 contravariant antisymmetric) eletromagnética tensor deslocamento:
A lei de Ampère,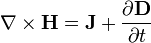 elei de Gauss,
elei de Gauss, , se combinam para formar:
, se combinam para formar:
No vácuo, asequações constitutivas são:
Antissimetria reduz esses 16 equações para apenas seis equações independentes.
O densidade de energia do campo eletromagnético combina com vetor Poynting eo estresse tensor Maxwell para formar o 4D eletromagnética tensor de tensão-energia. É o fluxo (densidade) do impulso de 4 vector e como um tensor misto posto 2 é:
onde 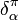 é o Kronecker delta.Quando o índice é superior reduzido com η, torna-se simétrica e é parte da fonte do campo gravitacional.
é o Kronecker delta.Quando o índice é superior reduzido com η, torna-se simétrica e é parte da fonte do campo gravitacional.
A conservação da quantidade de movimento linear e de energia pelo campo electromagnético é expressa por:
onde 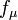 é de novo a densidade do Força de Lorentz.Esta equação pode ser deduzida a partir das equações acima (com um esforço considerável).
é de novo a densidade do Força de Lorentz.Esta equação pode ser deduzida a partir das equações acima (com um esforço considerável).
Estado
A relatividade especial é precisa apenas quando potencial gravitacional é muito menos do que c 2 ; em um campo gravitacional forte deve-se usar a relatividade geral (que se torna relatividade especial no limite do campo fraco). Em escalas muito pequenas, tais como no comprimento de Planck e abaixo, os efeitos quânticos deve ser tomado em consideração que resulta em gravidade quântica. No entanto, a escala macroscópica e na ausência de fortes campos gravitacionais, relatividade especial é testado experimentalmente para extremamente elevado grau de precisão (10 -20 ) e, portanto, aceite pela comunidade física. Resultados experimentais que parecem contradizer não são reprodutíveis e são, portanto, amplamente acreditado ser devido a erros experimentais.
Por causa da liberdade tem de se seleccionar o modo como se define unidades de comprimento e tempo na física, é possível fazer um dos dois postulados da relatividade umaconsequência tautológica das definições, mas não se pode fazer isso por tanto postula simultaneamente, como quando combinado eles têm consequências que são independentes da sua escolha de definição de comprimento e tempo.
A relatividade especial é matematicamente auto-consistente, e é uma parte orgânica de todas as teorias físicas modernas, mais notadamentea teoria quântica de campo,teoria das cordas, e da relatividade geral (no caso limite de campos gravitacionais desprezíveis).
Mecânica newtoniana segue matematicamente a partir relatividade especial às pequenas velocidades (em comparação com a velocidade da luz) - assim, a mecânica newtoniana podem ser considerados como uma relatividade especial de corpos em movimento lento. Ver Estado da relatividade especial para uma discussão mais detalhada.
Alguns experimentos-chave pode ser mencionado que levou a relatividade especial:
- O Trouton-Noble experimento mostrou que o torque em um capacitor é independente da posição e referencial inercial - tais experiências levou ao primeiro postulado
- O famoso Michelson-Morley experimento deu mais apoio ao postulado que detectar uma velocidade de referência absoluta não era viável. Refira-se aqui que, ao contrário de muitos pedidos alternativos, que disse pouco sobre a invariância da velocidade da luz no que diz respeito à fonte e velocidade do observador, tanto como fonte e observador que viajam em conjunto com a mesma velocidade em todos os momentos.
Uma série de experimentos foram realizados para testar a relatividade especial contra as teorias rivais. Estes incluem:
- Experimentos Kaufmann-Bucherer-Neumann - desvio de elétrons em concordância aproximada com previsão Lorentz-Einstein.
- Fizeau experimento - velocidade da luz em meios movendo-se em conformidade com a adição de velocidade relativista
- Kennedy-Thorndike experimento - dilatação do tempo, de acordo com transformações de Lorentz
- Rossi-Hall experimento - os efeitos relativísticos sobre meia-vida de uma partícula em movimento rápido
- As experiências para testara teoria emissor demonstraram que a velocidade da luz é independente da velocidade do emissor.
- Hammar experimento - não "obstrução do fluxo éter"
Além disso, os aceleradores de partículas rotineiramente acelerar e medir as propriedades das partículas que se deslocam a uma velocidade próxima à da luz, onde seu comportamento é completamente consistente com a teoria da relatividade e incompatível com as anteriores mecânica newtoniana . Estas máquinas simplesmente não funcionar se eles não foram projetados de acordo com princípios relativistas.

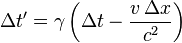
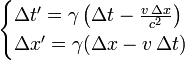
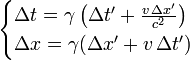
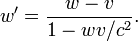
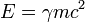
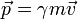
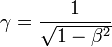
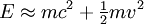
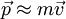
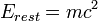
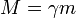
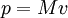
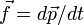

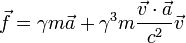
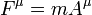
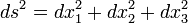
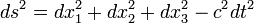
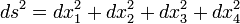
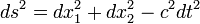

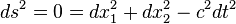
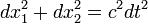
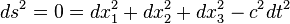
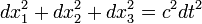
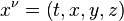

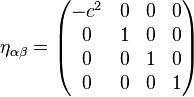
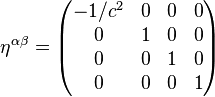
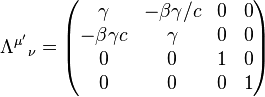
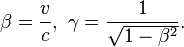
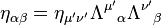
![T ^ {\ left [i_1 ', i_2', \ pontos, i_p '\ right]} _ {\ left [j_1', j_2 ', \ pontos, j_q' \ right]} = \ Lambda ^ {i_1 "} { } _ {i_1} \ Lambda ^ {i_2 '} {} _ {i_2} \ cdots \ Lambda ^ {i_p'} {} _ {i_p} \ Lambda_ {j_1 '} {} ^ {j_1} \ Lambda_ {j_2' } {} ^ {j_2} \ cdots \ Lambda_ {j_q '} {} ^ {} j_q T ^ {\ left [i_1, i_2, \ pontos, i_p \ direita]} _ {\ left [j_1, j_2, \ dots , j_q \ right]}](../../images/530/53082.png)