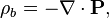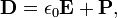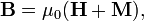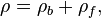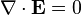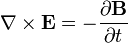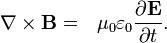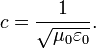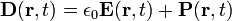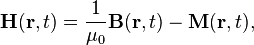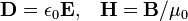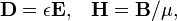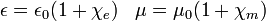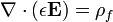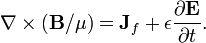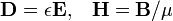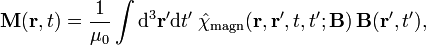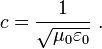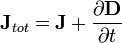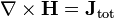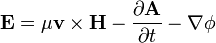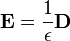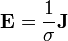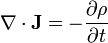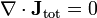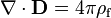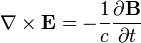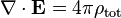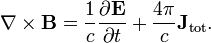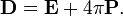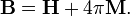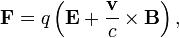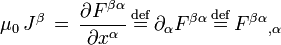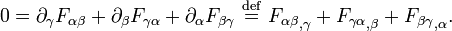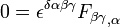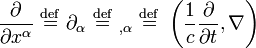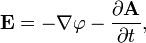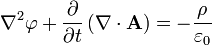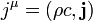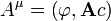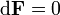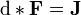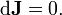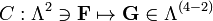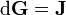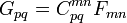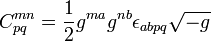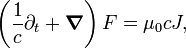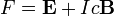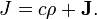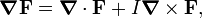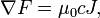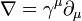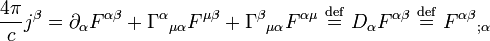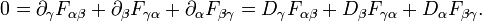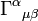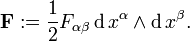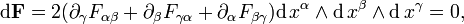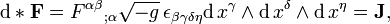As equações de Maxwell

Disciplinas relacionadas: Eletricidade e Eletrônica

Fundo para as escolas Wikipédia

Arranjar uma seleção Wikipedia para as escolas no mundo em desenvolvimento sem internet foi uma iniciativa da SOS Children. Um link rápido para o patrocínio criança é http://www.sponsor-a-child.org.uk/

Eletromagnetismo

Eletricidade Magnetismo
Eletrostática Carga elétrica Eletricidade estática Campo elétrico Condutor Insulator Triboelectricity A descarga eletrostática Indução A lei de Coulomb A lei de Gauss Fluxo elétrico / energia potencial Momento de dipolo elétrico Densidade polarização
Magnetostática A lei de Ampère Campo magnético Magnetização O fluxo magnético Lei de Biot-Savart Momento de dipolo magnético A lei de Gauss para o magnetismo
Eletrodinâmica Lei da força de Lorentz Indução eletromagnética A lei de Faraday A lei de Lenz Corrente de deslocamento As equações de Maxwell Campo eletromagnético Radiação eletromagnética Maxwell tensor Poynting vector Potencial de Liénard-Wiechert Equações de Jefimenko Eddy atual
Rede elétrica Corrente elétrica Potencial elétrico Tensão Resistência A lei de Ohm Circuito em série Circuito paralelo Corrente contínua Corrente alternada Força eletromotiva Capacidade Indutância Impedância Cavidades de ressonância Waveguides
Formulação covariante Tensor eletromagnética ( tensor de tensão-energia) Quatro atual Electromagnética de quatro potencial
Os cientistas Ampère Coulomb Faraday Gauss Heaviside Henry Hertz Lorentz Maxwell Tesla Volta Weber Ørsted

As equações de Maxwell são um conjunto de quatro equações diferenciais parciais que, em conjunto com o Lei da força de Lorentz, formam a base da eletrodinâmica clássica, clássicos óptica , e circuitos elétricos. Estes, por sua vez subjacentes à actual radioterapia, televisão-, telefone- e informação-tecnologias.

As equações de Maxwell tem duas variantes principais. O conjunto "microscópico" das equações de Maxwell usa carga total ea corrente total, incluindo os encargos nível atômico difíceis de calcular e correntes nos materiais. O conjunto "macroscópica" das equações de Maxwell define dois novos campos auxiliares que pode evitar ter que saber essas cargas e correntes 'atômicas' dimensionados.

As equações de Maxwell são nomeados em homenagem ao físico e matemático escocês James Clerk Maxwell , uma vez que eles são todos encontrados em um artigo de quatro partes, Em linhas físicas de força, que ele publicados entre 1861 e 1862. A forma matemática da lei da força de Lorentz também apareceu neste trabalho.

Muitas vezes, é útil escrever as equações de Maxwell em outras formas que são freqüentemente chamados de equações de Maxwell também. Uma formulação relativista em termos de tensores covariantes de campo é usado na relatividade especial. Enquanto, na mecânica quântica, uma versão baseada na elétrica e potenciais magnéticas é o preferido.

Descrição conceitual

Conceitualmente, as equações de Maxwell descrevem como encargos elétrica e correntes elétricas agir como fontes para os campos elétricos e magnéticos. Além disso, descreve como um tempo que varia campo eléctrico gera um campo magnético variável no tempo e vice-versa. (Veja abaixo para uma descrição matemática destas leis.) Dos quatro equações, dois deles, a lei de Gauss e A lei de Gauss para o magnetismo, descrevem como os campos emanam de encargos. (Para o campo magnético não há nenhuma carga magnética e campos magnéticos linhas, portanto, nem começar nem terminar em qualquer lugar.) As outras duas equações descrever como os campos 'circular' em torno de suas respectivas fontes; o campo magnético "circula" em torno de correntes elétricas e tempo variável campo elétrico em A lei de Ampère com a correção de Maxwell, enquanto o campo eléctrico '' circula em torno do tempo variando campos magnéticos em A lei de Faraday.

A lei de Gauss

A lei de Gauss descreve a relação entre um campo eléctrico e os geradores de cargas eléctricas : Os pontos de campo eléctrico de distância a partir de cargas positivas e cargas negativas no sentido. Na descrição linha de campo, linhas de campo elétrico começa apenas na cargas elétricas positivas e terminar apenas com cargas elétricas negativas. "Contando 'o número de linhas de campo em uma superfície fechada, por conseguinte, produz a carga total delimitada por essa superfície. Mais tecnicamente, refere-se a fluxo eléctrico através de qualquer hipotética fechadas " Superfície Gaussian "para a carga elétrica no interior da superfície.

A lei de Gauss para o magnetismo: linhas do campo magnético não começam nem voltas finais, mas de formulário ou estender ao infinito, como mostrado aqui com o campo magnético devido a um anel de corrente.

A lei de Gauss para o magnetismo

A lei de Gauss para o magnetismo afirma que não há "cargas magnéticas" (também chamados monopolos magnéticos), análogas às cargas elétricas. Em vez disso, o campo magnético devido a materiais é gerado por uma configuração de chamada dipolo. Dipolos magnéticos são mais bem representados como alças de corrente, mas assemelham-se '' cargas magnéticas positivas e negativas, inseparavelmente unidos, não tendo "carga magnética 'net. Em termos de linhas de campo, esta equação afirma que linhas de campo magnético nem começar nem fim, mas fazer voltas ou estender ao infinito e volta. Por outras palavras, qualquer linha de campo magnético que entra em um dado volume deve algures sair desse volume. Demonstrações técnicas equivalentes são que o total fluxo magnético através de toda a superfície de Gauss é zero, ou que o campo magnético é uma campo solenoidal.

A lei de Faraday

Em um tempestade geomagnética, um aumento no fluxo de partículas carregadas altera temporariamente o campo magnético da Terra, o que induz a campos elétricos na atmosfera da Terra, causando surtos em nosso elétrico redes de energia.

A lei de Faraday descreve como um tempo que varia campo magnético cria ("induz") um campo elétrico . Este aspecto indução eletromagnética é o princípio de funcionamento por trás de muitos geradores elétricos: por exemplo, uma rotação ímã de barra cria um campo magnético variável, que por sua vez gera um campo elétrico em um fio nas proximidades. (Nota: existem duas equações estreitamente relacionados que são chamados a lei de Faraday O formulário utilizado nas equações de Maxwell é sempre válido, mas mais restritiva do que originalmente formulada por. Michael Faraday .)

A lei de Ampère com a correção de Maxwell

De uma Wang a memória de núcleo magnético (1954) é uma aplicação de A lei de Ampere. Cada lojas centrais uma bit de dados.

A lei de Ampere com correcção de Maxwell afirma que os campos magnéticos podem ser gerados de duas maneiras: por corrente elétrica (este era o original "lei de Ampère") e mudando campos elétricos (esta foi "a correção de Maxwell").

Correcção de Maxwell com a lei de Ampere é particularmente importante: Isto significa que um campo magnético variável cria um campo eléctrico, um campo eléctrico e mudando cria um campo magnético. Portanto, essas equações permitir "auto-sustentáveis ondas eletromagnéticas "para viajar através do espaço vazio (veja equação de onda eletromagnética).

A velocidade calculada para ondas eletromagnéticas, que poderiam ser previstas a partir de experiências sobre cargas e correntes, corresponde exatamente à velocidade da luz ; na verdade, a luz é uma forma de radiação electromagnética (como são Raios-X, ondas de rádio, e outros). Maxwell entendeu a conexão entre as ondas eletromagnéticas e luz em 1861, unificando assim as áreas anteriormente separadas de eletromagnetismo e óptica .

Unidades e resumo das equações

As equações de Maxwell variar de acordo com o sistema de unidade usada. Embora a forma geral permanece o mesmo, várias definições se mudaram e diferentes constantes aparecer em lugares diferentes. As equações nesta secção são dadas em Unidades SI. Outras unidades são comumente utilizados Unidades de Gauss (com base no sistema CGS), Unidades de Lorentz-Heaviside (usado principalmente em física de partículas) e Unidades de Planck (usadas em física teórica). Veja abaixo para Unidades CGS-Gauss.

Para obter uma descrição da diferença entre as variantes microscópico e macroscópico das equações de Maxwell consulte as secções relevantes abaixo.

Nas equações indicadas abaixo, em negrito representam símbolos vetor quantidades, e símbolos em itálico representam quantidades escalares. As definições dos termos utilizados nas duas tabelas de equações são dadas em outra mesa imediatamente seguinte.

Tabela de equações 'microscópicas'

Formulação em termos de carga *total* e atual
Nome	Formulário diferencial	Forma integral
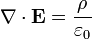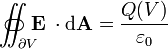A lei de Gauss	$\ Nabla \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}$	$\ Int \ \ \ \ \ \ \ \ \;!!!!!! \ \;! \ \ Subset \; \ \;! \ \ \;! \ \ \ \ \!!! \ \ \ int _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!! \; \; \; \ ! \ \ supset \ mathbf E \; \ cdot \ mathrm {d} \ mathbf A = \ frac {Q (V)} {\ varepsilon_0}$
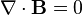A lei de Gauss para o magnetismo	$\ Nabla \ cdot \ mathbf {B} = 0$	$\ Int \ \ \ \ \ \ \ \ \;!!!!!! \ \;! \ \ Subset \; \ \;! \ \ \;! \ \ \ \ \!!! \ \ \ int _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!! \; \; \; \ ! \ \ supset \ mathbf B \; \ cdot \ mathrm {d} \ mathbf A = 0$
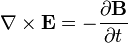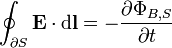Equação de Maxwell-Faraday (Lei de indução de Faraday)	$\ Nabla \ times \ mathbf {E} = - \ frac {\ \ mathbf parcial {B}} {\ partial t}$	$\ Oint _ {\ S parcial} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - \ frac {\ partial \ Phi_ {B, S}} {\ t parcial}$
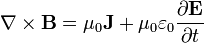Lei de Ampère (Com correção de Maxwell)	$\ Nabla \ times \ mathbf {B} = \ mu_0 \ mathbf {J} + \ mu_0 \ varepsilon_0 \ frac {\ \ mathbf parcial {E}} {\ t parcial} \$	$\ Oint _ {\ S parcial} \ mathbf {B} \ cdot \ mathrm {d} \ mathbf {l} = \ mu_0 I_S + \ mu_0 \ varepsilon_0 \ frac {\ partial \ Phi_ {E, S}} {\ t parcial }$

Tabela de equações macroscópicas ''

Formulação em termos de carga *livre* e atual
Nome	Formulário diferencial	Forma integral
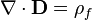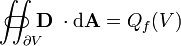A lei de Gauss	$\ Nabla \ cdot \ mathbf {D} = \ rho_f$	$\ Iint _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf D \;! \ cdot \ mathrm {d} \ mathbf A = Q_ {f} (V)$
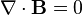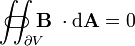A lei de Gauss para o magnetismo	$\ Nabla \ cdot \ mathbf {B} = 0$	$\ Iint _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf B \;! \ cdot \ mathrm {d} \ mathbf A = 0$
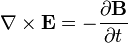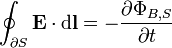Equação de Maxwell-Faraday ( Lei de indução de Faraday)	$\ Nabla \ times \ mathbf {E} = - \ frac {\ \ mathbf parcial {B}} {\ partial t}$	$\ Oint _ {\ S parcial} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - \ frac {\ partial \ Phi_ {B, S}} {\ t parcial}$
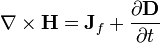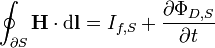Lei de Ampère (Com correção de Maxwell)	$\ Nabla \ times \ mathbf {H} = \ mathbf {J} _f + \ frac {\ \ mathbf parcial {D}} {\ partial t}$	$\ Oint _ {\ S parcial} \ mathbf {H} \ cdot \ mathrm {d} \ mathbf {l} = I_ {f, S} + \ frac {\ partial \ Phi_ {D, S}} {\ t parcial}$

Tabela de termos usados nas equações de Maxwell

A tabela a seguir fornece o significado de cada símbolo eo Unidade SI de medida:

Definições e unidades
Símbolo	Significado (primeiro termo é o mais comum)	SI Unidade de Medida
$\ Mathbf {E} \$	campo elétrico também chamado a intensidade do campo eléctrico	volt por metro ou, de forma equivalente, por newton coulomb
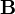$\ Mathbf {B} \$	campo magnético também chamada a indução magnética também chamado de densidade de campo magnético também chamada a densidade de fluxo magnético	tesla, ou equivalentemente, weber por metro quadrado, volt - segundo por metro quadrado
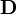$\ Mathbf {D} \$	campo deslocamento elétrico também chamado de indução eléctrica também chamada a densidade de fluxo eléctrico	coulombs por metro quadrado ou equivalente, newton por volt - medidor
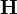$\ Mathbf {H} \$	campo de magnetização também chamado campo magnético auxiliar também chamado de intensidade de campo magnético também chamado campo magnético	ampere por medidor
$\ Mathbf {\ nabla \ cdot}$	o divergência operador	por metro (fator contribuiu através da aplicação de qualquer operador)
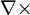$\ Mathbf {\ nabla \ times}$	a onda operador
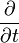$\ Frac {\ partial} {\ partial t}$	derivada parcial em relação a tempos	por segundo (fator contribuiu aplicando o operador)
$\ Mathrm {d} \ mathbf {A}$	vetor elemento diferencial de área de superfície A, com infinitamente pequena magnitude e direção normal à superfície S	metros quadrados
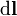$\ Mathrm {d} \ mathbf {l}$	vetor elemento diferencial de comprimento caminho tangencial para o caminho / curva	metros
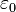$\ Varepsilon_0 \$	permissividade do espaço livre, também chamado de constante elétrica, uma constante universal	farads por metro
$\ Mu_0 \$	permeabilidade do espaço livre, também chamado o magnético constante, uma constante universal	henries por metro, ou newtons por ampere quadrado
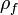$\ \ Rho_f \$	livre densidade de carga (não incluindo carga acoplado)	coulombs por metro cúbico
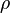$\ \ Rho \$	total densidade de carga (incluindo tanto livre e carga acoplado)	coulombs por metro cúbico
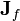$\ Mathbf {J} _f$	livre densidade de corrente (não incluindo atual ligado)	amperes por metro quadrado
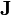$\ Mathbf {J}$	total densidade de corrente (incluindo tanto livre e atual ligado)	amperes por metro quadrado
$\, Q_f (V)$	líquido livre carga eléctrica dentro do tridimensional volume V (não incluindo carga acoplado)	coulombs
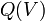$\, Q (V)$	líquido carga eléctrica dentro do tridimensional volume V (incluindo tanto livre e carga acoplado)	coulombs
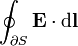$\ Oint _ {\ S parcial} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l}$	A linha integrante do campo eléctrico ao longo do ∂S contorno de uma superfície (S ∂S é sempre uma curva fechada ).	joules por coulomb
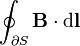$\ Oint _ {\ S parcial} \ mathbf \ cdot \ mathrm {d} {B} \ mathbf {l}$	A linha integrante do campo magnético sobre as ∂S limite fechado da superfície S	tesla metros
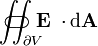$\ Iint _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf E \;! \ cdot \ mathrm {d} \ mathbf A$	o fluxo elétrico ( integrante da superfície do campo eléctrico) através do ( superfície fechada) 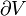$\ V parcial$ (O limite do volume V)	joule-metro por coulomb
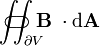$\ Iint _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf B \;! \ cdot \ mathrm {d} \ mathbf A$	o fluxo magnético ( integrante da superfície do campo magnético B-) através do ( superfície fechada) 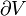$\ V parcial$ (O limite do volume V)	tesla metros ao quadrado ou webers
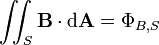$\ Iint_S \ mathbf {B} \ cdot \ mathrm {d} \ mathbf {A} = \ Phi_ {B, S}$	fluxo magnético através de toda a superfície S, não necessariamente fechado	webers ou equivalentemente, volt-segundos
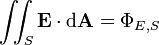$\ Iint_S \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {A} = \ Phi_ {E, S}$	fluxo elétrico através de qualquer superfície S, não necessariamente fechadas	Joule-metros por coulomb
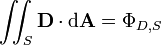$\ Iint_S \ mathbf {D} \ cdot \ mathrm {d} \ mathbf {A} = \ Phi_ {D, S}$	fluxo de campo deslocamento elétrico através de qualquer superfície S, não necessariamente fechadas	coulombs
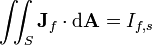$\ Iint_S \ mathbf {J} _f \ cdot \ mathrm {d} \ mathbf {A} = I_ {f, s}$	líquido livre corrente eléctrica que passa através da superfície S (não incluindo atual ligado)	amperes
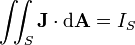$\ Iint_S \ mathbf {J} \ cdot \ mathrm {d} \ mathbf {A} = I_ {s}$	líquido passagem de corrente eléctrica através da superfície S (incluindo tanto livre e atual ligado)	amperes

A prova de que as duas formulações gerais são equivalentes

As duas formulações gerais alternativas de equações de Maxwell dados acima são matematicamente equivalentes e relacionados pelas seguintes relações:

$\ Rho_b = - \ nabla \ cdot \ mathbf {P},$

$\ Mathbf {J} _B = \ nabla \ times \ mathbf {M} + \ frac {\ \ mathbf parcial {P}} {\ t parcial},$

$\ Mathbf {D} = \ epsilon_0 \ mathbf {E} + \ mathbf {P},$

$\ Mathbf {B} = \ mu_0 (\ mathbf {H} + \ mathbf {M}),$

$\ Rho = \ rho_b + \ rho_f, \$

$\ Mathbf {J} = \ mathbf {J} _B + \ mathbf {J} _f,$

em que P e M são polarização e magnetização, e ρ _b e j _b é obrigado carga e corrente, respectivamente. Substituindo estas equações nas equações macroscópicas '' de Maxwell dá de forma idêntica as equações microscópicas.

'' Equações microscópicas de Maxwell

A variante microscópica da equação de Maxwell expressa o campo elétrico eo campo magnético B em termos de carga total e corrente presentes total, incluindo os encargos e as correntes no nível atômico. É chamado às vezes a forma geral das equações de Maxwell ou "equações de Maxwell em um vácuo". Ambas as variantes das equações de Maxwell são igualmente geral, no entanto, uma vez que são matematicamente equivalente. As equações microscópicas são mais úteis em guias de onda, por exemplo, quando não existem materiais dieléctricos ou magnéticos nas proximidades.

Formulação em termos de carga *total* e atual
Nome	Formulário diferencial	Forma integral
A lei de Gauss	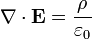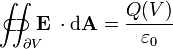$\ Nabla \ cdot \ mathbf {E} = \ frac {\ rho} {\ varepsilon_0}$	$\ Iint _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf E \;! \ cdot \ mathrm {d} \ mathbf A = \ frac {Q (V)} {\ varepsilon_0}$
A lei de Gauss para o magnetismo	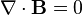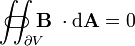$\ Nabla \ cdot \ mathbf {B} = 0$	$\ Iint _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf B \;! \ cdot \ mathrm {d} \ mathbf A = 0$
Equação de Maxwell-Faraday (Lei de indução de Faraday)	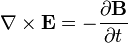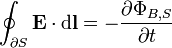$\ Nabla \ times \ mathbf {E} = - \ frac {\ \ mathbf parcial {B}} {\ partial t}$	$\ Oint _ {\ S parcial} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - \ frac {\ partial \ Phi_ {B, S}} {\ t parcial}$
Lei de Ampère (Com correção de Maxwell)	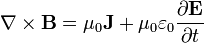$\ Nabla \ times \ mathbf {B} = \ mu_0 \ mathbf {J} + \ mu_0 \ varepsilon_0 \ frac {\ \ mathbf parcial {E}} {\ t parcial} \$	$\ Oint _ {\ S parcial} \ mathbf {B} \ cdot \ mathrm {d} \ mathbf {l} = \ mu_0 I_S + \ mu_0 \ varepsilon_0 \ frac {\ partial \ Phi_ {E, S}} {\ t parcial }$

Com nem acusações nem correntes

Em uma região sem custos ρ (= 0) e não há correntes (j = 0), tal como num vácuo, as equações de Maxwell reduzir a:

$\ Nabla \ cdot \ mathbf {E} = 0$

$\ Nabla \ cdot \ mathbf {B} = 0$

$\ Nabla \ times \ mathbf {E} = - \ frac {\ \ mathbf parcial {B}} {\ partial t}$

$\ Nabla \ times \ mathbf {B} = \ \ \ mu_0 \ varepsilon_0 \ frac {\ \ mathbf parcial {E}} {\ partial t}.$

Estas equações conduzem directamente a E e B satisfazem a equação de onda para os quais as soluções são combinações lineares de ondas planas que viajam na velocidade da luz ,

$c = \ frac {1} {\ sqrt {\ mu_0 \ varepsilon_0}}. \$

Além disso, E e B são mutuamente perpendiculares entre si e à direcção do movimento e estão em fase uns com os outros. A onda sinusoidal avião é uma solução especial destas equações.

Na verdade, as equações de Maxwell explicar como essas ondas podem propagar fisicamente através do espaço. O campo magnético variável cria um campo elétrico variável através A lei de Faraday. Por sua vez, que o campo eléctrico cria um campo magnético variável através A correção de Maxwell à lei de Ampère. Este ciclo perpétuo permite que essas ondas, agora conhecido como radiação eletromagnética , para se mover pelo espaço a uma velocidade c.

'' Equações macroscópicas de Maxwell

Ao contrário das equações microscópicas '', "equações de Maxwell macroscópicos", também conhecidas como equações de Maxwell em questão, fatorar a carga amarrado e atual para obter equações que dependem apenas as cargas livres e correntes. Essas equações são mais semelhantes aos que o próprio Maxwell introduziu. O custo deste fatoração é que os campos adicionais precisam ser definidas: a campo de deslocamento D, que é definida em termos do campo eléctrico E eo P polarização do material, e o campo magnetic- H, a qual é definida em termos do campo B e o magnetic- H magnetização do material.

Carga e corrente limite

Esquerda: Uma visão esquemática de como um conjunto de dipolos microscópicos produz cargas superficiais opostas como mostrado na parte superior e na parte inferior direita:. Como um conjunto de circuitos de corrente microscópicas adicionar em conjunto para produzir um circuito de corrente macroscopicamente circulação. Dentro dos limites, as contribuições individuais tendem a cancelar, mas nos limites nenhum cancelamento ocorre.

Quando um campo eléctrico é aplicado a um material dieléctrico suas moléculas responder através da formação de microscópico dipolos eléctricos-seus núcleos atómicos mover uma pequena distância na direcção do campo, enquanto que os seus electrões mover uma pequena distância em sentido oposto. Isso produz uma carga limite macroscópico no material, mesmo que todos os encargos envolvidos são obrigados a moléculas individuais. Por exemplo, se cada uma das moléculas responde ao mesmo, semelhante ao mostrado na figura, estes pequenos movimentos de carga se combinam para produzir uma camada de positiva carga ligado de um lado do material e uma camada de carga negativa no outro lado. A carga ligado é mais convenientemente descrito em termos de um polarização, P, no material. Se P é uniforme, uma separação macroscópica da carga é produzido apenas nas superfícies onde P entram e saem do material. Para a P não uniforme, uma carga também é produzido em grandes quantidades a.

Um tanto semelhante, em todos os materiais da exposição átomos constituintes momentos magnéticos que estão intrinsecamente ligadas ao momento angular dos componentes dos átomos, mais notavelmente seus elétrons. O conexão com o momento angular sugere a imagem de um conjunto de circuitos de corrente microscópicas. Do lado de fora do material, um conjunto de tais circuitos de corrente microscópicas não é diferente de uma corrente que circula em torno macroscópica superfície do material, apesar do facto de nenhum momento magnético indivíduo está viajando uma grande distância. Estes correntes ligadas pode ser descrito utilizando a H magnetização.

O muito complicado e granulares vinculado cargas e correntes ligadas, portanto, pode ser representado na escala macroscópica em termos de P e M, que a média desses encargos e correntes em uma escala suficientemente grande para não ver a granularidade de átomos individuais, mas também suficientemente pequenas que variam com a localização no material. Como tal, as equações de Maxwell macroscópicas ignora muitos detalhes em uma escala fina que pode ser importante para a compreensão de questões em uma escala mais grosseira por meio do cálculo campos que são em média sobre algum volume de tamanho adequado.

Equações

Formulação em termos de carga *livre* e atual
Nome	Formulário diferencial	Forma integral
A lei de Gauss	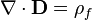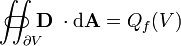$\ Nabla \ cdot \ mathbf {D} = \ rho_f$	$\ Iint _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf D \;! \ cdot \ mathrm {d} \ mathbf A = Q_ {f} (V)$
A lei de Gauss para o magnetismo	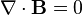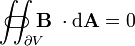$\ Nabla \ cdot \ mathbf {B} = 0$	$\ Iint _ {\ V parcial} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;!!!!!!!!!!!!!!!!! \; \ ; \ subset \ \ supset \ mathbf B \;! \ cdot \ mathrm {d} \ mathbf A = 0$
Equação de Maxwell-Faraday ( Lei de indução de Faraday)	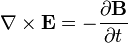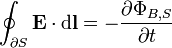$\ Nabla \ times \ mathbf {E} = - \ frac {\ \ mathbf parcial {B}} {\ partial t}$	$\ Oint _ {\ S parcial} \ mathbf {E} \ cdot \ mathrm {d} \ mathbf {l} = - \ frac {\ partial \ Phi_ {B, S}} {\ t parcial}$
Lei de Ampère (Com correção de Maxwell)	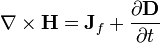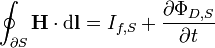$\ Nabla \ times \ mathbf {H} = \ mathbf {J} _f + \ frac {\ \ mathbf parcial {D}} {\ partial t}$	$\ Oint _ {\ S parcial} \ mathbf {H} \ cdot \ mathrm {d} \ mathbf {l} = I_ {f, S} + \ frac {\ partial \ Phi_ {D, S}} {\ t parcial}$

Relações constitutivas

A fim de aplicar as equações de Maxwell macroscópicos ", é necessário especificar as relações entre campo de deslocamento D e E, eo H-campo magnético H e B. Essas equações especificar a resposta de carga e corrente ligada aos campos aplicados e são chamados relações constitutivas.

Determinação da relação constitutiva entre os campos auxiliares D e H e dos campos E e B começa com a determinação dos próprios campos auxiliares:

$\ Mathbf {D} (\ mathbf {r}, t) = \ epsilon_0 \ mathbf {E} (\ mathbf {r}, t) + \ mathbf {P} (\ mathbf {r}, t)$

$\ Mathbf {H} (\ mathbf {r}, t) = \ frac {1} {\ mu_0} \ mathbf {B} (\ mathbf {r}, t) - \ mathbf {H} (\ mathbf {r} , t),$

onde P é a campo de polarização e M é a campo de magnetização que são definidos em termos de microscópicos vinculado encargos e atual ligado respectivamente. Antes de entrar para a forma de calcular M e P é útil para examinar alguns casos especiais, no entanto.

Sem materiais magnéticos ou dielétricos

Na ausência de materiais magnéticos ou dieléctricos, as relações constitutivas são simples:

$\ Mathbf {D} = \ epsilon_0 \ mathbf {E}, \; \; \; \ Mathbf {H} = \ mathbf {B} / \ mu_0$

onde ε ₀ e μ ₀ são duas constantes universais, o chamado permissividade do espaço livre e permeabilidade do espaço livre, respectivamente. Substituindo-los de volta em equações macroscópicas de Maxwell levam diretamente às equações microscópicas de Maxwell, exceto que as correntes e os encargos são substituídas por correntes livres e cargas livres. Isto é esperado uma vez que não há encargos vinculados nem correntes.

Materiais lineares isotrópicos

Num ( isotrópico) o material linear, em que P é proporcional a E e M é proporcional a B as relações constitutivas são também simples. Em termos de polarizaton P e a magnetização M são:

$\ Mathbf {P} = \ epsilon_0 \ chi_e \ mathbf {E}, \; \; \; \ Mathbf {M} = \ chi_m \ mathbf {H},$

onde χ _e e _m são o χ elétrica e susceptibilidades magnéticas de um dado material, respectivamente. Em termos de D e H são as relações constitutivas:

$\ Mathbf {D} = \ epsilon \ mathbf {E}, \; \; \; \ Mathbf {H} = \ mathbf {B} / \ mu,$

onde ε e μ são constantes (que depende do material), o chamado permissividade e permeabilidade, respectivamente, do material. Estes estão relacionados com as susceptibilidades por:

$\ Epsilon = \ epsilon_0 (1+ \ chi_e) \; \; \; \ Mu = \ mu_0 (1+ \ chi_m)$

Substituindo nas relações constitutivas acima em equações de Maxwell em lineares, dispersionless, materiais invariantes no tempo (única forma diferencial) são:

$\ Nabla \ cdot (\ epsilon \ mathbf {E}) = \ rho_f$

$\ Nabla \ cdot \ mathbf {B} = 0$

$\ Nabla \ times \ mathbf {E} = - \ frac {\ \ mathbf parcial {B}} {\ partial t}$

$\ nabla \ times (\ mathbf {B} / \ mu) = \ mathbf {J} _f + \ epsilon \ frac {\ \ mathbf parcial {E}} {\ partial t}.$

Estes são formalmente idêntica à formulação geral em termos de E e B (dado acima), excepto que o permissividade do espaço livre foi substituído com o permitividade do material, o permeabilidade do espaço livre foi substituído com o permeabilidade do material, e apenas cargas livres e correntes estão incluídos (em vez de todas as cargas e correntes). A não ser que o material é homogênea no espaço, ε e μ não pode ser tomada fora das expressões derivados sobre os lados esquerdo.

Caso geral

Para materiais do mundo real, as relações constitutivas não são lineares, exceto aproximadamente. Calculando as relações constitutivas de primeiros princípios envolve determinar como P e M são criados a partir de um dado E e B. Essas relações podem ser empíricas (com base em medições diretamente), ou teórico (com base na mecânica estatística , teoria de transporte ou outras ferramentas de física da matéria condensada ). O detalhe empregue pode ser macroscópica ou microscópico, dependendo do nível necessário ao problema sob escrutínio.

Em geral, porém as relações constitutivas normalmente pode ainda ser escrita:

$\ Mathbf {D} = \ epsilon \ mathbf {E}, \; \; \; \ Mathbf {H} = \ mathbf {B} / \ mu$

mas ε e μ não são, em geral, as constantes simples, mas sim funções. Exemplos são:

Dispersão e absorção onde ε e μ são funções de frequência. (A causalidade não permite que os materiais a ser não dispersivo; ver, por exemplo, Kramers-Kronig relações). Nem os campos precisam estar na fase que leva a ser ε e μ complexo . Isto também leva a absorção.
Bi- (a) isotropia em que H e D dependem tanto B e E:

$D = \ epsilon E + \ xi H \; \; \; B = \ mu H + \ zeta E.$

Não-linearidade, onde ε e μ são funções de E e B.
Anisotropy (como birefringence ou dicroï¿½mo) que ocorre quando ε e μ são de segunda ordem tensores,

$D_j = \ epsilon_ {ij} E_i \; \; \; B_j = \ mu_ {ij} H_i.$

Dependência de P e M em E e B em outros locais e horários. Isto pode ser devido à falta de homogeneidade espacial; por exemplo, numa estrutura domained, heteroestrutura ou um cristal líquido , ou mais geralmente na situação em que não são simplesmente múltiplos materiais que ocupam diferentes regiões de espaço). Ou poderia ser devido a um meio variável no tempo ou devido a histerese. Em tais casos P e M pode ser calculada como:

$\ Mathbf {P} (\ mathbf {r}, t) = \ epsilon_0 \ int {\ rm d} ^ 3 \ mathbf {r} '{\ rm d} t' \; \ Hat {\ chi} _ {\ mathrm {elec}} (\ mathbf {r}, \ mathbf {r} ', t, t'; \ mathbf {E}) \, \ mathbf {E} (\ mathbf { r} ', t')$

$\ Mathbf {H} (\ mathbf {r}, t) = \ frac {1} {\ mu_0} \ int {\ rm d} ^ 3 \ mathbf {r} '{\ rm d} t' \; \ Hat {\ chi} _ {\ mathrm {magn}} (\ mathbf {r}, \ mathbf {r} ', t, t'; \ mathbf {B}) \, \ mathbf {B} (\ mathbf { r} ', t'),$

em que as funções de permitividade e de permeabilidade são substituídos por integrais ao longo do mais geral elétrica e susceptibilidades magnéticas.

Na prática, algumas propriedades dos materiais tem um impacto insignificante em circunstâncias particulares, permitindo negligência de pequenos efeitos. Por exemplo: não linearidades ópticas podem ser negligenciadas por fortes baixas de campo; dispersão de material não é importante quando a frequência está limitada a um estreito largura de banda; material de absorção pode ser negligenciada para comprimentos de onda para a qual o material é transparente; e metais com condutividade finito, muitas vezes são aproximadas à microondas ou comprimentos de onda mais longos como metais perfeitos com infinita condutividade (formando barreiras rígidos com zero de profundidade da pele de penetração de campo).

Pode notar-se que os materiais feitos pelo homem pode ser concebido para ter permissividade personalizado e permeabilidade, tal como metamateriais e cristais fotônicos.

Cálculo das relações constitutivas

Em geral, as equações constitutivas são teoricamente determinada pelo cálculo como uma molécula responde aos campos locais através da Força de Lorentz. Outras forças podem precisar de ser modelado, bem como vibrações da estrutura em forma de cristais ou forças de obrigações. Incluindo todas as forças leva a alterações na molécula os quais são utilizados para calcular P e M como uma função dos campos locais.

Os campos locais diferentes dos campos aplicados devido aos campos produzidos pela polarização e de magnetização do material nas proximidades; um efeito que também precisa de ser modelado. Além disso, não são materiais reais mídia contínua; os campos locais de materiais reais variam muito na escala atômica. Os campos devem ser calculados sobre um volume adequado para formar uma aproximação continuum.

Estas aproximações do contínuo muitas vezes exigem algum tipo de mecânica quântica análise tais como teoria quântica de campos como aplicado a física da matéria condensada . Ver, por exemplo, teoria do funcional da densidade, Relações verde-Kubo e Função de Green. Vários equações de transporte aproximados evoluíram, por exemplo, a Ou a equação de Boltzmann Equação de Fokker-Planck ou o Equações de Navier-Stokes. Alguns exemplos onde estas equações são aplicados são magnetohydrodynamics, dinâmica dos fluidos, electro, supercondutividade , modelação do plasma. Todo um aparato físico para lidar com estas questões se desenvolveu. Um conjunto diferente de métodos de homogeneização (evoluindo de uma tradição em materiais de tratamento, tais como conglomerados e laminados) são baseados na aproximação de um material não homogéneo por um homogénea meio eficaz (válido para excitações com comprimentos de onda muito maior do que a escala da falta de homogeneidade).

A modelagem teórica das propriedades continuum de aproximação de muitos materiais reais muitas vezes dependem de medição, bem como, por exemplo, medições elipsometria.

História

Relação entre a electricidade, magnetismo, e a velocidade da luz

A relação entre a electricidade, magnetismo, e a velocidade da luz pode ser resumido pela equação moderna:

$c = \ frac {1} {\ sqrt {\ mu_0 \ varepsilon_0}} \.$

O lado esquerdo é a velocidade da luz, e do lado direito é uma quantidade relacionada com as equações que regem a eletricidade eo magnetismo. Embora o lado direito tem unidades de velocidade, pode-se inferir a partir de medições de forças elétricas e magnéticas, que não envolvam velocidades físicas. Portanto, estabelecer essa relação forneceram evidências convincentes de que a luz é um fenômeno eletromagnético.

A descoberta desse relacionamento começou em 1855, quando Wilhelm Eduard Weber e Rudolf Kohlrausch determinou que havia uma quantidade relacionada com a electricidade e magnetismo, "a relação entre a unidade electromagnética absoluta da carga para a unidade de carga electrostática absoluto" (em linguagem moderna, o valor 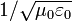$1 / \ sqrt {\ mu_0 varepsilon_0 \}$ ), E determinado que ele deve ter unidades de velocidade. Eles, então, medida esta relação por um experimento que envolveu um carregamento e descarregamento Garrafa de Leyden e medir a força magnética da corrente de descarga, e encontrou um valor de 3,107 × 10 ⁸ m / s, notavelmente perto da velocidade da luz, que havia sido recentemente medidos a 3,14 x 10 ⁸ m / s por Hippolyte Fizeau em 1848 e em 2,98 × 10 ⁸ m / s por Léon Foucault em 1850. No entanto, Weber e Kohlrausch não fazer a conexão com a velocidade da luz. Para o fim de 1861, enquanto trabalhava em parte III do seu papel Em linhas físicas de força, Maxwell explorada da Escócia para Londres e olhou para cima Weber e os resultados do Kohlrausch. Ele converteu-os em um formato que era compatível com seus próprios escritos, e ao fazer isso ele estabeleceu a conexão com a velocidade da luz e concluiu que a luz é uma forma de radiação eletromagnética.

Equações de Maxwell O termo

As quatro equações de Maxwell modernos pode ser encontrada individualmente ao longo de seu artigo 1861, derivada teoricamente utilizando um modelo de vórtice molecular de Michael Faraday 's "linhas de força" e em conjunto com o resultado experimental de Weber e Kohlrausch. Mas não foi até 1884 que Oliver Heaviside, simultaneamente com um trabalho semelhante por Willard Gibbs e Heinrich Hertz, agrupados os quatro juntos em um conjunto distinto. Este grupo de quatro equações foi conhecida também como as equações Hertz-Heaviside e as equações de Maxwell-Hertz, e às vezes são ainda conhecidas como as equações de Maxwell-Heaviside.

A contribuição de Maxwell para a ciência na produção destas equações reside na correção que ele fez para Lei de Ampère em seu artigo de 1861 Em linhas físicas de força. Ele acrescentou que a deslocamento atual mandato de Lei de Ampère e isso permitiu-lhe obter a equação da onda eletromagnética em sua posterior 1865 papel A Teoria Dinâmica do Campo Eletromagnético e demonstrar o fato de que a luz é uma onda eletromagnética . Este facto foi, em seguida, mais tarde confirmado experimentalmente por Heinrich Hertz em 1887. O físico Richard Feynman previu que, "A Guerra Civil Americana vai pálida insignificância provincial em comparação com este importante evento científico da mesma década."

. O conceito de campos foi introduzido por, entre outros, Faraday Albert Einstein escreveu:

A formulação exacta das leis do espaço-tempo foi o trabalho de Maxwell. Imagine que seus sentimentos quando as equações diferenciais que ele tinha formulado mostrou-lhe que os campos eletromagnéticos distribuídos sob a forma de ondas polarizadas, e na velocidade da luz! Para alguns homens no mundo tem tal experiência foi concedida ... que levou os físicos algumas décadas para compreender o significado completo da descoberta de Maxwell, tão ousada foi o salto que seu gênio forçada sobre as concepções de seus companheiros de trabalho
- (Science, 24 de maio de 1940)

Heaviside trabalhado para eliminar os potenciais ( potencial eléctrico e potencial magnético) que Maxwell tinha usado como os conceitos centrais em suas equações; este esforço foi um pouco controversa, apesar de ter sido entendido por 1884 que os potenciais deve propagar na velocidade da luz como os campos, ao contrário do conceito de ação instantânea-em-um-distância, como o então concepção de potencial gravitacional. Análise moderna de, por exemplo, antenas de rádio, faz pleno uso de vetores e escalares potenciais de Maxwell para separar as variáveis, uma técnica comum usada na formulação das soluções de equações diferenciais. No entanto, os potenciais podem ser introduzidas por manipulação algébrica das quatro equações fundamentais.

Em linhas físicas de Força

As quatro equações de Maxwell dias modernos apareceram durante todo 1861 papel de Maxwell nas linhas físicas de força:

A equação (56), em 1861, papel de Maxwell é ∇ ⋅ B = 0.
Equação (112) está Lei de Ampère com corrente de deslocamento de Maxwell acrescentou. É a adição de corrente de deslocamento que é o aspecto mais importante do trabalho de Maxwell no eletromagnetismo , pois permitiu-lhe mais tarde a derivar equação da onda eletromagnética em seu papel 1865 A Teoria Dinâmica do Campo Eletromagnético, e, portanto, mostrar que a luz é uma onda eletromagnética. É, portanto, este aspecto da obra de Maxwell que dá as equações pleno significado. (Curiosamente, o derivado Kirchhoff equações de telegrafista em 1857 sem usar corrente de deslocamento. Mas ele usou a equação de Poisson ea equação de continuidade que são os ingredientes matemáticas do corrente de deslocamento. No entanto, acredita Kirchhoff suas equações de ser aplicável apenas no interior de um fio elétrico e para que ele não é creditado por ter descoberto que a luz é uma onda eletromagnética).
A equação (115) é a lei de Gauss .
A equação (54) é uma equação que Oliver Heaviside denominada «lei de Faraday '. Esta equação serve para o tempo que varia aspecto da indução eletromagnética, mas não para o aspecto motionally induzida, que o direito de fluxo original de Faraday atende a ambos os aspectos. Maxwell lida com o aspecto motionally dependente da indução eletromagnética, v × B , a equação (77). A equação (77), que é o mesmo que a equação (D) nos oito equações de Maxwell originais listados abaixo, corresponde a todos os efeitos para a lei da força moderna F = q ( E + V × B ), que fica ao lado equações de Maxwell e leva o nome Lorentz vigor, apesar de Maxwell derivada quando Lorentz ainda era um jovem garoto.

A diferença entre oBe osHvetores pode ser rastreada até 1855 papel de Maxwell direitoem linhas de força de Faradayque foi lido para o Cambridge Philosophical Society. O artigo apresentou um modelo simplificado da obra de Faraday, e como os dois fenômenos foram relacionados.Reduziu todo o conhecimento atual em um conjunto articulado deequações diferenciais.

Figura de modelo vortex molecular de Maxwell. Para um campo magnético uniforme, as linhas de campo apontam para fora a partir do ecrã de visualização, como pode ser observado a partir dos pontos pretos no meio dos hexágonos. O vórtice de cada molécula hexagonal gira no sentido anti-horário. Os pequenos círculos verdes estão girando no sentido horário partículas imprensando entre os vórtices moleculares.

Mais tarde é esclarecido em seu conceito de um mar de vórtices moleculares que aparece em seu papel 1861 Em linhas físicas de força. Dentro desse contexto, H representado vorticidade puro (spin), enquanto que B era uma vorticidade ponderada que foi ponderado para a densidade do mar vortex. Maxwell considerado permeabilidade magnética μ ser uma medida da densidade do mar vórtice. Por conseguinte, a relação,

Corrente de indução magnéticaprovoca uma densidade de corrente magnética
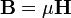
$\mathbf{B} = \mu \mathbf{H}$
era essencialmente uma analogia de rotação para a relação linear de corrente eléctrica,
Corrente de convecção elétrico
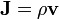
$\mathbf{J} = \rho \mathbf{v}$

onde ρ é a densidade de carga eléctrica. B era visto como uma espécie de corrente magnética de vórtices alinhados nos seus planos axiais, com H sendo a velocidade circunferencial dos vórtices. Com μ representando densidade vórtice, segue-se que o produto de μ com vorticidade H leva ao campo magnético indicado como B .

A equação de corrente eléctrica pode ser visto como uma corrente convectiva de carga eléctrica que envolve o movimento linear. Por analogia, a equação magnética é uma corrente indutiva envolvendo rodada. Não existe movimento linear na corrente indutiva ao longo da direcção do B vetor. A corrente indutiva magnética representa linhas de força. Em particular, ela representa linhas de força inversa quadrática.

A extensão das considerações acima expostas confirma que onde B é H , e onde J é a ρ , em seguida, segue-se necessariamente da lei de Gauss e da equação da continuidade da acusação de que E é D . ie B paralelos com E , enquanto H paralelos com D .

A Teoria Dinâmica do Campo Eletromagnético

Em 1864 Maxwell publicou A Teoria Dinâmica do Campo Eletromagnético em que ele mostrou que a luz era um fenômeno eletromagnético. A confusão sobre o termo "equações de Maxwell" é agravado porque ele também é usado às vezes por um conjunto de oito equações que apareceram na Parte III de 1864 papel de Maxwell A Teoria Dinâmica do Campo Eletromagnético, intitulado a "Equações gerais do campo eletromagnético," confusão agravada pela escrita de seis dos oito dessas equações como três equações separadas (uma para cada um dos eixos cartesianos), resultando em vinte e vinte equações incógnitas. (Como notado acima, esta terminologia não é comum: modernos referências ao termo "equações de Maxwell" referem-se as reformulações Heaviside).

Os oito equações de Maxwell originais podem ser escritos em notação vectorial moderno como se segue:

(A) A lei das correntes totais

$\mathbf{J}_{tot} = \mathbf{J} + \frac{\partial\mathbf{D}}{\partial t}$

(B) A equação da força magnética

$\mu \mathbf{H} = \nabla \times \mathbf{A}$

Lei circuital (C) de Ampère

$\nabla \times \mathbf{H} = \mathbf{J}_\mathrm{tot}$

Vigor (D) Electromotive criado por convecção, a indução, e pela eletricidade estática. (Isto é, com efeito a força de Lorentz)

$\mathbf{E} = \mu \mathbf{v} \times \mathbf{H} - \frac{\partial\mathbf{A}}{\partial t}-\nabla \phi$

(E) A equação elasticidade elétrica

$\mathbf{E} = \frac{1}{\epsilon} \mathbf{D}$

Direito (F) de Ohm

$\mathbf{E} = \frac{1}{\sigma} \mathbf{J}$

Direito (G) de Gauss

$\nabla \cdot \mathbf{D} = \rho$

(H) A equação de continuidade

$\nabla \cdot \mathbf{J} = -\frac{\partial\rho}{\partial t}$

$\nabla \cdot \mathbf{J}_\mathrm{tot} = 0$

Notação: Hé ocampo de magnetização, que Maxwell chamado deintensidade magnética.; Jé adensidade de corrente (comJ _copinhosendo a corrente total incluindo corrente de deslocamento).; D é a campo de deslocamento (chamado dedeslocamento elétricopor Maxwell).; ρé adensidade de carga livre (chamado dequantidade de eletricidade livrede Maxwell).; Umé opotencial magnético (chamado aimpulsão angularpor Maxwell).; Eé chamado deforça eletromotrizpor Maxwell. O termo força eletromotriz é usada hoje em dia para a tensão, mas é claro a partir do contexto de que o significado de Maxwell correspondia mais ao termo modernocampo elétrico.; φé opotencial elétrico (que Maxwell também chamado depotencial elétrico).; σé acondutividade elétrica (Maxwell chamado o inverso da condutividade aresistência específica, o que hoje é chamado deresistividade).

É interessante notar oμ v×Htermo que aparece em D. equação Equação D é, por conseguinte, de forma eficaz aforça de Lorentz, de forma semelhante à equação (77) do seu papel de 1861 (ver acima).

Quando Maxwell deriva a equação da onda eletromagnética em seu artigo de 1865, ele usa equação D para atender a indução eletromagnética, em vez de lei de indução de Faraday, que é usado em livros didáticos modernos. (Lei de Faraday em si não aparece entre suas equações.) No entanto, Maxwell cai o μ v × H termo da equação D quando ele é derivar a equação de onda eletromagnética, como ele considera a situação apenas a partir do referencial de repouso.

Um Tratado sobre Eletricidade e Magnetismo

Em Um Tratado sobre Eletricidade e Magnetismo, uma 1,873tratado sobreeletromagnetismoescrito porJames Clerk Maxwell, onze equações gerais do campo eletromagnético são listados e estas incluem os oito que são listadas no artigo 1865.

Equações de Maxwell e relatividade

Equações originais de Maxwell são baseadas na idéia de que a luz viaja através de um mar de vórtices moleculares conhecidas como o " éter luminífero ", e que a velocidade da luz tem que ser ao respectivo quadro de referência deste éter. Medidas destinadas a medir a velocidade da Terra através do éter em conflito, no entanto.

Uma abordagem mais teórica foi sugerido por Hendrik Lorentz, juntamente com George FitzGerald e Joseph Larmor. Ambos Larmor (1897) e Lorentz (1899, 1904) derivada da transformação de Lorentz (assim chamado por Henri Poincaré) como aquela sob a qual as equações de Maxwell foram invariável. Poincaré (1900) analisaram a coordenação do movimento relógios através da troca de sinais de luz. Ele também estabeleceu matematicamente a propriedade de grupos da transformação de Lorentz (Poincaré 1905).

Einstein negou provimento ao éter como desnecessária e concluiu que as equações de Maxwell prever a existência de uma velocidade fixa de luz, independente da velocidade do observador, e como tal ele usou equações de Maxwell como o ponto de partida de sua teoria da relatividade especial . Ao fazer isso, ele estabeleceu a transformação de Lorentz como documento válido para toda a matéria e não apenas as equações de Maxwell. As equações de Maxwell desempenhou um papel fundamental no famoso artigo de Einstein sobre a relatividade especial; por exemplo, no número do papel de abertura, que motivou a sua teoria, notando que uma descrição de um condutor que se move em relação a um íman deve gerar um conjunto consistente de campos independentemente do facto de a força é calculado no quadro resto do magneto ou que a do condutor.

Geral relatividade também teve uma relação estreita com as equações de Maxwell. Por exemplo, Theodor Kaluza e Oskar Klein mostrou em 1920 que as equações de Maxwell podem ser derivadas ao se estender a relatividade geral em cinco dimensões. Essa estratégia de se usar dimensões maiores para unificar diferentes forças continua sendo uma área ativa de pesquisa em física de partículas .

Modificada para incluir monopolos magnéticos

Equações do eletromagnetismo de Maxwell relacionar os campos elétricos e magnéticos para os movimentos de cargas elétricas. A forma padrão das equações de prever uma carga elétrica, mas postulam nenhuma carga magnética. Não há analógica magnético conhecido de um elétron, no entanto, recentemente os cientistas têm descrito comportamento em um estado cristalino de matéria conhecido como spin-gelo, que têm comportamento macroscópico como monopolos magnéticos. (Em conformidade com o facto de carga magnética foi visto e pode não existir). Exceto por isso, as equações são simétricas com respeito ao intercâmbio de campo elétrico e magnético. Na verdade, as equações simétricas pode ser escrito quando todas as acusações são zero, e é assim que a equação de onda é derivado (ver imediatamente acima).

Totalmente equações simétrica também pode ser escrito se uma permite a possibilidade de cargas magnéticas. Com a inclusão de uma variável para estas cargas magnéticas, dizer ρ _m , haverá também uma variável "magnético actual" nas equações, J _m . As equações de Maxwell (estendidos em unidades CGS-Gaussiana) são os seguintes:

Nome	Sem monopolos magnéticos	Com monopolos magnéticos (hipotético)
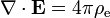
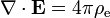
A lei de Gauss:	$\nabla \cdot \mathbf{E} = 4 \pi \rho_\mathrm{e}$	$\nabla \cdot \mathbf{E} = 4 \pi \rho_\mathrm{e}$
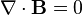
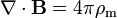
A lei de Gauss para o magnetismo:	$\ Nabla \ cdot \ mathbf {B} = 0$	$\nabla \cdot \mathbf{B} = 4 \pi \rho_\mathrm{m}$
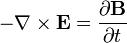
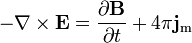
Equação de Maxwell-Faraday ( Lei de indução de Faraday):	$-\nabla \times \mathbf{E} = \frac{\partial \mathbf{B}} {\partial t}$	$-\nabla \times \mathbf{E} = \frac{\partial \mathbf{B}}{\partial t} + 4 \pi \mathbf{j}_\mathrm{m}$
A lei de Ampère (Com extensão de Maxwell):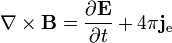	$\nabla \times \mathbf{B} = \frac{\partial \mathbf{E}} {\partial t} + 4 \pi \mathbf{j}_\mathrm{e}$	Em alguns casos, como guias de onda ou na cavidade de ressonância, a região de solução é, em grande parte isolado a partir do universo, por exemplo, por paredes metálicas, e condições de contorno nas paredes definem os campos com influência do mundo exterior confinada às extremidades de entrada / saída a estrutura. Em outros casos, o universo em geral é, por vezes, aproximadas através de um contorno absorvente artificial, ou, por exemplo, para irradiar as antenas ou os satélites de comunicações, estas condições de contorno podem assumir a forma de limites assimptóticas impostas à solução. Além disso, por exemplo, numa fibra óptica ou óptica de película fina, a região a solução muitas vezes é dividido em sub-regiões com as suas próprias propriedades simplificados, e as soluções em cada sub-região devem ser unidas uma à outra através das interfaces de sub-região, utilizando condições de contorno. Um exemplo particular desta utilização de condições de contorno é a substituição de um material com um volume de polarização por uma camada de superfície carregada, ou de um material com um volume de magnetização por uma corrente de superfície, como descrito na secção de carga e corrente encadernado . A seguir estão alguns links de carácter geral em matéria de problemas de valor limite: Exemplos de problemas de valor de contorno, teoria de Sturm-Liouville, Dirichlet condição de contorno, Neumann condição de contorno, condição de fronteira mista, Cauchy condição de contorno, condição de radiação Sommerfeld. Escusado será dizer, é preciso escolher as condições de contorno apropriadas para o problema que está sendo resolvido. Veja também Kempel e no livro de Friedman. Unidades de Gauss Unidades de Gauss é um popular variante eletromagnetismo do segundo sistema centímetros grama de unidades (CGS). Em unidades de Gauss, as equações de Maxwell são: $\nabla \cdot \mathbf{D} = 4\pi\rho_\mathrm{f}$ $\ Nabla \ cdot \ mathbf {B} = 0$ $\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}} {\partial t}$ $\nabla \times \mathbf{H} = \frac{1}{c} \frac{\partial \mathbf{D}} {\partial t} + \frac{4\pi}{c} \mathbf{J}_\mathrm{f}$ em que c é a velocidade da luz no vácuo. As equações microscópicas são: $\nabla \cdot \mathbf{E} = 4\pi\rho_{\mathrm{tot}}$ $\ Nabla \ cdot \ mathbf {B} = 0$ $\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}} {\partial t}$ $\nabla \times \mathbf{B} = \frac{1}{c} \frac{\partial \mathbf{E}}{\partial t} + \frac{4\pi}{c}\mathbf{J}_{\mathrm{tot}}.$ A relação entre ocampo deslocamento elétrico,campo elétricoedensidade de polarização é: $\mathbf{D} = \mathbf{E} + 4\pi\mathbf{P}.$ E da mesma forma a relação entre indução magnética,campo magnético e total demagnetização é: $\mathbf{B} = \mathbf{H} + 4\pi\mathbf{M}.$ Na aproximação linear, asensibilidade eléctrica ede susceptibilidade magnética são definidos de modo a que: 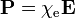$\mathbf{P} = \chi_\mathrm{e} \mathbf{E}$ , $\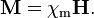mathbf{M} = \chi_\mathrm{m} \mathbf{H}.$ (Nota:. 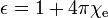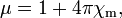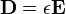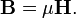Embora as suscetibilidades são números adimensionais em ambos os CGS e SI, eles diferem em valor por um fator de 4π) A permissividade e permeabilidade são: $\ \epsilon = 1+4\pi\chi_\mathrm{e}$ , $\ \mu = 1+4\pi\chi_\mathrm{m},$ de modo que $\mathbf{D} = \epsilon \mathbf{E}$ , $\mathbf{B} = \mu \mathbf{H}.$ Em vácuo,ε=μ= 1, portanto,D=E, eB=H. A força exercida sobre uma partícula carregada por umcampo eléctricoedo campo magnético é dada pelaequação da força de Lorentz: $\mathbf{F} = q \left(\mathbf{E} + \frac{\mathbf{v}}{c} \times \mathbf{B}\right),$ em que q é a carga sobre a partícula e v é a velocidade da partícula. Esta é ligeiramente diferente da expressão SI-unidade acima. Por exemplo, o campo magnético B tem as mesmas unidades que o campo eléctrico E . Algumas equações no artigo são dadas em unidades de Gauss, mas não SI ou vice-versa. Felizmente, existem regras gerais para converter de um para o outro; consulte o artigo unidades de Gauss para obter detalhes. Formulações alternativas de equações de Maxwell A relatividade especial motivou uma formulação matemática compacto das equações de Maxwell, em termos detensores covariantes.A mecânica quânticatambém motivou outras formulações. Por exemplo, considere um condutor que se move no campo de um ímã. No armação do ímã, que experimenta um condutor magnético vigor. Mas, no quadro de um condutor que se move em relação ao ímã, o condutor experimenta uma força devido a um elétrico campo. A formulação a seguir mostra como as equações de Maxwell assumir a mesma forma em qualquer sistemas de coordenadas inerciais. Formulação covariante das equações de Maxwell Na relatividade especial, a fim de expressar mais claramente o fato de que as equações de Maxwell ('microscópicas') tomam a mesma forma em qualquer sistema de coordenadas inercial, as equações de Maxwell são escritas em termos de quatro vetores e tensores no "manifestamente forma covariante ". Os componentes puramente espaciais da seguinte estão em Unidades SI. Um ingrediente nesta formulação é otensor eletromagnético, uma antisymmetric covariant rank-2tensor combinando os campos elétricos e magnéticos: $F_{\alpha \beta} = \left( \begin{matrix} 0 & \frac{-E_\mathrm{x}}{c} & \frac{-E_\mathrm{y}}{c} & \frac{-E_\mathrm{z}}{c} \\ \frac{E_\mathrm{x}}{c} & 0 & B_\mathrm{z} & -B_\mathrm{y} \\ \frac{E_\mathrm{y}}{c} & -B_\mathrm{z} & 0 & B_\mathrm{x} \\ \frac{E_\mathrm{z}}{c} & B_\mathrm{y} & -B_\mathrm{x} & 0 \end{matrix} \right)$ e o resultado de elevar os seus índices $F^{\mu \nu} \, \stackrel{\mathrm{def}}{=} \, \eta^{\mu \alpha} \, F_{\alpha \beta} \, \eta^{\beta \nu} = \left( \begin{matrix} 0 & \frac{E_\mathrm{x}}{c} & \frac{E_\mathrm{y}}{c} & \frac{E_\mathrm{z}}{c} \\ \frac{-E_\mathrm{x}}{c} & 0 & B_\mathrm{z} & -B_\mathrm{y} \\ \frac{-E_\mathrm{y}}{c} & -B_\mathrm{z} & 0 & B_\mathrm{x} \\ \frac{-E_\mathrm{z}}{c} & B_\mathrm{y} & -B_\mathrm{x} & 0 \end{matrix} \right).$ O outro componente é oquatro atual: $J^{\alpha} = (c\rho,\vec{J})$ ondeρé adensidade de carga eJé adensidade de corrente. Com estes ingredientes, as equações de Maxwell podem ser escritos: $\mu_{0} \, J^{\beta} \, = \, {\partial F^{\beta\alpha} \over {\partial x^{\alpha}} } \, \stackrel{\mathrm{def}}{=} \, \partial_{\alpha} F^{\beta\alpha} \, \stackrel{\mathrm{def}}{=} \, {F^{\beta\alpha}}_{,\alpha} \,$ e $0 = \partial_{\gamma} F_{\alpha\beta} + \partial_{\beta} F_{\gamma\alpha} + \partial_{\alpha} F_{\beta\gamma} \ \stackrel{\mathrm{def}}{=}\ {F_{\alpha\beta}}_{,\gamma} + {F_{\gamma\alpha}}_{,\beta} +{F_{\beta\gamma}}_{,\alpha}.$ A primeira equação tensor é uma expressão das duas equações de Maxwell não homogéneos, a lei de Gauss e lei de Ampère com a correção de Maxwell. A segunda equação é uma expressão das duas equações homogêneas, lei de indução de Faraday e lei de Gauss para o magnetismo. 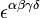A segunda equação é equivalente a $0 = \epsilon^{\delta\alpha\beta\gamma} {F_{\beta\gamma}}_{,\alpha}$ onde $\, \epsilon^{\alpha\beta\gamma\delta}$ é a versão contravariant dosímbolo Levi-Civita, e ${ \partial \over { \partial x^{\alpha} } } \ \stackrel{\mathrm{def}}{=}\ \partial_{\alpha} \ \stackrel{\mathrm{def}}{=}\ {}_{,\alpha} \ \stackrel{\mathrm{def}}{=}\ \left(\frac{1}{c}\frac{\partial}{\partial t}, \nabla\right)$ é o 4-gradiente. Nas equações de tensores acima, os índices repetidos são somados mais de acordo com a convenção de Einstein somatório. Temos exibidos os resultados em várias notações comuns. Componentes superior e inferior de um vector, v ^α e v ^α , respectivamente, são permutadas com o tensor fundamentais g , por exemplo, g = η = diag (-1, 1, 1, 1). Covariantes apresentações alternativas de equações de Maxwell também existem, por exemplo, em termos dequatro potencial; ver formulação covariante de eletromagnetismo clássico para mais detalhes. Formulação potencial Em mecânica clássica avançados e na mecânica quântica (onde é necessário) às vezes é útil para expressar as equações de Maxwell em uma "formulação potencial 'envolvendo o potencial elétrico (também chamado de potencial escalar), φ , eo potencial magnético, A , (também chamado potencial vetor). Estas são definidas de tal modo que: $\mathbf E = - \mathbf \nabla \varphi - \frac{\partial \mathbf A}{\partial t},$ $\mathbf B = \mathbf \nabla \times \mathbf A.$ Com estas definições, as duas equações homogêneas de Maxwell (Lei de Faraday e lei de Gauss para o magnetismo) são automaticamente satisfeitos e os outros dois (não homogéneos) equações dar as seguintes equações (por "equações microscópicas de Maxwell"): $\nabla^2 \varphi + \frac{\partial}{\partial t} \left ( \mathbf \nabla \cdot \mathbf A \right ) = - \frac{\rho}{\varepsilon_0}$ $\left ( \nabla^2 \mathbf A - \frac{1}{c^2} \frac{\partial^2 \mathbf A}{\partial t^2} \right ) - \mathbf \nabla \left ( \mathbf \nabla \cdot \mathbf A + \frac{1}{c^2} \frac{\partial \varphi}{\partial t} \right ) = - \mu_0 \mathbf J.$ Essas equações, tomados em conjunto, são tão poderosas e completas como as equações de Maxwell. Além disso, se trabalharmos apenas com os potenciais e ignorar os campos, o problema foi reduzido um pouco, já que os campos elétricos e magnéticos cada um tem três componentes que precisam ser resolvidos para (seis componentes no total), enquanto os potenciais elétricos e magnéticos têm apenas quatro componentes completamente. Muitas opções diferentes de A e φ são consistentes com um dado E e B , fazendo com que estas escolhas fisicamente equivalente - uma flexibilidade conhecida como a liberdade de calibre. Escolha adequada de A e φ pode simplificar essas equações, ou pode adaptá-los para atender a uma situação particular. Quatro potencial No Calibre de Lorentz, as duas equações que representam os potenciais pode ser reduzida para um manifestamenteequação invariante de Lorentz, usandoquatro vectores: aquatro corrente definida pela $j^\mu = \left( \rho c, \mathbf{j} \right)$ formado a partir da densidade de correnteje densidade de carga ρ, e aelectromagnética de quatro potencial definido pela $A^\mu = \left( \varphi , \mathbf{A} c \right)$ formado a partir do potencial vectorUme o potencial escalar 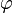$\varphi \,$ .A equação único resultante, devido aArnold Sommerfeld, uma generalização de uma equação devido aBernhard Riemanne conhecida como a equação de Riemann-Sommerfeld ou a forma covariante das equações de Maxwell, é: 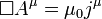$\Box A^\mu = \mu_0 j^\mu$ , onde 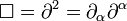$\Box=\partial^2=\partial_\alpha\partial^\alpha$ é o d'operador Alembertiano, ou quatro Laplacian, 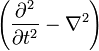$\left( {\partial^2 \over \partial t^2} - \nabla^2 \right)$ , escrita às vezes 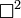$\Box^2$ Ou $\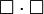Box \cdot \Box$ , Onde $\Box$ é o quatro gradiente. Formulações diferenciais Em espaço livre, onde ε = ε ₀ e μ = μ ₀ são constantes em toda parte, as equações de Maxwell simplificar consideravelmente uma vez que a linguagem da geometria diferencial e formas diferenciais é usado. No que se segue, unidades CGS-Gauss, não são utilizados unidades SI. (Para converter a SI, consulte aqui.) Os campos elétricos e magnéticos são descritos agora em conjunto por um 2-forma F em um 4-dimensional colector de espaço-tempo. As equações de Maxwell então se reduzem à identidade de Bianchi $\mathrm{d}\bold{F}=0$ onde d denota aderivada exterior - natural coordenar e métrica operador diferencial independente agindo em formas - ea equação fonte $\mathrm {d} * {\bold{F}}=\bold{J}$ onde o (dual)Hodge operador de estrela * é uma transformação linear do espaço de 2-formas para o espaço de (4-2) -forms definido pela métrica noespaço Minkowski (em quatro dimensões ainda por qualquer métricaconformada para essa métrica ), e os campos estão emunidades singulares, onde 1 / 4π£ ₀= 1. Aqui, a forma 3-Jé chamado aforma de corrente eléctricaou de corrente 3-formaque satisfaça aequação de continuidade $\mathrm{d}{\bold{J}}=0.$ O atual 3-forma pode ser integrado sobre uma região do espaço-tempo 3-dimensional. A interpretação física deste integrante é a taxa em que a região se for de tipo espaço, ou a quantidade de carga que flui através de uma superfície num determinado período de tempo se que a região é uma superfície de tipo espaço atravessar um intervalo de tipo tempo. Como derivado exterior é definida em qualquer colector , a versão de forma diferencial a identidade Bianchi faz sentido para qualquer colector 4-dimensional, enquanto que a equação de origem está definida se o colector está orientado e tem uma métrica de Lorentz. Em particular, a versão forma diferencial das equações de Maxwell são uma formulação conveniente e intuitiva das equações de Maxwell na relatividade geral. Em uma forma linear, a teoria macroscópica, a influência da matéria no campo electromagnético é descrito através de transformação linear mais geral no espaço de 2-formas. Nós chamamos $C:\Lambda^2\ni\bold{F}\mapsto \bold{G}\in\Lambda^{(4-2)}$ a transformação constitutiva. O papel desta transformação é comparável à transformação dualidade Hodge. As equações de Maxwell na presença de matéria, em seguida, tornar-se: $\mathrm{d}\bold{F} = 0$ $\mathrm{d}\bold{G} = \bold{J}$ onde o 3-forma atualJainda satisfaz a continuidade equação dJ= 0. Quando os campos são expressos como combinações lineares (doexterior) de produtos de base formuláriosθ^p, $\bold{F} = \frac{1}{2}F_{pq}\bold{\theta}^p\wedge\bold{\theta}^q.$ a relação constitutiva assume a forma $G_{pq} = C_{pq}^{mn}F_{mn}$ em que as funções de coeficiente campo são anti-simétrico nos índices e os coeficientes constitutivos são anti-simétrico nos pares correspondentes. Em particular, a transformação dualidade Hodge que conduz às equações de vácuo discutidos acima são obtidos tomando $C_{pq}^{mn} = \frac{1}{2}g^{ma}g^{nb} \epsilon_{abpq} \sqrt{-g}$ que até dimensionamento é o único tensor invariante deste tipo que podem ser definidos com a métrica. Nesta formulação, eletromagnetismo generaliza imediatamente a qualquer colector orientado 4-dimensional ou com pequenas adaptações qualquer variedade, necessitando nem mesmo uma métrica. Assim, a expressão das equações de Maxwell em termos de formas diferenciais leva a uma maior simplificação de notação e conceitual. Considerando que as equações de Maxwell poderia ser escrito como duas equações tensoriais em vez de oito equações escalares, a partir do qual a propagação de perturbações eletromagnéticas ea equação de continuidade poderia ser derivados com um pouco de esforço, utilizando formas diferenciais leva a uma derivação ainda mais simples destes resultados. Visão conceitual a partir desta formulação No lado conceitual, do ponto de vista da física, isto mostra que as segunda e terceira equações de Maxwell deve ser agrupados em conjunto, ser chamado os homogéneas, e ser visto como geométrico identidades expressam nada mais do que: o campo F deriva de uma mais "fundamental" potencial A . Enquanto o primeiro eo último deve ser visto como as dinâmico equações de movimento , obtidas por meio do princípio de Lagrange de ação mínima, desde o "termo de interação" AJ (introduzido através de bitola derivados covariantes), o acoplamento do campo à matéria. Muitas vezes, o derivado vez na terceira lei motiva chamando essa equação "dinâmica", que é um pouco enganoso; no sentido da análise precedente, isto é, em vez de um artefacto de quebrar relativista covariância escolhendo num sentido de tempo preferido. Para ter graus físicos de liberdade propagada por essas equações de campo, deve-se incluir um termo cinético *F F para A ; e ter em conta os graus não-físicos de liberdade que podem ser removidos por transformação calibre A → A ' = A -. dα Veja também avaliar fixação e Faddeev-Popov fantasmas. Álgebra formulação geométrica (GA) Em álgebra geométrica, as equações de Maxwell são reduzidos a uma única equação, $\left(\frac{1}{c}\partial_t + \boldsymbol{\nabla}\right)F = \mu_0 c J,$ ondeFeJsão multivectors $F = \bold{E} + Ic\bold{B}$ e $J = c \rho + \bold{J}.$ com a unidadepseudoescalarI ²= -1 O GA operador gradiente espacial∇atua em um campo vetorial, de tal forma que $\boldsymbol{\nabla}\bold{F} = \boldsymbol{\nabla} \cdot \bold{F} + I \boldsymbol{\nabla} \times \bold{F},$ Em álgebra espaço-tempo, usando o mesmo produto geométrico a equação é simplesmente $\nabla F = \mu_0 c J,$ o derivado do espaço-tempo do campo eletromagnético é sua fonte. Aqui o (não negrito) gradiente de espaço-tempo $\nabla = \gamma^\mu \partial_\mu$ é um vector de quatro, como seja a densidade de corrente $J = \gamma_{\mu} J^{\mu} = \gamma_0 c \rho + J^k \gamma_k = (c \rho + \bold{J})\gamma_0.$ Para uma demonstração de que as equações dadas reproduzir as equações de Maxwell veja o artigo principal. Eletrodinâmica clássica como a curvatura de um pacote de linha Uma forma elegante e intuitivo para formular as equações de Maxwell é a utilização de complexos feixes de linha ou feixes principais com fibra de L (1). O conexão $\ Nabla$ no pacote de linha tem uma curvatura 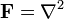$\bold{F} = \nabla^2$ que é um de dois forma que automaticamente satisfaz 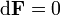$\mathrm{d}\bold{F} = 0$ e pode ser interpretado como um campo de força- . Se o pacote de linha é trivial com referência plana conexão d podemos escrever 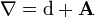$\nabla = \mathrm{d}+\bold{A}$ e F = d Um com A a 1-forma composta pelo potencial elétrico eo potencial vetor magnético. Em mecânica quântica, a própria ligação é utilizada para definir a dinâmica do sistema. Esta formulação permite uma descrição natural do efeito Aharonov-Bohm. Neste experimento, um campo magnético estático é executado através de um fio magnético longo (por exemplo, um fio de ferro magnetizado longitudinalmente). Fora deste fio a indução magnética é zero, em contraste com o potencial vector, que depende essencialmente do fluxo magnético através da secção transversal do arame e não desaparece fora. Uma vez que não existe um campo eléctrico seja, o tensor de Maxwell F = 0** em toda a região de espaço-tempo no exterior do tubo, durante a experiência. Isto significa, por definição, que a conexão $\ Nabla$ é plana lá. No entanto, como mencionado, a ligação depende do campo magnético através do tubo desde o holonomia ao longo de uma curva não-contráctil que rodeia o tubo é o fluxo magnético através do tubo nas unidades apropriadas. Isso pode ser detectado quantum-mecanicamente com uma dupla fenda experimento de difração de elétrons em uma onda de elétrons viajando ao redor do tubo. A holonomia corresponde a um desvio de fase adicional, o que leva a uma mudança no padrão de difracção. Espaço-tempo curvo Formulação tradicional Matéria e energia gerar curvatura espaço-tempo. Este é o tema da relatividade geral . Curvatura do espaço-tempo afeta eletrodinâmica. Um campo eletromagnético que tem energia e momento também gera curvatura no espaço-tempo. As equações de Maxwell no espaço-tempo curvo pode ser obtido através da substituição dos derivados nas equações no espaço-tempo plano com derivados covariantes. as equações de origem e livre de código-fonte tornar-se ((Se esta é a generalização adequada requer investigação separada.) CGS-Gauss unidades): ${ 4 \pi \over c }j^{\beta} = \partial_{\alpha} F^{\alpha\beta} + {\Gamma^{\alpha}}_{\mu\alpha} F^{\mu\beta} + {\Gamma^{\beta}}_{\mu\alpha} F^{\alpha \mu} \ \stackrel{\mathrm{def}}{=}\ D_{\alpha} F^{\alpha\beta} \ \stackrel{\mathrm{def}}{=}\ {F^{\alpha\beta}}_{;\alpha} \, \!$ e $0 = \partial_{\gamma} F_{\alpha\beta} + \partial_{\beta} F_{\gamma\alpha} + \partial_{\alpha} F_{\beta\gamma} = D_{\gamma} F_{\alpha\beta} + D_{\beta} F_{\gamma\alpha} + D_{\alpha} F_{\beta\gamma}.\,$ Aqui, ${\Gamma^{\alpha}}_{\mu\beta} \!$ é um Símbolo christoffel que caracteriza a curvatura do espaço-tempo eD_γé o derivado covariante. Formulação em termos de formas diferenciais A formulação das equações de Maxwell em termos de formas diferenciais podem ser usados sem alteração na relatividade geral. A equivalência das relativística a formulação mais tradicional geral usando o derivado covariante com a formulação de forma diferencial pode ser vista como se segue. Escolha coordenadas locais x ^α que dá uma base de 1-formas d x ^α em todos os pontos do conjunto aberto, onde as coordenadas são definidas. Usando esta base e unidades CGS-Gauss definimos O tensor de campo infinitesimal antissimétrico 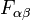$F_{\alpha\beta}$ , correspondente ao campo de 2 formaF $\bold{F} := \frac{1}{2}F_{\alpha\beta} \,\mathrm{d}\,x^{\alpha} \wedge \mathrm{d}\,x^{\beta}.$ A corrente de vetor 3-forma infinitesimalJ $\bold{J} := {4 \pi \over c } j^{\alpha} \sqrt{-g} \, \epsilon_{\alpha\beta\gamma\delta} \mathrm{d}\,x^{\beta} \wedge \mathrm{d}\,x^{\gamma} \wedge \mathrm{d}\,x^{\delta}.$ Aquigé, como de costume o determinante do tensor métrico 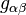$g_{\alpha\beta}$ .Um pequeno cálculo que usa a simetria dossímbolos de Christoffel (ou seja, a torção-franqueza daconexão Levi Civita) eo constantness covariant dooperador de estrela Hodge, em seguida, mostra que neste coordenar bairro temos: a identidade Bianchi $\mathrm{d}\bold{F} = 2(\partial_{\gamma} F_{\alpha\beta} + \partial_{\beta} F_{\gamma\alpha} + \partial_{\alpha} F_{\beta\gamma})\mathrm{d}\,x^{\alpha}\wedge \mathrm{d}\,x^{\beta} \wedge \mathrm{d}\,x^{\gamma} = 0,$ a equação fonte $\mathrm{d} * \bold{F} = {F^{\alpha\beta}}_{;\alpha}\sqrt{-g} \, \epsilon_{\beta\gamma\delta\eta}\mathrm{d}\,x^{\gamma} \wedge \mathrm{d}\,x^{\delta} \wedge \mathrm{d}\,x^{\eta} = \bold{J},$ a equação de continuidade $\mathrm{d}\bold{J} = { 4 \pi \over c } {j^{\alpha}}_{;\alpha} \sqrt{-g} \, \epsilon_{\alpha\beta\gamma\delta}\mathrm{d}\,x^{\alpha}\wedge \mathrm{d}\,x^{\beta} \wedge \mathrm{d}\,x^{\gamma} \wedge \mathrm{d}\,x^{\delta} = 0.$