
Ímpeto
Informações de fundo
Crianças SOS, que corre cerca de 200 sos escolas no mundo em desenvolvimento, organizado esta selecção. Patrocinar crianças ajuda crianças no mundo em desenvolvimento para aprender também.
| A mecânica clássica |
|---|
|
Ramos
|
Formulações Mecânica analítica ( Mecânica lagrangiana Mecânica hamiltoniana) |
Conceitos fundamentais
|
Temas centrais Corpo rígido
Lei de Newton gravitação universal
Inercial / Não-inercial quadro de referência
Mecânica de planar partícula movimento
|
Movimento de rotação Movimento circular
Força centrífuga
|

Em mecânica clássica , momentum ( pl. momentos; Unidade SI kg · m / s, ou, de forma equivalente, N · s) é o produto da massa e da velocidade de um objecto (p = mv). Para medidas mais precisas da dinâmica, consulte a seção "definições modernas de impulso" nesta página. É por vezes referido como o impulso linear para distingui-lo do assunto relacionado do momento angular . Momento linear é um grandeza vectorial, uma vez que tem uma direcção, bem como uma amplitude. O momento angular é uma quantidade pseudovetor porque ganha uma aleta sinal adicional no âmbito de um rotação indevido o momento total de todos os grupos de objectos permanece a mesma, a menos que as forças externas actuam sobre o objecto.
Momentum é um conservada quantidade, o que significa que a dinâmica total de qualquer sistema fechado (um não foi afectada por forças externas) não pode mudar.
História do conceito
A palavra eo conceito geral de impulso foi utilizado no República Romana principalmente para significar "um movimento, movimento (como uma força habitação ...)." Um peixe foi capaz de mudar de velocidade (Velocitas) através do impulso de sua cauda. A palavra é formada por um acréscimo de suficiente sobre a haste de Latina Movere, "mover". A movi-Men é o resultado da Movere tão frag-Men é o resultado de frangere, "para quebrar". Prorrogação por -Para- obtém mōvimentum e Fragmentum, o ex-adjudicante impulso.
O momento não era apenas o movimento, que foi Motus, mas era o poder que reside em um objeto em movimento, capturado por definições matemáticas de hoje. A Motus, "movimento", era um estágio em qualquer tipo de mudança, enquanto Velocitas, "rapidez", única capturado velocidade. Os romanos, devido a limitações inerentes ao numeral romano sistema, foram incapazes de ir mais longe com a percepção.
A chegada de algarismos árabes no século 10 abriu o portão para a filosofia moderna quantitativa. O conceito do momento na mecânica clássica foi originada por uma série de grandes pensadores e experimentalistas. O primeiro deles foi Ibn Sina (Avicena) circa 1000, que se referiu a como impulso proporcional ao vezes o peso velocidade . René Descartes mais tarde se refere aos tempos de velocidade de massa como a força fundamental do movimento. Galileo na sua Duas Novas Ciências usou o italiano palavra "impeto."
A questão tem sido muito debatida, como o que Sir Isaac Newton foi a contribuição 's para o conceito. Aparentemente nada, exceto para o estado mais plenamente e com melhores a matemática o que já era conhecido. O primeiro e segundo de Leis de Newton já havia sido afirmado por John Wallis em 1670 seu trabalho, Mechanica sive De Motu, Tractatus geometricus: "o estado inicial do corpo, seja de repouso ou de movimento, persistirá" e "Se a força é maior que a resistência, o movimento vai resultar ... . "Wallis usa ímpeto e força para vis.
De Newton "Princípios Matemáticos da História Natural", quando ele saiu primeiro em 1686 mostrou um casting semelhante em torno de palavras usar para a dinâmica matemática. Seus define Definição II quantitas motus, "quantidade de movimento", como "decorrente da velocidade e quantidade de matéria conjuntamente", que identifica-lo como impulso. Assim, quando em Direito II ele se refere a Mutatio motus, "mudança de movimento", sendo proporcional à força impressionado, ele é geralmente entendida no sentido de impulso e não o movimento.
Manteve-se apenas para atribuir um termo padrão para a quantidade de movimento. O primeiro uso do "momentum" em seu sentido matemático adequado não está claro, mas pelo tempo de Miscelânea de Jenning em 1721, quatro anos antes da edição final do de Newton Principia Mathematica, o momento M ou "quantidade de movimento" estava a ser definido para os alunos como "um rectângulo", o produto de Q e V, em que Q é "quantidade de material" e V é "velocidade", S / T.
Momento linear de uma partícula

Se um objeto está se movendo em qualquer quadro de referência, então ele tem ímpeto nesse quadro. É importante notar que o movimento é enquadrar dependente. Isto é, o mesmo objecto pode ter uma certa quantidade de movimento em um quadro de referência, mas uma quantidade diferente de um outro quadro. Por exemplo, um objecto móvel tem impulso num quadro de referência fixo a um ponto na terra, enquanto ao mesmo tempo tendo 0 impulso num referencial ligado ao objecto do centro de massa .
A quantidade de momento que um objecto tem depende de duas grandezas físicas: a massa e a velocidade do objecto em movimento no quadro de referência. Na física, o símbolo usual para impulso é uma pequena p negrito (bold porque é um vetor ); de modo que este pode ser escrita:
onde:
 é o impulso
é o impulso  é a massa
é a massa  a velocidade
a velocidade
Exemplo: um modelo de avião de 1 kg que viajam para o norte a 1 m / s em vôo reto e tem uma dinâmica de 1 kg m / s, para norte, medidos a partir do solo. Para o piloto manequim no cockpit tem uma velocidade e dinâmica de zero.
De acordo com a segunda lei de Newton, a taxa de variação do momento de uma partícula é proporcional à força resultante actuando sobre a partícula e é, no sentido de que a força. No caso de uma massa constante, e velocidades muito menos do que a velocidade da luz, esta definição resulta na equação
ou simplesmente
onde F é entendido como sendo a resultante .
Exemplo: um modelo de avião de 1 kg acelera de resto a uma velocidade de 1 m / s, para norte, em 1 segundo. A pressão necessária para produzir esta aceleração é 1 newton. A mudança de impulso é de 1 kg-m / s. Para o piloto manequim no cockpit não há nenhuma mudança de momentum. Sua pressionando para trás no banco é uma reação ao impulso desequilibrado, prestes a ser em relação ao arrasto.
Momento linear de um sistema de partículas
Relativo a massa e velocidade
O movimento linear de um sistema de partículas é o vector soma dos momentos de todos os objectos individuais no sistema.
onde
 é a dinâmica do sistema de partículas
é a dinâmica do sistema de partículas  é a massa do objeto i
é a massa do objeto i 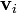 o vetor velocidade do objeto i
o vetor velocidade do objeto i  é o número de objectos no sistema
é o número de objectos no sistema
Pode ser mostrado que, no centro de massa a dinâmica de um sistema é zero. Além disso, o impulso em um quadro de referência que está se movendo a uma velocidade  no que diz respeito a esse quadro é simplesmente:
no que diz respeito a esse quadro é simplesmente:
onde:
 .
.
Relativo a force- Equações gerais do movimento

O movimento linear de um sistema de partículas também pode ser definida como o produto da massa total  do sistema vezes a velocidade do centro de massa
do sistema vezes a velocidade do centro de massa 
Isto é vulgarmente conhecida como a segunda lei de Newton .
Para uma derivação mais geral usando tensores, consideramos um corpo em movimento (ver Figura), assume-se como um contínuo, ocupando um volume  de uma vez
de uma vez  , Tendo uma área de superfície
, Tendo uma área de superfície  , Com tracção ou de superfície forças definidos
, Com tracção ou de superfície forças definidos  que actuam em todos os pontos da superfície do corpo, as forças de corpo
que actuam em todos os pontos da superfície do corpo, as forças de corpo  por unidade de volume em cada ponto dentro do volume
por unidade de volume em cada ponto dentro do volume  , E um campo de velocidades
, E um campo de velocidades  prescritos em todo o corpo. Seguindo a equação anterior, O movimento linear do sistema é:
prescritos em todo o corpo. Seguindo a equação anterior, O movimento linear do sistema é:
Por definição, o estresse vetor é  , Então
, Então
Usando o Divergência teorema de Gauss para converter uma superfície integrante de um integrante do volume dá
Para um volume arbitrário do integrando desaparece, e temos equações de movimento do Cauchy
Se um sistema está em equilíbrio, a mudança de impulso em relação ao tempo é igual a 0, como não há nenhuma aceleração.
ou usando tensores,
Estas são as equações de equilíbrio que são utilizados em mecânica dos sólidos para resolver problemas de elasticidade linear. Na notação de engenharia, as equações de equilíbrio são expressos como
Conservação do momento linear
A lei da conservação do momento linear é uma lei fundamental da natureza, e afirma que o momento total de um sistema fechado de objetos (que não tem interações com agentes externos) é constante. Uma das consequências disto é que o centro de massa de qualquer sistema de objetos sempre continuar com a mesma velocidade, a menos que actuado por uma força de fora do sistema.
Conservação do momento é uma consequência matemática da homogeneidade (shift simetria ) de espaço (posição no espaço é o quantidade conjugado canônica impulso). Então, conservação do momento pode ser filosoficamente declarou como "nada depende da localização per se".
Em um sistema isolado (aquele em que forças externas estão ausentes) o momento total será constante: isto está implícito por Newton primeira lei do movimento. A terceira lei de Newton, a lei de ações recíprocas , que dita que as forças que atuam entre os sistemas são iguais em magnitude, mas de sinal contrário, é devido à conservação de momento.
Uma vez que a posição no espaço é uma grandeza vectorial, impulso (sendo o conjugado canônica de posição) é uma grandeza vetorial bem - tem direção. Assim, quando uma arma é disparada, o momento total final do sistema (a arma ea bala) é a soma vetorial dos momentos destes dois objetos. Assumindo que a arma e bala estivesse em repouso antes de disparar (o que significa o impulso inicial do sistema era zero), o momento total final deve também igual a 0.
Em um sistema isolado com apenas dois objectos, a mudança no momento de um objecto deve ser igual e oposta à alteração na quantidade de movimento do outro objecto. Matematicamente,

Impulso tem a propriedade especial que, numa sistema fechado, que é sempre conservada, mesmo em colisões e separações causadas por forças explosivas. A energia cinética , por outro lado, não é conservada em colisões se forem inelástica. Uma vez que o impulso é conservada que pode ser utilizado para calcular uma velocidade desconhecido após uma colisão ou uma separação, se todas as outras massas e velocidades são conhecidos.
Um problema comum na física que requer a utilização deste facto é a colisão de duas partículas. Desde o momento é sempre conservada, a soma dos momentos antes da colisão deve ser igual à soma dos momentos após a colisão:
onde:
- u significa vector de velocidade antes da colisão
- v significa vector de velocidade após a colisão.
Geralmente, nós só sabemos ou as velocidades antes ou depois de uma colisão e gostaria também para descobrir o oposto. Corretamente resolver este problema significa que você tem que saber que tipo de colisão ocorreu. Existem dois tipos básicos de colisões, sendo que ambos conservar o momento:
- Colisões elásticas conservar energia cinética, bem como o impulso total antes e após a colisão.
- Colisões inelásticas não conservar energia cinética, mas impulso total antes e após a colisão é conservada.
Colisões elásticas
Uma colisão entre dois bolas de bilhar é um bom exemplo de uma colisão quase totalmente elástica. Além de impulso a ser conservada quando as duas esferas colidem, a soma de energia cinética antes de uma colisão deve ser igual à soma da energia cinética após:
Uma vez que o factor de 1/2 é comum a todos os termos, que podem ser retirados imediatamente.
Colisão frontal (1 dimensional)
No caso de dois objetos colidem cabeça em nós achamos que a velocidade final
que pode então facilmente ser reorganizada para
Caso especial: m 1 m 2 >>
Considere agora o caso quando a massa de um corpo, por exemplo 1 m, é muito maior do que a do outro, 2 m (1 m >> m 2). Nesse caso m + 1 m 2 é aproximadamente igual a 1 m e 1 m -m 2 é aproximadamente igual a 1 m.
Usando estas aproximações, a fórmula acima para  reduz-se a
reduz-se a  . A sua interpretação física é que, no caso de uma colisão entre dois corpos, um dos quais é muito mais maciça do que o outro, o corpo de isqueiro termina-se movendo-se em sentido oposto com o dobro da velocidade inicial do corpo mais maciço.
. A sua interpretação física é que, no caso de uma colisão entre dois corpos, um dos quais é muito mais maciça do que o outro, o corpo de isqueiro termina-se movendo-se em sentido oposto com o dobro da velocidade inicial do corpo mais maciço.
Caso especial: m 1 = m 2
Outro caso especial é quando a colisão é entre dois corpos de massa igual.
Diga m1 corpo em movimento a uma velocidade v 1 ataques corpo m 2 que está em repouso (v 2). Colocar este caso na equação derivada acima, veremos que após a colisão, o corpo que estava se movendo (m 1) começará a se mover com velocidade v 2 ea massa m 2 começará a se mover com velocidade v 1. Portanto, vai haver uma troca de velocidades.
Agora, suponha que uma das massas, digamos m 2, estava em repouso. Nesse caso, após a colisão o corpo em movimento, m 1, virá para descansar e o corpo que estava em repouso, m 2, vai começar a se mover com a velocidade que sou um tinha antes da colisão.
Note-se que todas estas observações são para uma colisão elástica.
Este fenómeno é demonstrado pela Berço de Newton, um dos exemplos mais conhecidos de conservação do momento, um exemplo da vida real deste caso especial.
Colisões multi-dimensionais
No caso de objectos que colidem em mais de uma dimensão, como em colisões oblíquas, a velocidade é resolvido em componentes ortogonais com uma componente perpendicular ao plano de colisão e o outro componente ou componentes no plano de colisão. Os componentes de velocidade no plano de colisão permanecem inalteradas, enquanto que a velocidade perpendicular ao plano de colisão é calculado da mesma maneira como o caso unidimensional.
Por exemplo, em caso de colisão de duas dimensões, os momentos podem ser resolvidos em componentes x e y. Podemos então calcular cada componente separadamente, e combiná-los para produzir um resultado vetor. A grandeza deste vector é o momento final do sistema isolado.
Veja a Página colisão elástica para mais detalhes. 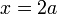
Colisões inelásticas
Um exemplo comum de uma colisão perfeitamente inelástica é quando duas bolas de neve colidem e, em seguida, ficar juntos depois. Esta equação descreve a conservação do momento:
Pode ser demonstrado que uma colisão perfeitamente inelástica é aquele em que a quantidade máxima de energia cinética é transformada em outras formas. Por exemplo, se os dois objectos se unem após a colisão e se movem com uma velocidade final comum, pode-se sempre encontrar um quadro de referência em que os objectos são, colocado em descanso pela colisão e 100% da energia cinética é convertido. Isso é verdadeiro mesmo no caso relativista e utilizados em aceleradores de partículas para converter eficientemente a energia cinética em novas formas de massa-energia (ou seja, para criar partículas massivas).
Em caso de colisão inelástica, existe um parâmetro chamado ligado coeficiente de restituição (indicado por pequenas "e" ou "c" em muitos livros de texto). É definida como a razão entre a velocidade relativa de separação a velocidade relativa de abordagem. É uma proporção, portanto, é uma quantidade adimensional.
Quando temos uma colisão elástica o valor de E (= coeficiente de restituição) é 1, isto é, a velocidade relativa de abordagem é o mesmo que a velocidade relativa de separação dos corpos de colisão. Em uma colisão elástica, a energia cinética do sistema é conservada.
Quando uma colisão não é elástico (E <1) é uma colisão elástica. No caso de uma colisão elástica perfeitamente a velocidade relativa de separação entre o centro de massas de corpos que colidem é 0. Logo após a colisão dos corpos ficar juntos após a colisão. No caso de uma colisão elástica a perda de energia cinética é máxima como indicado acima.
Em todos os tipos de colisão, se nenhuma força externa age sobre o sistema de corpos colidindo, o ímpeto sempre terá preservado.
Explosões
Uma explosão ocorre quando um objecto é dividido em dois ou mais fragmentos, devido a uma libertação de energia. Note-se que a energia cinética de um sistema de explosão não é conservada porque envolve a transformação de energia. (ou seja, mudanças de energia cinética em calor e energia do som)
http://www.glenbrook.k12.il.us/gbssci/phys/Class/momentum/u4l2e.html
Na demonstração canhão explodindo, impulso total do sistema é conservada. O sistema é composto por dois objetos - um canhão e uma bola de tênis. Antes da explosão, a quantidade de movimento total do sistema é igual a zero desde o canhão e a bola de ténis localizado dentro do mesmo são tanto em repouso. Após a explosão, o momento total do sistema ainda tem de ser zero. Se a bola adquire 50 unidades de impulso para a frente, em seguida, o canhão adquire 50 unidades de trás momentum. A soma vetorial dos momentos individual dos dois objetos é 0. impulso total do sistema é conservada.
Veja a Página colisão inelástica para mais detalhes.
Definições modernas de impulso
Momentum em mecânica relativista
Em mecânica relativista, a fim de ser conservado, o impulso deve ser definida como:
onde
 é o massa invariante do objeto em movimento,
é o massa invariante do objeto em movimento,  é o Fator de Lorentz
é o Fator de Lorentz  é a velocidade relativa entre um objecto e um observador
é a velocidade relativa entre um objecto e um observador  é a velocidade da luz .
é a velocidade da luz .
Dinâmica relativista também pode ser escrito como a massa vezes invariantes do objeto velocidade adequada, definida como a taxa de variação da posição do objecto na moldura observador em relação ao tempo decorrido em relógios de objectos (isto é objecto tempo adequado). Dinâmica relativista torna-se dinâmica newtoniana:  a baixa velocidade
a baixa velocidade  .
.
Relativistic quatro-momentum como proposto por Albert Einstein surge da invariância de quatro vectores em tradução Lorentzian. Os quatro-impulso é definido como:
onde
 é o
é o  componente da dinâmica relativística,
componente da dinâmica relativística, 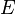 é a energia total do sistema:
é a energia total do sistema: 
O "tamanho" do vetor é a massa vezes a velocidade da luz, que é invariável para todos os quadros de referência:
Momentum de objetos sem massa
Objetos sem massa de repouso, como fótons , também carregam momentum. A fórmula é:
onde
 é A constante de Planck,
é A constante de Planck, 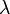 é o comprimento de onda do fóton,
é o comprimento de onda do fóton, 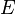 é a energia do fóton carrega e
é a energia do fóton carrega e  é a velocidade da luz .
é a velocidade da luz .
Generalização do momento
Momentum é a Noether carga de invariância translacional. Como tal, os campos pares, bem como outras coisas pode ter impulso, não apenas partículas. No entanto, no espaço-tempo que não é assintoticamente Minkowski, o momento não é definido em tudo.
Momentum na mecânica quântica
Na mecânica quântica , dinâmica é definida como uma operador na função de onda. O Heisenberg O princípio da incerteza define limites sobre a precisão do momento ea posição de um único sistema observável pode ser conhecido de uma vez. Na mecânica quântica, a posição eo momento são variáveis conjugado.
Para uma única partícula sem carga elétrica e não rotação, o operador impulso pode ser escrito na base de posição como
onde:
 é o operador de gradiente;
é o operador de gradiente; 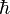 é o Planck reduzido constante;
é o Planck reduzido constante;  representa a unidade imaginária .
representa a unidade imaginária .
Esta é uma forma vulgarmente encontrado do operador de impulso, que não a mais geral.
Momentum em eletromagnetismo
Os campos eléctricos e magnéticos possuem impulso, independentemente de eles são estáticos ou mudam no tempo. É uma grande surpresa para calouros que são introduzidos para o bem conhecido fato de a pressão  de um campo eletrostático (magnetostático) sobre uma esfera de metal, capacidade cilíndrica ou bar ferromagnético:
de um campo eletrostático (magnetostático) sobre uma esfera de metal, capacidade cilíndrica ou bar ferromagnético:
onde  ,
,  ,
,  , São a densidade de energia eletromagnética, elétrica e campos magnéticos, respectivamente. A pressão electromagnética
, São a densidade de energia eletromagnética, elétrica e campos magnéticos, respectivamente. A pressão electromagnética  pode ser suficientemente alta para explodir capacidade. Assim, campos elétricos e magnéticos carregam momentum.
pode ser suficientemente alta para explodir capacidade. Assim, campos elétricos e magnéticos carregam momentum.
Light (visível, UV, rádio) é uma onda eletromagnética e também tem ímpeto. Mesmo que os fótons (aspecto partícula de luz) não têm massa, eles ainda carregam momentum. Isto resulta em aplicações tais como a vela solar.
Momentum é conservada em um sistema de eletrodinâmica (que pode mudar de impulso nos campos de impulso mecânico de partes móveis). O tratamento do impulso de um campo é normalmente realizado considerando a chamada tensor de energia-momento ea mudança no tempo do Poynting vector integrada sobre algum volume. Este é um campo tensor que tem componentes relacionadas com a densidade de energia ea densidade de momentum.
O momento canônico definição correspondente ao operador dinâmica da mecânica quântica quando interage com o campo eletromagnético é, usando o princípio de menos de engate:
 ,
,
em vez da habitual
 ,
,
onde:
 é o vetor potencial eletromagnético
é o vetor potencial eletromagnético 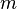 massa invariante da partícula carregada
massa invariante da partícula carregada  sua velocidade
sua velocidade 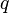 sua carga.
sua carga.
























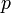 . Por favor, note que na notação utilizada pelo criador do diagrama, a massa invariante
. Por favor, note que na notação utilizada pelo criador do diagrama, a massa invariante 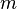 é subscrito com um zero,
é subscrito com um zero, 



![P_ {static} = {} W = [{\ epsilon_0 \ epsilon} {\ frac {{\ mathbf E} ^ 2} {{2}}} + {\ frac {1} {{\ mu_0 \ mu}}} {\ frac {{\ mathbf B} ^ 2} {{2}}}],](../../images/160/16078.png)
