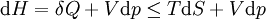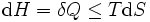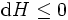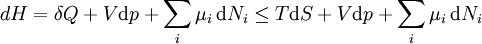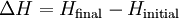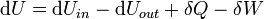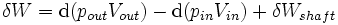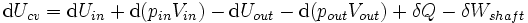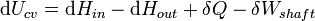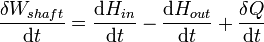Entalpía
Sabías ...
SOS Children, una organización benéfica educación , organizó esta selección. Haga clic aquí para obtener información sobre el apadrinamiento de niños.
| La mecánica estadística |
|---|
 |
|
Estadísticas de partículas
|
Conjuntos
|
|
Modelos
|
Potenciales
|
En la termodinámica y la química molecular , la entalpía o calor contenido (denotado como H, 'h', o raramente como χ) es un cociente o descripción de potencial termodinámico de un sistema, que puede ser utilizado para calcular el trabajo "útil" obtenible a partir de una cerrado sistema termodinámico bajo presión constante.
El término entalpía está compuesto por el prefijo en-, que significa "poner en" y el griego palabra -thalpein, que significa "calor", aunque la definición original se cree que procede de la palabra, "enthalpos" (ἐνθάλπος). Se calcula a menudo como una suma diferencial, que describe los cambios en exo- y endo térmicos , que minimizan las reacciones en equilibrio.
Historia
Sobre el historia de la termodinámica, varios términos se han utilizado para referirse a lo que hoy se conoce como la entalpía de un sistema. En un principio, se pensó que la palabra "entalpía" fue creado por Émile Clapeyron y Rudolf Clausius a través de la publicación de la Relación de Clausius-Clapeyron en "Las Tablas de Vapor Mollier y diagramas" en 1827 , pero se publicó después de que la primera grabación de la palabra en 1875 , por Josiah Willard Gibbs en la publicación "Química Física: un Tratado avanzada", aunque No se hace referencia en Gibbs trabaja directamente. En 1909 , Keith Landler discutió 'trabajo en el' Gibbs función de calor para la presión constante "y señaló que Heike Kamerlingh Onnes había acuñado su nombre moderno del griego palabra "enthalpos" (ενθαλπος) que significa "poner el calor en."
Definición original
Este es el cambio de calor que se produce cuando 1 mol de una sustancia reacciona completamente con el oxígeno para formar productos en 298 K y 1 atm. La función H fue introducido por el físico holandés Heike Kamerlingh Onnes en principios del siglo 20 en la siguiente forma:
donde E representa la energía del sistema. En ausencia de un campo externo, la entalpía puede ser definida, como es generalmente conocido, por:
donde (todas las unidades indicadas en SI)
- H es la entalpía ( joules)
- U es la energía interna, (julios)
- p es el presión del sistema, ( pascales)
- V es el volumen , ( metros cubicos)
Aplicación y la fórmula extendida
Visión de conjunto
En términos de la termodinámica, la entalpía se puede calcular mediante la determinación de los requisitos para la creación de un sistema de "nada"; requiere el trabajo mecánico, 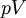 difiere, en base a la constancia de las condiciones presentes en la creación de la sistema termodinámico.
difiere, en base a la constancia de las condiciones presentes en la creación de la sistema termodinámico.
Energía interna, 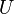 , Debe ser suministrado para eliminar las partículas de un circundante con el fin de dejar espacio para la creación de un sistema, proporcionando que las variables ambientales, tales como la presión (
, Debe ser suministrado para eliminar las partículas de un circundante con el fin de dejar espacio para la creación de un sistema, proporcionando que las variables ambientales, tales como la presión ( 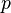 ) Permanecen constantes. Esta energía interna también incluye la energía necesaria para la activación y la ruptura de compuestos enlazados en especies gaseosas.
) Permanecen constantes. Esta energía interna también incluye la energía necesaria para la activación y la ruptura de compuestos enlazados en especies gaseosas.
Este proceso se calcula dentro de los cálculos de entalpía como 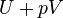 , Para etiquetar la cantidad de energía o trabajo necesario para "dejar de lado el espacio para" y "crear" el sistema; que describe el trabajo realizado tanto por la reacción o la formación de los sistemas, y los alrededores. Para los sistemas a presión constante, el cambio en la entalpía es el calor recibido por el sistema, más el trabajo no mecánica que se ha hecho.
, Para etiquetar la cantidad de energía o trabajo necesario para "dejar de lado el espacio para" y "crear" el sistema; que describe el trabajo realizado tanto por la reacción o la formación de los sistemas, y los alrededores. Para los sistemas a presión constante, el cambio en la entalpía es el calor recibido por el sistema, más el trabajo no mecánica que se ha hecho.
Por lo tanto, el cambio en la entalpía se puede diseñar o representado sin la necesidad de la mecánica de compresión o expansivo; para un sistema simple, con un número constante de partículas, la diferencia de entalpía es la cantidad máxima de energía térmica derivable de un proceso termodinámico en el que se mantiene constante la presión.
El término 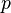
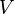 es el trabajo necesario para desplazar a la atmósfera circundante con el fin de desalojar el espacio para ser ocupado por el sistema.
es el trabajo necesario para desplazar a la atmósfera circundante con el fin de desalojar el espacio para ser ocupado por el sistema.
Relaciones
Como una extensión de la primera ley de la termodinámica , la entalpía puede estar relacionado con varias otras fórmulas termodinámicas. Al igual que con la definición original de la primera ley;
- Cuando, según lo definido por la ley;
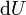 representa el incremento infinitesimal de la sistemática o energía interna.
representa el incremento infinitesimal de la sistemática o energía interna. 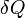 representa la cantidad infinitesimal de la energía atribuido o añadido al sistema.
representa la cantidad infinitesimal de la energía atribuido o añadido al sistema. 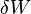 representa la cantidad infinitesimal de la energía actuado a cabo por el sistema en el entorno.
representa la cantidad infinitesimal de la energía actuado a cabo por el sistema en el entorno.
Como una expresión de la diferenciación, el valor de H se puede definir como
Donde
|
|
|
|
|
|
|
|
Para un proceso que no es reversible, la segunda ley de la termodinámica establece que el aumento de calor 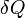 es inferior o igual al producto
es inferior o igual al producto 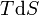 de la temperatura
de la temperatura 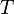 y el aumento de entropía
y el aumento de entropía 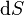 ; así
; así
Se ve que, si un proceso termodinámico es isobárica (es decir, ocurre a presión constante), entonces 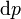 es cero y por lo tanto
es cero y por lo tanto
La diferencia de entalpía es la posible energía térmica máxima del sistema en un proceso isobárico. Esto explica por qué se llama a veces el contenido de calor. Es decir, la integral de 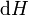 sobre cualquier isobara en el espacio de estado es el máximo alcanzable energía térmica del sistema.
sobre cualquier isobara en el espacio de estado es el máximo alcanzable energía térmica del sistema.
Si, además, la entropía se mantiene constante, así, es decir, 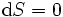 , La ecuación anterior se convierte en:
, La ecuación anterior se convierte en:
con la celebración de la igualdad en el equilibrio. Se ve que la entalpía de un sistema general disminuirá continuamente a su valor mínimo, que se mantiene en equilibrio.
En una forma más general, la primera ley describe la energía interna con términos adicionales que implican la potencial químico y el número de partículas de diversos tipos. La declaración diferencial para 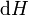 es entonces:
es entonces:
donde 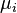 es el potencial químico de una partícula de tipo i, y
es el potencial químico de una partícula de tipo i, y 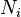 es el número de tales partículas. Se ve que, no sólo debe el
es el número de tales partículas. Se ve que, no sólo debe el 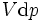 plazo se fija a cero, al exigir las presiones de los estados inicial y final para ser el mismo, pero el
plazo se fija a cero, al exigir las presiones de los estados inicial y final para ser el mismo, pero el 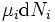 términos deben ser cero, así, al exigir que los números de partículas se mantienen sin cambios. Cualquier otra generalización añadirá aún más términos cuya extensa diferencial término se debe establecer en cero para que la interpretación de la entalpía de sostener.
términos deben ser cero, así, al exigir que los números de partículas se mantienen sin cambios. Cualquier otra generalización añadirá aún más términos cuya extensa diferencial término se debe establecer en cero para que la interpretación de la entalpía de sostener.
Los calores de reacción
La entalpía total de un sistema que no se puede medir directamente; el cambio de entalpía de una sistema se mide en su lugar. La variación de entalpía se define por la siguiente ecuación:
donde
- Δ H es el cambio de entalpía
- H final es la entalpía final del sistema, medida en julios. En una reacción química, H final es la entalpía de los productos.
- H inicial es la entalpía inicial del sistema, medida en julios. En una reacción química, H inicial es la entalpía de los reactivos.
Por un exotérmica reacción en constante la presión, el cambio del sistema de entalpía es igual a la energía liberada en la reacción, incluyendo la energía retenida en el sistema y perdido a través de la expansión en contra de sus alrededores. De una manera similar, para una reacción endotérmica, el cambio del sistema de entalpía es igual a la energía absorbida en la reacción, incluyendo la energía perdida por el sistema y ganado de la compresión de su entorno. Una forma relativamente fácil determinar si una reacción es exotérmica o endotérmica es determinar el signo de Δ H. Si Δ H es positivo, la reacción es endotérmica, es decir el calor es absorbido por el sistema debido a los productos de la reacción que tiene una entalpía mayor que los reactivos. Por otro lado, si Δ H es negativo, la reacción es exotérmica, es decir la disminución global de la entalpía se logra mediante la generación de calor.
Aunque entalpía es de uso común en la ingeniería y la ciencia, es imposible de medir directamente, como entalpía no tiene referencia (punto de referencia). Por lo tanto entalpía sólo con precisión puede ser utilizado en una sistema cerrado. Sin embargo, existen pocas aplicaciones del mundo real en el aislamiento cerrado, y es por esta razón por la que dos o más sistemas cerrados no se pueden comparar utilizando entalpía como base, aunque a veces esto se hace erróneamente.
Los sistemas abiertos
En termodinámica sistemas abiertos, la materia pueden fluir dentro y fuera de los límites del sistema. La primera ley de la termodinámica para sistemas abiertos establece: el aumento de la energía interna de un sistema es igual a la cantidad de energía añadida al sistema haciendo fluir la materia en y por calentamiento, menos la cantidad perdida por la materia que fluye hacia fuera y en la forma . del trabajo realizado por el sistema La primera ley para los sistemas abiertos está dado por:
donde U es en la energía interna media de entrar en el sistema y U a cabo es la energía interna media que sale del sistema

La región del espacio encerrado por los límites del sistema abiertos generalmente se llama una volumen de control, y que pueden o no corresponder a las paredes físicas. Si elegimos la forma del volumen de control de tal manera que todo el flujo dentro o fuera se produce perpendicular a su superficie, entonces el flujo de la materia en el sistema realiza trabajo como si se tratara de un pistón que empuja el líquido de la masa en el sistema, y el sistema realiza el trabajo sobre el desarrollo de la materia hacia fuera como si estuviera conduciendo un pistón de fluido. Hay, pues, dos tipos de trabajo realizado: el trabajo de flujo descrito anteriormente, que se realiza en el líquido (esto también se llama a menudo 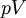 trabajo) y el eje de trabajo que puede realizarse en algún dispositivo mecánico.
trabajo) y el eje de trabajo que puede realizarse en algún dispositivo mecánico.
Estos dos tipos de trabajo se expresan en la ecuación:
Sustituyendo en la ecuación anterior para los rendimientos cv volumen de control:
La definición de entalpía, H, nos permite utilizar este potencial termodinámico para tener en cuenta tanto la energía interna y 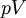 trabajar en los fluidos para sistemas abiertos:
trabajar en los fluidos para sistemas abiertos:
Durante la operación de estado estacionario de un dispositivo (ver turbina, bomba , y del motor), la expresión anterior puede ser igual a cero. Esto produce una expresión útil para el la generación de energía o la necesidad de estos dispositivos en la ausencia de reacciones químicas:
Esta expresión es descrito por el diagrama de arriba.
Cambios de entalpía estándar
Definiciones
Cambio de entalpía estándar de combustión
| " | Entalpía estándar de combustión se define como el cambio de entalpía observado en un sistema termodinámico constituyente cuando 1 mol de una sustancia se quema por completo debido a oxígeno bajo condiciones estándar. | " |
Cambio de entalpía estándar de hidrogenación
| " | Entalpía estándar de hidrogenación es el cambio de entalpía observado en un sistema termodinámico constituyente, cuando un mol de un compuesto insaturado que reacciona completamente con un exceso de hidrógeno bajo condiciones estándar para formar un compuesto saturado. | " |
Cambio de entalpía estándar de formación
| " | Cambio de entalpía estándar de formación se define como el cambio de entalpía observado en un sistema termodinámico constituyente cuando un mol de un compuesto se forma a partir de sus antecedentes elementales en condiciones estándar. | " |
Cambio de entalpía estándar de reacción
| " | Cambio de entalpía estándar de reacción (denotado H ° o H | " |
Entalpía Entramado
| " | Entalpía del enrejado es la entalpía requerida necesaria para separar un mol de un compuesto iónico en iones gaseosos separados a una distancia infinita aparte (es decir, sin fuerza de atracción) bajo condiciones estándar. . | " |
Un cambio de entalpía estándar común es la cambio de entalpía estándar de formación, que se ha determinado para un gran número de sustancias. El cambio de entalpía de una reacción en cualquier condición puede ser calculado, teniendo en cuenta la variación de entalpía estándar de formación de todos los reactivos y productos.
Otros tipos de cambio de entalpía estándar incluyen la combustión ( el cambio de entalpía estándar de combustión), de neutralización ( cambio estándar entalpía de neutralización), fusión / congelación ( cambio de entalpía estándar de fusión), vaporización / condensación ( el cambio de entalpía de vaporización estándar), atomización ( el cambio de entalpía estándar de atomización), mezcla ( el cambio de entalpía estándar de la mezcla), la disolución ( cambio de entalpía estándar de solución), y desnaturalización (cambio de entalpía estándar de desnaturalización).
Ejemplos: compuestos inorgánicos (a 25 ° C)
| Compuesto Químico | Fase (materia) | Fórmula química | Δ H f 0 en kJ / mol |
|---|---|---|---|
| El amoníaco (hidróxido de amonio) | aq | NH 3 (NH 4 OH) | -80.8 |
| Amoníaco | g | NH 3 | -46.1 |
| Cobre (II) sulfato | aq | CuSO4 | -769.98 |
| El carbonato de sodio | s | Na 2 CO 3 | -1131 |
| El cloruro de sodio (sal de mesa) | aq | NaCl | -407 |
| El cloruro de sodio (sal de mesa) | s | NaCl | -411.12 |
| El cloruro de sodio (sal de mesa) | l | NaCl | -385.92 |
| El cloruro de sodio (sal de mesa) | g | NaCl | -181.42 |
| Hidróxido de sodio | aq | NaOH | -469.6 |
| Hidróxido de sodio | s | NaOH | -426.7 |
| El nitrato de sodio | aq | NaNO3 | -446.2 |
| El nitrato de sodio | s | NaNO3 | -424.8 |
| Dioxido de azufre | g | SO 2 | -297 |
| Ácido sulfúrico | l | H 2 SO 4 | -814 |
| Sílice | s | SiO 2 | -911 |
| Dioxido de nitrogeno | g | NO 2 | 33 |
| El monóxido de nitrógeno | g | NO | 90 |
| Agua | l | H 2 O | -286 |
| Agua | g | H 2 O | -241.8 |
| Dióxido de carbono | g | CO 2 | -393.5 |
| Hidrógeno | g | H 2 | 0 |
| Flúor | g | F 2 | 0 |
| Cloro | g | Cl 2 | 0 |
| Bromo | l | Br 2 | 0 |
| Bromo | g | Br 2 | 31 |
| Yodo | s | I 2 | 0 |
| Yodo | g | I 2 | 62 |
| El sulfato de zinc | aq | ZnSO4 | -980.14 |
- (Estado: g = gaseoso; l = líquido; s = sólida; aq = acuoso)
Entalpía específica
La entalpía específica de una masa obrera es una propiedad de esa masa se utiliza en la termodinámica , definida como 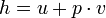 donde u es la energía interna específica, p es la presión, y v es el volumen específico. En otras palabras,
donde u es la energía interna específica, p es la presión, y v es el volumen específico. En otras palabras, 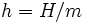 donde
donde 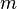 es la masa del sistema. La Unidad del SI para la entalpía específica es julios por kilogramo.
es la masa del sistema. La Unidad del SI para la entalpía específica es julios por kilogramo.

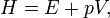
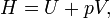
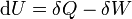
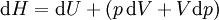
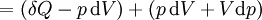
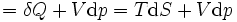
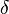 representa la diferencial inexacta.
representa la diferencial inexacta. 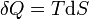 se añade la energía por calentamiento durante una proceso reversible,
se añade la energía por calentamiento durante una proceso reversible, 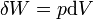 es el trabajo realizado por el sistema en un proceso reversible.
es el trabajo realizado por el sistema en un proceso reversible. 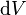 es una volumen infinitesimal
es una volumen infinitesimal