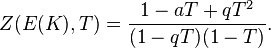Courbe elliptique
Renseignements généraux
SOS Enfants, qui se déroule près de 200 sos écoles dans le monde en développement, a organisé cette sélection. Cliquez ici pour en savoir plus sur le parrainage d'enfants.

En mathématiques , une courbe elliptique est une lisse, projective courbe algébrique genre une, sur laquelle il ya un point O spécifié. Une courbe elliptique est en fait un variété abélienne - autrement dit, il a une multiplication défini algébriquement, par rapport à laquelle il est (nécessairement commutatif ) groupe - O et sert d'élément d'identité. Souvent, la courbe elle-même, sans O spécifié, est appelé une courbe elliptique.
Toute courbe elliptique peut être écrit comme une courbe algébrique plane définie par une équation de la forme:
qui est non singulière; ce est son graphe n'a pas cuspides ou auto-intersections. (Quand le caractéristique du champ de coefficient est égal à 2 ou 3, l'équation ci-dessus ne est pas tout à fait assez général pour comprendre tous non singulière courbes cubes; voir ci-dessous pour une définition plus précise.) Le point O est en fait le " point à l'infini "dans le plan projectif.
Si y 2 = P (x), où P est un polynôme quelconque de degré trois pouces x répétées sans racines, on obtient alors une courbe plane non singulière de une genre, qui est donc également une courbe elliptique. Si P est de degré quatre et est quadratfrei cette équation décrit à nouveau une courbe plane d'une genre; cependant, il n'a pas le choix naturel de l'élément d'identité. Plus généralement, toute courbe algébrique du genre ci, par exemple à partir de l'intersection de deux quadriques intégrés dans l'espace tridimensionnel projective, est appelée une courbe elliptique, à condition qu'il ait au moins un point rationnel.
En utilisant la théorie de fonctions elliptiques, il peut être démontré que les courbes elliptiques définies sur les nombres complexes correspondent à plongements du tore dans le plan projectif complexe. Le tore est également un groupe abélien, et en fait, ce est également une correspondance groupe isomorphisme.
Les courbes elliptiques sont particulièrement importants dans la théorie des nombres , et constituent un domaine majeur de la recherche actuelle; par exemple, ils ont été utilisés dans la preuve, par Andrew Wiles (assisté par Richard Taylor), du dernier théorème de Fermat . Ils trouvent également des applications dans la cryptographie (voir l'article cryptographie à courbe elliptique) et factorisation entier.
Une courbe elliptique ne est pas une ellipse : voir intégrale elliptique de l'origine du terme. Topologiquement, une courbe elliptique est un tore .
Courbes elliptiques sur les nombres réels
Bien que la définition formelle d'une courbe elliptique est assez technique et nécessite une certaine expérience de la géométrie algébrique, il est possible de décrire quelques caractéristiques de courbes elliptiques sur les nombres réels en utilisant uniquement l'école secondaire l'algèbre et la géométrie .
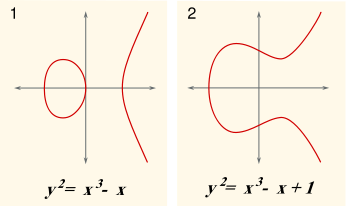
Dans ce contexte, une courbe elliptique est une courbe plane définie par une équation de la forme
où a et b sont des nombres réels. Ce type d'équation se appelle une équation de Weierstrass.
La définition de la courbe elliptique exige également que la courbe soit non singulière. Géométriquement, cela signifie que le graphe ne est pas cuspides, auto-intersections ou points isolés. Algébriquement, il se agit de calculer la discriminant
La courbe est non singulière si et seulement si le discriminant ne est pas égale à zéro. (Bien que le facteur ne semble pas pertinent ici -16, il se avère être pratique dans une étude plus poussée des courbes elliptiques.)
La (vraie) graphique d'une courbe non singulière a deux composantes si son discriminant est positif, et un composant se il est négatif. Par exemple, dans les graphiques présentés dans la figure à droite, le discriminant dans le premier cas est de 64, et dans le second cas est -368.
La loi de groupe
En ajoutant un "point à l'infini", on obtient la version projective de cette courbe. Si P et Q sont deux points de la courbe, on peut décrire de manière unique un troisième point qui est l'intersection de la courbe avec la ligne par P et Q. Si la ligne est tangente à la courbe en un point, alors ce point est compté deux fois; et si la ligne est parallèle à l'axe des y, nous définissons le troisième point que le point "à l'infini". Exactement une des conditions suivantes est vraie alors pour ne importe quelle paire de points d'une courbe elliptique.
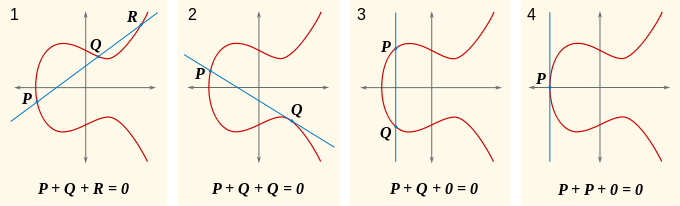
Il est alors possible d'introduire une opération de groupe , +, sur la courbe avec les propriétés suivantes: on considère le point à l'infini à 0, l'identité de groupe; et si une ligne droite coupe la courbe aux points P, Q et R, nous exigeons que P + Q + R = 0 dans le groupe. On peut vérifier que cela se transforme la courbe dans un groupe abélien, et donc dans un variété abélienne. On peut montrer que l'ensemble des K - points rationnels (y compris le point à l'infini) forme un sous-groupe de ce groupe. Si la courbe est représentée par E, puis ce sous-groupe est souvent écrit sous la forme E (K).
Le groupe ci-dessus peut être décrit algébriquement ainsi que géométriquement. Compte tenu de la courbe y = 2 x 3 - px - q sur le champ K (dont les caractéristique que nous supposons être ni deux, ni trois), et les points P = (x P, y P) et Q = (x Q, y Q) sur la courbe, supposent d'abord que x P x Q ≠. Soit s la pente de la ligne contenant P et Q; ce est à dire, s = (y P - y Q) / (x P - x Q). Depuis K est un champ, s est bien défini. Ensuite, nous pouvons définir R = P + Q = (R x, -y R) par
Si x P x = Q (troisième et quatrième volets ci-dessus), puis il ya deux options: si y = P - y Q, y compris le cas où y = y P Q = 0, alors la somme est définie comme 0; Ainsi, l'inverse de chaque point de la courbe se trouve en réfléchissant à travers la axe des x. Si y P y = Q ≠ 0 (deuxième volet), alors R = P + P = 2 P = (x R, Y R) est donnée par
Courbes elliptiques sur les nombres complexes

La formulation de courbes elliptiques comme l'incorporation d'un tore dans la plan projectif complexe découle naturellement un bien curieux Fonction elliptique de Weierstrass. Ces fonctions et leur dérivée première sont liés par la formule
Ici, G 2 et G 3 sont des constantes; 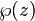 est la fonction elliptique de Weierstrass et
est la fonction elliptique de Weierstrass et 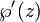 son dérivé. Il devrait être clair que cette relation est sous la forme d'une courbe elliptique (sur les nombres complexes ). Les fonctions de Weierstrass sont doublement périodique; autrement dit, ils sont périodiques par rapport à une treillis Λ; en substance, les fonctions de Weierstrass sont naturellement définis sur un tore T = C / Λ. Ce tore peut être incorporée dans le plan projectif complexe au moyen de la carte
son dérivé. Il devrait être clair que cette relation est sous la forme d'une courbe elliptique (sur les nombres complexes ). Les fonctions de Weierstrass sont doublement périodique; autrement dit, ils sont périodiques par rapport à une treillis Λ; en substance, les fonctions de Weierstrass sont naturellement définis sur un tore T = C / Λ. Ce tore peut être incorporée dans le plan projectif complexe au moyen de la carte
Cette carte est une groupe isomorphisme, portant la structure de groupe naturel du tore dans le plan projectif. Ce est aussi un isomorphisme de surfaces de Riemann , donc topologiquement, une courbe elliptique donnée ressemble à un tore. Si le treillis Λ est lié de par multiplication par un nombre non nul à un complexe c treillis Λ c, alors les courbes correspondantes sont isomorphes. classes d'isomorphisme de courbes elliptiques sont spécifiés par le j-invariant.
Les classes d'isomorphisme peuvent être comprises d'une manière plus simple ainsi. Les constantes g 2 et g 3, appelé le invariants modulaires, sont déterminés de façon unique par le réseau, qui est, par la structure du tore. Cependant, les nombres complexes de la forme champ de fractionnement pour les polynômes à coefficients réels, et ainsi de la courbe elliptique peut se écrire
On constate que
et
de sorte que le discriminant modulaire est
Ici, λ est parfois appelé le fonction lambda modulaire.
Notez que le uniformisation théorème implique que chaque compacte surface de Riemann de genre peut être représenté comme un tore.
Cela permet également une compréhension facile du points de torsion sur une courbe elliptique: si le treillis Λ est engendré par les périodes fondamentales ω 1 et ω 2, puis les n -torsion points sont les (classes d'équivalence de) points de la forme 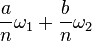 , Pour a et b des nombres entiers dans la gamme de 0 à n -1.
, Pour a et b des nombres entiers dans la gamme de 0 à n -1.
Sur les nombres complexes, chaque courbe elliptique a neuf les points d'inflexion. Chaque ligne à travers deux de ces points passe aussi par un troisième point d'inflexion; les neuf points et 12 lignes formées de cette manière forment une réalisation de la Configuration Hesse.
Courbes elliptiques sur les nombres rationnels
Une courbe E définie sur le corps des nombres rationnels est également défini sur le corps des nombres réels, donc la loi d'addition (de points avec coordonnées réelles) par la méthode de la tangente et sécant peut être appliqué à E. Les formules explicites montrer que la somme de deux points P et Q avec coordonnées rationnelles a pour coordonnées nouveau rationnels, depuis la ligne joignant P et Q a coefficients rationnels. De cette façon, on montre que l'ensemble des points rationnels de E forme un sous-groupe du groupe de points réels de E. Comme ce groupe, ce est un groupe abélien, ce est-à P + Q = Q + P.
La structure de points rationnels
Le résultat le plus important est que tous les points peuvent être construits par la méthode des tangentes et sécantes à partir d'un nombre fini de points. Plus précisément la Théorème de Mordell-Weil affirme que le groupe E (Q) est un fini généré groupe (commutatif). Par le théorème fondamental de groupes abéliens de type fini, il est donc une somme directe finie de copies de Z et des groupes cycliques finis.
La preuve de ce théorème repose sur deux ingrédients: d'abord, on montre que pour tout entier m> 1, le groupe quotient E (Q) / ME (Q) est fini (faible théorème de Mordell-Weil). D'autre part, l'introduction d'un fonction de la hauteur h sur les points rationnelle E (Q) défini par h (P 0) = 0 et h (P) = log max (| p |, | q |) si P (inégal au point à l'infini P 0) a en abscisse le nombre rationnel x = p / q (avec p et q premiers entre eux). Cette fonction de la hauteur h a la propriété que h (MP) se développe à peu près comme le carré de m. En outre, seulement un nombre fini de points rationnels avec hauteur inférieure à toute existent constante sur E.
La démonstration du théorème est donc une variante de la méthode de descente infinie et se appuie sur l'application répétée de Divisions euclidiennes sur E: soit P ∈ E (Q) soit un point rationnel sur la courbe, écrit P comme la somme 2 P 1 + Q 1 où Q 1 est un representant fixe de P dans E (Q) / 2 E (Q ), la hauteur de P 1 est d'environ 1/4 de celle de P (plus généralement, ne importe quel remplacement, par 2 m> 1, et 1/4 de 1 / m 2). Refaire la même chose avec P 1, ce est-à-dire P 1 = P 2 + Q 2 2, alors P = 2 P 2 Q 3 + 3, etc. exprime enfin P comme une combinaison linéaire de points intégrante Q i et des points dont hauteur est limitée par une constante fixe choisie à l'avance: par la faiblesse du théorème de Mordell-Weil et la seconde propriété de la fonction de la hauteur P est ainsi exprimé en combinaison linéaire intégrante d'un nombre fini de points fixes.
Jusqu'à présent, le théorème ne est pas efficace car il n'y a pas de procédure générale connue pour déterminer les representants de E (Q) / ME (Q).
Le rang de E (Q), ce est le nombre de copies de Z à E (Q) ou, de façon équivalente, le nombre de points indépendants d'ordre infini, est appelé le rang de E. Le Conjecture de Birch et Swinnerton-Dyer est préoccupé par déterminer le rang. On conjecture qu'il peut être arbitrairement grand, même si seuls exemples avec relativement faible rang sont connus. La courbe elliptique avec le plus grand rang exactement connu est
- y 2 + xy = x 3 − 26 175 960 092 705 884 096 311 701 787 701 203 903 556 438 969 515 x + 51 069 381 476 131 486 489 742 177 100 373 772 089 779 103 253 890 567 848 326 .
Il est de rang 18, trouvée par Noam Elkies en 2006. Les courbes de rang au moins 28 sont connus, mais leur rang ne est pas exactement connue.
En ce qui concerne les groupes constituant la sous-groupe de torsion E (Q), ce qui suit est connu le sous-groupe de torsion de E (Q) est l'un des 15 groupes suivants (un théorème en raison de Barry Mazur): Z / N Z pour N = 1, 2, ..., 10, ou 12, ou Z / 2 Z × Z / 2 N Z avec N = 1, 2, 3, 4. Exemples pour tous les cas sont connus . En outre, les courbes elliptiques dont Mordell-Weil sur Q groupes ont les mêmes groupes de torsion appartiennent à une famille paramétrée.
La conjecture de Birch et Swinnerton-Dyer
La Conjecture de Birch et Swinnerton-Dyer (BSD) est l'un des problèmes du millénaire de la Clay Mathematics Institute. La conjecture se appuie sur des objets d'analyse et de calcul définies par la courbe elliptique en question.
Sur le côté analytique, un ingrédient important est une fonction d'une variable complexe, L, la Hasse-Weil fonction zeta de E sur Q. Cette fonction est une variante de la Fonction zêta de Riemann et Fonctions L de Dirichlet. Il est défini comme une Euler produit, avec un seul facteur pour chaque nombre premier p.
Pour une courbe E sur Q donnée par une équation minimale
à coefficients entiers de un i, réduisant les coefficients modulo p définit une courbe elliptique sur la champ fini F p (sauf pour un nombre fini de nombres premiers p, où la courbe présente une diminution singularité et donc ne parvient pas à être elliptique, auquel cas E est dit des mauvaise réduction en p).
La fonction zêta d'une courbe elliptique sur un corps fini F p est, dans un certain sens, un la fonction de génération de l'information de l'assemblage du nombre de points de E avec des valeurs dans le fini extensions de terrain de F p, F p n. Il est donné,
La somme intérieur de l'exponentielle ressemble le développement du logarithme et, en fait, la fonction zêta ainsi défini est un fonction rationnelle:
La fonction zêta de Hasse-Weil de E sur Q est alors défini par la collecte de ces informations, pour tous les nombres premiers p. Elle est définie par
où ε (p) = 1 si E a bonne réduction en p et 0 sinon (dans ce cas, un P est défini différemment que ci-dessus).
Ce produit converge pour 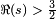 seulement. La conjecture de Hasse affirme que le L admet une -fonction prolongement analytique à l'ensemble du plan complexe et satisfait une équation fonctionnelle relative, pour tout s, L (E, S) à L (E, 2 s). En 1999, ce est révélé être une conséquence de la preuve de la conjecture de Shimura-Taniyama-Weil, qui affirme que toute courbe elliptique sur Q est un courbe modulaire, ce qui implique que son -fonction L est la L -fonction d'un forme modulaire dont le prolongement analytique est connue.
seulement. La conjecture de Hasse affirme que le L admet une -fonction prolongement analytique à l'ensemble du plan complexe et satisfait une équation fonctionnelle relative, pour tout s, L (E, S) à L (E, 2 s). En 1999, ce est révélé être une conséquence de la preuve de la conjecture de Shimura-Taniyama-Weil, qui affirme que toute courbe elliptique sur Q est un courbe modulaire, ce qui implique que son -fonction L est la L -fonction d'un forme modulaire dont le prolongement analytique est connue.
On peut donc parler des valeurs de L (E, s) à ne importe quel nombre complexe s. La conjecture de Birch-Swinnerton-Dyer concerne l'arithmétique de la courbe pour le comportement de son L -fonction s = 1. Plus précisément, il affirme que l'ordre de la L -fonction en s = 1 est égal au rang de E et prédit la terme principal de la série de Laurent L (E, s) à ce point en termes de plusieurs quantités attachés à la courbe elliptique.
Tout comme le Hypothèse de Riemann, cette conjecture a de multiples conséquences, y compris les deux suivantes:
- Soit n un impair sans carré entier. En supposant que la conjecture de Birch et Swinnerton-Dyer, n est la zone d'un triangle rectangle avec des longueurs rationnels secondaires (une nombre congruent) si et seulement si le nombre de triplets de nombres entiers (x, y, z) vérifiant
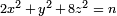 est le double du nombre de triplets satisfaisant
est le double du nombre de triplets satisfaisant  . Cette déclaration, en raison de Tunnell, est liée au fait que n est un nombre congruent si et seulement si la courbe elliptique
. Cette déclaration, en raison de Tunnell, est liée au fait que n est un nombre congruent si et seulement si la courbe elliptique 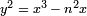 a un point d'ordre infini (donc, en vertu de la conjecture de Birch et Swinnerton-Dyer, son L -fonction a un zéro à 1) rationnelle. L'intérêt de cette déclaration est que la condition est facilement vérifiée.
a un point d'ordre infini (donc, en vertu de la conjecture de Birch et Swinnerton-Dyer, son L -fonction a un zéro à 1) rationnelle. L'intérêt de cette déclaration est que la condition est facilement vérifiée. - Dans une autre direction, certaines méthodes d'analyse permettent une estimation de l'ordre de zéro au centre de la bande critique de familles de L -functions. Admettant la conjecture de BSD, ces estimations correspondent à l'information sur le rang des familles de courbes elliptiques en question. Par exemple ,: supposons que la hypothèse de Riemann généralisée et la conjecture de BSD, le rang moyen de courbes donnée par
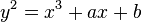 est inférieur à 2.
est inférieur à 2.
Le théorème de modularité et son application à le dernier théorème de Fermat
Le théorème de modularité, autrefois connue comme la conjecture de Shimura-Taniyama-Weil, affirme que toute courbe elliptique E sur Q est un courbe modulaire, ce est-à-dire, sa fonction zêta de Hasse-Weil est le L -fonction d'un forme modulaire de poids 2 et de niveau N, où N est le conducteur de E (un nombre entier divisible par les mêmes nombres premiers que le discriminant de E, Δ (E).) En d'autres termes, si, par 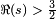 , On écrit la L -fonction sous la forme
, On écrit la L -fonction sous la forme
l'expression 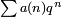 , Où q = exp (iz 2π) définit un modulaire parabolique newform de poids 2 et de niveau N. Pour nombres premiers ℓ pas divisant N, le coefficient
, Où q = exp (iz 2π) définit un modulaire parabolique newform de poids 2 et de niveau N. Pour nombres premiers ℓ pas divisant N, le coefficient 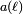 de la forme est égal à ℓ - le nombre de solutions de l'équation minimale de la courbe de ℓ modulo.
de la forme est égal à ℓ - le nombre de solutions de l'équation minimale de la courbe de ℓ modulo.
Par exemple, pour la courbe elliptique 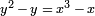 de discriminant (et chef d'orchestre) 37, est associée la forme
de discriminant (et chef d'orchestre) 37, est associée la forme 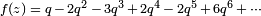 Où
Où 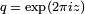 . Pour nombres premiers ℓ distinctes de 37 ans, on peut vérifier la propriété sur les coefficients. Ainsi, pour ℓ = 3, les solutions de l'équation modulo 3 sont (0, 0), (0, 1), (2, 0), (1, 0), (1, 1), (2, 1) , au fur et
. Pour nombres premiers ℓ distinctes de 37 ans, on peut vérifier la propriété sur les coefficients. Ainsi, pour ℓ = 3, les solutions de l'équation modulo 3 sont (0, 0), (0, 1), (2, 0), (1, 0), (1, 1), (2, 1) , au fur et 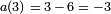 .
.
La conjecture, qui remonte aux années cinquante, a été complètement montré en 1999 en utilisant des idées de Andrew Wiles, qui a déjà prouvé en 1994 pour une grande famille de courbes elliptiques.
Il existe plusieurs formulations de la conjecture. En démontrant qu'elles sont équivalentes est difficile et a été un sujet principal de la théorie des nombres dans la seconde moitié du 20e siècle. La modularité d'une courbe elliptique E du conducteur N peut également être exprimé en disant qu'il ya un non constante carte rationnelle définie sur Q, de la courbe modulaire 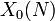 à E. En particulier, les points de E peuvent être paramétrées par fonctions modulaires.
à E. En particulier, les points de E peuvent être paramétrées par fonctions modulaires.
Par exemple, une paramétrisation modulaire de la courbe  est donnée par
est donnée par
où, comme précédemment, q = exp (iz 2π). Les fonctions x (z) et y (z) sont modulaires de poids 0 et le niveau 37; en d'autres termes ils sont méromorphe, définie sur la demi-plan supérieur  et satisfaire
et satisfaire 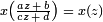 et de même pour y (z) pour tout entier a, b, c, d avec ad - bc = 1 et 37 | c.
et de même pour y (z) pour tout entier a, b, c, d avec ad - bc = 1 et 37 | c.
Une autre formulation dépend de la comparaison de représentations de Galois fixés d'une part à courbes elliptiques, et d'autre part à des formes modulaires. Cette dernière formulation a été utilisée dans la démonstration de la conjecture. Traiter avec le niveau des formes (et la connexion au conducteur de la courbe) est particulièrement délicate.
L'application la plus spectaculaire de la conjecture est la preuve de théorème de Fermat (FLT). Supposons que pour un nombre premier p> 5, l'équation de Fermat
a une solution avec des entiers non nuls, donc un contre-exemple à la FLT. Ensuite, la courbe elliptique
de discriminant 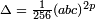 ne peut pas être modulaire. Ainsi, la preuve de la conjecture de Shimura-Taniyama-Weil pour cette famille de courbes elliptiques (appelées courbes Hellegouarch-Frey) implique la FLT. La preuve du lien entre ces deux déclarations, basée sur une idée de Gerhard Frey (1985), est difficile et technique. Il a été créé par Kenneth Ribet en 1987.
ne peut pas être modulaire. Ainsi, la preuve de la conjecture de Shimura-Taniyama-Weil pour cette famille de courbes elliptiques (appelées courbes Hellegouarch-Frey) implique la FLT. La preuve du lien entre ces deux déclarations, basée sur une idée de Gerhard Frey (1985), est difficile et technique. Il a été créé par Kenneth Ribet en 1987.
Points entiers
Cet article concerne des points P = (x, y) de E tel que x est un nombre entier. Le théorème suivant est due à CL Siegel: l'ensemble des points P = (x, y) de E (Q) de telle sorte que x est entier est fini. Ce théorème peut être généralisée à points dont les coordonnées x a un dénominateur divisible que par un ensemble fini de nombres premiers fixe.
Le théorème peut être formulée de manière efficace. Par exemple, si l'équation de Weierstrass de E coefficients entiers limitées par une constante H, les coordonnées (x, y) d'un point de E à la fois x et y satisfaire entier:
Par exemple, l'équation 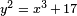 a huit solutions intégrales avec y> 0:
a huit solutions intégrales avec y> 0:
- (X, y) = (1,4), (2,3), (2,5), (4,9), (8,23), (43 282) (52 375), (5 234, 378 661).
Comme autre exemple, L'équation de Ljunggren, une courbe dont la forme est Weierstrass y 2 = x 3-2 x, n'a que quatre solutions avec y ≥ 0:
- (X, y) = (0,0), (-1,1), (2, 2), (338,6214).
Généralisation aux champs numériques
Beaucoup des résultats précédents restent valables lorsque le champ de la définition de E est un champ de numéro, ce est-à-dire, un ensemble fini extension de domaine de Q. En particulier, le groupe E (K) de K des points -rationnels d'une courbe elliptique E définie sur K est de type fini, qui généralise le théorème de Mordell-Weil-dessus. Un théorème de Loïc Merel montre que pour un nombre entier j donné, il existe ( à isomorphisme près) qu'un nombre fini de groupes qui peuvent se produire que les groupes de torsion de E (K) pour une courbe elliptique définie sur un champ de nombre K de degré d. Plus précisément, il existe un nombre B (d) telle que, pour toute courbe elliptique E définie sur un corps de nombres K de degré d, un point quelconque de E (K) de torsion est de commander inférieur à B (d). Le théorème est efficace: pour d> 1, si un point de torsion est d'ordre p, avec p premier, alors 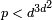 .
.
Quant aux points entiers, le théorème de Siegel généralise à la suivante: soit E une courbe elliptique définie sur un corps de nombres K, x et y coordonne le Weierstrass. Ensuite, les points de E (K) dont le -Coordonner x est dans la anneau des entiers O K est fini.
Les propriétés de la fonction zêta de Hasse-Weil et la Conjecture de Birch et Swinnerton-Dyer peuvent également être étendus à cette situation plus générale.
Courbes elliptiques sur un champ général
Les courbes elliptiques peuvent être définis sur toute corps K; la définition formelle d'une courbe elliptique est une courbe algébrique projective non singulière sur K avec genre 1 avec un point donné défini sur K.
Si le caractéristique de K ne est ni deux, ni trois, alors chaque courbe elliptique sur K peut être écrit sous la forme
où p et q sont des éléments de K tel que le droit polynôme côté x 3 - px - q ne possède pas de racines doubles. Si la caractéristique est 2 ou 3, puis plusieurs termes doivent être conservés: en caractéristique 3, l'équation la plus générale l'est de la forme
pour des constantes arbitraires 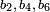 tels que le polynôme sur le côté droit a des racines distinctes (la notation est choisie pour des raisons historiques). Dans caractéristique 2, même autant ne est pas possible, et l'équation la plus générale l'est
tels que le polynôme sur le côté droit a des racines distinctes (la notation est choisie pour des raisons historiques). Dans caractéristique 2, même autant ne est pas possible, et l'équation la plus générale l'est
à condition que la variété qu'elle définit est non singulière. Si caractéristique ne était pas un obstacle, chaque équation se réduit à la précédente par une modification appropriée de variables.
On prend généralement la courbe comme étant l'ensemble de tous les points (x, y) qui satisfont à l'équation ci-dessus et de telle sorte que x et y sont des éléments de la clôture algébrique de K. Points de la courbe dont coordonne deux appartiennent à K sont appelés les points K -rationnels.
Isogénie
Soient E et D soit courbes elliptiques sur un corps k. Une isogénie entre E et D est un finie morphisme f: E → D variétés qui préserve points de base (en d'autres termes, le point sur les cartes E donnée à celle sur D).
Les deux courbes sont appelés isogène se il existe une isogénie entre elles. Il se agit d'une relation d'équivalence , symétrie étant due à l'existence de la double isogénie. Chaque isogénie est un algébrique homomorphisme et induit donc homomorphismes des groupes des courbes elliptiques pour les points k -Évaluées.
Les courbes elliptiques sur les corps finis
 .
. Soit K = F q le corps fini à q éléments et E une courbe elliptique définie sur K. Alors que le précise nombre de points rationnels d'une courbe elliptique E sur K est en général assez difficile à calculer, Le théorème de Hasse sur les courbes elliptiques nous donne, y compris le point à l'infini, l'estimation suivante:
En d'autres termes, le nombre de points de la courbe croît à peu près comme le nombre d'éléments dans le domaine. Ce fait peut être compris et prouvé à l'aide d'une théorie générale; voir fonction zeta locale, Cohomologie étale.

 .
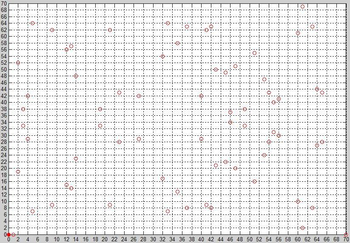
. L'ensemble des points E (F q) est un groupe abélien fini. Il est toujours cyclique ou le produit de deux groupes cycliques. Par exemple, la courbe définie par
sur F 71 a 72 points (71 points affines y compris (0,0) et une point à l'infini) sur ce domaine, dont le périmètre est donnée par Z / 2 Z × Z / Z 36. Le nombre de points sur une courbe spécifique peut être calculée avec L'algorithme de Schoof.
Etudier la courbe sur la extensions de champ de F q est facilitée par l'introduction de la fonction zêta locale de E sur F q, défini par une série de génération (voir également ci-dessus)
où le corps K n est le (unique) extension de K = F q de degré n (ce est-à  ). La fonction zeta est une fonction rationnelle dans T. Il est un nombre entier de telle sorte que
). La fonction zeta est une fonction rationnelle dans T. Il est un nombre entier de telle sorte que
Par ailleurs,
avec des nombres complexes α, β de valeur absolue  . Ce résultat est un cas particulier de la Conjectures de Weil. Par exemple, la fonction zêta de
. Ce résultat est un cas particulier de la Conjectures de Weil. Par exemple, la fonction zêta de 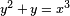 sur le corps F 2 est donnée par
sur le corps F 2 est donnée par 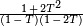 depuis la courbe a
depuis la courbe a 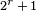 (
( 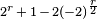 ) Points sur
) Points sur 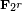 si r est impair (même, respectivement).
si r est impair (même, respectivement).
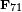 .
. Le Sato-Tate conjecture est une déclaration sur la façon dont le terme d'erreur 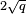 dans le théorème de Hasse varie avec les différents nombres premiers q, si vous prenez une courbe elliptique E sur Q et réduisez q modulo. Il a été prouvé (pour presque tous ces courbes) en 2006 en raison des résultats de Taylor, Harris et Shepherd-Barron, et dit que les termes d'erreur sont équiréparties.
dans le théorème de Hasse varie avec les différents nombres premiers q, si vous prenez une courbe elliptique E sur Q et réduisez q modulo. Il a été prouvé (pour presque tous ces courbes) en 2006 en raison des résultats de Taylor, Harris et Shepherd-Barron, et dit que les termes d'erreur sont équiréparties.
Les courbes elliptiques sur les corps finis sont notamment appliquées dans la cryptographie et de la factorisation de grands nombres entiers. Ces algorithmes font souvent usage de la structure de groupe sur les points de E. Algorithmes qui sont applicables à des groupes généraux, par exemple le groupe des éléments inversibles dans des domaines finis, 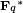 , Peut ainsi être appliquée sur le groupe de points sur une courbe elliptique. Par exemple, le logarithme discret est un tel algorithme. L'intérêt est que le choix d'une courbe elliptique permet une plus grande souplesse que de choisir q (et donc le groupe d'unités de F q). En outre, la structure de groupe de courbes elliptiques est généralement plus complexe.
, Peut ainsi être appliquée sur le groupe de points sur une courbe elliptique. Par exemple, le logarithme discret est un tel algorithme. L'intérêt est que le choix d'une courbe elliptique permet une plus grande souplesse que de choisir q (et donc le groupe d'unités de F q). En outre, la structure de groupe de courbes elliptiques est généralement plus complexe.
Algorithmes qui utilisent les courbes elliptiques
Les courbes elliptiques sur les corps finis sont utilisés dans certains cryptographiques applications ainsi que pour factorisation entier. Typiquement, l'idée générale de ces applications est connu qu'un algorithme qui rend l'utilisation de certains groupes finis est réécrit pour utiliser les groupes de points rationnels des courbes elliptiques. Pour plus Voir aussi:
- Cryptographie à courbe elliptique
- Elliptic Curve DSA
- Lenstra courbe elliptique factorisation
- Courbe elliptique primalité proving
Représentations alternatives de courbes elliptiques
- Courbe de Hesse
- Courbe Edwards
- Courbe Twisted
- Courbe Twisted Hesse
- Courbe Twisted Edwards
- Courbe Doche-Icart-Kohel orientée jumelage
- Courbe Doche-Icart-Kohel Triplement orienté
- Courbe jacobienne
- Courbe Montgomery

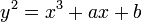
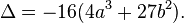
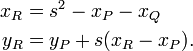
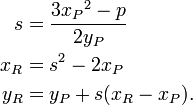
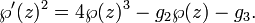
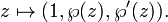
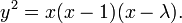
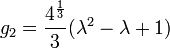
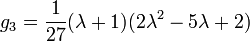
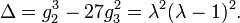
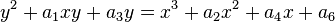
![Z (E (\ mathbf {F} _p)) = \ exp \ left (\ sum \ mathrm {carte} \ left [E ({\ mathbf F} _ {p ^ n}) \ right] \ frac {T ^ n} {n} \ right).](../../images/1230/123094.png)
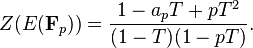
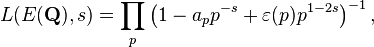
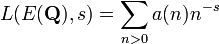
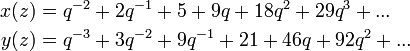
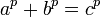
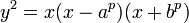
![\ Max (| x |, | y |) <\ exp \ left (\ left [10 ^ 6H \ right] ^ {{10} ^ 6} \ right).](../../images/1231/123117.png)

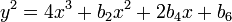
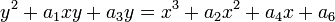
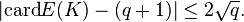
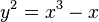
![Z (E (K), T) \ equiv \ exp \ left (\ sum_ {n = 1} ^ {\ infty} \ mathrm {carte} \ left [E (K_N) \ right] {T ^ n \ n plus } \ right)](../../images/1231/123137.png)