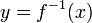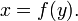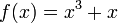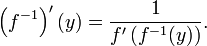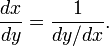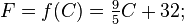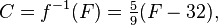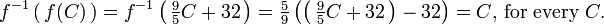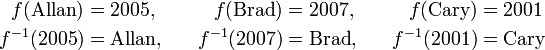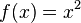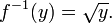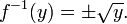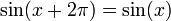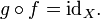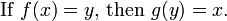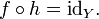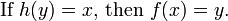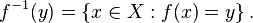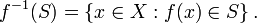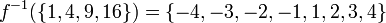Fonction inverse
Renseignements généraux
SOS Enfants, un organisme de bienfaisance de l'éducation , a organisé cette sélection. Voir http://www.soschildren.org/sponsor-a-child pour connaître le parrainage d'enfants.

En mathématiques , une fonction inverse est une fonction qui annule une autre fonction: Si une entrée x dans la fonction f produit une sortie y, alors y mettre dans la fonction inverse g produit la sortie x, et vice versa. ce est à dire f (x) = y, et g (y) = x. Plus directement, g (f (x)) = x, ce qui signifie g (x) composé avec f (x) x laisse inchangé.
Une fonction f qui a un inverse est appelé inversible; la fonction inverse est alors uniquement déterminée par f et est désignée par f -1 (lecture inverse f, à ne pas confondre avec exponentiation ).
Définitions
Le mot inverse est lié au mot inverti signifie inverser, tourner à l'envers, de faire le contraire.
| Chercher inverse dans Wiktionary, le dictionnaire libre. |
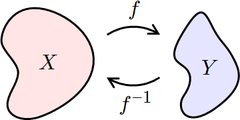
Au lieu de considérer les inverses pour les entrées et sorties individuelles, on peut penser à la fonction que l'envoi de l'ensemble des entrées, le domaine, à un ensemble de sorties, les gamme. Soit f une fonction dont le domaine est l' ensemble X, et dont la portée est l'ensemble Y. Alors f est inversible se il existe une fonction g avec le domaine Y et la gamme X, avec la propriété:
Si f est inversible, la fonction g est unique; en d'autres termes, il ya exactement une fonction g satisfaire cette propriété (ni plus, ni moins). Cette fonction g est alors appelé l'inverse de f, et généralement notée f -1.
En d'autres termes, une fonction est inversible si et seulement si son relation est une fonction inverse de la plage Y, dans ce cas, la relation inverse est la fonction inverse.
Toutes les fonctions ne ont pas l'inverse. Pour que cette règle soit applicable, chaque élément y ∈ Y doit correspondre à pas plus d'un x ∈ X; une fonction f avec cette propriété est appelée un-à-un, ou des informations de préservation, ou un injection.
opérations inverses qui conduisent à inverser fonctions Exemple:
Opérations inverses sont à l'opposé des fonctions directes de variation. Fonction directe de variation sont basées sur la multiplication; y = kx. L'opération inverse de la multiplication est division et une fonction de variation inverse est y = k / x.
Exemple: quadrature et les fonctions de la racine carrée
La fonction f (x) = x 2 peut ou non être inversible, en fonction du domaine.
Si le domaine est les nombres réels, puis chaque élément de Y correspondrait à deux éléments différents dans X (± x), et donc f ne serait pas inversible. Plus précisément, la carrée de x ne est pas inversible, car il est impossible de déduire à partir de sa sortie le signe de son entrée. Une telle fonction est appelée non injectif ou information perdante. Notez que ni la racine carrée ni la place principale racine fonction est l'inverse de x 2 parce que la première ne est pas rendements à valeur unique, et le second - x lorsque x est négatif.
Si le domaine est constitué des numéros non-négatives, alors la fonction est injective et inversible.
Inverses en mathématiques supérieur
La définition donnée ci-dessus est communément adoptée en théorie des ensembles et de calcul . En mathématiques supérieures, la notation
signifie "f est un des éléments de cartographie de la fonction d'un ensemble X à des éléments d'un ensemble Y". La source, X, est appelé le domaine de f, et la cible, Y, est appelé le codomaine. Le codomain contient la gamme de f comme un sous-ensemble , et est considéré comme faisant partie de la définition de f.
Lors de l'utilisation codomaines, l'inverse d'une fonction f: X → Y est requis d'avoir domaine Y et X codomaine. Pour l'inverse, à définir sur l'ensemble de Y, chaque élément de Y doit se situer dans la plage de la fonction f. Une fonction avec cette propriété est appelée sur ou un surjection. Ainsi, une fonction avec un ensemble d'arrivée est inversible si et seulement si elle est à la fois injective (one-to-one) et surjective (sur). Une telle fonction est appelée une à une correspondance ou d'un bijection, et a la propriété que chaque élément y ∈ Y correspond à exactement un élément x ∈ X.
Inverses et la composition
Si f est une fonction inversible avec le domaine X et Y plage, puis
Cette instruction est équivalente à la première des définitions mentionnées ci-dessus de l'inverse, et il devient équivalente à la seconde définition si Y coïncide avec le codomaine de f. Utilisation de la composition de fonctions , nous pouvons réécrire cette instruction comme suit:
où id est le X fonction identité sur l'ensemble X; ce est la fonction X qui laisse inchangée. En la théorie des catégories, cette déclaration est utilisée comme la définition d'un inverse morphisme.
Si nous pensons de la composition comme une sorte de multiplication des fonctions, cette identité dit que l'inverse d'une fonction est analogue à un inverse multiplicatif. Ceci explique l'origine de la notation f -1.
Remarque sur la notation
La notation des exposants pour un inverses peut parfois être confondue avec d'autres utilisations des exposants, en particulier lorsqu'il se agit de trigonométrique et fonctions hyperboliques. Pour éviter cette confusion, les notations f [-1] ou avec le "-1" au-dessus du f sont parfois utilisés.
Il est important de réaliser que f -1 (x) ne est pas la même que f (x) -1. En f -1 (x), l'exposant "-1" ne est pas un exposant . Une notation similaire est utilisé pour fonctions répétées. Par exemple, f 2 représente deux itérations de la fonction f; si f (x) = x 2 - 1, f 2 (x) = f (f (x)) = f (x 2 - 1) = (x 2 - 1) 2 - 1, ce qui simplifie à 4 x - 2 x 2. Dans symboles:
Dans le calcul, f (n), avec entre parenthèses, désigne le n-ième dérivée d'une fonction f. Par exemple:
Dans la trigonométrie , pour des raisons historiques, sin 2 X ne signifie généralement la place du péché x:
Toutefois, l'expression sin -1 x habituellement ne représentent pas l'inverse multiplicatif de pécher x, mais l'inverse de la fonction sinus appliquée à x (en fait un inverse partielle ; voir ci-dessous). Pour éviter toute confusion, un fonction trigonométrique inverse est souvent indiqué par le préfixe "arc". Par exemple, l'inverse de la fonction sinus est typiquement appelé le fonction arcsinus, écrit arcsin, qui est, comme le péché, classiquement désigné dans caractères romains et non dans italiques (Notez que les bibliothèques de logiciels de fonctions mathématiques utilisent souvent le nom asin):
La fonction (sin x) -1 est l'inverse multiplicatif au sinus, et est appelée la cosécante . Il est généralement csc x notée:
Fonctions hyperboliques se comportent de manière similaire, en utilisant le préfixe "ar", comme dans arsinh pour la fonction inverse de sinh, et pour x csch l'inverse multiplicatif de sinh x.
Propriétés
Unicité
Si une fonction inverse existe pour une fonction donnée f, il est unique: il doit être le relation inverse.
Symétrie
Il existe une symétrie entre une fonction et son inverse. Plus précisément, si f est une fonction inversible avec le domaine X et Y gamme, alors son inverse f -1 a domaine Y et la gamme X, et l'inverse de f -1 est la fonction f originale. En symboles, pour f une fonction avec le domaine X et Y gamme, et g une fonction avec le domaine Y et la gamme X:
Cela découle de la connexion entre la fonction inverse et relation inverse, parce inversion de relations est un involution.
Cette déclaration est une conséquence évidente de la déduction que pour f soit inversible, il doit être injective (première définition de l'inverse) ou bijective (deuxième définition). La propriété de symétrie peut être exprimée de façon concise par la formule suivante:
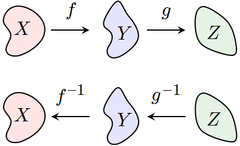
L'inverse d'une composition de fonctions est donnée par la formule
Notez que l'ordre de g et f ont été inversée; pour annuler f suivi par g, nous devons d'abord défaire g puis défaire f.
Par exemple, soit f (x) = x 3 et laisser g (x) = x + 5 Puis la composition g o f est la fonction qui multiplie par trois premiers, puis ajoute cinq.:
Pour inverser ce processus, nous devons d'abord soustraire cinq, puis diviser par trois:
Ce est la composition (f -1 o g -1) (y).
Auto-inverses
Si X est un ensemble, alors le fonction identité sur X est son propre inverse:
Plus généralement, une fonction f: X → X est égale à sa propre inverse si et seulement si la composition f o f est égal à X id. Une telle fonction est appelée involution.
Inverses en calcul
Une variable calcul est principalement concernée par les fonctions qui correspondent nombres réels aux nombres réels. De telles fonctions sont souvent définis par des formules telles que:
Une fonction f des nombres réels pour les nombres réels possède un inverse aussi longtemps que ce est l'un-à-un, la valeur de x à-dire aussi longtemps que le graphique de y = f (x) présente, pour chaque valeur y possible que l'une correspondante , et passe ainsi le test de ligne horizontale.
Le tableau suivant présente plusieurs fonctions standard et leurs inverses:
La fonction f (x) F inverse -1 (y) Remarques x + a y - un a - x a - y mx y / m m ≠ 0 1 / x 1 / y x, y ≠ 0 x 2 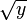
x, y ≥ 0 uniquement x 3 ![\ Sqrt [3] {y}](../../images/2472/247204.png)
aucune restriction sur x et y x p y 1 / p (ce est à dire ![\ Sqrt [p] {y}](../../images/2472/247205.png) )
) x, y ≥ 0, en général, p ≠ 0 e x ln y y> 0 un x connecter un y y> 0 et a> 0 fonctions trigonométriques fonctions trigonométriques inverses diverses restrictions (voir tableau ci-dessous)
Formule pour l'inverse
Une approche pour trouver une formule de F-1, se il existe, est de résoudre l'équation y = f (x) pour x. Par exemple, si f est la fonction
alors nous devons résoudre l'équation y = (x 2 + 8) 3 pour x:
Ainsi, la fonction inverse F -1 est donnée par la formule
Parfois, l'inverse d'une fonction ne peut être exprimée par une formule avec un nombre fini de termes. Par exemple, si f est la fonction
f est un-à-un, et possède donc une fonction inverse f-1. La formule pour cette inverse a un nombre infini de termes:
Le graphique de l'inverse
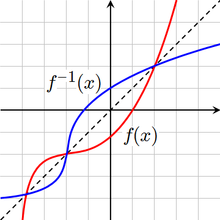
Si f et f-1 sont inverses, alors le graphe de la fonction
est la même que celle du graphique de l'équation
Elle est identique à l'équation y = f (x) qui définit le graphe de f, à l'exception que les rôles de x et y ont été inversés. Ainsi, le graphe de f -1 peut être obtenu à partir de la courbe de f en commutant les positions des axes x et y. Ceci est équivalent à reflétant le graphique dans la droite y = x.
Inverses et dérivés
Un fonction continue f est un-à-un (et donc inversible) si et seulement si elle est soit strictement augmentant ou en diminuant (sans locale maxima ou minima). Par exemple, la fonction
est inversible, car le dérivé de f '(x) = x 3 2 + 1 est toujours positif.
Si la fonction f est différentiables, alors l'inverse f -1 seront différentiables tant que f '(x) ≠ 0. Le dérivé de l'inverse est donnée par la fonction inverse théorème:
Si l'on pose x = f -1 (y), la formule ci-dessus peut être écrite
Ce résultat découle du règle de la chaîne (voir l'article sur fonctions inverses et la différenciation).
Le théorème des fonctions inverse peut être généralisé aux fonctions de plusieurs variables. Plus précisément, une fonction différentiable f: R n → R n est inversible dans un voisinage d'un point p tant que le Jacobienne matrice de f en p est inversible. Dans ce cas, le jacobien de f à f -1 (p) est la matrice inverse du jacobien de f à la p.
Exemples du monde réel
Par exemple, soit f la fonction qui convertit une température en degrés Celsius de la température en degrés Fahrenheit:
alors sa fonction inverse convertit degrés Fahrenheit en degrés Celsius:
depuis
Ou, supposons f attribue à chaque enfant dans une famille de son année de naissance. Une fonction inverse serait sortie qui l'enfant est né dans une année donnée. Cependant, si la famille a des jumeaux ou des triplés (), puis la sortie ne peut pas être connu lorsque l'entrée est l'année de naissance commune. En outre, si une année est donnée dans laquelle aucun enfant ne est né, puis un enfant ne peut pas être nommé. Mais si chaque enfant est né dans une année distincte, et si on se limite aux trois années au cours desquelles un enfant est né, puis nous avons une fonction inverse. Par exemple,
Généralisations
Inverses partiels

Même si une fonction f ne est pas un à un, il peut être possible de définir un inverse de f partielle en limitant le domaine. Par exemple, la fonction
ne est pas une à une, étant donné que x 2 = (- x) 2. Cependant, la fonction devient un-à-un, si nous limitons au domaine x ≥ 0, auquel cas
(Si nous limitons lieu au domaine x ≤ 0, alors l'inverse est le négatif de la racine carrée de y.) Sinon, il ne est pas nécessaire de restreindre le domaine si nous sommes satisfaits de l'inverse étant un fonction à valeurs multiples:
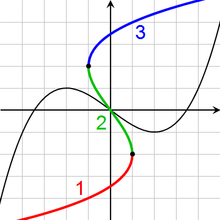
Parfois, cela inverse valeurs multiples est appelé la pleine inverse de f, et les parties (tels que √ x et x -√) sont appelées branches. La branche la plus importante d'une fonction à valeurs multiples (par exemple la racine carrée positive) est appelée la branche principale, et sa valeur à y se appelle la valeur principale de f -1 (y).
Pour une fonction continue sur la droite réelle, une branche est nécessaire entre chaque paire de extrema locaux. Par exemple, l'inverse d'une fonction cubique avec un maximum local et un minimum local a trois branches (voir l'image à droite).

Ces considérations sont particulièrement importantes pour définir les inverses des fonctions trigonométriques . Par exemple, le fonction sinus ne est pas un-à-un, depuis
pour tous les réels x (et plus généralement sin (x + 2π n) = sin (x) pour tout entier n). Cependant, le sinus est une-à-une dans l'intervalle [- π / 2, π / 2], et l'inverse partiel correspondant est appelé le arcsinus. Ceci est considéré comme la branche principale du sinus inverse, de sorte que la valeur principale du sinus inverse est toujours comprise entre - π / 2 et π / 2. Le tableau suivant décrit la branche principale de chaque fonction trigonométrique inverse:
fonction Gamme de d'habitude valeur principale sin -1 - Π / 2 ≤ sin -1 (x) ≤ π / 2 cos -1 0 ≤ -1 cos (x) ≤ π tan -1 - Π / 2 <tan -1 (x) <π / 2 lit -1 0 <lit -1 (x) <π sec -1 0 ≤ s -1 (x) ≤ π csc -1 - Π / 2 ≤ csc -1 (x) ≤ π / 2
Gauche et droite inverses
Si f: X → Y, un inverse à gauche pour f (ou rétraction de f) est une fonction g: Y → X tel que
Ce est, la fonction g satisfait à la règle
Ainsi, g doit être égale à l'inverse de f sur la gamme de f, mais peut prendre toutes les valeurs pour les éléments de Y ne sont pas dans la gamme. Une fonction f avec un inverse à gauche est nécessairement injective. En mathématiques classiques, chaque fonction injective f a nécessairement une inverse à gauche; toutefois, cela peut échouer dans mathématiques constructives. Par exemple, un inverse à gauche de l'inclusion {0,1} → R des deux-ensemble d'éléments dans les reals viole en donnant une indécomposabilité rétraction de la ligne réelle à l'ensemble {0,1}.
Un inverse à droite pour f (ou section de f) est une fonction h: Y → X tel que
Ce est, la fonction h satisfait à la règle
Ainsi, h (y) peut être ne importe lequel des éléments de X qui correspondent aux sous f y. Une fonction f a un inverse à droite si et seulement si il est surjective (si la construction d'une telle inverse en général exige que le axiome du choix).
L'inverse qui est à la fois à gauche et inverse à droite doivent être uniques. De même, si g est un inverse à gauche pour f, g peut ou ne peut pas être un inverse à droite pour f; et si g est un inverse à droite pour f, g ne est pas nécessairement un inverse à gauche pour f. Par exemple soit f: R → [0, ∞) désignent la carte quadrature, tel que f (x) = x 2 pour tout x dans R, et laissez g: [0, ∞) → R désigner la carte de la racine carrée, tels que g (x) = √x pour tous x≥0. Alors f (g (x)) = x pour tout x dans [0, ∞); ce est-g est un inverse à droite à f. Cependant, g est pas un inverse de f gauche, étant donné que, par exemple, g (f (-1)) = 1 ≠ -1.
Préimages
Si f: X → Y est une fonction (pas nécessairement inversible), l'image réciproque (ou une image inverse) d'un élément y ∈ Y est l'ensemble de tous les éléments de X qui correspondent à y:
L'image réciproque de y peut être considéré comme le image de y sous le (valeurs multiples) complète inverse de la fonction f.
De même, si S est tout sous-ensemble de Y, l'image réciproque de S est l'ensemble des éléments de X qui correspondent à S:
Par exemple, prenez une fonction f: R → R, où f: x ↦ x 2. Cette fonction ne est pas inversible pour les raisons évoquées ci-dessus . Pourtant préimages peuvent être définies pour les sous-ensembles de l'ensemble d'arrivée:
L'image réciproque d'un seul élément y ∈ Y - un singleton ensemble {y} - est parfois appelé le fibres de y. Lorsque Y est l'ensemble des nombres réels, il est courant de se référer à f -1 (y) en tant que niveau réglé.

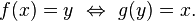
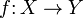

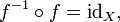
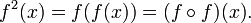
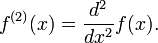
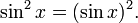
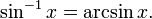
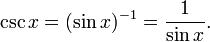
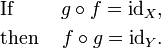
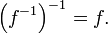
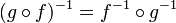
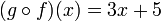
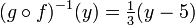
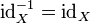
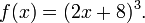
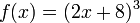
![\ Begin {align} y = & (2x + 8) ^ 3 \\ \ sqrt [3] {y} & = 2x + 8 \\ \ sqrt [3] {y} - 8 & = 2x \\ \ {dfrac \ sqrt [3] {y} - 8} {2} & = x. \ End {align}](../../images/2472/247207.png)
![f ^ {- 1} (y) = \ dfrac {\ sqrt [3] {y} - 8} {2}. \, \!](../../images/2472/247208.png)
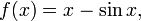
![f ^ {- 1} (y) = \ displaystyle \ sum_ {n = 1} ^ {\ infty} {! \ frac {y ^ {\ frac {n} {3}}} {n}} \ lim_ {\ theta \ 0} \ left (\ frac {\ mathrm {d} ^ {\, n-1}} {\ mathrm {d} \ theta ^ {\, n-1}} \ left (\ frac {\ theta } {\ sqrt [3] {\ theta - \ sin (\ theta)}} ^ n \ right) \ right)](../../images/2472/247210.png)