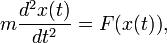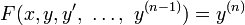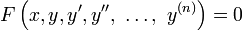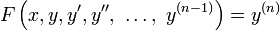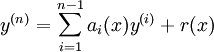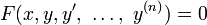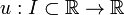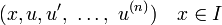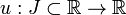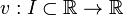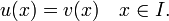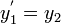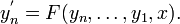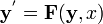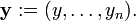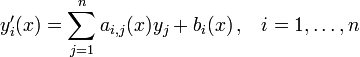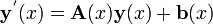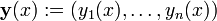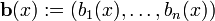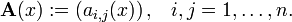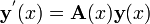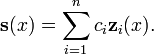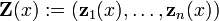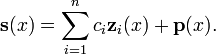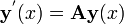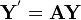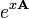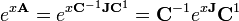Conteúdo verificado

Equação diferencial ordinária

Assuntos Relacionados: Matemática

Sobre este escolas selecção Wikipedia

Este conteúdo da Wikipedia foi escolhida pela SOS Children para adequação nas escolas de todo o mundo. Patrocinar uma criança para fazer uma diferença real.

Em matemática , uma equação diferencial ordinária (ou ODE) é uma relação que contém funções de apenas um variável independente, e um ou mais dos seus derivados no que diz respeito a essa variável.

Um exemplo simples é a segunda lei de Newton de movimento, o que conduz à equação diferencial

m \ frac {d ^ 2 x (t)} {dt ^ 2} = F (x (t)), \,

para o movimento de uma partícula de massa m. Em geral, a força F depende da posição da partícula x (t) no instante t, e, assim, a função desconhecida x (t) aparece em ambos os lados da equação diferencial, como está indicado na notação F (x (t )).

Equações diferenciais ordinárias estão a ser distinguido de equações diferenciais parciais onde existem diversas variáveis independentes que envolvam derivadas parciais.

Equações diferenciais ordinárias surgir em muitos contextos diferentes, incluindo geometria, mecânica, astronomia e modelagem população. Muitos matemáticos famosos estudaram equações diferenciais e contribuiu para o campo, incluindo Newton , Leibniz , o Família Bernoulli, Riccati, Clairaut, d'Alembert e Euler .

Muito trabalho tem sido dedicado à solução de equações diferenciais ordinárias. No caso em que a equação é linear, que pode ser resolvido por métodos analíticos. Infelizmente, a maioria das equações diferenciais interessantes são não-linear e, com poucas exceções, não pode ser resolvido exatamente. Soluções aproximadas são chegou a usar aproximações de computador (veja numéricas de equações diferenciais ordinárias).

O trajetória de um projétil lançado a partir de um canhão segue uma curva determinada por uma equação diferencial comum, que é derivada a partir da segunda lei de Newton.

Definições

Equação diferencial ordinária

Seja Y uma função desconhecida

y: \ mathbb {R} \ to \ mathbb {R}

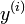em x com y ^ {(i)} o i-ésimo derivado de y, em seguida, uma função

F (x, y, y ', \ \ pontos, \ y ^ {(n-1)}) = Y ^ {(n)}

é chamado de uma equação diferencial ordinária (ODE) de ordem n. Para funções vetoriais valorizado

y: \ mathbb {R} \ to \ mathbb {R} ^ m

F é chamado de um sistema de equações diferenciais ordinárias de dimensão m.

Quando uma equação diferencial de ordem n tem a forma

F \ esquerda (x, y, y ', y' ', \ \ pontos, \ y ^ {(n)} \ direita) = 0

ele é chamado de uma equação diferencial implícita enquanto que a forma

F \ esquerda (x, y, y ', y' ', \ \ pontos, \ y ^ {(n-1)} \ direita) = Y ^ {(n)}

é chamado de uma equação diferencial explícito.

Uma equação diferencial não dependendo de x é chamado autônoma.

Uma equação diferencial é dito ser linear se F pode ser escrito como um combinação linear dos derivados de Y

y ^ {(n)} = \ sum_ {i = 1} ^ {n-1} a_i (x) y ^ {(i)} + r (x)

com um i (x) e R (x) funções contínuas em x. A função r (x) é chamado o termo fonte; se R (x) = 0, então a equação diferencial linear é chamada homogénea, caso contrário, é chamado não homogénea ou não homogénea.

Soluções

Dada uma equação diferencial

F (x, y, y ', \ \ pontos, \ y ^ {(n)}) = 0

uma função

u: I \ subset \ mathbb {R} \ to \ mathbb {R}

é chamada solução ou curva integral para F, se L é n -times diferenciável em que, M é definido por todas

(X, u, u ', \ \ pontos, \ u ^ {(n)}) \ quad x \ in I

e

F (x, u, u ', \ \ pontos, \ u ^ {(n)}) = 0 \ quad x \ in I.

Dadas duas soluções

u: J \ subset \ mathbb {R} \ to \ mathbb {R}

e

v: I \ subset \ mathbb {R} \ to \ mathbb {R}

u é chamado de uma extensão de v se eu ⊂ J e

u (x) = v (x) \ quad x \ in I. \,

Uma solução que não tem extensão é chamado de uma solução global.

A solução geral de uma equação n -ésima ordem é uma solução contendo 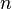n variáveis arbitrárias, o que corresponde a n constantes de integração. Uma solução particular é derivado a partir da solução geral, definindo as constantes para valores particulares, muitas vezes escolhido para cumprir SET 'iniciais ou de contorno Condições'. A solução singular é uma solução que não pode ser derivada a partir da solução geral.

Exemplos

Redução de um sistema de primeira ordem

Qualquer equação diferencial de ordem n pode ser escrito como um sistema de equações diferenciais de primeira ordem n. Dada uma equação diferencial ordinária de ordem n explícita e dimensão 1,

F \ esquerda (x, y, y ', y' ', \ \ pontos, \ y ^ {(n-1)} \ direita) = Y ^ {(n)}

que definem uma nova família de funções desconhecidas

Y_n: = y ^ {(n-1)} \.!

Podemos, então, reescrever a equação diferencial original como um sistema de equações diferenciais com a ordem 1 e dimensão n.

y_1 ^ '= y_2
\ vdots
Y_n ^ '= F (Y_n, \ pontos, y_1, x).

que pode ser escrito de forma concisa na notação de vetores como

\ Mathbf {y} ^ '= \ mathbf {F} (\ mathbf {y}, x)

com

\ Mathbf {y}: = (y, \ ldots, Y_n).

Lineares de equações diferenciais ordinárias

Uma classe particular bem compreendido de equações diferenciais são equações diferenciais lineares. Sempre podemos reduzir a uma equação diferencial linear explícita de qualquer forma a um sistema de equações diferenciais de ordem 1

y_i '(x) = \ sum_ {j = 1} n ^ a_ {i, j} (x) + y_j b_i (x) \, \ mathrm {,} \ quad i = 1, \ ldots, n

que podemos escrever de forma concisa usando a notação de vetores como

\ Mathbf {y ^} '(x) = \ mathbf {A} (x) \ mathbf {y} (x) + \ mathbf {b} (x)

com

\ Mathbf {y} (x): = (y_1 (X), \ ldots, Y_n (x))
\ Mathbf {b} (x): = (b_1 (X), \ ldots, b_n (x))
\ Mathbf {A} (x): = (a_ {i, j} (x)) \, \ mathrm {,} \ quad i, j = 1, \ ldots, n.

Equações homogéneas

O conjunto de soluções para um sistema de equações diferenciais lineares homogéneas de ordem 1 e dimensão n

\ Mathbf {y ^} '(x) = \ mathbf {A} (x) \ mathbf {y} (x)

forma um n-dimensional de espaço vectorial . Dada uma base para este espaço vetorial 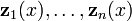\ Mathbf {z} _1 (X), \ ldots, \ mathbf {z} _N (x) , O que é chamado um sistema fundamentais, todas as soluções 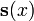\ Mathbf {s} (x) pode ser escrita como

\ Mathbf {s} (x) = \ sum_ {i = 1} ^ {n} C_I \ mathbf {z} _i (x).

A matriz n × n

\ Mathbf {Z} (x): = (\ mathbf {z} _1 (X), \ ldots, \ mathbf {z} _N (x))

é chamado matriz fundamental. Em geral, não há método para construir explicitamente um sistema fundamental, mas se uma solução é conhecida D'Alembert redução pode ser utilizado para reduzir a dimensão da equação diferencial por um.

Equações não homogéneas

O conjunto de soluções para um sistema de equações diferenciais lineares não homogéneas de ordem 1 e dimensão n

\ Mathbf {y ^} '(x) = \ mathbf {A} (x) \ mathbf {y} (x) + \ mathbf {b} (x)

pode ser construído por encontrar o sistema fundamentais 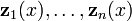\ Mathbf {z} _1 (X), \ ldots, \ mathbf {z} _N (x) para a equação homogênea correspondente e uma solução particular 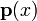\ Mathbf {p} (x) com a equação não homogénea. Cada solução 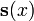\ Mathbf {s} (x) a equação não homogénea pode então ser escrito como

\ Mathbf {s} (x) = \ sum_ {i = 1} ^ {n} C_I \ mathbf {z} _i (x) + \ mathbf {p} (x).

Uma solução particular para a equação não homogénea pode ser encontrada pela método dos coeficientes indeterminados ou o método da variação de parâmetros.

Sistemas fundamentais para equações homogêneas com coeficientes constantes

Para um sistema de equações diferenciais lineares de coeficientes constantes homogéneos

\ Mathbf {y} ^ '(x) = \ mathbf {A} \ mathbf {y} (x)

podemos construir explicitamente um sistema fundamentais. O sistema pode ser escrita como uma equação diferencial matriz

\ Mathbf {Y} ^ '= \ mathbf {A} \ mathbf {Y}

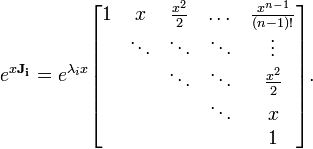
com solução como um matriz exponencial

e ^ {x \ mathbf {A}}

que é uma matriz fundamental para a equação diferencial de origem. Para calcular esta expressão que explicitamente primeiro transformar uma em Jordan forma normal

e ^ {x \ mathbf {A}} = e ^ {x \ mathbf {C} ^ {- 1} \ mathbf {J} \ mathbf {C} ^ {1}} = \ mathbf {C} ^ {- 1 } e ^ {x \ mathbf {J}} \ mathbf {C} ^ {1}

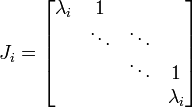
e em seguida avaliar a Blocos Jordânia

J_i = \ begin {bmatrix} \ lambda_i & 1 & \; & \; \\ \; & \ Ddots & \ ddots & \; \\ \; & \; & \ & 1 ddots \\ \; & \; & \; & \ Lambda_i \ end {bmatrix}

de J separadamente como

e ^ {x \ mathbf {J_i}} = e ^ {\ lambda_i x} \ begin {} 1 & bmatrix x & \ frac {x ^ 2} {2} & \ dots & \ frac {x ^ {n-1 }} {(n-1)} \\ \!; & \ Ddots & \ ddots & \ ddots & \ vdots \\ \; & \; & \ Ddots & \ ddots & \ frac {x ^ 2} {2} \\ \; & \; & \; & \ Ddots & x \\ \; & \; & \; & \; & 1 \ end {} bmatrix.

Teorias da ODEs

Soluções singulares

A teoria da soluções singulares de equações diferenciais ordinárias e parciais era um assunto de pesquisa a partir do momento de Leibniz, mas só a partir de meados do século XIX é que ele receberá atenção especial. Um trabalho valioso, mas pouco conhecido sobre o tema é o da Houtain (1854). Darboux (a partir de 1873) era um líder na teoria e na interpretação geométrica destas soluções abriu um campo que foi trabalhado por vários escritores, nomeadamente Casorati e Cayley. Para este último é devido (1872) a teoria de soluções singulares de equações diferenciais de primeira ordem como aceitou cerca de 1900.

Redução de Quadraturas

A tentativa primitiva em lidar com equações diferenciais tinha em vista uma redução de quadraturas. Tal como tinha sido a esperança de algebristas do século XVIII para encontrar um método para resolver a equação geral da 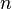n th grau, portanto, foi a esperança de analistas de encontrar um método geral para a integração de qualquer equação diferencial. Gauss (1799) mostrou, no entanto, que a equação diferencial atende suas limitações muito em breve, a menos que os números complexos são introduzidos. Daí analistas começaram a substituir o estudo de funções, abrindo assim um campo novo e fértil. Cauchy foi o primeiro a apreciar a importância deste ponto de vista. Depois disso, a questão real era para ser, não se uma solução é possível por meio de funções conhecidas ou seus integrais, mas se uma determinada equação diferencial é suficiente para a definição de uma função da variável ou variáveis independentes, e em caso afirmativo, quais são os propriedades características desta função.

Teoria fuchsianas

Duas memórias de Fuchs (Crelle, 1866, 1868), inspirou uma nova abordagem, posteriormente elaborado por Thomé e Frobenius. Collet foi um colaborador proeminente no início de 1869, embora o seu método para integrar um sistema não-linear foi comunicada ao Bertrand em 1868. Clebsch (1873) atacou a teoria em linhas paralelas aos seguidos na sua teoria da Integrais abelianos. À medida que o último pode ser classificada de acordo com as propriedades da curva fundamental que permanece inalterada sob uma transformação racional, de modo Clebsch proposto classificar as funções transcendentes definidos pelas equações diferenciais de acordo com as propriedades invariantes das superfícies correspondentes f = 0 sob uma racional -to-ona transformações.

A teoria de Lie

De 1870 O trabalho de Lie colocar a teoria das equações diferenciais em uma base mais satisfatória. Ele mostrou que as teorias de integração dos matemáticos mais velhos pode, pela introdução de que agora são chamados Grupos de Lie, ser submetido a uma fonte comum; e que as equações diferenciais ordinárias que admitir o mesmo transformações infinitesimais apresentar dificuldades comparáveis de integração. Ele também enfatizou o tema da transformações de contato (Berührungstransformationen).

Teoria de Sturm-Liouville

Teoria de Sturm-Liouville é um método geral para a resolução de equações lineares de segunda ordem com coeficientes variáveis.

Retirado de " http://en.wikipedia.org/w/index.php?title=Ordinary_differential_equation&oldid=198824413 "