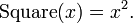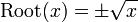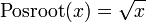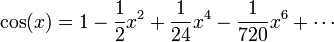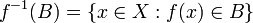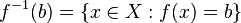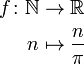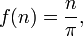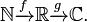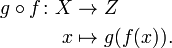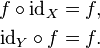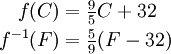Função (matemática)
Fundo para as escolas Wikipédia
Esta seleção é feita para as escolas de caridade infantil leia mais . Um link rápido para o patrocínio criança é http://www.sponsor-a-child.org.uk/
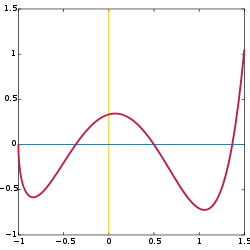
![\ Begin {align} & \ scriptstyle f \ colon [-1,1.5] \ para [-1,1.5] \\ & \ textstyle x \ mapsto \ frac {(4x ^ 3-6x ^ 2 + 1) \ sqrt { x + 1}} {3-x} \ end {align}](../../images/121/12113.png)
O matemático conceito de uma função expressa dependência entre duas quantidades, uma das quais é dado (o variável independente, o argumento da função, ou o seu "input") e outra produzida (a variável dependente, o valor da função, ou "saída"). Uma função associa uma única saída para cada elemento de entrada recebida a partir de um fixo definido, tal como os números reais .
Há muitas maneiras para dar uma função: por um fórmula , por uma trama ou gráfico, por um algoritmo que calcula que, por uma descrição de suas propriedades. Por vezes, uma função é descrita através da sua relação com outras funções (ver, por exemplo, da função inversa ). Em disciplinas aplicadas, as funções são freqüentemente especificada por suas tabelas de valores ou por uma fórmula. Nem todos os tipos de descrição pode ser dado para cada função possível, e deve-se fazer uma distinção clara entre a função em si e múltiplas formas de apresentação ou visualizando-o.
Uma ideia de enorme importância em toda a matemática é composição de funções : Se z é uma função de y e y é uma função de x, então Z é uma função de x. Podemos descrever informalmente por dizer que a função composto é obtido usando a saída da primeira função que a entrada do segundo. Esta característica das funções que os diferencia dos outros construtos matemáticos, como números ou figuras, e fornece a teoria de funções com a sua estrutura mais poderosa.
Introdução
Funções desempenhar um papel fundamental em todas as áreas da matemática, bem como em outras ciências e engenharia. No entanto, a intuição referentes a funções, notação, e até mesmo o próprio significado do termo "função" varia entre os campos. Mais áreas abstratos de matemática, tais como a teoria dos conjuntos , considere os tipos muito gerais de funções, que não podem ser especificados por uma regra concreta e não são regidas por quaisquer princípios familiares. A propriedade característica de uma função no sentido mais abstracto é que ele se relaciona exatamente uma saída para cada uma das suas entradas admissíveis. Estas funções não precisam de números e pode envolver, por exemplo, associar cada um de um conjunto de palavras com as suas próprias primeiras letras.
Funções em álgebra são geralmente expresso em termos de operações algébricas. Funções estudados em análise , tal como a função exponencial , podem ter propriedades adicionais que derivam de continuidade do espaço, mas, no caso mais geral, não pode ser definido por uma única fórmula. Funções analíticas em análise complexa pode ser definida bastante concreta através da sua expansões em série. Por outro lado, em lambda cálculo, a função é um conceito primitivo, em vez de ser definida em termos da teoria dos conjuntos. Os termos e transformação mapeamento são muitas vezes sinônimo de função. Em alguns contextos, no entanto, eles diferem ligeiramente. No primeiro caso, a transformação termo geralmente se aplica a funções cujas entradas e saídas são elementos do mesmo conjunto ou estrutura mais geral. Assim, falamos de transformações lineares de um espaço vetorial em si mesmo e de simetria transformações de um objeto geométrico ou um padrão. No segundo caso, usado para descrever conjuntos cuja natureza é arbitrária, o termo mapeamento é o conceito mais geral da função.
Funções matemáticas são denotados por letras frequentemente, e a notação padrão para a produção de uma função f, com a entrada x é f (x). A função pode ser definida apenas para determinados insumos, bem como a recolha de todas as entradas aceitáveis da função é chamada de domínio. O conjunto de todas as saídas resultantes chama-se a faixa da função. No entanto, em muitos campos, é também importante para especificar o codomain de uma função, que contém o intervalo, mas não precisa ser igual a ele. A distinção entre gama e codomain nos permite perguntar se os dois acontecerá a ser iguais, o que, em casos especiais pode ser uma questão de algum interesse matemático.
Por exemplo, a expressão do ácido (x) = x 2 descreve um ƒ função de uma variável x, que, dependendo do contexto, pode ser um número inteiro , um verdadeiro ou complexo número ou mesmo um elemento de um grupo . Vamos especificar que x é um número inteiro; refere-se, em seguida, esta função cada entrada, x, com uma única saída, x 2, obtido a partir de x por quadratura. Assim, a entrada de 3 está relacionado com a saída de 9, a entrada 1 para a saída de 1, e a entrada de -2 para a produção de 4, e escrever metílico do ácido (3) = 9, ƒ (1) = 1, ƒ (-2) = 4. Uma vez que cada número inteiro pode ser quadrado, o domínio desta função consiste de todos os números inteiros, enquanto a sua gama é o conjunto de quadrados perfeitos. Se escolher números inteiros como o codomain assim, descobrimos que muitos números, tais como 2, 3, e 6, estão no codomain mas não o intervalo.
É uma prática habitual em matemática para introduzir funções com nomes temporários, como ƒ; no parágrafo seguinte que pode definir f (x) = 1 x 2, e em seguida, f (3) = 7. Quando um nome para que a função não é necessária, muitas vezes a forma y = x 2 é usada.
Se usarmos uma função muitas vezes, podemos dar-lhe um nome mais permanente como, por exemplo,
A propriedade essencial de uma função que é para cada entrada deve haver uma saída única. Assim, por exemplo, a fórmula
não define uma função de uma variável real positivo, porque ele atribui duas saídas para cada número: as raízes quadradas de 3 e 9 estão -3. Para fazer com que a raiz quadrada de uma função, é preciso especificar quais raiz quadrada para escolher. A definição
para qualquer entrada positiva escolhe a raiz quadrada positiva como uma saída.
Como mencionado acima, uma função não necessita de envolver números. A título de exemplos, considere a função que associa a cada palavra sua primeira carta ou a função que associa a cada triângulo sua área.
Definições
Porque as funções são usadas em muitas áreas da matemática, e, de muitas formas diferentes, nenhuma definição de função tem sido universalmente adotada. Algumas definições são elementares, enquanto outros usam linguagem técnica que pode obscurecer a noção intuitiva. No entanto, a idéia essencial é a mesma em toda definição.
Uma definição elementar que é
- Uma função é dada por uma expressão aritmética que descreve como um número depende de outro.
Um exemplo de tal função é y = 5 x 16 -20 x 3 x 5, onde o valor de y depende do valor de x. Isto é inteiramente satisfatória para partes da matemática elementar, mas é muito desajeitado e restritiva para mais áreas avançadas. Por exemplo, o co-seno função utilizada em trigonometria não pode ser gravado nesta forma; o melhor que podemos fazer é uma série infinita,
Dito isto, se estamos dispostos a aceitar série como um sentido mais amplo de "expressão aritmética", temos uma definição que serviu matemática razoavelmente bem por centenas de anos.
Eventualmente, a transformação gradual de "cálculo" intuitiva em "análise" formal trouxe a necessidade de uma definição mais ampla. A ênfase mudou de como uma função foi apresentado - como uma fórmula ou regra - a um conceito mais abstrato. Parte da nova fundação foi o uso de conjuntos , de modo que as funções foram não mais restrita a números. Assim, podemos dizer que
- A ƒ função de um conjunto X para um conjunto Y associa a cada elemento x em X um elemento y = f (x) em Y.
Note-se que X e Y não necessitam de ser conjuntos diferentes; é possível ter uma função de um conjunto para si. Embora seja possível interpretar o termo "associados" nesta definição com uma regra concreta para a associação, é essencial ir além das que a restrição. Por exemplo, às vezes podemos provar que uma função com certas propriedades existe, ainda não ser capaz de dar qualquer regra explícita para a associação. Na verdade, em alguns casos é impossível dar uma regra explícita um produzindo y específica para cada x, apesar de uma tal função existe. No contexto de funções definidas sobre conjuntos arbitrárias, não é ainda clara a forma como a expressão "regra expressa" deve ser interpretado.
Como funções de assumir novos papéis e encontrar novos usos, a relação da função para os conjuntos requer mais precisão. Talvez cada elemento em Y está associado com algum x, talvez não. Em algumas partes da matemática, incluindo teoria da recursão e análise funcional, é conveniente permitir que os valores de x sem associação (neste caso, o termo função parcial é frequentemente utilizado). Para ser capaz de discutir tais distinções, muitos autores dividir uma função em três partes, cada uma de um conjunto:
- A função ƒ é uma tripla ordenada de conjuntos (F, X, Y), com restrições, onde
- F (gráfico) é um conjunto de pares ordenados (x, y),
- X (a origem) contém todos os primeiros elementos de F e talvez mais, e
- Y (o alvo) contém todos os segundos elementos de F e talvez mais.
As restrições mais comuns são de que cada X pares F com apenas um y, e que X é apenas o conjunto de primeiros elementos da F e nada mais.
Quando não existem restrições sobre F, falamos de uma relação entre X e Y, em vez de uma função. A relação é "de valor único" quando a primeira restrição contém: (x, y 1) ∈ F e (x, y 2) ∈ F em conjunto implica Y 1 = Y 2. Relações que não são valorizados único são chamados às vezes funções de valor múltiplo. A relação é "total" quando uma segunda restrição detém: se x ∈ X, em seguida, (x, y) ∈ F por algum y. Assim, podemos também dizer que
- Uma função de X para Y é um valor único relação, total entre X e Y.
A faixa de M, e de f, é o conjunto de todos os segundos elementos de F; é muitas vezes indicada por rng ƒ. O domínio de F é o conjunto de todos os primeiros elementos de F; muitas vezes é indicado por dom ƒ. Há duas definições comuns para o domínio de ƒ alguns autores definem como o domínio do F, enquanto outros o definem como a fonte de F.
O alvo Y de ƒ também é chamado de codomain de ƒ, denotado por bacalhau ƒ; e a gama de ƒ também é chamada de imagem de f, denotado por im ƒ. O ƒ notação: X → Y indica que ƒ é uma função com domínio X e Y codomain.
Alguns autores omitir a origem eo destino de dados desnecessários. Com efeito, dado apenas o gráfico F, pode-se construir um triplo adequado, tomando dom F para ser a fonte e rng F a ser o alvo; isto faz com que automaticamente F a ser total. No entanto, a maioria dos autores em matemática avançada preferem o maior poder de expressão proporcionada pelo triplo, especialmente a distinção entre ele permite alcance e codomain.
Aliás, os pares e triplos ordenados que usamos não são distintos dos conjuntos; podemos facilmente representá-los no prazo de teoria dos conjuntos. Por exemplo, pode-se utilizar {{x}, {x, y}} para o par (x, y). Em seguida, para um triplo (x, y, z) que pode utilizar o par ((x, y), z). Uma construção importante é a Produto cartesiano dos conjuntos X e Y, denotado por X × Y, que é o conjunto de todos os possíveis pares ordenados (x, y) com x ∈ X e y ∈ Y. Nós também podemos construir o conjunto de todas as funções possíveis de conjunto X para definir Y, que denotamos por um ou outro [X → Y] ou Y X.
Temos agora uma enorme flexibilidade. Usando pares para X podemos tratar, digamos, subtração de inteiros como uma função, sub: Z × Z → Z. Usando pares para Y podemos desenhar uma curva planar usando uma função, crv: R → R × R. No intervalo unidade, I, nós podemos ter uma função definida para ser um de números racionais e zero caso contrário, no rato: I → 2. Usando funções para X podemos considerar uma integral definida sobre o intervalo unidade a ser uma função, int: [I → R] → R.
No entanto, ainda não estamos satisfeitos. Podemos querer ainda mais generalidade, como uma função cujo integral é uma função degrau; Assim, define assim chamada funções generalizadas. Podemos querer menos generalidade, como uma função sempre podemos realmente usar para obter uma resposta definitiva; assim, nós definimos funções recursivas primitivas e depois nos limitar àqueles que podemos provar são efetivamente computável. Ou a gente pode querer se relacionar não apenas define, mas estruturas algébricas , completo com operações; assim, nós definimos homomorphisms.
História
A história do conceito de função em matemática é descrita pela da Ponte (1992). Como um termo matemático, "função" foi cunhado por Gottfried Leibniz em 1694, para descrever uma quantidade relacionada a uma curva , como uma curva de encosta a uma específica ponto. As funções Leibniz considerados são chamados hoje funções diferenciáveis . Para este tipo de função, pode-se falar de limites e derivados ; ambos são medidas do saída ou a mudança na saída, uma vez que depende da entrada ou a mudança na entrada. Tais funções são a base de cálculo .
A função de palavra foi usada mais tarde por Leonhard Euler durante meados do século 18 para descrever um expressão ou fórmula envolvendo diversos argumentos, por exemplo, f (x) = sin (x) + x 3.
Durante o século 19, os matemáticos começaram a formalizar todos os diferentes ramos da matemática. Weierstrass defendeu a construção de cálculo em aritmética em vez de geometria , o que favoreceu a definição de Euler sobre Leibniz (ver aritmetização de análise).
No início, a idéia de uma função era bastante limitado. Joseph Fourier, por exemplo, afirmou que todas as funções teve um Série de Fourier, algo que nenhum matemático afirmaria hoje. Ao ampliar a definição de funções, os matemáticos foram capazes de estudar "estranhos" objetos matemáticos tais como funções contínuas que são em nenhuma parte diferenciável. Essas funções foram pensados primeiro a ser apenas curiosidades teóricas, e eles foram chamados coletivamente "monstros" tão tarde quanto na virada do século 20. Técnicas No entanto, a partir de poderosas análise funcional mostraram que estas funções são, em algum sentido "mais comum" de funções diferenciáveis. Tais funções já foram aplicados à modelagem de fenômenos físicos, tais como Movimento browniano.
Perto do final do século 19, os matemáticos começaram a formalizar toda a matemática usando a teoria dos conjuntos , e eles procuraram definir cada objeto matemático como um definido. Dirichlet e Lobachevsky são tradicionalmente creditado com a doação independentemente da definição "formal" moderna de uma função como uma relação em que cada primeiro elemento tem um segundo elemento único, mas a afirmação de Dirichlet para esta formalização é disputada por Imre Lakatos:
- Não existe tal definição nas obras de Dirichlet em tudo. Mas há ampla evidência de que ele não tinha idéia deste conceito. Em seu [1837], por exemplo, quando ele discute funções contínuas por partes, ele diz que em pontos de descontinuidade a função tem dois valores: ...
- (Provas e Refutações, 151, Cambridge University Press 1976)
Hardy (1908, pp. 26-28) definida como uma função de uma relação entre duas variáveis x e y tais que "para alguns valores de x, em qualquer taxa correspondem valores de y." Ele não necessária a função a ser definida para todos os valores de x, nem para associar cada valor de x para um único valor de y. Essa ampla definição de uma função engloba mais do que as relações são normalmente consideradas funções em matemática contemporânea.
A noção de uma função como uma regra para computação, em vez de um tipo especial de relação, tem sido extensivamente estudada em lógica matemática e ciência da computação teórica. Modelos para estes calculáveis funções incluem a lambda cálculo, o funções μ-recursivas e Máquinas de Turing.
Vocabulário
A entrada específica em uma função é chamado de argumento da função. Para cada valor de argumento x, y o único correspondente no codomain é chamado o valor da função em x, ou o Imagem de x sob ƒ. A imagem de x pode ser escrito como f (x) ou como Y. (Veja a seção sobre notação .)
O gráfico de uma função f é o conjunto de tudo pares ordenados (x, f (x)), para todos os x no domínio X. Se X e Y são subconjuntos de R, os números reais, em seguida, esta definição coincide com o sentido familiar de "gráfico" como uma imagem ou gráfico da função, com os pares ordenados sendo as coordenadas cartesianas de pontos.
O conceito de que a imagem pode ser estendida a partir da imagem de um ponto para a imagem de um definido. Se A é qualquer subconjunto do domínio, em seguida, f (A) é o subconjunto da gama que consiste de todas as imagens de elementos de A. dizer o ácido (A) é a imagem de uma por f.
Note-se que a gama de f é o ƒ imagem (X) do seu domínio, e que a gama de f é um subconjunto da sua codomain.
O preimage (ou imagem inversa, ou mais precisamente, imagem inversa completa) de um subconjunto B do codomain Y sob uma função f é o subconjunto do domínio definido por X
Assim, por exemplo, o preimage de {4, 9} sob a função quadrática é o conjunto {-3, -2, 2 +, + 3}.
Em geral, o pré-imagem de uma conjunto singleton (um conjunto com exatamente um elemento) pode conter qualquer número de elementos. Por exemplo, se f (x) = 7, em seguida, o preimage de {5} é o conjunto vazio, mas o preimage de {7} é a totalidade do domínio. Assim, o preimage de um elemento na codomain é um subconjunto do domínio. A convenção usual sobre o preimage de um elemento que é ƒ -1 (b) significa ƒ -1 ({b}), ou seja
Três tipos importantes de função são o injecções (funções ou one-to-one), que têm a propriedade de que se f (a) = f (b), em seguida, uma obrigação igual b; o surjections (ou para funções), que têm a propriedade de que para cada y na codomain existe um x no domínio tal que f (x) = y; e o bijeções, os quais são ambos de um-para-um e para. Esta nomenclatura foi introduzido pela Grupo Bourbaki.
Quando a primeira definição de função dada acima é usado, uma vez que o codomain não está definido, o "surjection" deve ser acompanhado de uma declaração sobre o conjunto da função mapeia para. Por exemplo, poderíamos dizer mapas ƒ para o conjunto de todos os números reais.
Restrições e extensões
Informalmente, uma restrição de uma função f é o resultado de aparar seu domínio.
Mais precisamente, se f é uma função de um X para Y, e S é qualquer subconjunto de X, a restrição de ƒ para S é a função ƒ | S de S a Y tal que ƒ | S (s) = f (s ) para todas as s em S.
Se g é qualquer restrição de ƒ, dizemos que ƒ é uma extensão do g.
Notação
É comum para omitir os parênteses em torno do argumento quando há pouca chance de ambiguidade, assim: sin x. Em alguns contextos formais, usar de notação polonesa reversa, x ƒ, elimina a necessidade de qualquer parênteses; e, por exemplo, o factorial função é sempre escrito n!, apesar de sua generalização, a função gama, é escrito Γ (n).
Descrição formal de uma função tipicamente envolve o nome da função, seu domínio, sua codomain, e uma regra de correspondência. Assim, vemos com frequência uma notação de duas partes, sendo um exemplo
onde a primeira parte é lido:
- "Ƒ é uma função de N a R" (um muitas vezes escreve informalmente "Vamos ƒ: X → Y" para significar "Vamos ƒ ser uma função de X para Y"), ou
- "Ƒ é uma função de N em R", ou
- "F é uma função R -valued de um N -valued variável",
ea segunda parte é lido:
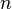 mapeia para
mapeia para 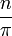
Aqui, a função chamada "ƒ" tem os números naturais como domínio, os números reais como codomain e mapas n para si dividido por π. Menos formalmente, esta forma longa pode ser abreviada
embora com alguma perda de informação; já não são explicitamente dado o domínio e contradomínio. Mesmo a forma longa aqui abrevia o facto de o n no lado da mão direita é silenciosamente tratado como um número real utilizando a incorporação padrão.
Uma alternativa para a notação do cólon, conveniente quando as funções estão a ser composta, escreve o nome da função acima da seta. Por exemplo, se ƒ é seguido por G, onde G produz o número complexo e i x, podemos escrever
Uma forma mais elaborada deste é a diagrama comutativo.
A utilização de ácido (A), para denotar a imagem de um subconjunto A ⊆ X é consistente enquanto não existir qualquer subconjunto do domínio é também um elemento do domínio. Em alguns campos (por exemplo, em conjunto teoria, onde ordinais são também define de ordinais) é conveniente ou mesmo necessário distinguir os dois conceitos; a notação usual é ƒ [A] para o conjunto {ƒ (x): x ∈ A}; alguns autores ƒ` x, em vez de f (x), e ƒ`` A em vez de ƒ [A].
Composição de função
A composição de função de duas ou mais funções usa a saída de uma função de como a entrada de outro. Por exemplo, f (x) = sin (x 2) é a composição da função seno e a função quadrática. As funções ƒ: X → Y e g: Y → Z pode ser composta por primeiro aplicar ƒ para um argumento x para obter y = f (x) e, em seguida, aplicando g de y para obter Z = G (y). A função composta formada deste modo a partir geral ƒ g e pode ser escrita
A função à direita age primeiro e a função do lado esquerdo age segundo, invertendo a ordem de leitura Inglês. Lembramo-nos a ordem através da leitura da notação como "g de ƒ". A ordem é importante, porque raramente é que vamos obter o mesmo resultado em ambos os sentidos. Por exemplo, suponha que f (x) = x 2 e g (x) = x 1. Em seguida, g (ƒ (x)) x 2 = 1, enquanto que f (g (x)) = (x + 1) 2, que é 2 x 2 x 1, uma função diferente.
Função identidade
A única função sobre um conjunto X que mapeia cada elemento em si é chamado para a função de identidade para X e, normalmente indicada por id X. Cada conjunto tem a sua própria função de identidade, de modo que o índice não pode ser omitida, a menos que o conjunto pode ser inferida a partir do contexto. Sob composição, uma função de identidade é "neutro": se f é uma função de X para Y, em seguida,
Função inversa
Se f é uma função de X para Y, em seguida, uma função inversa de ƒ, denotada por ƒ -1, é uma função no sentido oposto, de Y para X, com a propriedade de que uma ida e volta (a composição ) retorna para cada elemento si. Não cada função tem uma inversa; aqueles que o fazem são chamados invertida.
Como exemplo simples, se converte ƒ uma temperatura em graus Celsius em graus Fahrenheit, convertendo a função graus Fahrenheit para graus Celsius seria uma -1 ƒ adequado.
A notação para composição nos lembra de multiplicação; na verdade, às vezes nós denotar-lo usando justaposição, g ƒ, sem um círculo de intervir. Sob essa analogia, as funções de identidade são como um, e funções inversas são como recíprocos (daí a notação).
Especificar uma função
Uma função pode ser definida por qualquer condição matemática relacionando cada argumento para o valor de saída correspondente. Se o domínio é finito, uma função f pode ser simplesmente definida por tabulação de todos os argumentos x e os seus correspondentes valores de função ƒ (x). Mais comumente, uma função é definida por uma fórmula , ou (mais geralmente) um algoritmo - uma receita que explica como calcular o valor de f (x) qualquer dado x no domínio.
Há muitas outras maneiras de definição de funções. Exemplos incluem recursão, ou algébrica analítico encerramento, limites , continuação analítica, infinito série, e como soluções de integrais e equações diferenciais . O lambda cálculo fornece uma poderosa e flexível sintaxe para definir e combinar funções de várias variáveis.
Computability
Funções que enviam inteiros para inteiros, ou seqüências finitas para finita cordas, às vezes pode ser definido por um algoritmo , o que dá uma descrição precisa de um conjunto de passos para calcular a saída da função de sua entrada. Funções definíveis por um algoritmo são chamados funções computáveis. Por exemplo, a Algoritmo de Euclides dá um processo preciso para calcular o máximo divisor comum de dois números inteiros positivos. Muitas das funções estudadas no contexto da teoria dos números são computáveis.
Resultados fundamentais da teoria da computabilidade mostram que há funções que podem ser definidos com precisão, mas não são computáveis. Além disso, no sentido de cardinalidade, quase todas as funções de inteiros para inteiros não são computáveis. O número de funções computáveis a partir de números inteiros para inteiros é contável, porque o número de possíveis algoritmos é. O número de todas as funções de inteiros para inteiros é mais elevada: o mesmo que a cardinalidade dos números reais . Assim, a maioria das funções de inteiros para inteiros não são computáveis. Exemplos específicos de funções incalculável são conhecidos, incluindo o função do castor ocupado e funções relacionadas com o problema da parada e outras problemas indecidíveis.
Funções com múltiplas entradas e saídas
O conceito de função pode ser alargada a um objecto que tem uma combinação de duas (ou mais) valores de argumento para um único resultado. Este conceito intuitivo é formalizada por uma função cujo domínio é o Produto cartesiano de dois ou mais conjuntos.
Por exemplo, considere a multiplicação função que associa dois números inteiros para os seus produtos: f (x, y) = x · y. Esta função pode ser definida formalmente como tendo domínio Z × Z, o conjunto de todos os pares de números inteiros; codomain Z; e, para o gráfico, o conjunto de todos os pares ((x, y), x · y). Note-se que o primeiro componente de um tal par é em si um par (de inteiros), enquanto que o segundo componente é um único número inteiro.
O valor da função do par (x, y) é ácido ((x, y)). No entanto, é habitual retirar um conjunto de parênteses e considerar f (x, y) em função de duas variáveis (ou com dois argumentos), x e y.
O conceito pode ser estendido ainda mais, considerando uma função que também produz uma saída que é expresso como diversas variáveis. Por exemplo, considere a função de espelho (x, y) = (y, x) com o domínio R × R e R x R codomain bem. O par (y, x) é um valor único na codomain visto como um produto cartesiano.
Operações binárias
O familiar operações binárias de aritmética , adição e multiplicação , pode ser visto como funções de R x R a R. Esta opinião é generalizada em álgebra abstrata , onde as funções n -ary são usados para modelar as operações de estruturas algébricas arbitrárias. Por exemplo, um resumo grupo é definido como um conjunto X e uma função f de X × X para X que satisfaz certas propriedades.
Tradicionalmente, adição e multiplicação estão escritos no notação infixa: x + y e x x y em vez de + (x, y) e x (x, y).
Espaços funcionais
O conjunto de todas as funções de um conjunto X para um conjunto Y é denotado por X → Y, pela [X → Y], ou por Y X. Esta última notação é justificada pelo fato de que | Y X | = | Y | | X | e é um exemplo de a convenção de combinatória enumerativa que fornece notações para conjuntos com base em suas cardinalities.
Veja o artigo sobre números cardinais para mais detalhes.
Podemos interpretar ƒ: X → Y significa ƒ ∈ [X → Y]; isto é, "ƒ é uma função de X para Y".
Operações pontuais
Se ƒ: X → R e g: X → R são funções com domínio comum X e um comum codomain anel R, então pode-se definir a função soma ƒ + g: X → R ea função do produto ƒ ⋅ g: X → R como segue:
para todo x em X.
Isso transforma o conjunto de todas as funções em um anel. As operações binárias em que o anel tem como domínio pares ordenados de funções, e como funções codomain. Este é um exemplo de subir na abstração, para funções de tipos mais complexos.
Ao tomar alguma outra estrutura algébrica A no lugar de R, pode-se transformar o conjunto de todas as funções de X para A em uma estrutura algébrica do mesmo tipo de uma forma análoga.
Outras propriedades
Há muitas outras classes especiais de funções que são importantes para determinados ramos da matemática, ou aplicações específicas. Aqui está uma lista parcial:
- bijection, injeção e surjection. Você também pode visitar função injetora, função e surjective função bijective separadamente.
- contínuo
- diferenciável, integrável
- linear, polinomial , racional
- algébrica, transcendental
- trigonométrico
- fractal
- par ou ímpar
- convexo, monótona, unimodal
- holomorphic, meromorfa, todo
- vectorial
- computável