Renormalization

Assuntos Relacionados: Física

Informações de fundo

Esta seleção Wikipedia está offline disponível a partir de Crianças SOS, para distribuição no mundo em desenvolvimento. patrocínio SOS Criança é legal!

Teoria quântica de campos
Feynman diagrama
História
Fundo Teoria de campo Teoria de gauge Poincaré simetria Mecânica quântica Quebra espontânea de simetria
Simetrias Carga conjugação Cruzamento Paridade Reversão do tempo
Ferramentas Anomalia Teoria de campo efetivo Valor esperado Fantasmas Faddeev-Popov Feynman diagrama Teoria do retículo de gauge Fórmula de redução LSZ Função de partição Propagator Quantização Regularização Renormalization Estado de vácuo Teorema de Wick Axiomas Wightman
Equações Equação de Dirac Equação de Klein-Gordon Equações Proca Equação Wheeler-DeWitt Equações Bargmann-Wigner
Modelo Padrão Interação eletrofraca Mecanismo de Higgs Cromodinâmica quântica Eletrodinâmica quântica Teoria de Yang-Mills
Teorias incompletas A gravidade quântica A teoria das cordas Supersimetria Technicolor Teoria de tudo
Os cientistas CD Anderson PW Anderson Bardeen Bethe Bjorken Bogoliubov Brout Cabibbo Callan Cronin DeWitt Dirac Dyson Englert Fermi Feynman Fierz Pescador Fock Fröhlich Gell-Mann Bruto Hänsch Heisenberg Higgs Haag 'T Hooft Kadanoff Kendall Klitzing Kobayashi Cordeiro Landó Sotavento Majorana Maskawa Mills Nambu Nishijima Parisi Paul Polyakov Salam Schwinger Shockley Skyrme Störmer Sudarshan Thomson Tomonaga Veltman Enfermaria Weinberg Wilczek Wilson Yang Yukawa

Em teoria quântica de campo , as mecânica estatística de campos, ea teoria da estruturas geométricas auto-similares, renormalization refere-se a um conjunto de técnicas utilizadas para tomar um limite do contínuo.

Ao descrever o espaço eo tempo como um continuum, certas construções mecânicas e estatísticos quânticos estão mal definidos. De modo a defini-los, o limite contínuo tem que ser feita com cuidado.

Renormalização determina a relação entre os parâmetros na teoria, quando os parâmetros que descrevem escalas grandes distâncias diferentes dos parâmetros que descrevem a pequenas distâncias. Renormalization foi desenvolvido pela primeira vez em eletrodinâmica quântica (QED) para dar sentido a infinitas integrais em teoria de perturbação. Inicialmente visto como um suspeito, procedimento provisório por alguns dos seus criadores, renormalization eventualmente foi abraçado como um importante e ferramenta de auto-consistente em vários campos da física e matemática .

As auto-interações na física clássica

Figura 1. Renormalization em eletrodinâmica quântica: A interação elétron-fóton simples que determina carga do elétron em um ponto renormalization é revelada a consistem de interações mais complicadas na outra.

O problema dos infinitos surgiu pela primeira vez no eletrodinâmica clássica de partículas pontuais no século 19 e início do século 20.

A massa de uma partícula carregada deve incluir o consumo de energia em massa no seu campo electrostático. Assume-se que a partícula é uma concha esférica carregada de raio $r_e$ . A energia no campo está

$m_ \ mathrm {em} = \ int \ operatorname {d} V {1 \ over 2} E ^ 2 = \ int_ {r_e} ^ \ infty dr 4 \ pi r ^ 2 \ left ({q \ over 4 \ pi r ^ 2} \ right) ^ 2 = {q ^ 2 \ over 4 \ pi r_e}$

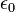e é infinito quando $r_e$ é zero. O valor de $r_e$ que faz $m _ {\ mathrm {em}}$ igual à massa de electrões é denominado raio de elétrons clássica. Com fatores de c e $\ Epsilon_0$ restaurado:

$r_e = {q ^ 2 \ over 4 \ pi \ epsilon_0 m_e c ^ 2} \ approx {1 \ over 137} {\ hbar \ over m_e c} \ approx 2,8 \ times 10 ^ {- 15} \, \ mathrm { m}.$

É assim $\ Alpha$ vezes menor do que o Compton comprimento de onda do elétron.

A massa de uma partícula esférica carregada inclui a massa do reservatório esférico. Se a massa do escudo é permitida a ser negativo, pode ser possível ter um limite ponto consistente. Isto foi chamado renormalização, e Lorentz e Abraham tentou desenvolver uma teoria clássica do elétron desta forma. Este trabalho inicial foi a inspiração para posteriores tentativas de regularização e renormalização na teoria quântica de campos.

Ao calcular os eletromagnéticas interações dos praticados partículas, é tentador ignorar o back-reacção de campo próprio de uma partícula em si. Mas essa reação de volta é necessária para explicar o atrito com partículas carregadas quando eles emitem radiação. Se o electrão é assumido como sendo um ponto, o valor da parte de trás-reacção diverge, pela mesma razão que a massa diverge, porque o campo está inverso do quadrado.

O Teoria Abraham-Lorentz tinha um não-causal "pré-aceleração". Às vezes, um elétron iria começar a se mover antes de a força é aplicada. Este é um sinal de que o limite de pontos é inconsistente. Um corpo estendido começará a se mover quando uma força é aplicada dentro de um raio do centro de massa.

O problema era pior em teoria clássica dos campos do que em teoria quântica de campos, porque em teoria quântica de campos uma partícula carregada em distâncias curtas podem flutuar em uma antipartícula. A antipartícula tem carga oposta, e as flutuações manchar a carga ao longo de uma região comparável ao comprimento de onda Compton. Em electrodinâmica quântica na pequena da massa de acoplamento electromagnética única diverge como o log do raio da partícula.

Muitos físicos acreditam que, quando a constante de estrutura fina é muito maior do que um, de modo que o raio de elétrons clássica é maior do que o comprimento de onda quântica, os mesmos problemas que afligem a eletrodinâmica clássica ainda estão presentes na eletrodinâmica quântica.

Divergências na eletrodinâmica quântica

Figura 2. Um diagrama contribuindo para elétron-elétron dispersão em QED. O circuito tem uma divergência ultravioleta.

Vacuum polarização, aka cobrar triagem. Este laço tem uma divergência ultravioleta logarítmica.

Auto diagrama de energia em QED.

Ao desenvolver eletrodinâmica quântica na década de 1930, Max Born, Werner Heisenberg, Pascual Jordan, e Paul Dirac descobriu que em cálculos perturbativos muitas integrais foram divergentes.

Uma maneira de descrever as divergências foi descoberto na década de 1930 por Ernst Stueckelberg, na década de 1940 por Julian Schwinger, Richard Feynman , e Shin'ichiro Tomonaga, e sistematizado por Freeman Dyson. As divergências aparecem em cálculos que envolvem Diagramas de Feynman com circuitos fechados de partículas virtuais neles.

Enquanto as partículas virtuais obedecer conservação de energia e impulso , eles podem ter qualquer energia e momento, mesmo que não é permitido pela relação energia-momentum relativista para a massa observada de que partículas. (Isto é, $E ^ 2-p ^ 2$ não é necessariamente a massa da partícula em que o processo (por exemplo, para um fotão pode ser diferente de zero).) Uma tal partícula é chamada off-shell. Quando há um loop, a dinâmica das partículas envolvidas no circuito não é determinado unicamente pelas energias e momentos de partículas de entrada e saída. Uma variação na energia de uma partícula no circuito pode ser contrabalançado por uma variação igual e oposto na outra partícula de energia no circuito. Então, para encontrar a amplitude do processo em malha deve integrar sobre todas as combinações possíveis de energia e momento que poderia viajar ao redor do loop.

Estas integrais são muitas vezes divergentes, isto é, eles dão respostas infinitas. As divergências que são significativos são o " ultravioletas "(UV) queridos. Uma divergência ultravioleta pode ser descrita como uma que vem

- A região na integral onde todas as partículas no circuito têm grandes energias e impulso.

- Muito curto comprimentos de onda e alta frequências flutuações dos campos, no caminho integral para o campo.

- Em tempo adequado Muito curto entre a emissão de partículas e absorção, se o loop é pensado como uma soma sobre caminhos de partículas.

Então, essas divergências são de curta distância, fenômenos de curta duração.

Há exatamente três diagramas de loops divergente de um loop na eletrodinâmica quântica.

um fóton cria um elétron virtual par de positrões, que, em seguida, aniquilar, este é um diagrama de polarização vácuo.
um elétron que rapidamente emite e reabsorve um fóton virtual, chamado de uma auto-energia.
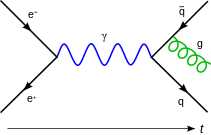
Um elétron emite um fóton, emite-se um segundo fóton, e reabsorve o primeiro. Este processo é mostrado na figura 2, e é chamado um vértice de renormalização.

Os três divergências correspondem aos três parâmetros na teoria:

a Z. campo normalização
a massa do electrão.
a carga do elétron.

Uma segunda classe de divergência, um chamado divergência de infravermelhos, é devido a partículas sem massa, como o fóton. Todo processo envolvendo partículas carregadas emite infinitamente muitos fótons coerentes de comprimento de onda infinita, ea amplitude para emitir qualquer número finito de fótons é zero. Para fótons, essas divergências são bem compreendidos e não são uma fonte de controvérsia.

A divergência de loop

O diagrama na Figura 2 mostra uma das diversas contribuições de um loop para elétron-elétron dispersão em QED. O electrões no lado esquerdo do diagrama, representada pela linha a cheio, começa com quatro impulso $p ^ \ mu$ e termina com quatro impulso $r ^ \ mu$ . Ele emite um fóton virtual de transporte $r ^ \ mu - p ^ \ mu$ para transferir a energia e quantidade de movimento para o outro de electrões. Mas neste diagrama, antes que isso aconteça, ele emite outro fóton virtual transportando quatro-momentum $q ^ \ mu$ , E que reabsorve este um após o outro emissor de fotões virtual. Energia e conservação do momento não determinam o quatro-momentum $q ^ \ mu$ com exclusividade, por isso todas as possibilidades contribuir de forma igual e que deve integrar.

Esta amplitude do diagrama acaba com, entre outras coisas, um factor do circuito de

$ie ^ 3 \ int {d ^ 4 q \ over (2 \ pi) ^ 4} \ gamma ^ \ mu {i (\ gamma ^ \ alpha (rq) _ \ alpha + m) \ over (rq) ^ 2 - m ^ 2 + i \ epsilon} \ gamma ^ \ rho {i (\ gamma ^ \ beta (pq) _ \ beta + m) \ over (pq) ^ 2 - m ^ 2 + i \ epsilon} \ gamma ^ \ nu {g -i _ {\ mu \ nu} \ mais q ^ 2 + i \ epsilon}$

As várias $\ Gamma ^ \ mu$ fatores nessa expressão são matrizes gama como na formulação do covariante Equação de Dirac; eles têm a ver com o spin do elétron. Os factores de $e$ são a constante de acoplamento eléctrico, enquanto o $i \ epsilon$ proporcionar uma definição heurística do contorno de integração em torno dos pólos no espaço de momentos. A parte importante para os nossos propósitos é a dependência de $q ^ \ mu$ dos três grandes fatores do integrando, que são do propagadores das duas linhas de elétrons e fótons da linha no loop.

Isto tem um pedaço com dois poderes de $q ^ \ mu$ no topo que domina em grandes valores de $q ^ \ mu$ (Pokorski 1987, p 122).:

$e ^ 3 \ gamma ^ \ mu \ gamma ^ \ alpha \ gamma ^ \ rho \ gamma ^ \ beta \ gamma_ \ mu \ int {d ^ 4 q \ over (2 \ pi) ^ 4} {q_ \ alpha q_ \ beta \ over (rq) ^ 2 (pq) ^ 2 q ^ 2}$

Esta integral é divergente, e infinito, a menos que cortá-lo em energia finita e momento de alguma forma.

Divergências de loop semelhantes ocorrem em outras teorias quânticas de campo.

Renormalizada e quantidades nuas

A solução foi perceber que as quantidades inicialmente que aparecem nas fórmulas da teoria (por exemplo, a fórmula para o Lagrangeanos), representando tais coisas como o electrão de carga eléctrica e em massa , assim como a normalização do quantum campos-se, na verdade, não correspondem às constantes físicas medidos em laboratório. Como escrito, eram quantidades nuas que não levam em conta a contribuição de efeitos de loop de partículas virtuais para os próprios constantes físicas. Entre outras coisas, esses efeitos que incluem a contrapartida quântica do back-reação eletromagnética que então afligiam teóricos clássicos do eletromagnetismo. Em geral, estes efeitos seria tão divergentes quanto as amplitudes em estudo em primeiro lugar; grandezas medidas tão finitos que em geral implica quantidades descalços divergentes.

A fim de fazer contato com a realidade, então, as fórmulas teria de ser reescrita em termos de quantidades mensuráveis, renormalizada. A carga do electrão, por exemplo, pode ser definido em termos de uma quantidade específica medida a uma cinemática renormalização ponto ou ponto de subtracção (que geralmente têm uma energia característica, chamada de escala ou simplesmente a renormalização escala de energia). As partes do Lagrangian sobra, envolvendo as porções remanescentes das quantidades nuas, poderia então ser reinterpretado como counterterms, envolvido em diagramas divergentes exatamente anulando as divergências incômodos para outros diagramas.

Renormalization em QED

Figura 3. O vértice correspondente ao Z ₁ counterterm cancela a divergência na Figura 2.

Por exemplo, no Lagrangian de QED

$\ Mathcal {L} = \ bar \ psi_B \ left [i \ gamma_ \ mu (\ partial ^ \ mu + ie_BA_B ^ \ mu) -m_B \ right] \ psi_B - \ frac {1} {4} F_ {B \ mu \ nu} F_B ^ {\ mu \ nu}$

os campos e constante de acoplamento são quantidades realmente nuas, daí o subscrito 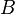$B$ acima. Convencionalmente as quantidades nuas são escritas de modo que os termos de Lagrange correspondentes são múltiplos de os renormalizada:

$\ Left (\ bar \ psi m \ psi \ right) = _B z_0 \, \ bar \ psi m \ psi$

$\ Left (\ bar \ psi (\ partial ^ \ mu + iea ^ \ mu) \ psi \ right) = _B Z_1 \, \ bar \ psi (\ partial ^ \ mu + iea ^ \ mu) \ psi$

$\ left (F _ {\ mu \ nu} F ^ {\ mu \ nu} \ right) = _B Z_3 \, F _ {\ mu \ nu} F ^ {\ mu \ nu}$ .

( Medida invariância, através de um Identidade Ward-Takahashi, acaba por implicar que podemos renormalizar os dois termos da peça derivada covariante $\ Bar \ psi (\ partial + AIE) \ psi$ juntos (Pokorski 1987, p. 115), que é o que aconteceu com $Z_2$ ; é o mesmo que $Z_1$ .)

Um termo neste Lagrangeanos, por exemplo, a interacção de electrões-fótons representado na Figura 1, pode então ser escrito

$\ Mathcal {L} = -e _I \ bar \ psi \ gamma_ \ mu A ^ \ mu \ psi \, - \, (Z_1 - 1) e \ bar \ psi \ gamma_ \ mu A ^ \ mu \ psi$

A constante física $e$ , Carga do elétron, pode, então, ser definida em termos de alguma experiência específica; vamos definir a escala renormalization igual à energia característica deste experimento, eo primeiro termo dá a interação vemos no laboratório (até pequenas correções finitos a partir de diagramas de loops, proporcionando exóticas como as correções de alta ordem para a momento magnético). O resto é a counterterm. Se tivermos sorte, as partes divergentes de diagramas de loops podem ser decomposto em peças com três ou menos pernas, com uma forma algébrica que pode ser cancelado pelo segundo mandato (ou pelos counterterms semelhantes que vêm de $Z_0$ e $Z_3$ ). Em QED, temos a sorte: a teoria é renormalizável (veja abaixo mais informações sobre isso).

O diagrama com o $Z_1$ interacção do vértice counterterm colocada como na figura 3 anula a divergência a partir do circuito na Figura 2.

A divisão dos "termos nus" para os termos e counterterms originais veio antes do percepções de grupo de renormalização devido a Kenneth Wilson. De acordo com renormalization idéias do grupo, esta divisão não é natural e não físico.

Correr constantes

Para minimizar a contribuição de diagramas de loops de um determinado cálculo (e, portanto, torná-lo mais fácil de extrair resultados), um escolhe um ponto renormalization perto das energias e momentos realmente trocadas na interação. No entanto, o ponto de renormalização não é por si só uma quantidade física: as previsões físicas da teoria, calculados para todos os pedidos, deve em princípio ser independente da escolha do ponto de renormalização, desde que esteja dentro do domínio de aplicação da teoria. Mudanças na escala renormalization simplesmente vai afetar quanto de um resultado vem de diagramas de Feynman sem loops, e quanto vem das partes de sobra finitos de diagramas de loops. Pode-se explorar esse fato para calcular a variação efetiva de constantes físicas com mudanças de escala. Esta variação é codificado pela -funções beta, e a teoria geral deste tipo de escala-dependência é conhecida como a grupo de renormalização.

Coloquialmente, os físicos de partículas, muitas vezes falar de certas constantes físicas como variando com a energia de uma interação, embora, de fato, é a escala renormalization que é a quantidade independente. Este running, no entanto, fornecer um meio conveniente de descrever mudanças no comportamento de uma teoria de campo sob mudanças nas energias envolvidas em uma interação. Por exemplo, uma vez que a constante de acoplamento em cromodinâmica quântica torna-se pequeno em escalas de energia de grande porte, a teoria se comporta mais como uma teoria livre como a energia trocada em uma interação se torna grande, um fenômeno conhecido como liberdade assintótica. Escolhendo uma escala crescente de energia e usando o grupo de renormalização deixa isso claro a partir de diagramas de Feynman simples; foram este não for feito, a previsão seria o mesmo, mas iriam surgir de cancelamentos de alta ordem complicadas.

Regularização

Uma vez que a quantidade $\ Infty - \ infty$ está mal definido, a fim de tornar essa noção de cancelamento divergências precisos, as divergências primeiro tem que ser domado matematicamente usando a teoria de limites , em um processo conhecido como regularização.

Uma modificação essencialmente arbitrária para os integrandos de loop, ou regulador, pode fazê-los cair mais rapidamente em altas energias e momentos, de tal maneira que as integrais convergem. Um regulador tem uma escala de energia característica conhecida como a cortar; tomar este corte para o infinito (ou, de forma equivalente, a escala de comprimento / hora correspondente a zero) recupera as integrais originais.

Com o regulador no local, e um valor finito para a corte, os termos divergentes nos integrais, em seguida, transformar-se em termos finitos, mas dependente de corte. Depois de cancelar estes termos com as contribuições de counterterms dependente de corte, o corte é levado ao infinito e resultados físicos finitos recuperado. Se a física em escalas que podemos medir é independente do que acontece com os muito mais curtas escalas de distância e de tempo, então deve ser possível obter resultados independente de corte para cálculos.

Muitos tipos diferentes de reguladores são utilizados nos cálculos da teoria quântica campo, cada um com as suas vantagens e desvantagens. Um dos mais populares no uso moderno é regularização dimensional, inventado por Gerardus 't Hooft e Martinus JG Veltman, que doma as integrais por carregá-los em um espaço com um número fracionário fictícia de dimensões. Outra é Regularização Pauli-Villars, que adiciona partículas fictícias com a teoria com muito grandes massas, de modo que integrandos de loop envolvendo as partículas massivas anular os laços existentes em geral momentos.

Ainda um outro esquema de regularização é o Regularização estrutura, introduzida pelo Kenneth Wilson, que finge que nosso espaço-tempo é construído pela estrutura hiper-cúbica com tamanho fixo grid. Este tamanho é um corte natural para o impulso máximo que uma partícula pode possuir, quando de propagação sobre a estrutura. E depois de fazer o cálculo em várias treliças com diferentes tamanhos grid, o resultado físico é extrapolados para grade de tamanho 0, ou o nosso universo natural. Isto pressupõe a existência de um escamação limite.

Uma abordagem matemática rigorosa à teoria de renormalização é o chamado teoria de perturbação causal, onde as divergências ultravioletas são evitadas desde o início nos cálculos através da realização de operações matemáticas bem definidas unicamente no âmbito de teoria da distribuição. A desvantagem do método é o facto de que a aproximação é completamente técnica e requer um elevado nível de conhecimento matemático.

Função Zeta regularização

Julian Schwinger descobriu uma relação entre regularização zeta função e renormalization, usando a relação assintótica:

$I (n, \ Lambda) = \ int_ {0} ^ {\ Lambda} dp \, p ^ {n} \ sim 1 + 2 + 3 ^ n ^ n + ... + \ Lambda ^ n = \ zeta (- n)$

como o regulador $\ Lambda \ rightarrow \ infty$ . Com base nisso, ele considerado usando os valores de $\ Zeta (-n)$ para obter resultados finitos. Apesar de ter alcançado resultados inconsistentes, uma fórmula melhorada por Hartle, J. Garcia, E. Elizalde inclui

$I (n, \ Lambda) = \ frac {n} {2} I (n-1, \ Lambda) + \ zeta (-n) - \ sum_ {r = 1} ^ {\ infty} \ frac {{B_ 2r}} {(2R)! a_} {n, r} (n-2r + 1), (n-2r, \ lambda)$ ,

em que s a B 'são o Números de Bernoulli e

$a_ {n, R} = \ frac {\ Gamma (n + 1)} {\ Gamma (n-2r + 2)}$ .

Assim, cada $I (m, \ Lambda)$ pode ser escrita como uma combinação linear de $\ Zeta (-1), \ zeta (-3), \ zeta (-5), ...... \ zeta (-m)$

Ou simplesmente usando Fórmula Abel-Plana temos para cada integrante divergente:

$\ Zeta (-m, \ beta) - \ frac {\ beta ^ {m}} {2} -i \ int_ 0 ^ {\ infty} dt \ frac {(it + \ beta) ^ {m} - (--lo + \ beta) ^ {m}} {e ^ {2 \ pi t} -1} = \ int_0 ^ {\ infty} dp (p + \ beta) ^ {m}$ válida quando m> 0, Aqui a função Zeta é Função zeta de Hurwitz e Beta é um número real positivo.

A analogia "geométrico" é dada por, (se usarmos método retângulo) para avaliar a integral da seguinte forma:

$\ Int_ {0} ^ {\ infty} dx (\ beta + x) ^ {m} \ approx \ sum_ {n = 0} ^ {\ infty} {h ^ m + 1} \ zeta (\ beta h ^ { -1}, -m)$

Usando Hurwitz regularização zeta mais método retângulo com o passo h (para não ser confundido com Constante de Planck)

Atitudes e interpretação

Os primeiros formuladores de QED e outras teorias quânticas de campo eram, em regra, insatisfeito com este estado de coisas. Parecia ilegítimo fazer algo equivalente a subtrair infinidades de infinidades de obter respostas finitas.

Dirac crítica 's foi o mais persistente. Tão tarde quanto 1975, ele estava dizendo:

A maioria dos físicos estão muito satisfeitos com a situação. Eles dizem: 'A eletrodinâmica quântica é uma boa teoria e não temos que se preocupar com mais nada. " Devo dizer que estou muito satisfeito com a situação, porque esta chamada "boa teoria" implica descuidar infinidades que aparecem em suas equações, negligenciá-los de forma arbitrária. Este não é apenas matemática sensatas. Matemática sensatas envolve negligenciar uma quantidade quando é pequena - não negligenciá-lo só porque é infinitamente grande e você não quer!

Outro crítico importante foi Feynman . Apesar de seu papel crucial no desenvolvimento da eletrodinâmica quântica, ele escreveu o seguinte em 1985:

O jogo shell que nós jogamos ... é tecnicamente chamado de "renormalização". Mas não importa o quão inteligente a palavra, ainda é o que eu chamaria um processo dippy! Ter de recorrer a tais abracadabra nos impediu de provar que a teoria da eletrodinâmica quântica é matematicamente auto-consistente. É surpreendente que a teoria ainda não foi comprovada auto-consistente uma forma ou de outra por agora; Eu suspeito que renormalization não é matematicamente legítimo.

Enquanto a crítica de Dirac foi baseado no procedimento de renormalização em si, a crítica de Feynman foi muito diferente. Feynman estava preocupado que todas as teorias de campo conhecidos na década de 1960 tinha a propriedade de que as interações se torna infinitamente forte em escalas de distância curta o suficiente. Esta propriedade, chamada de Landau pólo, tornou plausível que as teorias quânticas de campo foram todos inconsistente. Em 1974, Gross, Politzer e Wilczek mostrou que uma outra teoria quântica de campos, Cromodinâmica Quântica, não tem um pólo landau. Feynman, juntamente com a maioria dos outros, aceitou que QCD era uma teoria totalmente consistente.

O mal-estar geral era quase universal em textos até os anos 1970 e 1980. A partir de 1970, no entanto, inspirado pelo trabalho no grupo de renormalização e teoria de campo efetivo, e apesar do fato de que Dirac e vários outros - todos eles pertenciam à geração mais velha - não retirou suas críticas, as atitudes começaram a mudar, especialmente entre os teóricos mais jovens. Kenneth G. Wilson e outros demonstraram que o grupo de renormalização é útil em estatística aplicada a teoria de campo da física da matéria condensada , onde ele fornece importantes insights sobre o comportamento dos transições de fase. Em física da matéria condensada, existe um regulador real de curto distância: a matéria deixa de ser contínua na escala de átomos . Divergências curta distância em física da matéria condensada não apresentam um problema filosófico, uma vez que a teoria de campo é apenas uma representação efetiva, alisou-out do comportamento da matéria de qualquer maneira; não existem infinidades uma vez que o corte é, na verdade, sempre finito, e faz todo o sentido que as quantidades nuas são dependentes da corte.

Se QFT detém toda a maneira para baixo após o Comprimento de Planck (onde ele pode ceder a teoria das cordas , causal teoria dos conjuntos ou algo diferente), então não pode haver nenhum problema real com divergências de curta distância em física de partículas , quer, todas as teorias de campo pode ser simplesmente teorias de campo efetivas. Em certo sentido, esta abordagem reflecte a atitude mais velho que as divergências em QFT falar da ignorância humana sobre o funcionamento da natureza, mas também reconhece que essa ignorância pode ser quantificada e que as teorias eficazes resultantes permanecem útil.

Em QFT, o valor de uma constante física, em geral, depende da escala que se escolhe como o ponto de renormalização, e torna-se muito interessante para examinar o funcionamento do grupo de renormalização constantes físicas sob as mudanças na escala de energia. As constantes de acoplamento no Modelo Padrão da física de partículas variam de formas diferentes com o aumento da escala de energia: o acoplamento de cromodinâmica quântica eo fraco acoplamento isospin do força eletrofraca tendem a diminuir, eo fraco acoplamento hipercarga da força eletrofraca tende a aumentar. Na escala colossal de energia de 10 ¹⁵ GeV (muito além do alcance de nossa civilização aceleradores de partículas), todos eles se tornam aproximadamente o mesmo tamanho (Grotz e Klapdor 1990, 254 p.), a principal motivação para especulações sobre grande teoria unificada. Em vez de ser apenas um problema preocupante, renormalization tornou-se uma importante ferramenta teórica para estudar o comportamento de teorias de campo em diferentes regimes.

Se uma teoria que caracteriza renormalization (por exemplo QED) só pode ser sensatamente interpretado como uma teoria de campo efetiva, ou seja, como uma aproximação que reflete a ignorância humana sobre o funcionamento da natureza, então o problema continua a ser de descobrir uma teoria mais precisa que não tem esses problemas renormalização . Como Lewis Ryder colocou, "na teoria quântica, essas divergências [clássica] não desaparecem;. Ao contrário, eles parecem piorar e apesar do sucesso comparativa da teoria renormalisation a sensação é que deve haver um mais forma satisfatória de fazer as coisas. "

Renormalizabilidade

A partir desta reavaliação filosófica um novo conceito segue naturalmente: a noção de renormalizabilidade . Nem todas as teorias prestam-se para renormalização, da maneira descrita acima, com uma fonte finita de counterterms e todas as quantidades tornando-se independente de corte no final do cálculo. Se o Lagrangian contém combinações de operadores de campo de excessivamente elevada dimensão em unidades de energia, os counterterms necessários para cancelar todas as divergências proliferam para número infinito, e, à primeira vista, a teoria parece ter um número infinito de parâmetros livres e, portanto, perder todo o poder preditivo, tornando-se cientificamente inútil. Tais teorias são chamados renormalizável.

O Modelo Padrão da física de partículas contém apenas os operadores renormalizáveis, mas as interações entre a relatividade geral se tornar operadores renormalizável se tenta construir uma teoria de campo gravidade quântica da forma mais simples, o que sugere que teoria de perturbação é inútil em aplicação a gravidade quântica.

No entanto, em uma teoria de campo efetivo ", renormalizabilidade" é, estritamente falando, um equívoco. Em uma teoria de campo efetivo renormalizável, termos no Lagrangian se multiplicam ao infinito, mas têm coeficientes reprimidas pelas potências inversas cada vez mais extremas de o corte de energia. Se o corte é uma real, a quantidade-se física, isto é, a teoria é apenas uma descrição eficaz da física até um pouco de energia máximo ou distância mínima escala então estes termos extras poderiam representar interações físicas reais. Partindo do princípio de que as constantes adimensionais na teoria não conseguir, cálculos de grupo muito grande pode-se por potências inversas do cutoff, e extrair previsões aproximados a ordem finita no cutoff que ainda tem um número finito de parâmetros livres. Ele pode até mesmo ser útil para renormalizar essas interações "renormalizável".

Interações renormalizável em teorias de campo efetivas rapidamente tornar-se mais fraca como a escala de energia torna-se muito menor do que o ponto de corte. O exemplo clássico é o Teoria de Fermi do força nuclear fraca, uma teoria renormalizável eficaz cujo corte é comparável com a massa do W partícula. Este fato também pode fornecer uma possível explicação para por que quase todas as interações de partículas que vemos são descritível por teorias renormalizáveis. Pode ser que quaisquer outros que possam existir no GUT ou escala de Planck simplesmente tornar-se demasiado fraco para detectar no reino podemos observar, com uma exceção: a gravidade , cuja interação extremamente fraco é ampliada pela presença de enormes massas de estrelas e planetas .

Esquemas de renormalização

Em cálculos reais, os counterterms introduzido para cancelar as divergências nos cálculos diagrama de Feynman além do nível de árvore deve ser fixado usando um conjunto de condições de renormalização. Os esquemas de renormalização comuns em uso incluem:

Subtração Minimal (MS) eo esquema de subtração mínima modificado relacionadas (MS-bar) esquema
On-shell esquema

Aplicação em Física Estatística

Como mencionado na introdução, os métodos de renormalização ter sido aplicado à Física estatística, a saber, os problemas do comportamento crítico perto de transições de fase de segunda ordem, em especial, a dimensões espaciais fictícios logo abaixo do número de 4, em que o acima mencionado métodos poderia mesmo ser afiada (ou seja, em vez de "renormalizabilidade" obtém-se "super-renormalizabilidade"), o que permitiu a extrapolação para a dimensionalidade espacial real para transições de fase, 3. Detalhes podem ser encontrados no livro de Zinn-Justin, mencionado abaixo .

Para a descoberta destas aplicações inesperadas, e trabalhando nos detalhes, em 1982, a física Noble prêmio foi dado a Kenneth G. Wilson.

Retirado de " http://en.wikipedia.org/w/index.php?title=Renormalization&oldid=226641245 "

See also ebooksgratis.com: no banners, no cookies, totally FREE.