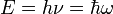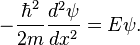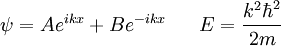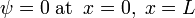Mecânica quântica

Mecânica quântica
Dualidade onda-partícula
Introdução Glossário · História
Fundo Notação Bra-ket A mecânica clássica Hamiltonian Interferência Velha teoria quântica
Conceitos fundamentais Complementaridade Decoherence Não-localidade Estado quântico Sobreposição Tunnelling Incerteza Função de onda
Experiências Desigualdade de Bell Davisson-Germer Escolha adiada apagador quântico Dupla fenda Franck-Hertz experimento Mach-Zehnder Inter. Elitzur-Vaidman Popper Borracha Quantum O gato de Schrödinger Stern-Gerlach Escolha retardada de Wheeler
Formulações Formulações Heisenberg Interação Mecânica matricial Schrödinger Soma de histórias Espaço de fase
Equações Dirac Klein-Gordon Pauli Rydberg Schrödinger
Interpretações Interpretações (Resumo) Causou-Consciousness Histórias consistentes Copenhague de Broglie-Bohm Conjunto Variáveis ocultas Muitos mundos Objetivo colapso Pondicherry Lógica quântica Relacional Stochastic Transacional
Tópicos avançados Caos quântico Teoria quântica de campos Ciência da informação quântica Teoria de espalhamento Mecânica quântica fracionários
Os cientistas Sino Blackett Bogolyubov Bohm Bohr Bardeen Nascido Bose de Broglie Compton Tanoeiro Dirac Dyson Davisson Duarte Debye Ehrenfest Einstein Everett Fock Fermi Feynman Hertz Heisenberg Hilbert Jordânia Klitzing Kusch Kramers von Neumann Pauli Cordeiro Laue Laughlin Moseley Millikan Onnes Planck Raman Rydberg Salam Schrödinger Störmer Shockley Schrieffer Shull Sommerfeld Thomson Tsui Tomonaga Weyl Enfermaria Wien Wigner Zeeman Zeilinger

Figo. 1: Densidades de probabilidade correspondente para o wavefunctions de um elétron em um átomo de hidrogénio possuindo definitiva energia (crescente para baixo: n = 1, 2, 3, ...) e o momento angular (crescente entre: s, p, d, ...). Áreas mais claras correspondem a mais elevada densidade de probabilidade para uma medição de posição. Wavefunctions como estes são directamente comparáveis com As figuras de Chladni de modos de vibração acústica na física clássica e são de fato modos de oscilação bem: eles possuem um forte energia e, portanto, uma aguçada freqüência. O momento angular e energia são quantizado, e apenas assumir valores discretos como aqueles mostrados (como é o caso de frequências ressonantes em acústica).

A mecânica quântica é o estudo da sistemas mecânicos cujas dimensões estão perto ou abaixo do atômica escala, tais como moléculas , átomos , elétrons , prótons e outros partículas subatômicas. A mecânica quântica é um ramo fundamental da física com amplas aplicações. A teoria quântica generaliza a mecânica clássica e fornece descrições precisas para muitos anteriormente inexplicável fenômenos como radiação de corpo negro e estável órbitas de elétrons. Os efeitos da mecânica quântica não são tipicamente observado em escalas macroscópicas, mas tornam-se evidentes no atômica e nível subatômico. No entanto, existem excepções a esta regra, como superfluidez.

Visão global

A palavra "quantum" veio da palavra latina que significa "como é grande" ou "quanto". Na mecânica quântica, ele se refere a uma unidade discreta que a teoria quântica atribui a certas quantidades físicas, tais como a energia de um átomo em repouso (veja a Figura 1, à direita). A descoberta de que ondas de energia têm pacotes discretos (chamada Quanta) que se comportam de um modo semelhante ao partículas levou ao ramo da física que lida com sistemas atômicas e subatômicas que nós hoje chamamos de mecânica quântica. É a base matemática quadro de muitos campos da física e da química , incluindo a física da matéria condensada , física do estado sólido, física atômica , física molecular , química computacional , química quântica , física de partículas , e da física nuclear . Os fundamentos da mecânica quântica foram estabelecidos durante a primeira metade do século XX por Werner Heisenberg, Max Planck , Louis de Broglie, Albert Einstein , Niels Bohr , Erwin Schrödinger, Max Born, John von Neumann , Paul Dirac , Wolfgang Pauli e outros. Alguns aspectos fundamentais da teoria ainda estão ativamente estudada.

A mecânica quântica é essencial para compreender o comportamento de sistemas em atômicas escalas de comprimento e menor. Por exemplo, se a mecânica newtoniana regido o funcionamento de um átomo, elétrons seria rapidamente viajar para e colidir com o núcleo , fazendo átomos estáveis impossível. No entanto, no mundo natural os elétrons normalmente permanecer em um caminho desconhecido orbital ao redor do núcleo, desafiando eletromagnetismo clássico.

A mecânica quântica foi inicialmente desenvolvido para proporcionar uma melhor explicação do átomo, especialmente o Os espectros de luz emitido por diferentes espécies atómicas . A teoria quântica do átomo foi desenvolvido como uma explicação para permanência do elétron em sua orbital, o que não poderia ser explicado pelas leis do movimento de Newton e por leis de Maxwell do eletromagnetismo clássico.

No formalismo da mecânica quântica, o estado de um sistema num dado momento é descrita por um complexo função de onda (por vezes referido como orbitais no caso de electrões atómicos), e mais geralmente, de um complexo de elementos de espaço vectorial . Este objeto matemático abstrato permite o cálculo de probabilidades de resultados de experimentos concretos. Por exemplo, ela permite calcular a probabilidade de encontrar um elétron em uma determinada região em torno do núcleo em um determinado momento. Ao contrário do que a mecânica clássica, nunca se pode fazer previsões simultâneas de variáveis conjugadas, tais como posição e momento, com precisão arbitrária. Por exemplo, os electrões podem ser considerados para ser localizada em algum lugar dentro de uma região do espaço, mas com as suas posições exactas ser desconhecido. Contornos de probabilidade constante, muitas vezes referida como "nuvens" pode ser desenhado em torno do núcleo de um átomo de conceituar onde o elétron pode ser localizado com a mais de probabilidade. Heisenberg princípio da incerteza quantifica a incapacidade de localizar com precisão a partícula.

O outro exemplar que levou a mecânica quântica foi o estudo de ondas eletromagnéticas tais como a luz. Quando foi encontrado em 1900 por Max Planck que a energia das ondas pode ser descrito como consistindo em pequenos pacotes ou quanta, Albert Einstein exploraram esta ideia para mostrar que uma onda electromagnética, tal como luz pode ser descrito por uma partícula denominada o fotão com um energia discreta dependente de sua freqüência. Isto levou a uma teoria da unidade entre partículas subatômicas e ondas eletromagnéticas chamados dualidade onda-partícula em que partículas e ondas não eram nem uma coisa nem outra, mas tinha certas propriedades de ambos. Embora a mecânica quântica descreve o mundo do muito pequeno, ele também é necessária para explicar certas " sistemas quânticos macroscópicos ", tais como os supercondutores e superfluidos.

Em termos gerais, a mecânica quântica incorpora quatro classes de fenômenos que a física clássica não pode ser responsável por: (i) a quantização (discretização) de certas quantidades físicas, (ii) dualidade onda-partícula , (iii) a O princípio da incerteza, e (iv) entrelaçamento quântico. Cada um destes fenómenos é descrita em pormenor nas secções subsequentes.

História

A história da mecânica quântica começou essencialmente com a descoberta de 1838 raios catódicos por Michael Faraday , a declaração de 1859 problema radiação de corpo negro por Gustav Kirchhoff, a sugestão de 1877 Ludwig Boltzmann que os estados de energia de um sistema físico podia ser discreta, e o 1900 hipótese quântica por Max Planck que nenhuma energia é irradiada e absorvida em quantidades divisíveis por "elementos de energia" discretas, E, de tal forma que cada um destes elementos de energia é proporcional ao ν frequência com a qual cada um deles individualmente irradiar energia , tal como definido pela seguinte fórmula:

onde h é Ação constante de Planck. Embora Planck insistiu que isso era simplesmente um aspecto da absorção e radiação de energia e não tinha nada a ver com a realidade física da própria energia, em 1905, para explicar a efeito fotoelétrico (1839), ou seja, aquela luz brilhante em determinados materiais podem funcionar para ejetar elétrons do material, Albert Einstein postulou, com base em hipótese quântica de Planck, que a luz em si consiste em quanta individual, que mais tarde veio a ser chamado de fótons (1926 ). De simples postulação de Einstein foi confirmada uma enxurrada de debates, teorizando e testes, e, assim, todo o campo da física quântica .

Relatividade e mecânica quântica

O mundo moderno da física está, nomeadamente, fundada em duas teorias testadas e comprovadamente som da Relatividade Geral ea Mecânica Quântica -theories que parecem contradizer-se. Os postulados que definem a teoria da relatividade ea teoria quântica, tanto de Einstein são, indiscutivelmente, apoiada pela evidência empírica rigorosa e repetida. No entanto, enquanto eles não se opõem diretamente entre si, teoricamente (pelo menos no que diz respeito às alegações primárias), eles são resistentes a serem incorporadas no prazo de um modelo coeso.

O próprio Einstein é bem conhecida por rejeitar algumas das reivindicações da mecânica quântica. Enquanto claramente inventiva neste campo, ele não aceitar as conseqüências mais filosóficas e interpretações da mecânica quântica, como a falta de determinista causalidade e a afirmação de que uma única partícula subatômica pode ocupar várias áreas de espaço ao mesmo tempo. Ele também foi o primeiro a notar algumas das conseqüências aparentemente exóticas de emaranhamento e os usou para formular o Paradoxo Einstein-Podolsky-Rosen, na esperança de mostrar que a mecânica quântica tem implicações inaceitáveis. Esta foi 1935, mas em 1964 ele foi mostrado por John Bell (ver Desigualdade de Bell) essa suposição de Einstein de que a mecânica quântica é correta, mas tem que ser completado por variáveis ocultas, foi baseada em suposições filosóficas erradas: de acordo com o papel de J. Bell eo Interpretação de Copenhague (a interpretação comum da mecânica quântica pelos físicos durante décadas), e contrariamente às idéias de Einstein, a mecânica quântica é

• nem uma teoria "realista" (desde que as medições quânticas não indicam propriedades pré-existentes, mas sim se preparam propriedades)

• nem teoria local (essencialmente não, porque o vetor de estado determina simultaneamente as amplitudes de probabilidade em todos os locais, ).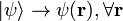

O paradoxo Einstein-Podolsky-Rosen mostra em qualquer caso, que não existem experiências pelas quais se pode medir o estado de uma partícula e instantaneamente modificar o estado do seu parceiro emaranhados, embora as duas partículas pode ser uma distância arbitrária separados; no entanto, este efeito não viola causalidade, uma vez que nenhuma transferência de informações acontece. Estas experiências são a base de algumas das aplicações mais tópicas da teoria, criptografia quântica, que funciona bem, embora em pequenas distâncias tipicamente 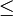1000 km, de estar no mercado desde 2004.

Não fazer existir teorias quânticas que incorporam exemplo relatividade especial-para, eletrodinâmica quântica (QED), que é atualmente a teoria física mais precisamente testado -e estes estão no coração da moderna física de partículas . A gravidade é desprezível em muitas áreas da física de partículas, de modo que a unificação entre a relatividade geral ea mecânica quântica não é uma questão urgente nesses aplicativos. No entanto, a ausência de uma teoria da correcta gravitação quântica é uma questão importante na cosmologia .

As tentativas de uma teoria unificada

Inconsistências surgem quando se tenta juntar as leis quânticas com a relatividade geral , uma descrição mais elaborada de espaço-tempo que incorpora gravitação . Resolvendo essas inconsistências tem sido um dos principais objetivos do XX - e vigésimo primeiro -century física. Muitos físicos proeminentes, incluindo Stephen Hawking , têm trabalhado na tentativa de descobrir um " Grande Unificação Theory ", que combina não só diferentes modelos de física subatômica, mas também deriva quatro forças do universo-o força forte, eletromagnetismo , força fraca e gravidade - a partir de uma única força ou fenômeno.

A mecânica quântica e da física clássica

As previsões da mecânica quântica foram verificados experimentalmente para um grau muito elevado de precisão. Assim, a lógica de corrente princípio da correspondência entre a mecânica clássica e quântica é que todos os objetos de obedecer às leis da mecânica quântica, mecânica clássica e está apenas a mecânica quântica de sistemas de grande porte (ou um estatísticos mecânica quântica de uma grande coleção de partículas). Leis da mecânica clássica seguir assim de leis da mecânica quântica no limite de sistemas grandes ou grandes números quânticos.

Principais diferenças entre as teorias clássica e quântica já foram mencionados acima, nas observações sobre a Paradoxo Einstein-Podolsky-Rosen. Essencialmente, a diferença resume-se à afirmação de que a mecânica quântica é coerente (adição de amplitudes), enquanto teorias clássicas são incoerentes (adição de intensidades). Assim, essas quantidades como comprimentos de coerência e de coerência vezes entram em jogo. Para os organismos microscópicos a extensão do sistema é, certamente, muito menor do que o comprimento de coerência; para corpos macroscópicos espera-se que ele deve ser o contrário.

Isto está de acordo com as observações seguintes:

Muitas propriedades "macroscópicas" dos sistemas "clássicos" são conseqüências diretas do comportamento quântico de suas partes. Por exemplo, a estabilidade da matéria a granel (que consiste em átomos e moléculas que rapidamente entrar em colapso sob forças eléctricas sozinho), rigidez desta questão, propriedades ópticas e magnéticos deste mecânica, térmica, química, a matéria-eles são todos os resultados da interacção de cargas elétricas sob as regras da mecânica quântica.

Enquanto comportamento aparentemente exótica de matéria posta pela mecânica quântica ea teoria da relatividade tornou mais evidente quando se lida com extremamente veloz ou partículas extremamente pequenas, as leis da física clássica "newtoniano" ainda permanecem precisos em prever o comportamento do ambiente ("grande") -objetos da ordem do tamanho das moléculas grandes e maior-a velocidades muito menor do que a velocidade da luz.

Teoria

Existem inúmeras formulações matematicamente equivalentes da mecânica quântica. Uma das formulações mais antigo e mais usado é o teoria da transformação proposta por Cambridge físico teórico Paul Dirac , que unifica e generaliza as duas primeiras formulações da mecânica quântica, mecânica matricial (inventado por Werner Heisenberg) e mecânica ondulatória (inventado por Erwin Schrödinger).

Nesta formulação, o estado instantâneo de um sistema quântico codifica as probabilidades de suas propriedades mensuráveis, ou " observáveis ". Exemplos de observáveis incluem energia , posição, momentum, e momento angular . Observáveis pode ser contínua (por exemplo, a posição de uma partícula) ou discreta (por exemplo, a energia de um electrão ligado a um átomo de hidrogénio).

Geralmente, a mecânica quântica não atribuir valores definitivos para observáveis. Em vez disso, ele faz previsões sobre distribuições de probabilidade ; isto é, a probabilidade de obtenção de cada um dos possíveis resultados de medição de um observável. Naturalmente, estas probabilidades dependerá do estado quântico no instante da medição. Existem, no entanto, certos estados que estão associados a um valor definido de um determinado observável. Estes são conhecidos como "auto-estados" do observável ("eigen" pode ser aproximadamente traduzido do alemão como inerente ou como uma característica). No mundo todos os dias, é natural e intuitivo pensar em tudo estar em um auto-estado de cada observável. Tudo parece ter uma posição definitiva, um momento definido, e um tempo definido de ocorrência. No entanto, a mecânica quântica não identificar os valores exatos para a posição ou momento de uma determinada partícula em um determinado espaço em um tempo finito; em vez disso, ele apenas fornece uma gama de probabilidades de onde essa partícula pode ser. Portanto, tornou-se necessário o uso de palavras diferentes para (a) o estado de algo que tem uma relação de incerteza e (b) um estado que tem um valor definitivo. Este último é chamado de "auto-estado" da propriedade que está sendo medido.

Por exemplo, considere um partícula livre. Em mecânica quântica, há dualidade onda-partícula de modo que as propriedades da partícula pode ser descrito como uma onda. Portanto, a sua estado quântico pode ser representada como uma onda , de forma arbitrária e que se prolonga sobre a totalidade do espaço, chamado de função de onda. A posição eo momento da partícula são observáveis. O Princípio A incerteza da mecânica quântica afirma que a posição e o impulso não podem, simultaneamente, ser conhecido com precisão infinita, ao mesmo tempo. No entanto, pode-se medir apenas a posição sozinho de uma partícula em movimento livre a criação de um auto-estado de posição com uma função de onda que é muito grande em uma determinada posição x, e quase zero em qualquer outro lugar. Se se executa uma medição posição sobre a referida função de onda, o resultado será obtido x com quase 100% de probabilidade. Em outras palavras, a posição da partícula livre irá ser quase conhecido. Isso é chamado de uma auto-estado de posição (matematicamente mais preciso: a eigenstate generalizada ( eigendistribution)). Se a partícula for uma autoestado em posição de, em seguida, o seu movimento é completamente desconhecido. Um autoestado de impulso, por outro lado, tem a forma de um onda plana. Pode ser mostrado que o comprimento de onda é igual a h / p, em que h é P constante e de Planck é a dinâmica da auto-estado . Se a partícula está em uma auto-estado de impulso, em seguida, a sua posição é completamente desfocado.

Normalmente, um sistema não estará em um auto-estado de qualquer observável estamos interessados em. No entanto, se mede o observável, a função de onda vai instantaneamente ser um auto-estado (ou eigenstate generalizada) de que está sendo observado. Este processo é conhecido como colapso da função de onda. Ela envolve a expansão do sistema em estudo para incluir o dispositivo de medição, de modo que um cálculo detalhado quântica já não seria viável e uma descrição clássica deve ser utilizado. Se se conhece a função no instante antes da medição de onda correspondente, um será capaz de calcular a probabilidade de colapso em cada um dos possíveis autoestados. Por exemplo, a partícula livre no exemplo anterior terá geralmente uma função de onda que é um pacote de ondas centrado em torno de uma posição x _0, nem um auto-estado de posição nem do momento significa. Quando se mede a posição da partícula, é impossível prever com certeza o resultado que vai obter. É provável, mas não determinado, que será próximo x _0, em que a amplitude da função de onda é grande. Após a medição é realizada, tendo obtido algum resultado x, a função de onda colapsa em uma eigenstate posição centrada em x.

Funções de onda pode mudar à medida que o tempo avança. Uma equação conhecida como a Equação de Schrödinger descreve como funções de onda mudar com o tempo, um papel semelhante ao da segunda lei de Newton na mecânica clássica. A equação Schrödin, aplicado ao exemplo da partícula livre acima mencionado, prevê que o centro de um pacote de ondas irá mover-se através do espaço a uma velocidade constante, como uma partícula clássica sem forças que actuam sobre ele. No entanto, o pacote de ondas também irá espalhar-se medida que o tempo progride, o que significa que a posição torna-se mais incerta. Isto também tem o efeito de tornar autoestados posição (que pode ser pensada como infinitamente pacotes de ondas agudas) para pacotes de onda alargado que não são autoestados posição mais longos.

Algumas funções de onda produzir distribuições de probabilidades que são constantes no tempo. Muitos sistemas que são tratados de forma dinâmica na mecânica clássica são descritos por tais funções de onda "estáticas". Por exemplo, um único electrão não excitado em um átomo é representado classicamente como uma partícula em movimento numa trajectória circular em torno do núcleo atómico , enquanto que na mecânica quântica é descrita por, um estático simetria esférica função de onda em torno do núcleo ( Fig. 1 ). (Note que apenas os estados mais baixos do momento angular, s marcados, são esfericamente simétrica).

A evolução temporal das funções de onda é determinista no sentido de que, dado uma função de onda num momento inicial, ele faz uma previsão definitiva de que a função de onda será, em qualquer momento posterior. Durante um medição, a alteração da função de onda para outra não é determinista, mas bastante imprevisível, isto é, aleatória.

O probabilística natureza da mecânica quântica vem, então, o ato de medição. Este é um dos aspectos mais difíceis de sistemas quânticos para entender. Ele foi o tema central na famosa Bohr-Einstein debates, em que os dois cientistas tentaram esclarecer estes princípios fundamentais por meio de experiências de pensamento. Nas décadas após a formulação da mecânica quântica, a questão do que constitui uma "medida" tem sido amplamente estudado. Interpretações da mecânica quântica foram formulados para acabar com o conceito de "colapso da função de onda"; ver, por exemplo, a interpretação estado relativo. A ideia básica é que, quando um sistema quântico interage com um aparelho de medição, as respectivas funções de onda tornar emaranhados, de modo que o sistema quântico inicial deixa de existir como uma entidade independente. Para mais detalhes, consulte o artigo sobre medição na mecânica quântica.

Formulação matemática

Na formulação matematicamente rigorosa da mecânica quântica, desenvolvido por Paul Dirac e John von Neumann , os estados possíveis de um sistema mecânico quântico são representados por vetores unitários (chamados "vetores de estado") que residem em um complexo separável Espaço de Hilbert (variadamente chamado de "espaço de estado" ou o "espaço associado Hilbert" do sistema) bem definida até um número complexo da norma 1 (o fator de fase). Em outras palavras, os estados possíveis são pontos na projectivization de um espaço de Hilbert. A natureza exacta deste espaço de Hilbert é dependente do sistema; por exemplo, o espaço de estados para a posição eo momento estados é o espaço de funções de quadrado integrável, enquanto o espaço de estado para o spin de um único próton é apenas o produto de dois aviões complexos. Cada observável é representado por um maximally- Hermitiano (precisamente: por um auto-adjunta) linear operador que actua sobre o espaço de estado. Cada autoestado de um observáveis corresponde a um vector próprio do operador, e o associado valor próprio correspondente ao valor do observável em que autoestado. Se espectro do operador é discreto, o observável apenas pode atingir esses autovalores discretos.

A evolução no tempo de um estado quântico é descrito pela Schrödin equação, em que o Hamiltoniano, o operador que corresponde à energia total do sistema, gera evolução temporal.

O produto interno entre dois vectores de estado é um número conhecido como um complexo amplitude de probabilidade. Durante a medição, a probabilidade de que um sistema colapsa a partir de um dado estado inicial para um autoestado particular é dado pelo quadrado do valor absoluto das amplitudes de probabilidade entre os estados iniciais e finais. Os possíveis resultados de uma medição são os valores próprios do operador - o que explica a escolha dos operadores hermitianas, para o qual todos os valores próprios são reais. Podemos encontrar a distribuição de probabilidade de um observável em um determinado estado, calculando a decomposição espectral do operador correspondente. Heisenberg O princípio da incerteza é representado pela afirmação de que os operadores correspondentes a determinados observáveis não fazer comutar.

A equação de Schrödinger atua sobre toda a amplitude de probabilidade, e não apenas seu valor absoluto. Considerando que o valor absoluto da amplitude de probabilidade codifica a informação sobre as probabilidades, o seu fase codifica informações sobre o interferência entre estados quânticos. Isto dá origem ao comportamento de estados quânticos de onda.

Acontece que soluções analíticas da equação de Schrödinger só estão disponíveis para um pequeno número de modelo Hamiltonianas, dos quais o oscilador harmônico quântico, o de partícula dentro de uma caixa, a ião molecular de hidrogénio e o átomo de hidrogénio são os representantes mais importantes. Até mesmo o hélio átomo, que contém apenas mais um elétron de hidrogênio, desafia todas as tentativas de um tratamento totalmente analítica. Existem várias técnicas para a geração de soluções aproximados. Por exemplo, no método conhecido como teoria uma perturbação utiliza os resultados analíticos para um modelo de mecânica quântica simples para gerar resultados para um modelo mais complexo relacionado com o modelo simples através de, por exemplo, a adição de uma fraco energia potencial. Outro método é a "equação semi-clássico de movimento" abordagem, que se aplica aos sistemas para os quais a mecânica quântica produz desvios fracos de comportamento clássico. Os desvios podem ser calculados com base no movimento clássica. Esta abordagem é importante para o campo de caos quântico.

Uma formulação alternativa da mecânica quântica é Feynman 's caminho formulação integrante, em que uma amplitude de mecânica quântica é considerado como uma soma de histórias entre estados inicial e final; este é o homólogo do quantum-mecânica de princípios de ação na mecânica clássica.

Interações com outras teorias científicas

As regras fundamentais da mecânica quântica são muito amplas. Afirmam que o espaço de estado de um sistema é um Espaço de Hilbert e os observáveis são Operadores hermitianas agindo em que o espaço, mas não nos dizem que os utilizadores do espaço Hilbert ou que, ou se ele ainda existe. Estes devem ser escolhidos de forma adequada, a fim de se obter uma descrição quantitativa de um sistema quântico. Um guia importante para fazer essas escolhas é o princípio de correspondência, que afirma que as previsões da mecânica quântica reduzir para aqueles da física clássica quando um sistema se move para energias mais altas ou equivalentemente, números quânticos maiores. Em outras palavras, a mecânica clássica é simplesmente uma mecânica quântica de sistemas de grande porte. Este limite "alta energia" é conhecido como o limite clássico ou correspondência. Por conseguinte, pode-se iniciar a partir de um modelo clássico estabelecida de um sistema particular, e tentar adivinhar o modelo quântico subjacente que dá origem ao modelo clássico no limite de correspondência

Quando a mecânica quântica foi originalmente formulada, foi aplicada a modelos cuja correspondência limite era de não-relativística mecânica clássica . Por exemplo, o modelo do bem conhecido oscilador harmónico quântico utiliza uma expressão explícita não relativística para a energia cinética do oscilador, e é assim uma versão do quantum oscilador harmônico clássica.

As primeiras tentativas de fundir a mecânica quântica com a relatividade especial envolveu a substituição da equação de Schrödinger com uma equação covariant como a Equação de Klein-Gordon ou o Equação de Dirac. Enquanto essas teorias foram bem sucedidos em explicar muitos resultados experimentais, eles tinham certas qualidades insatisfatórias decorrentes de sua negligência da criação relativista e aniquilação de partículas. A teoria quântica relativística totalmente exigiu o desenvolvimento de teoria quântica de campos , que se aplica a um campo de quantização, em vez de um conjunto fixo de partículas. A primeira teoria quântica de campos completo, eletrodinâmica quântica, fornece uma descrição totalmente quântico da interação eletromagnética .

O aparelho cheio de teoria quântica de campos é muitas vezes desnecessário para descrever sistemas de eletrodinâmica. Uma abordagem mais simples, uma empregada desde o início da mecânica quântica, é tratar carregadas partículas como objetos quânticos sendo acionados por um campo eletromagnético clássico. Por exemplo, o modelo do quantum elementar átomo de hidrogénio descreve o campo eléctrico do átomo de hidrogénio, usando um clássico 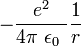Potencial de Coulomb. Esta abordagem "semi-clássico" falha se as flutuações quânticas no campo eletromagnético desempenhar um papel importante, como na emissão de fótons por partículas carregadas.

Teorias quânticas de campo para o força nuclear forte ea força nuclear fraca têm sido desenvolvidos. A teoria quântica de campos de força nuclear forte é chamado cromodinâmica quântica, e descreve as interações das partículas subnucleares: quarks e glúons. O força nuclear fraca ea força eletromagnética foram unificadas, em suas formas quantificados, em uma única teoria do campo quântico conhecido como teoria eletrofraca.

Ele provou difícil construir modelos quânticos de gravidade , os restantes força fundamental. Aproximações semi-clássicos são viáveis, e levaram a previsões, como a radiação de Hawking . No entanto, a formulação de uma teoria completa de gravitação quântica é prejudicado por aparentes incompatibilidades entre a relatividade geral , a teoria mais precisa da gravidade atualmente conhecida, e alguns dos pressupostos fundamentais da teoria quântica. A resolução dessas incompatibilidades é uma área de pesquisa ativa, e as teorias, como a teoria das cordas estão entre os possíveis candidatos para uma futura teoria da gravidade quântica.

Derivação de quantização

A partícula em uma caixa de energia potencial 1-dimensional é o exemplo mais simples, onde as restrições para levar a quantização de níveis de energia. A caixa é definido como zero de energia potencial dentro de um determinado intervalo de tempo e infinito em todos os lugares fora desse intervalo. Para o caso 1-dimensional no 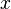direcção, a equação de Schrödinger independente do tempo pode ser escrito como:

As soluções gerais são:

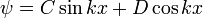( reescrita exponencial)

A presença das paredes da caixa restringe as soluções aceitáveis para a função de onda. Em cada parede:

Considere x = 0

• pecado 0 = 0, cos 0 = 1. Para satisfazer 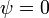D = 0 (COS termo é removido)

Agora, considere:

• em que X = G,
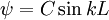
• Se C = 0 então 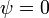para todos os x e entraria em conflito com a interpretação Nascido
• portanto, o pecado kL devem ser satisfeitas por

Nesta situação, n deve ser um número inteiro, mostrando a quantização dos níveis de energia.

Aplicações

A mecânica quântica teve enorme sucesso em explicar muitas das características do nosso mundo. O comportamento individual das partículas subatômicas que compõem todas as formas de matéria - elétrons , prótons , nêutrons , fótons e outros muitas vezes pode-descrita apenas ser satisfatoriamente usando a mecânica quântica. A mecânica quântica foi fortemente influenciado a teoria das cordas , um candidato a um teoria de tudo (ver reducionismo). Ele também está relacionada com a mecânica estatística .

A mecânica quântica é importante para a compreensão de como os átomos individuais combinam covalentemente para formar produtos químicos ou moléculas. A aplicação da mecânica quântica para a química é conhecida como química quântica . Mecânica (Relativistic) quânticos podem, em princípio, matematicamente descrever mais da química. A mecânica quântica pode fornecer uma visão quantitativa em processos de ligação iônicos e covalentes por explicitamente mostrando que as moléculas são energeticamente favorável a que os outros, e por cerca de quanto. A maioria dos cálculos realizados em química computacional contar com a mecânica quântica.

Grande parte da moderna tecnologia opera em uma escala onde os efeitos quânticos são significativos. Exemplos incluem o de laser , o transistor, o microscópio eletrônico, e ressonância magnética. O estudo de semicondutores levou à invenção do e o diodo transistor, que são indispensáveis para modernos eletrônica .

Os investigadores estão actualmente a procurar métodos robustos de manipular diretamente os estados quânticos. Esforços estão sendo feitos para desenvolver criptografia quântica, o que permitirá garantida a transmissão segura de informações . Um objetivo mais distante é o desenvolvimento de computadores quânticos , que são esperados para executar determinadas tarefas computacionais exponencialmente mais rápido do que clássicos computadores . Outro tema de pesquisa ativo é teletransporte quântico, que trata de técnicas para transmitir estados quânticos em distâncias arbitrárias.

Em muitos dispositivos, mesmo o simples interruptor, tunelamento quântico é vital, pois caso contrário, os elétrons da corrente elétrica não poderia penetrar a barreira potencial constituído, no caso de o interruptor de luz, de uma camada de óxido. Chips de memória flash encontrado em Drives USB também usar tunelamento quântico para apagar suas células de memória.

Conseqüências filosóficas

Desde a sua criação, os muitos resultados contra-intuitiva da mecânica quântica têm provocado forte filosófico debate e muitos interpretações. Mesmo questões fundamentais, tais como Regras básicas de Max Born relativas amplitudes de probabilidade e distribuições de probabilidade levou décadas para ser apreciado.

O Interpretação de Copenhague, em grande parte devido ao físico teórico dinamarquês Niels Bohr , é a interpretação da mecânica quântica mais amplamente aceita entre os físicos. De acordo com ele, a natureza probabilística da mecânica quântica previsões não podem ser explicados em termos de alguma outra teoria determinista, e não simplesmente refletem nosso conhecimento limitado.A mecânica quântica forneceprobabilísticosresultados, porque o universo físico é a própria probabilístico em vez dedeterminista.

Albert Einstein não gostava dessa perda de determinismo na medição. (Daí sua famosa frase "Deus não joga dados com o universo.") Ele declarou que deve haver uma locais teoria variável mecânica quântica subjacente escondidos e, consequentemente, a presente teoria estava incompleta. Em retaliação do dogma religioso aparentemente ele produziu uma série de objeções à teoria, o mais famoso dos quais se tornou conhecido como o paradoxo EPR. Existem suspeitas de que a mecânica quântica foi criada para ser confuso e difícil de refutar, a fim de dar aos cientistas menor a chance de entrar para a história ao lado de Einstein. John Bell mostrou que o paradoxo EPR ​​levou a experimentalmente testáveis ​​diferenças entre a mecânica quântica e as teorias locais. experiências cujos validades são altamente questionada foram tomadas como uma confirmação de que a mecânica quântica é correta eo mundo real devem ser descritos em termos de teorias não-locais.

O escritor CS Lewis viram mecânica quântica como incompleta, porque as noções de indeterminismo não concordava com suas crenças religiosas. Lewis, professor de Inglês, era da opinião de que o princípio da incerteza de Heisenberg foi mais de uma limitação epistêmica do que uma indicação de indeterminação ontológica, ea este respeito acreditava semelhante a muitos defensores de teorias variáveis ​​ocultas. O Bohr-Einstein debates proporcionar uma vibrante crítica da interpretação de Copenhaga a partir de um ponto de vista epistemológico.

O Everett interpretação de muitos mundos, formulado em 1956, afirma que todas as possibilidades descritas pela teoria quântica ocorrer simultaneamente em um " multiverso ", composto de universos paralelos na sua maioria independentes. Isto não é conseguido através da introdução de uma nova axioma para mecânica quântica, mas, pelo contrário, por remoção do axioma do colapso do pacote de ondas: Todas as possíveis estados consistentes de o sistema de medição e o aparelho de medição (incluindo o observador) estão presentes em um verdadeiro físico (e não apenas formalmente matemática, como em outras interpretações) superposição quântica. (Essa superposição de combinações estado consistente de sistemas diferentes é chamada de estado emaranhado.) Enquanto o multiverso é determinística, percebemos comportamento não-determinístico regido por probabilidades, porque podemos observar somente o universo, ou seja, a contribuição estado consistente com a mencionada superposição, que habitamos. A interpretação de Everett é perfeitamente consistente com as experiências de John Bell e torna-los intuitivamente compreensível. No entanto, de acordo com a teoria da decoerência quântica, os universos paralelos nunca será acessível para nós. Esta inacessibilidade pode ser entendida do seguinte modo: uma vez por medição é feita, o sistema de medida se torna enredado com tanto o físico que mediu e um grande número de outras partículas, algumas das quais são fotões que voam afastado para a outra extremidade do universo; a fim de provar que a função de onda não entrou em colapso um teria que trazer todas estas partículas para trás e medi-los de novo, juntamente com o sistema que foi medido inicialmente. Isto é completamente impraticável, mas mesmo que um pode, teoricamente, fazer isso, ele iria destruir qualquer evidência de que a medida original teve lugar (incluindo a memória do físico).