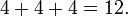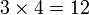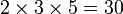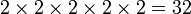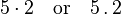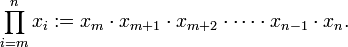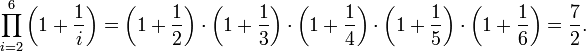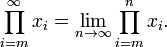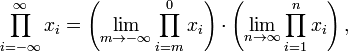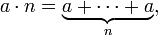Multiplicación
Acerca de este escuelas selección Wikipedia
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Una rápida conexión para el apadrinamiento de niños es http://www.sponsor-a-child.org.uk/
Multiplicación de números enteros es el operación matemática de la suma de múltiples copias del mismo número. Por ejemplo, cuatro multiplicado por tres es doce, ya que tres grupos de cuatro hacen doce:
Multiplicación también se puede ver como objetos de conteo dispuestos en una rectángulo, o encontrar el área del rectángulo cuyos lados han dado longitudes.
La multiplicación es una de las cuatro operaciones principales en la aritmética elemental , y la mayoría de las personas aprenden de multiplicación básicas algoritmos en escuela primaria. La inversa de la multiplicación es la división .
La multiplicación se generaliza a muchos tipos de números y constructos más abstractos tales como matrices.
Notación y terminología
Multiplicación está escrito utilizando el signo de multiplicación "x" entre los términos; es decir, en notación infija. El resultado se expresa con una signo igual. Por ejemplo,
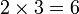(Verbalmente, "dos veces tres es igual a seis")
Hay varias otras notaciones comunes para la multiplicación:
- Multiplicación veces se denota por ya sea una punto medio o una período:
- La asterisco (por ejemplo, 5 * 2) se utiliza a menudo con los ordenadores, ya que aparece en cada teclado. Este uso se originó en el Lenguaje de programación FORTRAN.
- En álgebra , la multiplicación participación las variables se escriben a menudo como un yuxtaposición (por ejemplo xy de x por y o 5 x de cinco veces x). Esta notación se puede utilizar también para los números que están rodeados por paréntesis (por ejemplo, 5 (2) o (5) (2) para cinco veces dos).
Los números que se multiplican generalmente se llaman los "factores" o "multiplicandos". Al pensar en la multiplicación como suma repetida, el número que se repite se llama el "multiplicando", mientras que el número de repeticiones se llama el "multiplicador". En álgebra, un número que se multiplica por una variable o expresión (es decir, el 3 en 3 xy 2) se llama coeficiente.
El resultado de una multiplicación se llama producto, y es una múltiplo de cada factor. Por ejemplo 15 es el producto de 3 y 5, y es a la vez un múltiplo de 3 y un múltiplo de 5.
Cálculo
Los métodos estándar para multiplicar números con lápiz y papel requieren un tabla de multiplicar de productos memorizados o consultadas de un pequeño número (normalmente dos números del 0 al 9), sin embargo un método, el algoritmo de la multiplicación campesina, no lo hace. Muchos planes de estudio de matemáticas desarrollado de acuerdo con los estándares del 1989 NCTM no enseñan métodos aritméticos estándar, en lugar guiar a los estudiantes a inventar sus propios métodos de cálculo. Aunque ampliamente adoptado por muchos distritos escolares en países como los Estados Unidos, se han encontrado con la resistencia de algunos padres y matemáticos, y algunos distritos han abandonado desde dichos planes de estudio a favor de matemáticas tradicionales.
Multiplicar números para más de un par de decimales a mano es tedioso y propenso a errores. Logaritmos comunes fueron inventados para simplificar estos cálculos. La regla de cálculo permitió que los números que se multiplican rápidamente a cerca de tres lugares de precisión. A partir de principios del siglo XX , mecánicos calculadoras , como el Marchant, multiplicación automática de hasta 10 dígitos. Electrónicos modernos ordenadores y calculadoras han reducido en gran medida la necesidad de la multiplicación por la mano.
Algoritmos Históricos
Los métodos de multiplicación se documentaron en el Egipto , Grecia , Babilonia , del valle del Indo , y chinos civilizaciones.
Egipcios
El método egipcio de multiplicación de números enteros y fracciones, documentado en el Papiro de Ahmes, era por adiciones sucesivas y duplicación. Por ejemplo, para encontrar el producto de 13 y 21 uno tuvo que duplicar 21 tres veces, obteniendo 1 × 21 = 21, 2 × 21 = 42, 4 × 21 = 84, 8 × 21 = 168. El producto completo, entonces podría ser encontrado añadiendo los términos apropiados que se encuentran en la secuencia de duplicación:
- 13 × 21 = (1 + 4 + 8) x 21 = (1 × 21) + (4 x 21) + (8 × 21) = 21 + 84 + 168 = 273.
Babilonios
Los babilonios usaban un sexagésimo sistema de numeración posicional, análoga a la de hoy en día sistema decimal. Por lo tanto, la multiplicación de Babilonia era muy similar al moderno multiplicación decimal. Debido a la relativa dificultad de recordar 60 × 60 productos diferentes, los matemáticos babilonios emplearon tablas de multiplicar. Estas tablas consistían en una lista de los veinte primeros múltiplos de un cierto número principal n: n, n 2, ..., 20 n; seguido por los múltiplos de 10 n: 30 n 40 n, y 50 n. Luego de calcular cualquier producto sexagesimal, digamos 53 n, uno sólo necesita añadir 50 n y 3 n calculado a partir de la tabla.
Chino
En los libros, Chou Pei Suan Ching fecha anterior a 300 antes de Cristo, y la Nueve capítulos del arte matemático, los cálculos de multiplicación fueron escritos en palabras, aunque los primeros matemáticos chinos emplean un ábaco en cálculos manuales de suma y multiplicación.
Valle del Indo
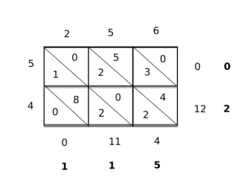
Los matemáticos hindúes tempranos de la región del valle del Indo utilizan una variedad de trucos intuitivas para realizar la multiplicación. La mayoría de los cálculos se realizaron en pequeñas tabletas de pizarra de la mano, el uso de tablas de tiza. Una técnica era la de multiplicación de celosía (o multiplicación gelosia). Aquí una tabla se ha elaborado con las filas y columnas etiquetadas por los multiplicandos. Cada caja de la tabla se divide diagonalmente en dos, como un triangular celosía. Las entradas de la tabla conserven los productos parciales, escritos como números decimales. El producto podría entonces estar formada sumando abajo las diagonales del enrejado.
Método moderno
El método moderno de la multiplicación basado en el Numeración arábiga fue descrita por primera vez por Brahmagupta. Brahmagupta dio reglas para la suma, resta, multiplicación y división. Henry Burchard Bien, entonces profesor de Matemáticas en la Universidad de Princeton , escribió lo siguiente:
- Los indios son los inventores no sólo del sistema decimal posicional en sí, sino de la mayoría de los procesos involucrados en ajustar cuentas primaria con el sistema. Suma y resta actuaron bastante ya que se realizan hoy en día; multiplicación en que hayan realizado en muchos aspectos, entre ellos el nuestro, pero la división que hicieron cumbrously.
Artículos de secuencias
Notación pi capital
El producto de una secuencia de términos se puede escribir con el símbolo de producto, que se deriva de la capital carta Π (pi) en el alfabeto griego . Posición Unicode U + 220F (Π) se define un producto ary n para este propósito, distinta de U + 03A0 (Π), la carta. Este se define como:
El subíndice da el símbolo para una variable dummy (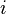 
en nuestro caso) y su valor más bajo ( 
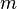); el superíndice da su valor superior. Así, por ejemplo:
En caso de que m = n, el valor del producto es el mismo que el de el factor x m. Si m> n, el producto es el vacío producto, con el valor 1.
Productos Infinite
Uno puede también considerar los productos de un número infinito de términos; estos son llamados productos infinitos. Notacionalmente, queremos sustituir n por encima de la lemniscata (símbolo del infinito) ∞. En los reales, el producto de una serie de este tipo se define como el límite del producto de la primera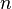 
términos, como 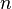crece sin límite. Esto es, por definición,
Uno puede sustituir de manera similar 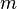con infinito negativo, y definir:
siempre que existan ambos límites.
Interpretación
Producto cartesiano
La definición de la multiplicación como repetida además proporciona una manera de llegar a una interpretación teoría de conjuntos de multiplicación de números cardinales . En la expresión
si los n copias de una se van a combinar en unión de la desunión entonces es claro que se deben hacer disjuntos; una forma obvia de hacer esto es utilizar una o n como la indexación fijado para el otro. Luego, los miembros del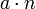 
son exactamente los de la Producto cartesiano 
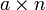. Las propiedades de la operación multiplicativa que se aplica a los números naturales, entonces siguen trivialmente de las propiedades correspondientes del producto cartesiano.
Propiedades
Para enteros, fracciones, reales y números complejos, la multiplicación tiene ciertas propiedades:
- Propiedad conmutativa
- El orden en el que dos números se multiplican, no importa.
- x · y = y · x.
- Propiedad asociativa
- Los problemas que implican únicamente la multiplicación son invariantes respecto de orden de las operaciones.
- (X · y) · z = x · (y · z).
- Propiedad distributiva
- Sostiene con respecto a la adición sobre la multiplicación. Esta identidad es de primordial importancia en la simplificación de expresiones algebraicas.
- x · (y + z) = x · y + x · z.
- Elemento de identidad
- de la multiplicación es 1; nada multiplicado por uno es en sí mismo. Esto se conoce como la propiedad de identidad
- x · 1 = x.
- Elemento cero
- Cualquier cosa multiplicado por cero es cero. Esto se conoce como la propiedad cero de la multiplicación.
- x · 0 = 0
- Propiedad Inversa
- Cada número x, excepto cero, tiene un inverso multiplicativo, 1 / x, tal que x · (1 / x) = 1.
- Preservación Orden
- La multiplicación por un número positivo preserva orden: si a> 0, entonces si b> c, entonces a · b> a · c. La multiplicación por un número negativo invierte orden: si a <0, entonces si b> c, entonces a · b <a · c.
- Negativo una veces cualquier número es igual al negativo de ese número.
- (-1) · X = (- x)
- Negativo una veces uno negativo es positivo.
- (-1) · (-1) = 1
Otros sistemas matemáticos que incluyen una operación de multiplicación pueden no tener todas estas propiedades. Por ejemplo, la multiplicación no, en general, conmutativa para las matrices y es cuaterniones.
Pruebas
No todas estas propiedades son independientes; algunos son una consecuencia de los otros. Una propiedad que puede ser probada de los demás es la propiedad cero de la multiplicación. Está comprobado por medio de la propiedad distributiva. Asumimos todas las propiedades habituales de suma y resta, y - x significa lo mismo que
.
- x · 0
- = (X · 0) + x - x
- = (X · 0) + (x · 1) - x
- = X · (0 + 1) - x
- = (X · 1) - x
- = X - x
- = 0.
Así que hemos demostrado:
- x · 0 = 0.
La identidad (-1) · x = (- x) también se puede probar usando la propiedad distributiva:
- (-1) · X
- = (-1) · X + x - x
- = (-1) · X + 1 · x - x
- = (-1 + 1) · x - x
- = 0 · x - x
- = 0 - x
- = - X
La prueba de que (-1) · (-1) = 1 es ahora fácil:
- (-1) · (-1)
- = - (- 1)
- = 1.
Multiplicación con los axiomas de Peano
- En el libro Arithmetices principia, exposita nova methodo, Giuseppe Peano propuso un nuevo sistema para la multiplicación sobre la base de sus axiomas para los números naturales.
- a × 1 = a
- a × b '= (a × b) + a
- Aquí, b 'representa el sucesor de b, o el número natural que sigue b. Con la otra nueve axiomas, es posible probar las normas comunes de la multiplicación, como las propiedades distributivas o asociativos.
Multiplicación con la teoría de conjuntos
Es posible, aunque difícil, para crear una definición recursiva de la multiplicación con la teoría de conjuntos. Tal sistema general se basa en la definición de Peano de la multiplicación.
Multiplicación en la teoría de grupos
Es fácil demostrar que hay un grupo de multiplication- los números racionales no cero. Multiplicación con las satisface números distintos de cero
- Cierre - para todos los A y B en el grupo, a × b está en el grupo.
- Asociatividad - Esto es sólo la propiedad asociativa: (a × b) × c = a × (b × c)
- Identidad - Esto se deduce directamente de la definición de Peano. Cualquier cosa multiplicado por uno es en sí mismo.
- Inverse - Todos los números no nulos tienen una inverso multiplicativo.
Multiplicación también es una grupo abeliano, ya que sigue la propiedad conmutativa.
a × b = b × a
La multiplicación de diferentes tipos de números
Los números pueden contar (3 manzanas), orden (la tercera manzana), o medida (3,5 metros de altura); como la historia de las matemáticas ha pasado de contar con los dedos de la mecánica de modelado quantuum, multiplicación se ha generalizado a tipos más complicados y abstractos de los números, y para cosas que no son números (como matrices ) o que no se parecen mucho a los números (por ejemplo, cuaterniones).
- Los números enteros N × M es la suma de M copias de N cuando N y M son números enteros positivos. Esto le da el número de cosas en una matriz N de ancho y M alta. Generalización a números negativos se puede hacer por (N × -M) = - (N × M).
- Racionales Generalización a las fracciones A / B × C / D es multiplicando los numeradores y denominadores, respectivamente: A / B × C / D = (A × B) / (C x D). Esto le da al área de un rectángulo A / B alto y C / D de ancho, y es el mismo que el número de cosas en una matriz cuando los números racionales resultan ser números enteros.
- Reals x × y es el límite de los productos de los términos correspondientes en ciertas secuencias de números racionales que convergen para x e y, respectivamente, y es significativo en Cálculo . Esto le da al área de un rectángulo x amplia alta e y. Ver arriba .
- Complejos Teniendo en cuenta los números complejos Z1 y Z2 como pares ordenados o números reales (a1, b1) y (a2, b2), el producto z1 × Z2 es (a1 × a2 - b2 b1 ×, a1 a2 + b2 × × b1). Este es el mismo que para reales, a1 × a2, cuando las partes imaginarias b1 y b2 son cero.
- Otras generalizaciones Ver más arriba y Multiplicativa Group, que por ejemplo incluye la multiplicación de matrices. Una muy general y abstracto, el concepto de la multiplicación es como el (segundo) operación binaria "multiplicativamente denotado" en un anillo. Un ejemplo de un anillo que no es cualquiera de los sistemas de números anteriores es anillos de polinomios (se puede sumar y multiplicar polinomios, pero polinomios no son números en cualquier sentido usual.)
- División menudo división x / y es la misma que la multiplicación por un inverso, x × (1 / y). Multiplicación para algunos tipos de "números" puede tener la división correspondiente, sin inversas; en una Integral dominio x puede no tener inversa "1 / x", pero x / y se puede definir. En un Anillo de división no son inversas pero no son conmutativas (desde 1 / x X 1 / y no es lo mismo que 1 / y X 1 / x, x / y puede ser ambiguo).
