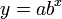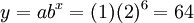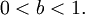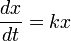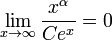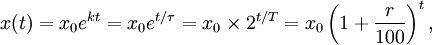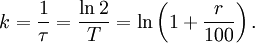Crescimento exponencial
Você sabia ...
Crianças SOS oferecem um download completo desta seleção para as escolas para uso em escolas intranets. Patrocinar crianças ajuda crianças no mundo em desenvolvimento para aprender também.
Em matemática , o crescimento exponencial (ou crescimento geométrico) ocorre quando a taxa de crescimento de uma função é sempre proporcional ao tamanho atual da função. Esse crescimento é referido a seguir uma lei exponencial; o modelo de crescimento exponencial simples é conhecido como o Modelo de crescimento malthusiano. Para qualquer quantidade em crescimento exponencial, quanto maior for a quantidade fica, mais rapidamente ele cresce. Uma alternativa é ditado 'A taxa de crescimento é proporcional ao estado de crescimento ". A relação entre o tamanho da variável dependente e sua taxa de crescimento é regido por uma lei estrita do tipo mais simples: proporção direta. Está provado no cálculo de que esta lei exige que a quantidade é dada pela função exponencial , se usarmos a escala de tempo correto. Isso explica o nome.
Fórmula básica
Se y cresce exponencialmente como uma função de x (x muitas vezes ser pensado como tempo), em seguida,
onde a é o valor inicial de Y, isto é, uma é que y é quando x = 0, e b é proporcional à taxa de crescimento inicial.
Exemplo: Se uma espécie de bactérias duplica a cada 10 minutos, começando com apenas uma bactéria, quantas bactérias estariam presentes após uma hora?
- Após intervalos de seis (6) 10 minutos, haveria 64 bactérias.
Isso também funciona com decaimento exponencial. Nesse caso, b é inferior a 1:
Intuição
O crescimento exponencial frase é frequentemente utilizado em contextos não-técnicos para significar crescimento meramente surpreendentemente rápido. Em um sentido estritamente matemático, porém, o crescimento exponencial tem um significado preciso e não significa necessariamente que o crescimento vai acontecer rapidamente. Na verdade, a população pode crescer exponencialmente, mas a um ritmo muito lento absoluta (como quando o dinheiro em um conta bancária ganha uma taxa de juros muito baixa, por exemplo), e pode crescer surpreendentemente rápido sem crescer exponencialmente. E algumas funções, como a função logística, o crescimento exponencial aproximada sobre apenas uma parte da sua gama. A seção "detalhes técnicos" abaixo explica exatamente o que é necessário para uma função para expor o verdadeiro crescimento exponencial.
Mas o princípio geral por trás do crescimento exponencial é que o maior um número fica, mais rápido ele cresce. Qualquer número exponencialmente crescente eventualmente crescer mais do que qualquer outro número que cresce a apenas uma taxa constante para a mesma quantidade de tempo (e também irá crescer mais do que qualquer função que cresce apenas subexponentially). Isso é demonstrado pelo enigma clássico em que uma criança é oferecido duas opções para uma crescente mesada semanal: a primeira opção começa em 1 cent e dobra a cada semana, enquanto a segunda opção começa em US $ 1 e aumenta em US $ 1 cada semana. Embora a segunda opção, crescendo a uma taxa constante de US $ 1 / semana, paga mais no curto prazo, a primeira opção, eventualmente, cresce muito maior:
| Semana | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Opção 1 | $ 0,01 | $ 0,02 | 0,04 dólares | $ 0,08 | $ 0,16 | 0,32 dólares | $ 0,64 | $ 1,28 | $ 2,56 | $ 5,12 | $ 10,24 | $ 20,48 | $ 40,96 | $ 81,92 | $ 163,84 | $ 327,68 | $ 655,36 | $ 1310,72 | $ 2621,44 |
| Opção 2 | $ 1 | Dois dólares | $ 3 | $ 4 | $ 5 | $ 6 | $ 7 | $ 8 | $ 9 | $ 10 | $ 11 | $ 12 | $ 13 | $ 14 | $ 15 | $ 16 | $ 17 | $ 18 | $ 19 |
Podemos descrever esses casos matematicamente. No primeiro caso, o subsídio na semana n é 2 n centavos; assim, na semana 15 o pagamento é de 2 15 = 32768 ¢ = $ 327,68. Todas as fórmulas da forma n k, onde k é um número imutável maior do que 1 (por exemplo, 2), e n é a quantidade de tempo decorrido, crescer exponencialmente. No segundo caso, o pagamento na semana n é simplesmente n + 1 dólares. O pagamento aumenta a uma taxa constante de $ 1 por semana.
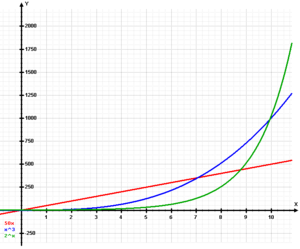
Esta imagem mostra um exemplo um pouco mais complicado de uma função exponencial ultrapassagem funções subexponencial:
A linha vermelha representa 50 x, semelhante à opção 2 no exemplo acima, exceto um aumento de 50 por semana em vez de 1. Seu valor é maior até que fica em torno de x 7. A linha azul representa o polinômio x 3. Polinômios crescer subexponentially, uma vez que o expoente (3 neste caso) permanece enquanto a base (x) mudanças constante. Esta função é maior do que os outros dois quando x é entre cerca de 7 e 9. Em seguida, a função exponencial 2 x (a verde) assume e torna-se maior do que as outras duas funções para todos os x maior do que cerca de 10.
Qualquer coisa que cresce na mesma percentagem a cada ano (ou a cada mês, dia, hora etc.) está a crescer exponencialmente. Por exemplo, se o número médio de descendentes de cada indivíduo (ou pares) de uma população permanece constante, a taxa de crescimento é proporcional ao número de indivíduos. Tal população em crescimento exponencial cresce três vezes mais rápido quando existem seis milhões de indivíduos como faz quando existem dois milhões. Contas bancárias com taxa fixa juros compostos crescer exponencialmente desde que não haja depósitos, retiradas ou taxas de serviço. Matematicamente, o saldo da conta bancária para uma conta começando com S dólares, ganhando uma taxa de juros anual r e deixado intocado por n anos pode ser calculado como 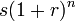 . Assim, em uma conta começando com US $ 1 e ganhar 5% ao ano, a conta terá
. Assim, em uma conta começando com US $ 1 e ganhar 5% ao ano, a conta terá 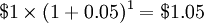 após 1 ano,
após 1 ano, 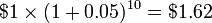 depois de 10 anos, e 131,50 dólares depois de 100 anos. Uma vez que o equilíbrio de partida e taxa não mudam, a quantidade
depois de 10 anos, e 131,50 dólares depois de 100 anos. Uma vez que o equilíbrio de partida e taxa não mudam, a quantidade 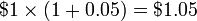 pode funcionar como o valor de k da fórmula dada anteriormente k n.
pode funcionar como o valor de k da fórmula dada anteriormente k n.
Detalhes técnicos
Seja x uma quantidade crescente exponencialmente em relação ao tempo t. Por definição, a taxa de variação dx / dt obedece à equação diferencial :
onde k ≠ 0 é a constante de proporcionalidade (relacionada com o número médio de descendentes por indivíduo, no caso da população). (Ver função logística para uma simples correção desse modelo de crescimento em que k não é constante). A solução para esta equação é a função exponencial 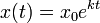 - Daí o nome crescimento exponencial ('e' ser um constante matemática). A constante
- Daí o nome crescimento exponencial ('e' ser um constante matemática). A constante 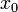 é o tamanho inicial da população.
é o tamanho inicial da população.
No longo prazo, o crescimento exponencial de qualquer tipo irá ultrapassar o crescimento linear de qualquer espécie (com base na Catástrofe Malthusiano), bem como qualquer polinomial de crescimento, ou seja, para todos α:
Há toda uma hierarquia de taxas de crescimento concebíveis que são mais lentos do que exponencial e mais rápido do que linear (no longo prazo). As taxas de crescimento pode também ser mais rápido do que exponencial. Os modelos lineares e exponenciais não são apenas simples, mas os candidatos são os de maior ocorrência na natureza.
Na equação diferencial acima, se k <0, então a quantidade experiências decaimento exponencial.
Quantidades de características de crescimento exponencial
A lei do crescimento exponencial pode ser escrito em formas diferentes, mas matematicamente equivalentes, usando um diferente de base . As formas mais comuns são os seguintes:
onde, como no exemplo acima, x 0 expressa a quantidade inicial (ou seja, x (t) para t = 0).
A quantidade k é chamada de constante de crescimento; a quantidade r é conhecida como a taxa de crescimento (por cento de aumento por unidade de tempo); 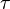 é o tempo e-dobrar; e T é a tempo de duplicação. Indicando uma destas quatro quantidades equivalentes automaticamente permite calcular os outros três, que estão ligadas através da seguinte equação (que podem ser derivados por tomado o logaritmo natural do acima):
é o tempo e-dobrar; e T é a tempo de duplicação. Indicando uma destas quatro quantidades equivalentes automaticamente permite calcular os outros três, que estão ligadas através da seguinte equação (que podem ser derivados por tomado o logaritmo natural do acima):
Um método aproximado popular para calcular o tempo de duplicação da taxa de crescimento é a Estado de 70, ou seja, 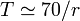 (Ou melhor:
(Ou melhor: 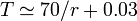 ).
).
Limitações dos modelos exponenciais
Um ponto importante sobre o crescimento exponencial é que, mesmo quando parece lento no curto prazo, torna-se impressionantemente rápido no longo prazo, com a quantidade inicial de duplicação no tempo de duplicação, em seguida, dobrando novamente e novamente. Por exemplo, uma taxa de crescimento populacional de 2% ao ano pode parecer pequena, mas realmente implica duplicação depois de 35 anos, dobrando novamente depois de mais 35 anos (ou seja, tornando-se 4 vezes a população inicial). Isto implica que tanto a quantidade observada, e o seu derivado de tempo será várias ordens de grandeza maior do que o que foi inicialmente concebido pela pessoa que concebeu o modelo de crescimento. Devido a isso, alguns efeitos não inicialmente tomadas em consideração vai distorcer a lei de crescimento, normalmente moderar-lo como, por exemplo, na lei logística. O crescimento exponencial de uma quantidade colocado no mundo real (ou seja, não no mundo da matemática abstrata) é um modelo válido para um período temporário de tempo somente.
Por esta razão, algumas pessoas (ver, por exemplo Limites do Crescimento) desafiar o modelo de crescimento exponencial no chão que é válido para o curto prazo somente, ou seja, nada pode crescer indefinidamente. Por exemplo, uma população em um ambiente fechado não pode continuar a crescer se ele come toda a comida e os recursos disponíveis; indústria não pode continuar bombeamento carbono do subsolo para a atmosfera para além dos limites relacionados com reservatórios de petróleo e as consequências da mudança climática . Existem problemas deste tipo para cada representação matemática do mundo real, mas são especialmente sentida para o crescimento exponencial, já que com esse crescimento acelera modelo como variáveis de aumentar em um feedback positivo, a um ponto em que o tempo de resposta humano para causar danos pode ser insuficiente. Sobre esses pontos, ver também as histórias exponenciais abaixo.
Exemplos de crescimento exponencial
- Biologia .
- Microorganismos em um prato de cultura vai crescer exponencialmente, em primeiro lugar, após a primeira microorganismo aparece (mas, em seguida, logisticamente até que a comida disponível está esgotado, quando o crescimento pára).
- Um vírus ( SARS, Nilo Ocidental, a varíola ) da infecciosidade suficiente (k> 0) vai se espalhar exponencialmente a princípio, se nenhum artificial imunização está disponível. Cada pessoa infectada pode infectar várias pessoas novas.
- A população humana , se o número de nascimentos e mortes por pessoa por ano deveriam permanecer nos níveis atuais (mas também ver o crescimento logística).
- Muitas respostas dos seres vivos para estímulos, incluindo humanos percepção, são logarítmicas respostas, que são o inverso das respostas exponenciais; o loudness e freqüência de som são percebidos de forma logarítmica, mesmo com muito tênue estímulo, dentro dos limites da percepção. Esta é a razão pela qual o crescimento exponencial brilho estímulos visuais é percebido pelos seres humanos como um aumento linear, em vez de um aumento exponencial. Isto tem valor de sobrevivência. Geralmente é importante para os organismos de responder a estímulos de uma ampla gama de níveis de níveis muito baixos, para níveis muito elevados, enquanto o precisão da avaliação de diferenças em níveis elevados de estímulo é muito menos importante para a sobrevivência.
- A tecnologia informática
- Poder dos computadores de processamento. Veja também a lei de Moore e singularidade tecnológica (em crescimento exponencial, não há singularidades. A singularidade aqui é uma metáfora.).
- Em teoria da complexidade computacional, algoritmos de computador de complexidade exponencial exigem uma quantidade exponencialmente crescente de recursos (por exemplo, tempo, memória do computador) para apenas um aumento constante em tamanho problema. Assim, por um algoritmo de complexidade de tempo 2 ^ x, se um problema de tamanho x = 10 requer 10 segundos para completar, e um problema de tamanho x = 11 requer 20 segundos, em seguida, um problema de tamanho x = 12 vai exigir 40 segundos. Este tipo de algoritmo normalmente torna-se inutilizável em tamanhos muito pequenos problemas, muitas vezes entre 30 e 100 itens (a maioria dos algoritmos de computador precisa ser capaz de resolver problemas muito maiores, até dezenas de milhares ou mesmo milhões de artigos em tempos razoáveis, algo que faria ser fisicamente impossível com um algoritmo exponencial). Além disso, os efeitos da Lei de Moore não ajudam a situação muito, porque dobrando a velocidade do processador apenas permite que você aumente o tamanho do problema por uma constante. Por exemplo, se um processador lento pode resolver problemas de tamanho x no tempo t, em seguida, um processador de duas vezes mais rápido poderia só resolver problemas de tamanho x + constantes, ao mesmo tempo t. Então exponencialmente algoritmos complexos são na maioria das vezes impraticável, ea busca de algoritmos mais eficientes é um dos objetivos centrais da ciência da computação.
- Crescimento do tráfego Internet .
- Investimento. O efeito de juros compostos ao longo de muitos anos tem um efeito substancial sobre a poupança e capacidade de uma pessoa se aposentar. Veja também Estado de 72
- Física
- Repartição avalanche num material dieléctrico. Um livre de elétrons torna-se suficientemente acelerados por um aplicado externamente campo elétrico que libera elétrons adicionais que colide com átomos ou moléculas do dielétrico. Estes elétrons secundários são acelerados também, a criação de um maior número de elétrons livres. O crescimento exponencial resultante de elétrons e íons podem rapidamente levar à completa falha dieléctrica do material.
- Reacção em cadeia nuclear (o conceito por trás armas nucleares ). Cada urânio núcleo que sofre fissão produz múltiplos neutrões , cada um dos quais pode ser absorvida por átomos de urânio adjacentes, fazendo com que, por sua vez fissão. Se a probabilidade de absorção de neutrões excede a probabilidade de fuga de neutrões (uma função do forma e massa do urânio), k> 0 e assim a taxa de produção de nêutrons e fissões de urânio induzidos aumenta exponencialmente, em uma reação descontrolada.
- Marketing multi-nível
- Aumentos exponenciais são prometeu aparecer em cada novo nível de linha descendente de um membro começando como cada membro posterior recruta mais pessoas.
Histórias exponenciais
As características surpreendentes de crescimento exponencial fascinam as pessoas através dos tempos.
Arroz em um tabuleiro de xadrez
Um cortesão apresentou o rei persa com um belo feito à mão tabuleiro de xadrez. O rei perguntou o que ele gostaria em troca de seu presente eo cortesão surpreendeu o rei pedindo um grão de arroz no primeiro quadrado, dois grãos no segundo, quatro grãos no terceiro etc. O rei prontamente concordou e pediu o arroz para ser trazido. Tudo correu bem no início, mas a exigência de 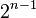 grãos no
grãos no 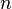 th quadrado exigiu mais de um milhão de grãos na praça 21, mais de um quatrilhão sobre o 41º e simplesmente não havia arroz suficiente no mundo inteiro para as praças finais. (De Meadows et al. 1972, p.29 via Porritt 2005)
th quadrado exigiu mais de um milhão de grãos na praça 21, mais de um quatrilhão sobre o 41º e simplesmente não havia arroz suficiente no mundo inteiro para as praças finais. (De Meadows et al. 1972, p.29 via Porritt 2005)
Para variação deste veja Segunda Metade do tabuleiro de xadrez em referência ao ponto onde um fator em crescimento exponencial começa a ter um impacto económico significativo na estratégia global de negócios de uma organização.
O lírio de água
Crianças francesas são contou uma história em que se imagine ter uma lagoa com lírio de água folhas flutuando na superfície. A população lírio dobra de tamanho a cada dia e, se não forem sufocar a lagoa em 30 dias, matando todos os outros seres vivos na água. Dia após dia, a planta parece pequena e por isso está decidido a deixá-lo a crescer até meia-cobre o lago, antes de cortá-lo de volta. Eles são, então, perguntou, em que dia que irá ocorrer. Isto é revelado para ser o dia 29, e em seguida, haverá apenas um dia para salvar a lagoa. (De Meadows et al. 1972, p.29 via Porritt 2005)