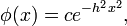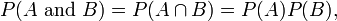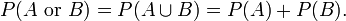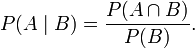Probabilidade

Probabilidade é a probabilidade ou chance de que algo é o caso ou vai acontecer. A teoria das probabilidades é amplamente utilizado em áreas como a estatística , matemática , ciência e filosofia para tirar conclusões sobre a probabilidade de eventos potenciais e os mecanismos subjacentes de sistemas complexos.

Interpretações

A palavra probabilidade não tem uma definição direta consistente. Na verdade, existem duas grandes categorias de interpretações de probabilidade: Frequentistas falar de probabilidades apenas quando lidar com bem definida experiências aleatórias. A frequência relativa de ocorrência dos resultados de uma experiência, quando se repete a experiência, é uma medida da probabilidade de que o evento aleatório. Bayesians, no entanto, atribuir probabilidades a qualquer declaração que seja, mesmo quando nenhum processo aleatório está envolvido, como uma forma de representar a sua plausibilidade subjetiva.

História

O estudo científico da probabilidade é um desenvolvimento moderno. Gambling mostra que tem havido um interesse em quantificar as idéias de probabilidade por milênios, mas as descrições matemáticas de uso nesses problemas só surgiu muito mais tarde.

De acordo com Richard Jeffrey, "Antes de meados do século XVII, o termo 'provável' (probabilis Latina) Aprovada significava, e foi aplicado nesse sentido, de maneira inequívoca, a opinião e para a ação. A ação provável ou opinião foi um como pessoas sensatas empreenderia ou detenham, nas circunstâncias. "

Com exceção de algumas considerações elementares feitas pela Girolamo Cardano no século 16, a doutrina das probabilidades datas para a correspondência de Pierre de Fermat e Blaise Pascal (1654). Christiaan Huygens (1657) deu a maior brevidade tratamento científico conhecido do assunto. Jakob Bernoulli de Ars Conjectandi (póstuma, 1713) e Abraham de Moivre de Doutrina da Chances (1718) tratou o assunto como um ramo da matemática. Ver Ian Hacking é O Surgimento de Probabilidade para uma história do início do desenvolvimento do próprio conceito de probabilidade matemática.

A teoria dos erros pode ser rastreada até De Roger Cotes Opera Miscellanea (póstuma, 1722), mas um livro de memórias preparadas por Thomas Simpson em 1755 (impresso em 1756) aplicada pela primeira vez a teoria à discussão de erros de observação. A reedição (1757) deste livro de memórias estabelece os axiomas que erros positivos e negativos são igualmente prováveis, e que há certos limites dentro dos quais atribuíveis todos os erros podem ser supostas para cair; erros contínuos são discutidos e uma curva de probabilidade é dada.

Pierre-Simon Laplace (1774) fez a primeira tentativa de deduzir uma regra para a combinação de observações dos princípios da teoria das probabilidades. Ele representou a lei da probabilidade de erros por uma curva 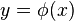, 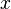sendo qualquer erro e 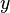sua probabilidade, e estabeleceu três propriedades dessa curva:

1. é simétrica como a 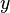-axis;
2. o 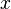é um -axis assíntota, a probabilidade de o erro sendo 0;
3. a área fechada é 1, sendo certo que existe um erro.

Deduziu uma fórmula para a média de três observações. Ele também deu (1781) uma fórmula para a lei da facilidade de erro (um termo devido a Lagrange, 1774), mas que levou a equações não gerenciáveis. Daniel Bernoulli (1778) introduziu o princípio do produto máxima das probabilidades de um sistema de erros simultâneos.

O método dos mínimos quadrados é devido Adrien-Marie Legendre (1805), que introduziu em seus Nouvelles méthodes pour la détermination des orbites des Cometes (Novos métodos para determinar as órbitas de cometas). Em ignorância da contribuição de Legendre, um escritor irlandês-americano, Robert Adrain, editor de "The Analyst" (1808), primeiro deduziu a lei da facilidade de erro,

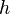sendo uma constante que depende da precisão da observação, e um factor de escala garantindo que a área sob a curva é igual a 1. Ele deu duas provas, o segundo sendo essencialmente o mesmo que John Herschel (1850). Gauss deu a primeira prova de que parece ter sido conhecido na Europa (o terceiro depois de Adrain) em 1809. Outras provas foram dadas por Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), WF Donkin (1844, 1856), e Morgan Crofton (1870). Outros contribuintes foram Ellis (1844), De Morgan (1864), Glaisher (1872), e Giovanni Schiaparelli (1875). (1856) A fórmula de Peters para , A probabilidade de erro de uma única observação, é bem conhecido.

No século XIX, os autores sobre a teoria geral incluído Laplace , Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion, e Karl Pearson. Augustus De Morgan e George Boole melhoraram a exposição da teoria.

No lado geométrico (veja geometria) contribuidores para integrais Os tempos educativos foram influentes (Miller, Crofton, McColl, Wolstenholme, Watson, e Artemas Martin).

Tratamento matemático

Em matemática uma probabilidade de um caso, A é representado por um número real na gama de 0 a 1 e escrito como P (A), P (a) ou Pr (A). Um evento impossível tem uma probabilidade de 0, e um determinado evento tem uma probabilidade de 1. No entanto, as converses nem sempre são verdadeiras: probabilidade 0 eventos nem sempre são impossíveis, nem de probabilidade 1 certos. A distinção bastante sutil entre "certo" e "probabilidade 1" é tratado com maior profundidade no artigo sobre " quase certamente ".

O oposto ou do complemento de um evento é um evento [não A] (isto é, o caso de não ocorrendo); a sua probabilidade é dada pela

. Como exemplo, a chance de não rolar um seis em um dado de seis lados é

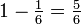= . Ver Evento complementar para um tratamento mais completo.

Se dois eventos, A e B são independente, em seguida, o probabilidade conjunta é

por exemplo, se duas moedas são viradas a chance de ambas as cabeças sendo é .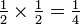

Se dois eventos são mutuamente exclusivos, em seguida, a probabilidade de ocorrência é de

Por exemplo, a chance de rolar um 1 ou 2 em um dado de seis lados é .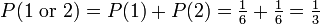

Se os eventos não são mutuamente exclusivos, em seguida,

.

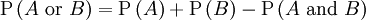Probabilidade condicional é a probabilidade de algum evento A, dada a ocorrência de algum outro evento B. Probabilidade condicional é escrita P (A | B), e é lido "a probabilidade de A, dado B". É definido pela

Se 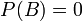em seguida 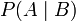é indefinido.

Resumo das probabilidades

Evento	Probabilidade
A
Um não
A ou B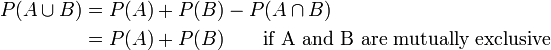
A e B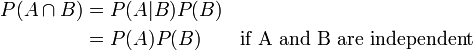
A dado B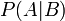

Teoria

À semelhança de outros teorias, a teoria das probabilidades é uma representação dos conceitos probabilísticos em termos formais, isto é, em termos que podem ser considerados separadamente de seus significados. Esses termos formais são manipulados pelas regras da matemática e da lógica, e quaisquer resultados são então interpretados ou traduzidos de volta para o domínio do problema.

Houve pelo menos duas tentativas bem-sucedidas para formalizar a probabilidade, ou seja, o Formulação de Kolmogorov eo Formulação de Cox. Na formulação de Kolmogorov (ver espaço de probabilidade ), conjuntos são interpretados como eventos e em si como uma probabilidade medir em uma classe de conjuntos. Em Teorema, a probabilidade de Cox é tomado como um primitivo (isto é, não ainda analisados) ea ênfase está na construção de uma atribuição consistente de valores de probabilidade a proposições. Em ambos os casos, o leis da probabilidade são os mesmos, com exceção de detalhes técnicos.

Há outros métodos para a quantificação de incerteza, como o Teoria Dempster-Shafer e teoria de possibilidades, mas aqueles que são essencialmente diferentes e não é compatível com as leis da probabilidade como eles são geralmente entendida.

Aplicações

Dois principais aplicações da teoria da probabilidade na vida cotidiana estão em avaliação de riscos e no comércio em mercados de commodities. Os governos normalmente aplicar métodos probabilísticos em regulação ambiental onde é chamada de " análise de caminho ", muitas vezes medição do bem-estar usando métodos que sejam de natureza estocástica, e escolhendo projetos para empreender com base em análises estatísticas de seu provável efeito sobre a população como um todo. Não é correto dizer que as estatísticas estão envolvidas na modelagem em si, como normalmente as avaliações da risco são de uma só vez e, portanto, requerem modelos mais fundamentais de probabilidade, por exemplo, "a probabilidade de outro 9/11". A lei de números pequenos tende a se aplicar a todas as opções e percepção do efeito de tais escolhas, o que torna as medidas de probabilidade uma questão política.

Um bom exemplo é o efeito da probabilidade percebida de qualquer conflito no Oriente Médio generalizada sobre os preços do petróleo - que têm efeitos em cascata na economia como um todo. Uma avaliação por um trader de commodities que uma guerra é mais provável vs. menos provável envia os preços para cima ou para baixo, e sinais de outros comerciantes do referido parecer. Assim, as probabilidades não são avaliados de forma independente nem necessariamente muito racionalmente. A teoria de finanças comportamentais surgiu para descrever o efeito de tal groupthink sobre preços, sobre a política e sobre a paz e conflito.

É razoável dizer-se que a descoberta de métodos rigorosos para avaliar e combinar avaliações de probabilidade teve um efeito profundo sobre a sociedade moderna. Assim, pode ser de alguma importância para a maioria dos cidadãos a compreender como as probabilidades e avaliações de probabilidade são feitas, e como elas contribuem para reputações e decisões, especialmente em uma democracia .

Outra aplicação importante da teoria da probabilidade na vida cotidiana é confiabilidade. Muitos produtos de consumo, tais como automóveis e produtos eletrônicos de consumo, utilizar teoria fiabilidade na concepção do produto, a fim de reduzir a probabilidade de falha. A probabilidade de falha está também intimamente associados com o produto de garantia.

Relação à aleatoriedade

Em um universo determinista, com base em newtonianos conceitos, não há nenhuma probabilidade se todas as condições são conhecidos. No caso de uma roda de roleta, se a força da mão e do período de força que são conhecidos, em seguida, o número no qual a bola irá parar seria uma certeza. Naturalmente, isto também pressupõe o conhecimento de inércia e de atrito da roda, peso, suavidade e arredondamento da bola, as variações na velocidade da mão durante a viragem e assim por diante. A descrição probabilística pode, assim, ser mais útil do que a mecânica newtoniana para analisar o padrão de resultados de repetidos rolos de roleta. Os físicos enfrentam a mesma situação em teoria cinética dos gases, em que o sistema, enquanto, em princípio, determinista, é tão complexa (com o número de moléculas, tipicamente da ordem de grandeza da constante de Avogadro ( 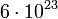) Que só descrição estatística de suas propriedades é viável.

Uma descoberta revolucionária da física do século 20 foi o caráter aleatório de todos os processos físicos que ocorrem em escalas microscópicas e são regidos pelas leis da mecânica quântica . O própria função de onda evolui de forma determinística, desde que nenhuma observação é feita, mas, de acordo com a prevalecente Interpretação de Copenhague, a aleatoriedade provocada pelo função de onda em colapso quando uma observação é feita, é fundamental. Isto significa que a teoria das probabilidades é necessária para descrever a natureza. Outros nunca chegou a um acordo com a perda de determinismo. Albert Einstein famosa comentou em uma carta ao Max Born: überzeugt Jedenfalls bin ich, dass der Alte nicht würfelt (Estou convencido de que Deus não joga dados).. Embora existam pontos de vista alternativos, tais como a de decoerência quântica sendo a causa de um colapso aparente aleatória, não existe actualmente um consenso firme entre os físicos que a teoria da probabilidade é necessário descrever fenômenos quânticos.

Cotações

• Damon Runyon, "Pode ser que a raça nem sempre é dos ligeiros, nem a batalha para o forte - mas essa é a maneira de apostar."
• Pierre-Simon Laplace "É notável que uma ciência que começou com a consideração de jogos de azar deveria ter se tornado o mais importante objeto do conhecimento humano." Teoria Analítica des Probabilités de 1812.
• Richard von Mises "A extensão ilimitada da validade das ciências exatas era uma característica do racionalismo exagerado do século XVIII" (em referência a Laplace). Probabilidade, Estatística, e Verdade, p 9. edição Dover, 1981 (republicação da segunda edição Inglês, 1957).