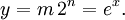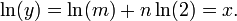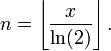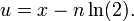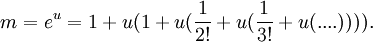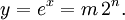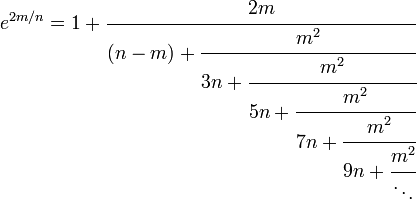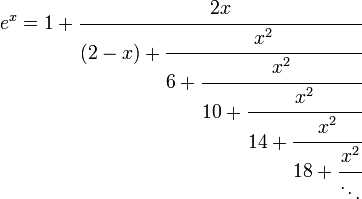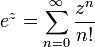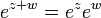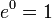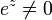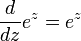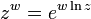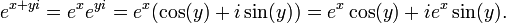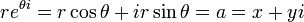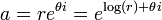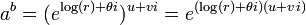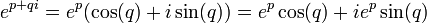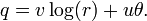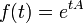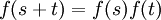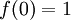Função exponencial
Você sabia ...
Esta seleção Wikipedia está offline disponível a partir de Crianças SOS, para distribuição no mundo em desenvolvimento. Patrocinar crianças ajuda crianças no mundo em desenvolvimento para aprender também.
A função exponencial é uma função em matemática . A aplicação desta função de um valor x é escrito como exp (X). De forma equivalente, isto pode ser escrito sob a forma e X, em que E é uma constante matemática, o base do logaritmo natural, o que equivale a aproximadamente 2,718281828, e também é conhecido como Euler número 's.

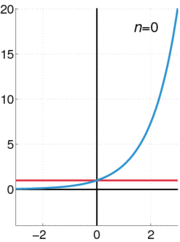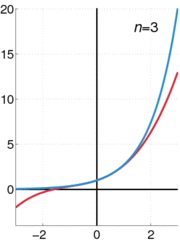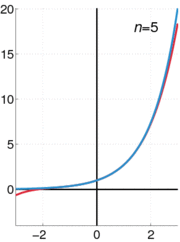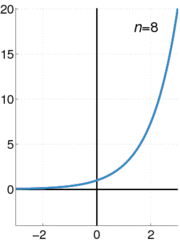
Como uma função das reais variáveis X, o gráfico de y = e x é sempre positivo (acima do eixo x) e a aumentar (visto da esquerda para a direita). Ele nunca toca o eixo x, embora se aproxima arbitrariamente a ele (assim, o eixo x é um horizontal asymptote para o gráfico). A sua função inversa , o logaritmo natural , ln (x), é definida para todo x positivo. A função exponencial é ocasionalmente referido como o anti-logaritmo . No entanto, esta terminologia parece ter caído em desuso nos últimos tempos.
Às vezes, especialmente nas ciências , o termo função exponencial é mais geralmente usado para funções de forma a x Ka, em que um, chamada a base, é qualquer número real positivo não é igual a um. Este artigo irá focar inicialmente a função exponencial com base e, o número de Euler.
Em geral, o variável x pode ser qualquer real ou número complexo , ou mesmo um tipo totalmente diferente de objeto matemático; veja a definição formal abaixo .
Propriedades
Mais simplesmente, funções exponenciais multiplicar a uma taxa constante. Por exemplo, a população de uma cultura bacteriana que duplica a cada 20 minutos pode (approximatively, como este não é realmente um problema contínuo) ser expressa como um exponencial, assim como o valor de um veículo que diminui em 10% por ano.
Usando o logaritmo natural, pode-se definir funções exponenciais mais gerais. A função
definida para todo a> 0, e todos os números reais x, é chamado a função exponencial com base de um. Note-se que esta definição de 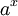 baseia-se na existência previamente estabelecida da função
baseia-se na existência previamente estabelecida da função 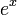 , Definida para todos os números reais. (Aqui, nós nem formalmente nem conceitualmente esclarecer se essa função existe ou o que expoentes não naturais são supostamente para dizer.)
, Definida para todos os números reais. (Aqui, nós nem formalmente nem conceitualmente esclarecer se essa função existe ou o que expoentes não naturais são supostamente para dizer.)
Note-se que a equação acima é válido para A = E, desde
Funções exponenciais "traduzir entre adição e multiplicação", como está expresso nos três primeiros e quinto das seguintes leis exponenciais:
Estes são válidos para todos os números reais um positivo e b e tudo real números x e y. Expressões envolvendo frações e raízes muitas vezes pode ser simplificada usando a notação exponencial:
e, para qualquer um> 0, b número real, e o inteiro n> 1:
Derivados e equações diferenciais
A importância das funções exponenciais em matemática e as ciências resulta principalmente de propriedade de seus derivados . Em particular,
Isto é, e x é o seu próprio derivado . Funções da forma  para constante K são as únicas funções com essa propriedade. (Isso decorre do Picard-Lindelöf teorema, com
para constante K são as únicas funções com essa propriedade. (Isso decorre do Picard-Lindelöf teorema, com  e
e 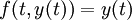 .) Outras formas de dizer a mesma coisa incluem:
.) Outras formas de dizer a mesma coisa incluem:
- A inclinação do gráfico em qualquer ponto é a altura da função nesse ponto.
- A taxa de aumento da função em que x é igual ao valor da função em x.
- A função resolve o equação diferencial
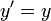 .
. - exp é um ponto fixo de derivados como funcional
Na verdade, várias equações diferenciais dar origem a funções exponenciais, incluindo o Equação de Schrödinger ea A equação de Laplace, bem como para as equações movimento harmônico simples.
Para funções exponenciais com outras bases:
Assim, qualquer função exponencial é um múltiplo constante do seu próprio derivado.
Se a taxa de crescimento ou decadência de uma variável é proporcional ao seu tamanho - como é o caso no crescimento populacional ilimitada (ver Catástrofe malthusiana), compostos continuamente interesse, ou decaimento radioativo - em seguida, a variável pode ser escrito como uma constante vezes uma função exponencial de tempo.
Além disso, para qualquer função diferenciável f (x), encontramos, pela regra da cadeia:
Definição formal
A função exponencial e x pode ser definida em uma variedade de formas equivalentes, como um série infinita. Em particular, pode ser definido por uma série de potência :
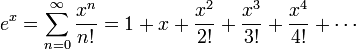 .
.
Note-se que esta definição, tem a forma de uma série de Taylor . Usando uma definição alternativa para a função exponencial deverá conduzir ao mesmo resultado quando expandida como uma série de Taylor .
Uma definição menos comum define  como a solução de
como a solução de 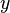 com a equação
com a equação
Valor numérico
Para obter o valor numérico da função exponencial, a série infinita pode ser reescrita como:
Esta expressão irão convergir rapidamente se podemos assegurar que x é inferior a um.
Para garantir isso, podemos usar a seguinte identidade.
- Onde
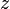 é a parte inteira
é a parte inteira 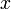
- Onde
 é a parte fracionária
é a parte fracionária 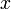
- Assim,
 é sempre menor do que 1 e
é sempre menor do que 1 e  e
e 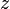 adicionar até
adicionar até 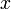 .
.
O valor da constante de e Z pode ser calculado multiplicando-se de antemão e com a própria vezes z.
Computação de exp (x) para o real x
Um algoritmo de melhor ainda podem ser encontrados como se segue.
Primeiro, observe que a resposta y = x e é geralmente um número de ponto flutuante representada por um mantissa e um expoente m n então y = m 2 n para algum inteiro n e adequadamente pequena m. Assim, temos:
Tomando log em ambos os lados das duas últimas nos dá:
Deste modo, obtemos n como o resultado da divisão por X log (2) e encontrar o maior inteiro que não é maior do que este - isto é, o função do assoalho:
Tendo encontrado n podemos então encontrar a parte fracionária u como este:
O número u é pequena e no intervalo de 0 ≤ u <ln (2) e por isso, pode utilizar a série anteriormente mencionado para calcular m:
Tendo encontrado m e n então podemos produzir y simplesmente combinando os dois em um número de ponto flutuante:
Frações contínuas para e x
Via identidade de Euler:
Técnicas mais avançadas são necessárias para construir a seguinte:
Definir m = x e N = 2 rendimentos
Computação de  por número natural (número inteiro positivo) n
por número natural (número inteiro positivo) n
Existe uma maneira rápida de calcular  quando o símbolo n representa um número inteiro positivo. Ele faz uso do facto de que o teste é um número impar tal é muito fácil para um computador e dividindo por 2 também é rápido, simplesmente deslocando todos os bits para a direita.
quando o símbolo n representa um número inteiro positivo. Ele faz uso do facto de que o teste é um número impar tal é muito fácil para um computador e dividindo por 2 também é rápido, simplesmente deslocando todos os bits para a direita.
passo 1, inicializar algumas variáveis
y: = 1, k: = n, F: = a
etapa 2, teste k
se k é 0, vá para a etapa 7
passo 3, (k não é 0 aqui, teste se k é mesmo)
se k é mesmo ir para a etapa 5
passo 4, (k é estranho aqui, multiplicar in) 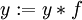
etapa 5, (dividir por 2 k / ignore restante, divida por turno, também quadrada f)
k: k = deslocamento para a direita por 1 f: = f * f
passo 6, (circular)
volte para o passo 2
etapa 7, (feito, y é um resultado = n)
retornar y
Em C , você pode escrever o algoritmo parecido com isto:
poder de casal (duplo um, sem assinatura int n) {double y = 1; double f = a; unsigned int k = n; while (k = 0!) {if ((k & 1) = 0!) y = f *; k >> = 1; f * = f; } Retornar y; }poder de casal (duplo um, sem assinatura int n) {double y = 1; double f = a; unsigned int k = n; while (k = 0!) {if ((k & 1) = 0!) y = f *; k >> = 1; f * = f; } Retornar y; }
Enquanto uma multiplicação ingênuo de um ^ 100 exigiria 100 iterações de um loop de multiplicação de um loop for, esta apenas 7 vezes (O número 100 é escrito usando 7 bits).
Este algoritmo pode ser facilmente estendido para inteiros assinados por fazer as seguintes etapas antes e depois:
passo 1. Se k é negativo, nega o valor assim que nós começamos um k positivo. n ainda se lembra do valor original.
passo 2. Execute o cálculo acima para 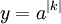
passo 3. Se n for negativo, inverter o resultado até y: = 1 / y. y é agora o resultado de  para um número inteiro n.
para um número inteiro n.
No plano complexo
Tal como no verdadeiro caso, a função exponencial pode ser definida no plano complexo , em várias formas equivalentes. Algumas dessas definições espelhar as fórmulas para a função exponencial de valor real. Especificamente, ainda se pode usar a definição de série de potência, onde o valor real é substituído por um complexo:
Usando esta definição, é fácil mostrar por que  detém no plano complexo.
detém no plano complexo.
Outra definição estende a verdadeira função exponencial. Primeiro, afirmamos a propriedade desejada 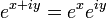 . Para
. Para  usamos a verdadeira função exponencial. Em seguida, proceder através da definição apenas:
usamos a verdadeira função exponencial. Em seguida, proceder através da definição apenas: 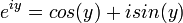 . Assim, usamos a verdadeira definição, em vez de ignorá-lo.
. Assim, usamos a verdadeira definição, em vez de ignorá-lo.
Quando considerado como uma função definida no plano complexo , a função exponencial retém as propriedades importantes
para todo z e w.
É um função holomorfa que é periódica com período imaginário 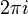 e pode ser escrita como
e pode ser escrita como
em que a e b são valores reais. Esta fórmula conecta a função exponencial com as funções trigonométricas e para o funções hiperbólicas. Assim, vemos que tudo funções elementares, exceto para os polinômios brotar da função exponencial, de uma forma ou de outra.
Veja também A fórmula de Euler.
Estendendo o logaritmo natural de argumentos complexos produz um função multi-valorizados, ln (z). Podemos, então, definir uma exponenciação mais geral:
para todos os números complexos z e w. Esta é também uma função multi-valorizados. As leis exponenciais acima enunciados permanecer fiel se interpretado corretamente como declarações sobre funções com valores múltiplos.
A função exponencial mapeia qualquer linha no plano complexo de uma espiral logarítmica no plano complexo com o centro no origem. Dois casos especiais pode ser observado: quando a linha original é paralelo ao eixo real, o sprial resultante nunca se fecha sobre si mesma; quando a linha original é paralelo ao eixo imaginário, a espiral resultante é um círculo de raio alguns.
- A representação gráfica da função exponencial no plano complexo
Computação de exp (z) para um complexo z
Este é bastante simples, dada a fórmula
Observe que o argumento y para as funções trigonométricas é real.
Computação de  em que tanto a como b são complexos
em que tanto a como b são complexos
Isto também é simples, dadas as fórmulas:
se a = x + Yi e b = u + VI que pode converter um primeiro para coordenadas polares por encontrar um 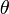 e um
e um  de tal modo que:
de tal modo que:
ou
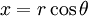 e
e 
Assim,  ou
ou 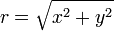 e
e 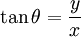 ou
ou 
Agora, temos que:
assim:
O expoente é, assim, um simples multiplicação dos dois valores complexos que produzam um resultado complexo que pode então ser trazido de volta para o formato cartesiano regular pela fórmula:
em que p é a parte real da multiplicação:
e q é a parte imaginária da multiplicação:
Note-se que todos 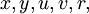
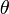 ,
,  e
e 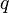 são todos os valores reais nestes cálculos. O resultado
são todos os valores reais nestes cálculos. O resultado  é assim
é assim 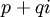 .
.
Observe também que uma vez que calcular e uso 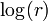 ao invés de si r você não tem que calcular a raiz quadrada. Em vez disso simplesmente calcular
ao invés de si r você não tem que calcular a raiz quadrada. Em vez disso simplesmente calcular 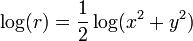 . Atente para potencial estouro embora e, possivelmente, reduza o x e y antes de computação
. Atente para potencial estouro embora e, possivelmente, reduza o x e y antes de computação 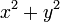 por um poder adequado, de 2 de se
por um poder adequado, de 2 de se 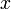 e
e 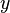 são tão grandes que você iria transbordar. Se você não corre o risco de estouro negativo, ampliar por um poder adequado de 2 antes de calcular a soma dos quadrados. Em ambos os casos você, em seguida, obter a versão em escala de
são tão grandes que você iria transbordar. Se você não corre o risco de estouro negativo, ampliar por um poder adequado de 2 antes de calcular a soma dos quadrados. Em ambos os casos você, em seguida, obter a versão em escala de 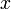 - Podemos chamá-lo
- Podemos chamá-lo  ea versão em escala de
ea versão em escala de 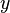 - Chame-
- Chame- 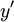 e assim que você começa:
e assim que você começa:
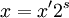 e
e 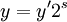
onde  é o fator de escala.
é o fator de escala.
Então você começa 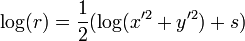 onde
onde  e
e 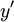 são dimensionadas de modo que a soma dos quadrados não vai transbordar ou underflow. Se
são dimensionadas de modo que a soma dos quadrados não vai transbordar ou underflow. Se 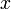 é muito grande, enquanto
é muito grande, enquanto 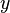 é muito pequeno para que você não pode encontrar um tal fator de escala que você vai transbordar de qualquer maneira e assim a soma é essencialmente igual
é muito pequeno para que você não pode encontrar um tal fator de escala que você vai transbordar de qualquer maneira e assim a soma é essencialmente igual 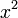 desde y é ignorada e, assim que você começa
desde y é ignorada e, assim que você começa 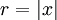 neste caso, e
neste caso, e 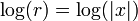 . O mesmo acontece no caso quando
. O mesmo acontece no caso quando 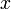 é muito pequena e
é muito pequena e 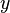 é muito grande. Se ambos são muito grandes ou ambos são muito pequenas pode encontrar um fator de escala, como mencionado anteriormente.
é muito grande. Se ambos são muito grandes ou ambos são muito pequenas pode encontrar um fator de escala, como mencionado anteriormente.
Note-se que esta função é, em geral, multivalued para argumentos complexos. Isto é porque a rotação de um único ponto através de qualquer ângulo, mais de 360 graus, ou  radianos, é o mesmo que o ângulo de rotação através de si. Assim
radianos, é o mesmo que o ângulo de rotação através de si. Assim 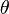 acima não é único:
acima não é único: 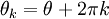 para qualquer número inteiro
para qualquer número inteiro  faria bem. A convenção, porém, é que, quando
faria bem. A convenção, porém, é que, quando 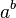 é tomado como um valor único, deve ser porque para
é tomado como um valor único, deve ser porque para  , Ou seja. usamos o menor valor possível (em valor absoluto) de teta, que tem uma magnitude de, no máximo,
, Ou seja. usamos o menor valor possível (em valor absoluto) de teta, que tem uma magnitude de, no máximo, 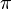 .
.
Matrizes e álgebras de Banach
A definição da função exponencial dada acima pode ser utilizado para todos os textualmente Banach álgebra, e em particular para quadrados matrizes (caso em que a função é chamada a matriz exponencial). Neste caso, temos
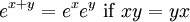

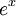 é invertível com inversa
é invertível com inversa 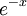
- o derivado de
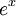 no ponto
no ponto 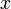 é que o mapa linear que envia
é que o mapa linear que envia 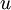 para
para 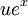 .
.
No contexto da álgebra de Banach não comutativos, tais como álgebra de matrizes ou operadores Banach ou Espaços de Hilbert, a função exponencial é muitas vezes considerado como uma função de um argumento real:
onde A é um elemento fixo da álgebra e t é um número real. Esta função tem as propriedades importantes
Em álgebras de Lie
O o envio de um mapa exponencial Deite álgebra ao Grupo de Lie que deu origem a ele compartilha as propriedades acima, o que explica a terminologia. Na verdade, uma vez que R é a álgebra de Lie do grupo de Lie de todos os números reais positivos com a multiplicação, a função exponencial ordinário para argumentos reais é um caso especial da situação álgebra de Lie. Da mesma forma, uma vez que a álgebra de Lie M (n, R) de todas as matrizes reais quadrados pertence ao grupo de Lie de todas as matrizes quadradas invertíveis, a função exponencial para matrizes quadradas é um caso especial do mapa exponencial álgebra de Lie.
Função exponencial dupla
A função exponencial dupla prazo pode ter dois significados:
- uma função com dois termos exponenciais, com diferentes expoentes
- uma função
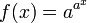 ; esta cresce ainda mais rápido do que uma função exponencial; por exemplo, se a = 10: f (-1) = 1,26, F (0) = 10, F (1) = 10 10, f (2) = 10 100 = gugol, ..., F (100) = googolplex.
; esta cresce ainda mais rápido do que uma função exponencial; por exemplo, se a = 10: f (-1) = 1,26, F (0) = 10, F (1) = 10 10, f (2) = 10 100 = gugol, ..., F (100) = googolplex.
Fatoriais crescer mais rápido do que funções exponenciais, mas mais lento do que as funções duplamente exponencial. Números de Fermat, gerados por 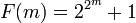 e números Mersenne duplos gerados pela
e números Mersenne duplos gerados pela 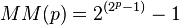 são exemplos de funções exponenciais duplos.
são exemplos de funções exponenciais duplos.
Imóveis similares de  e a função
e a função 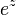
A função 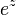 não é em C (Z) (ou seja. não o quociente de dois polinómios com coeficientes complexos).
não é em C (Z) (ou seja. não o quociente de dois polinómios com coeficientes complexos).
Para números complexos n distintas 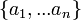 ,
,  é linearmente independente sobre C (Z).
é linearmente independente sobre C (Z).
A função 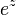 é transcendental sobre C (z).
é transcendental sobre C (z).
Periodicidade
Para todos os números inteiros n e complexo x:
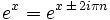
Prova:
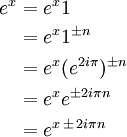
Para todos os inteiros positivos n e um complexo & x:
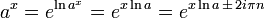
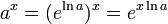
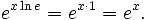
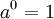
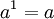

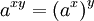
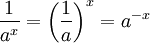

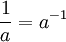
![\, \ Sqrt [n] {a ^ b} = \ left (\ sqrt [n] {a} \ right) ^ b = a ^ {b / n}.](../../images/90/9057.png)
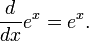
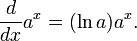
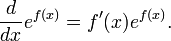

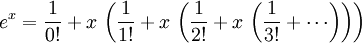
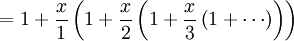

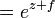
![\, = E ^ z \ times \ left [{1 \ over 0!} + F \, \ left ({1 \ over 1!} + F \, \ left ({1 \ over 2!} + F \, \ left ({1 \ over 3!} + \ cdots \ right) \ right) \ right) \ right]](../../images/90/9079.png)