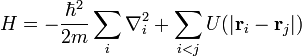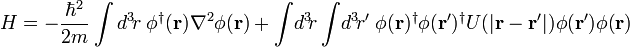Théorie quantique des champs
Contexte des écoles Wikipédia
SOS Enfants a fait cette sélection Wikipedia aux côtés d'autres écoles des ressources . Visitez le site Web d'enfants SOS au http://www.soschildren.org/
| Théorie quantique des champs |
|---|
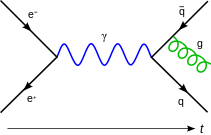 Diagramme de Feynman |
| Histoire |
Fond
|
Symétries
|
Outils
|
Équations
|
|
Théories incomplètes
|
Les scientifiques
|
La théorie quantique des champs (QFT) est un cadre théorique pour la construction mécanique quantique modèles de terrain comme les systèmes ou, de façon équivalente, des systèmes à plusieurs corps. Il est largement utilisé dans la physique des particules et de la physique de la matière condensée . La plupart des théories en physique des particules moderne, y compris le modèle standard des particules élémentaires et leurs interactions, sont formulées comme relativistes théories quantiques des champs. En matière condensée, théories de champ quantiques sont utilisés dans de nombreuses circonstances, notamment celles où le nombre de particules est autorisé à varier, par exemple, dans le La théorie BCS de la supraconductivité .
Histoire
Théorie quantique des champs origine dans le 1920 du problème de la création d'une théorie quantique de la champ électromagnétique. En 1926 , Max Born, Pascual Jordanie et Werner Heisenberg construit une telle théorie en exprimant le domaine de interne degrés de liberté comme un ensemble infini de oscillateurs harmoniques et en utilisant la procédure habituelle pour quantifier ces oscillateurs ( quantification canonique). Cette théorie suppose qu'aucune accusation ou courants électriques étaient présents et qu'on appellerait aujourd'hui un la théorie en champ libre. La première théorie assez complète électrodynamique quantique, qui comprenait à la fois le champ électromagnétique et chargées électriquement la matière (en particulier, électrons ) comme des objets de la mécanique quantique, a été créé par Paul Dirac en 1927 . Cette théorie quantique des champs pourrait être utilisé pour modéliser les processus importants tels que l'émission d'un photon par un électron tomber dans un état quantique d'énergie inférieure, un processus dans lequel le nombre de particules change - un atome à l'état initial devient un atome plus un photon dans l'état final. Il est désormais entendu que la capacité de décrire ces processus est l'un des aspects les plus importants de la théorie quantique des champs.
Il était évident dès le début que un traitement quantique correcte du champ électromagnétique devait intégrer en quelque sorte d'Einstein relativité la théorie, qui avait après tout développé à partir de l'étude des électromagnétisme classique. Cette nécessité de mettre sur pied la relativité et la mécanique quantique était la deuxième motivation majeure dans le développement de la théorie quantique des champs. Pascual Jordanie et Wolfgang Pauli a montré dans 1928 que les champs quantiques pourraient être apportées à se comporter de la façon prédite par la relativité restreinte cours transformations de coordonnées (en particulier, ils ont montré que le domaine commutateurs étaient Lorentz invariant), et 1933 Niels Bohr et Leon Rosenfeld a montré que ce résultat pourrait être interprété comme une limitation de la capacité à mesurer les champs au séparations comme l'espace, exactement comme requis par la relativité. Un nouvel élan pour la théorie quantique des champs est venu avec la découverte de la Équation de Dirac, une équation simple particules obéissant à la fois la relativité et la mécanique quantique, quand il a été démontré que plusieurs de ses propriétés indésirables (tels que les états à énergie négative) pourrait être éliminé en reformulant l'équation de Dirac comme une théorie quantique des champs. Ce travail a été effectué par Wendell Furry, Robert Oppenheimer , Vladimir Fock, et d'autres.
Le troisième fil dans le développement de la théorie quantique des champs était la nécessité de manipuler les statistiques de systèmes à plusieurs particules constamment et avec facilité. En 1927 , la Jordanie a essayé de prolonger la quantification canonique de champs aux fonctions d'onde à plusieurs corps de des particules identiques, une procédure qui est parfois appelé seconde quantification. En 1928 , la Jordanie et Eugene Wigner a constaté que le champ quantique décrivant électrons, ou autre fermions, devaient être élargi à l'aide anti-navette opérateurs de création et d'annihilation en raison de la Principe d'exclusion de Pauli. Ce fil du développement a été incorporé dans la théorie à plusieurs corps, et fortement influencées physique de la matière condensée et la physique nucléaire .
Malgré ses premiers succès, la théorie quantique des champs a été en proie à plusieurs difficultés théoriques graves. Beaucoup de grandeurs physiques apparemment inoffensifs, tels-que le changement d'énergie d'états électroniques dus à la présence du champ électromagnétique, ont donné l'infini - un résultat absurde - lorsqu'ils sont calculés en utilisant la théorie quantique des champs. Ce «problème de divergence" a été résolu au cours de la Années 1940 par Bethe, Tomonaga, Schwinger, Feynman , et Dyson, à travers la procédure dite de renormalisation . Cette phase de développement a culminé avec la construction de la théorie moderne de électrodynamique quantique (QED). À partir de la 1950 avec les travaux de Yang et Mills, QED a été généralisé à une classe de théories quantiques des champs appelés théorie de jauge. Le 1960 et 1970 a vu la formulation d'une théorie de jauge maintenant connu comme le modèle standard de la physique des particules , qui décrit toutes les particules élémentaires connues et les interactions entre eux. Le faible partie de l'interaction du modèle standard a été formulée par Sheldon Glashow, avec le Mécanisme de Higgs ajoutée par Steven Weinberg et Abdus Salam. La théorie est révélé être conforme par Gerardus 't Hooft et Martinus Veltman.
Également au cours de la 1970, les développements parallèles dans l'étude de transitions de phase dans la matière condensée conduit Leo Kadanoff, Michael Fisher et Kenneth Wilson (l'extension du travail de Ernst Stueckelberg, Andre Peterman, Murray Gell-Mann et Francis Low) à un ensemble d'idées et de méthodes connu sous le nom groupe de renormalisation. En fournissant une meilleure compréhension de la physique de la procédure de renormalisation inventé dans le 1940, le groupe de renormalisation déclenché ce qu'on a appelé la «grande synthèse" de la physique théorique, unissant les techniques théoriques de terrain quantique utilisés en physique des particules et de la physique de la matière condensée dans un cadre théorique unique.
L'étude de la théorie quantique des champs est vivante et florissante, comme le sont les applications de cette méthode à de nombreux problèmes physiques. Il reste l'un des domaines les plus vitaux de physique théorique aujourd'hui, fournissant un langage commun à de nombreuses branches de la physique .
Principes de la théorie quantique des champs
Champs classiques et quantiques des champs
La mécanique quantique , dans sa formulation la plus générale, est une théorie de l'abstrait opérateurs (observables) agissant sur un espace d'état abstrait ( Espace de Hilbert), où les observables représentent des quantités physiquement observables et l'espace d'état représente les états possibles du système à l'étude. En outre, chaque observable correspond, dans un sens technique, à l'idée classique d'une degré de liberté. Par exemple, les observables fondamentales associées à la requête d'une seule particule de la mécanique quantique sont les opérateurs position et impulsion 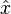 et
et 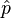 . La mécanique quantique ordinaires offres avec des systèmes de ce genre, qui possèdent un petit ensemble de degrés de liberté.
. La mécanique quantique ordinaires offres avec des systèmes de ce genre, qui possèdent un petit ensemble de degrés de liberté.
(Il est important de noter, à ce stade, que cet article ne utilise pas le mot " particule "dans le contexte de dualité onde-particule. En théorie quantique des champs, "particule" est un terme générique pour toute entité mécanique quantique discret, comme un électron, ce qui peut se comporter comme particules classiques ou vagues classiques dans différentes conditions expérimentales.)
Un champ quantique est un système mécanique quantique contenant une grande, et peut-être infini , le nombre de degrés de liberté. Ce ne est pas aussi exotique une situation qu'on pourrait le penser. Un champ classique contient un ensemble de degrés de liberté à chaque point de l'espace; par exemple, le classique champ électromagnétique définit deux vecteurs - le champ électrique et le champ magnétique - qui peuvent, en principe, prendre des valeurs distinctes pour chaque position  . Lorsque le champ dans son ensemble est considéré comme un système mécanique quantique, ses observables forment un infini (en fait, uncountable) ensemble, parce
. Lorsque le champ dans son ensemble est considéré comme un système mécanique quantique, ses observables forment un infini (en fait, uncountable) ensemble, parce  est continue.
est continue.
En outre, les degrés de liberté dans un champ quantique sont disposés en séries "répétées". Par exemple, les degrés de liberté dans un champ électromagnétique peuvent être regroupés en fonction de la position  , Avec exactement deux vecteurs pour chaque
, Avec exactement deux vecteurs pour chaque  . Notez que
. Notez que  est un nombre ordinaire qui "index" les observables; il est à ne pas confondre avec l'opérateur de position
est un nombre ordinaire qui "index" les observables; il est à ne pas confondre avec l'opérateur de position 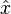 rencontré en mécanique quantique ordinaire, ce qui est une observable. (Ainsi, la mécanique quantique ordinaire est parfois appelés «théorie zéro-dimensionnel quantique des champs", car il ne contient qu'un seul ensemble d'observables.) Il est également important de noter qu'il n'y a rien de spécial
rencontré en mécanique quantique ordinaire, ce qui est une observable. (Ainsi, la mécanique quantique ordinaire est parfois appelés «théorie zéro-dimensionnel quantique des champs", car il ne contient qu'un seul ensemble d'observables.) Il est également important de noter qu'il n'y a rien de spécial  parce que, comme il se avère, il ya généralement plus d'une façon d'indexer les degrés de liberté dans le domaine.
parce que, comme il se avère, il ya généralement plus d'une façon d'indexer les degrés de liberté dans le domaine.
Dans les sections suivantes, nous allons montrer comment ces idées peuvent être utilisés pour construire une théorie de la mécanique quantique avec les propriétés souhaitées. Nous allons commencer par discuter une particule mécanique quantique et la théorie associée d'un grand nombre de particules mécanique quantique. Puis, en trouvant un moyen d'indexer les degrés de liberté dans le problème du nombre de particules, nous allons construire un champ quantique et d'étudier ses implications.
Single-particules et plusieurs particules mécanique quantique
En mécanique quantique ordinaire, le temps dépendant Équation de Schrödinger décrivant le mouvement d'une particule non relativiste est
où  est de la particule de masse ,
est de la particule de masse , 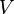 est l'appliqué potentiel, et
est l'appliqué potentiel, et 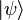 désigne le état quantique (nous utilisons Notation bra-ket).
désigne le état quantique (nous utilisons Notation bra-ket).
Nous voulons considérer comment ce problème se généralise à 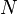 particules. Il ya deux motivations pour étudier le problème plusieurs particules. Le premier est un besoin simple dans la physique condensée de matière , où en général le nombre de particules est de l'ordre de nombre d'Avogadro (6.0221415 x 10 23). La deuxième motivation pour le problème plusieurs particules provient de la physique des particules et le désir d'intégrer les effets de la relativité restreinte . Si l'on tente d'inclure le relativiste énergie reste dans l'équation ci-dessus, le résultat est soit le Klein-Gordon équation ou le Équation de Dirac. Cependant, ces équations ont de nombreuses qualités insatisfaisants; par exemple, ils possèdent l'énergie valeurs propres qui se étendent sur -∞, de sorte qu'il semble y avoir aucune définition simple d'un état fondamental. Il se avère que ces incohérences proviennent de négliger la possibilité de créer ou de détruire les particules dynamique, ce qui est un aspect crucial de la relativité. Einstein célèbre rapport masse-énergie prédit que les particules suffisamment massives peuvent se désintégrer en plusieurs particules plus légères, et suffisamment particules énergétiques peuvent se combiner pour former des particules massives. Par exemple, un électron et un positron peut annihiler l'un l'autre pour créer des photons . Ainsi, une théorie quantique relativiste cohérent doit être formulée comme une théorie plusieurs particules.
particules. Il ya deux motivations pour étudier le problème plusieurs particules. Le premier est un besoin simple dans la physique condensée de matière , où en général le nombre de particules est de l'ordre de nombre d'Avogadro (6.0221415 x 10 23). La deuxième motivation pour le problème plusieurs particules provient de la physique des particules et le désir d'intégrer les effets de la relativité restreinte . Si l'on tente d'inclure le relativiste énergie reste dans l'équation ci-dessus, le résultat est soit le Klein-Gordon équation ou le Équation de Dirac. Cependant, ces équations ont de nombreuses qualités insatisfaisants; par exemple, ils possèdent l'énergie valeurs propres qui se étendent sur -∞, de sorte qu'il semble y avoir aucune définition simple d'un état fondamental. Il se avère que ces incohérences proviennent de négliger la possibilité de créer ou de détruire les particules dynamique, ce qui est un aspect crucial de la relativité. Einstein célèbre rapport masse-énergie prédit que les particules suffisamment massives peuvent se désintégrer en plusieurs particules plus légères, et suffisamment particules énergétiques peuvent se combiner pour former des particules massives. Par exemple, un électron et un positron peut annihiler l'un l'autre pour créer des photons . Ainsi, une théorie quantique relativiste cohérent doit être formulée comme une théorie plusieurs particules.
En outre, nous allons supposer que le 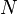 particules sont indiscernables. Comme il est décrit dans l'article sur particules identiques, ce qui implique que l'état de l'ensemble du système doit être soit symétrique ( bosons) ou antisymétrique ( fermions) lorsque les coordonnées de ses particules constitutives sont échangés. Ces états multi-particules sont assez compliquées à écrire. Par exemple, l'état quantique d'un système général de
particules sont indiscernables. Comme il est décrit dans l'article sur particules identiques, ce qui implique que l'état de l'ensemble du système doit être soit symétrique ( bosons) ou antisymétrique ( fermions) lorsque les coordonnées de ses particules constitutives sont échangés. Ces états multi-particules sont assez compliquées à écrire. Par exemple, l'état quantique d'un système général de 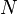 bosons se écrit
bosons se écrit
où 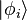 sont les états à une particule,
sont les états à une particule,  est le nombre de particules Etat occupant
est le nombre de particules Etat occupant 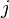 Et la somme est calculée sur tous les possibles permutations
Et la somme est calculée sur tous les possibles permutations 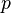 agissant sur
agissant sur 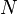 éléments. En général, ce est une somme de
éléments. En général, ce est une somme de  (
( 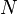 factorielle ) Les termes distincts, ce qui devient vite ingérable
factorielle ) Les termes distincts, ce qui devient vite ingérable 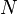 augmente. Le moyen de simplifier ce problème est d'en faire une théorie quantique des champs.
augmente. Le moyen de simplifier ce problème est d'en faire une théorie quantique des champs.
Deuxième quantification
Dans cette section, nous allons décrire une méthode pour construire une théorie quantique des champs appelé seconde quantification. Il se agit essentiellement de choisir une façon d'indexer les degrés de liberté de la mécanique quantique en l'espace de plusieurs états-particules identiques. Il est basé sur la Formulation hamiltonien de la mécanique quantique; plusieurs autres approches existent, comme le Feynman chemin intégrante, qui utilise une Formulation lagrangienne. Pour un aperçu, voir l'article sur quantification.
Seconde quantification de bosons
Pour plus de simplicité, nous allons d'abord discuter de seconde quantification pour bosons, qui forment états quantiques parfaitement symétriques. Notons les États unique de particules mutuellement orthogonaux par 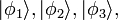 et ainsi de suite. Par exemple, l'état 3-particule avec une particule dans l'état
et ainsi de suite. Par exemple, l'état 3-particule avec une particule dans l'état 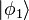 et deux dans l'état
et deux dans l'état 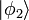 est
est
La première étape de la seconde quantification est d'exprimer ces états quantiques en termes de nombres d'occupation, en énumérant le nombre de particules occupant chacun des états à une particule  etc. Ce est simplement une autre façon d'étiqueter les Etats. Par exemple, l'état de particules 3 ci-dessus est désignée par
etc. Ce est simplement une autre façon d'étiqueter les Etats. Par exemple, l'état de particules 3 ci-dessus est désignée par
L'étape suivante consiste à étendre le 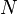 espace -particle de l'Etat à inclure les espaces de l'État pour toutes les valeurs possibles de
espace -particle de l'Etat à inclure les espaces de l'État pour toutes les valeurs possibles de 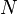 . Cet espace d'état étendu, connu sous le nom Espace de Fock, est composé de l'espace d'état d'un système sans particules (le soi-disant état de vide), plus l'espace d'état d'un système 1-particules, plus l'espace d'état d'un système 2-particules, et ainsi de suite. Il est facile de voir qu'il ya une correspondance un-à-un entre la représentation de nombre d'occupation et les Etats bosons valables dans l'espace Fock.
. Cet espace d'état étendu, connu sous le nom Espace de Fock, est composé de l'espace d'état d'un système sans particules (le soi-disant état de vide), plus l'espace d'état d'un système 1-particules, plus l'espace d'état d'un système 2-particules, et ainsi de suite. Il est facile de voir qu'il ya une correspondance un-à-un entre la représentation de nombre d'occupation et les Etats bosons valables dans l'espace Fock.
À ce stade, le système mécanique quantique est devenue un champ quantique dans le sens que nous avons décrit ci-dessus. Degrés élémentaires du domaine de la liberté sont les nombres d'occupation, et chaque nombre d'occupation est indexé par un certain nombre 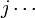 , Indiquant lequel des états à une particule
, Indiquant lequel des états à une particule 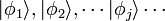 il se réfère.
il se réfère.
Les propriétés de ce champ quantique peuvent être explorées en définissant création et d'annihilation opérateurs, qui ajoutent et les particules de la soustraction. Ils sont analogues aux «opérateurs d'échelle" dans le problème de oscillateur harmonique quantique, qui a ajouté et soustrait quanta d'énergie. Toutefois, ces opérateurs créent littéralement et annihilent des particules d'un état quantique donné. L'opérateur d'annihilation de bosons 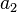 et exploitant de création
et exploitant de création 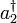 avoir les effets suivants:
avoir les effets suivants:
On peut montrer que ce sont les opérateurs dans le sens de la mécanique quantique d'habitude, ce est à dire opérateurs linéaires agissant sur l'espace de Fock. En outre, ils sont en effet Conjugués hermitiques, ce qui justifie la façon dont nous les avons écrite. Ils peuvent être présentés à obéir à la relation de commutation
où 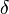 Supports pour les Kronecker. Ce sont précisément les relations obéi par les opérateurs d'échelle pour un ensemble infini de indépendante oscillateurs harmoniques quantiques, une pour chaque état à une particule. Ajout ou suppression de bosons de chaque Etat est donc analogue à excitant ou de-excitation d'un quantum d'énergie dans un oscillateur harmonique.
Supports pour les Kronecker. Ce sont précisément les relations obéi par les opérateurs d'échelle pour un ensemble infini de indépendante oscillateurs harmoniques quantiques, une pour chaque état à une particule. Ajout ou suppression de bosons de chaque Etat est donc analogue à excitant ou de-excitation d'un quantum d'énergie dans un oscillateur harmonique.
Le Hamiltonien du champ quantique (qui, par la Équation de Schrödinger, détermine sa dynamique) peuvent être écrites en termes d'opérateurs de création et d'annihilation. Par exemple, l'hamiltonien d'un champ de libres (sans interaction) est bosons
où 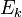 est l'énergie de la
est l'énergie de la 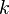 ième une particule état propre de l'énergie. Notez que
ième une particule état propre de l'énergie. Notez que
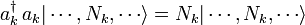 .
.
Seconde quantification de fermions
Il se avère que une définition différente de la création et l'annihilation doit être utilisé pour décrire fermions. Selon le Principe d'exclusion de Pauli, fermions ne peut pas partager états quantiques, de sorte que leurs nombres d'occupation 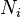 ne peut prendre la valeur 0 ou 1. Les opérateurs d'annihilation fermioniques
ne peut prendre la valeur 0 ou 1. Les opérateurs d'annihilation fermioniques  et opérateurs de création
et opérateurs de création 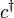 sont définis par
sont définis par
Ces obéir à un relation de anticommutation:
On peut remarquer à partir de ce que l'application d'un opérateur de création fermionique donne deux fois zéro, de sorte qu'il est impossible pour les particules à part les Etats à particule unique, en conformité avec le principe d'exclusion.
Les opérateurs terrain
Nous avons déjà mentionné qu'il peut y avoir plus d'une façon d'indexer les degrés de liberté dans un champ quantique. Deuxième indices de quantification du terrain par l'énumération des états quantiques à particule unique. Cependant, comme nous l'avons vu, il est plus naturel de penser à un «champ», comme le champ électromagnétique, comme un ensemble de degrés de liberté indexé par la position.
À cette fin, nous pouvons définir des opérateurs de terrain qui créent ou détruisent une particule à un point particulier dans l'espace. En physique des particules, ces opérateurs se avèrent être plus commode de travailler avec, parce qu'ils facilitent de formuler des théories qui satisfont aux exigences de la relativité.
États particules uniques sont généralement énumérés en fonction de leur moments (comme dans le particule dans un problème de boîte.) Nous pouvons construire des opérateurs de terrain en appliquant la Transformée de Fourier aux opérateurs de création et d'annihilation de ces Etats. Par exemple, l'opérateur d'annihilation champ bosonique 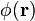 est
est
Les opérateurs de terrain bosoniques obéissent à la relation de commutation
où 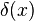 Supports pour les Fonction de Dirac. Comme précédemment, les relations fermioniques sont les mêmes, avec les commutateurs remplacés par anticommutators.
Supports pour les Fonction de Dirac. Comme précédemment, les relations fermioniques sont les mêmes, avec les commutateurs remplacés par anticommutators.
Il convient de souligner que l'opérateur de champ ne est pas la même chose que d'une fonction d'onde mono-particules. Le premier est un opérateur agissant sur l'espace de Fock, et celui-ci est juste un champ scalaire. Cependant, ils sont étroitement liés, et sont en effet couramment désignées par le même symbole. Si nous avons un hamiltonien avec une représentation de l'espace, dire
où les indices 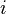 et
et 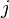 courir sur toutes les particules, puis l'hamiltonien de la théorie des champs est
courir sur toutes les particules, puis l'hamiltonien de la théorie des champs est
Ce ressemble remarquablement à une expression de la valeur moyenne de l'énergie, avec 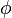 jouant le rôle de la fonction d'onde. Cette relation entre les opérateurs sur le terrain et des fonctions d'onde, il est très facile de formuler des théories sur le terrain à partir de Hamilton projetée dans l'espace.
jouant le rôle de la fonction d'onde. Cette relation entre les opérateurs sur le terrain et des fonctions d'onde, il est très facile de formuler des théories sur le terrain à partir de Hamilton projetée dans l'espace.
Implications de la théorie quantique des champs
Unification des champs et des particules
La procédure "seconde de quantification" que nous avons décrit dans la section précédente prend un ensemble d'états quantiques à particule unique comme point de départ. Parfois, il est impossible de définir ces états à une particule, et l'on doit se rendre directement à la théorie quantique des champs. Par exemple, une théorie quantique de la champ électromagnétique doit être une théorie quantique des champs, car il est impossible (pour diverses raisons) pour définir une fonction d'onde pour un seul photon . Dans de telles situations, la théorie quantique des champs peut être construit en examinant les propriétés mécaniques du domaine classique et deviner le la théorie quantique correspondant. Les théories quantiques des champs obtenus de cette façon ont les mêmes propriétés que celles obtenues en utilisant la seconde quantification, cette création bien défini et opérateurs d'annihilation obéissant commutation ou anticommutation relations.
Théorie quantique des champs fournit donc un cadre unifié pour décrire les objets "sur le terrain-like" (tels que le champ électromagnétique, dont les excitations sont photons) et des objets "de particules-like" (telles que des électrons, qui sont traités comme des excitations d'un champ électronique sous-jacente ).
Signification physique de indiscernabilité des particules
La seconde procédure de quantification dépend essentiellement de particules étant identiques. Nous ne aurions pas été en mesure de construire une théorie quantique des champs d'un système plusieurs particules distinguer, car il n'y aurait pas eu moyen de séparer et en indexant les degrés de liberté.
Beaucoup de physiciens préfèrent prendre l'interprétation inverse, qui est que la théorie quantique des champs, explique ce que sont les particules identiques. En mécanique quantique ordinaire, il ne ya pas beaucoup de motivation théorique de l'utilisation symétrique (bosons) ou des états antisymétriques (fermions), et la nécessité pour ces pays est tout simplement considéré comme un fait empirique. Du point de vue de la théorie quantique des champs, les particules sont identiques si et seulement si ils sont excitations du même champ quantique sous-jacent. Ainsi, la question «pourquoi sont tous les électrons identiques?" provient de tort au sujet électrons individuels comme des objets fondamentaux, alors qu'en fait ce ne est que le champ d'électrons qui est fondamental.
conservation de particules et non-conservation
Au cours de la seconde quantification, nous avons commencé avec un espace de hamiltonien et état décrivant un nombre fixe de particules ( 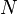 ), Et se est terminée avec un hamiltonien et de l'espace de l'Etat pour un nombre arbitraire de particules. Bien sûr, dans de nombreuses situations ordinaires
), Et se est terminée avec un hamiltonien et de l'espace de l'Etat pour un nombre arbitraire de particules. Bien sûr, dans de nombreuses situations ordinaires 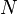 est une quantité importante et parfaitement bien définie, par exemple, si nous décrivons un gaz atomes scellés dans une boîte. Du point de vue de la théorie quantique des champs, de telles situations sont décrites par les états quantiques qui sont des états propres de la opérateur de numéro
est une quantité importante et parfaitement bien définie, par exemple, si nous décrivons un gaz atomes scellés dans une boîte. Du point de vue de la théorie quantique des champs, de telles situations sont décrites par les états quantiques qui sont des états propres de la opérateur de numéro  , Qui mesure le nombre total de particules présentes. Comme pour toute observable de la mécanique quantique,
, Qui mesure le nombre total de particules présentes. Comme pour toute observable de la mécanique quantique,  est conservée si elle commute avec l'hamiltonien. Dans ce cas, l'état quantique est piégé dans le
est conservée si elle commute avec l'hamiltonien. Dans ce cas, l'état quantique est piégé dans le 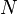 -particle sous-espace de l'espace de Fock totale, et la situation pourrait tout aussi bien être décrit par ordinaire
-particle sous-espace de l'espace de Fock totale, et la situation pourrait tout aussi bien être décrit par ordinaire 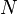 la mécanique quantique -particle.
la mécanique quantique -particle.
Par exemple, nous pouvons voir que l'hamiltonien libre de Higgs décrit ci-dessus conserve nombre de particules. Chaque fois que l'hamiltonien fonctionne sur un état, chaque particule détruite par un opérateur d'annihilation  est immédiatement remis par l'opérateur de création
est immédiatement remis par l'opérateur de création  .
.
D'autre part, il est possible, et même commune, de rencontrer des états quantiques qui ne sont pas états propres de  Qui ne ont pas un nombre de particules bien définies. Ces états sont difficiles ou impossibles à gérer en utilisant la mécanique quantique ordinaires, mais ils peuvent être facilement décrits dans la théorie quantique des champs que superpositions quantiques des Etats ayant des valeurs différentes de
Qui ne ont pas un nombre de particules bien définies. Ces états sont difficiles ou impossibles à gérer en utilisant la mécanique quantique ordinaires, mais ils peuvent être facilement décrits dans la théorie quantique des champs que superpositions quantiques des Etats ayant des valeurs différentes de 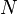 . Par exemple, supposons que nous ayons un champ bosonique dont les particules peuvent être créés ou détruits par des interactions avec un champ fermionique. Le hamiltonien du système combiné serait donnée par les hamiltoniens du boson libre et les champs de fermions libres, plus une "énergie potentielle" terme comme
. Par exemple, supposons que nous ayons un champ bosonique dont les particules peuvent être créés ou détruits par des interactions avec un champ fermionique. Le hamiltonien du système combiné serait donnée par les hamiltoniens du boson libre et les champs de fermions libres, plus une "énergie potentielle" terme comme
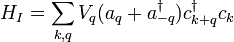 ,
,
où  et
et  désigne les opérateurs de création et d'annihilation de bosons,
désigne les opérateurs de création et d'annihilation de bosons, 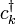 et
et 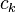 désigne les opérateurs de création et d'annihilation de fermions, et
désigne les opérateurs de création et d'annihilation de fermions, et 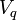 est un paramètre qui décrit la force de l'interaction. Cette «terme d'interaction" décrit les processus dans lequel un fermion dans l'état
est un paramètre qui décrit la force de l'interaction. Cette «terme d'interaction" décrit les processus dans lequel un fermion dans l'état 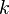 soit absorbe ou émet un boson, étant ainsi un coup de pied dans un état propre différente
soit absorbe ou émet un boson, étant ainsi un coup de pied dans un état propre différente 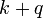 . (En fait, ce type de hamiltonien est utilisé pour décrire l'interaction entre électrons de conduction et phonons dans les métaux . L'interaction entre des électrons et des photons est traité d'une manière similaire, mais est un peu plus compliqué, car le rôle de pirouette doit être prise en compte.) Une chose à noter ici est que même si nous commençons avec un nombre fixe de bosons, nous allons généralement retrouver avec une superposition d'états avec des nombres différents de bosons à des moments plus tard. Le nombre de fermions, cependant, est conservée dans ce cas.
. (En fait, ce type de hamiltonien est utilisé pour décrire l'interaction entre électrons de conduction et phonons dans les métaux . L'interaction entre des électrons et des photons est traité d'une manière similaire, mais est un peu plus compliqué, car le rôle de pirouette doit être prise en compte.) Une chose à noter ici est que même si nous commençons avec un nombre fixe de bosons, nous allons généralement retrouver avec une superposition d'états avec des nombres différents de bosons à des moments plus tard. Le nombre de fermions, cependant, est conservée dans ce cas.
En matière condensée , précise avec des numéros de particules mal définis sont particulièrement importantes pour décrire les différents superfluides. Beaucoup des caractéristiques déterminantes d'un superfluide découlent de l'idée que son état quantique est une superposition d'états avec des nombres de particules différentes.
Approches axiomatiques
La description précédente de la théorie quantique des champs suit l'esprit dans lequel la plupart physiciens abordent le sujet. Cependant, il ne est pas mathématiquement rigoureuse. Au cours des dernières décennies, il ya eu de nombreuses tentatives pour mettre la théorie quantique des champs sur une base mathématique cabinet en formulant un ensemble de axiomes pour elle. Ces tentatives se répartissent en deux grandes catégories.
La première classe d'axiomes, d'abord proposé au cours de la 1950, inclure le Wightman, Osterwalder-Schrader, et Systèmes Haag-Kastler. Ils ont tenté de formaliser la notion d'un «champ de l'opérateur-évalué" des physiciens dans le cadre de analyse fonctionnelle, et un succès limité apprécié. Il était possible de prouver que toute théorie quantique des champs satisfaire ces axiomes satisfait certains théorèmes généraux, tels que le Théorème spin-statistique et de la Théorème CPT. Malheureusement, il se est avéré extrêmement difficile de montrer que toute la théorie du champ réaliste, y compris le modèle standard , satisfait ces axiomes. La plupart des théories qui pourraient être traitées avec ces axiomes analytiques étaient physiquement trivial, être limité à de faibles dimensions et manquant dynamique intéressante. La construction de théories qui satisfont l'un de ces ensembles d'axiomes tombe dans le domaine de théorie quantique des champs constructive. Un travail important a été fait dans ce domaine dans le 1970 par Segal, Glimm, Jaffe et autres.
Pendant le 1980, une deuxième série d'axiomes sur la base géométriques idées a été proposé. Cette ligne d'enquête, ce qui limite son attention à une classe particulière des théories quantiques des champs appelés théories topologiques des champs quantiques, est associé le plus étroitement avec Michael Atiyah et Graeme Segal, et a notamment été complétée par des Edward Witten, Richard Borcherds, et Maxim Kontsevich. Cependant, les théories quantiques des champs les plus physiquement pertinents, tels que le modèle standard , ne sont pas les théories topologiques des champs quantiques; la théorie quantique du champ effet Hall quantique fractionnaire est une exception notable. Le principal impact de la théorie du champ quantique topologique axiomatique a été mis sur les mathématiques, avec d'importantes applications dans théorie de la représentation, topologie algébrique et la géométrie différentielle .
Trouver les axiomes appropriés pour la théorie quantique des champs est encore un problème ouvert et difficile en mathématiques. L'un des Prix de Millénium de problèmes-prouver l'existence d'un écart de masse dans la théorie de Yang-Mills-est lié à cette question.
Phénomènes associés à la théorie quantique des champs
Dans la partie précédente de l'article, nous avons décrit les propriétés les plus générales de théories quantiques des champs. Certaines des théories quantiques des champs étudiés dans divers domaines de la physique théorique possèdent des propriétés spéciales supplémentaires, tels que renormalisabilité, symétrie de jauge et la supersymétrie. Ceux-ci sont décrits dans les sections suivantes.
Renormalisation
Tôt dans l'histoire de la théorie quantique des champs, il a été constaté que de nombreux calculs apparemment inoffensifs, tels que le perturbative changement dans l'énergie d'un électron en raison de la présence du champ électromagnétique, donnent des résultats infinis. Beaucoup de ces problèmes sont liés à des défaillances dans électrodynamique classique qui ont été identifiés (mais non résolus) aussi loin que le 19ème siècle , et elles proviennent essentiellement du fait que la plupart des propriétés soi-disant «intrinsèques» d'un électron sont liés au champ électromagnétique avec lequel il interagit. Pour illustrer cela, le rappel de la discussion précédente que le hamiltonien d'interaction entre deux champs quantiques, comme le champ d'électrons et le champ électromagnétique, n'a pas besoin de conserver le nombre de particules. Ainsi, même si nous commençons avec un seul électron et aucun photons, l'état quantique va évoluer rapidement dans une superposition d'états qui peuvent inclure un ou plusieurs photons. Par conséquent, l'énergie transportée par ce "single" électron-son auto-énergie ne est pas simplement la valeur «nu», mais comprend également l'énergie contenue dans un nuage agent de photons. Lorsque cette énergie auto est calculé, on constate que la contribution des énergies photons possédant arbitrairement élevées (ou, de façon équivalente, arbitrairement courte longueurs d'onde) conduit à une valeur infinie formellement.
La solution à ce problème, d'abord donnée par Julian Schwinger, est appelé renormalisation . L'idée est d'imposer une " coupure "pour la contribution photonique, par exemple en postulant que les photons ne peuvent pas posséder des énergies dépassant une certaine valeur extrêmement élevée. Toute quantité nous souhaitons calculer, tels que l'énergie reste, est maintenant fini, mais dépend de la coupure. Nous avons ensuite refondre le résultat en termes des quantités de physiquement observables comme la masse de l'électron observée, à la place de quantités non observables tels que l'énergie de coupure et de la masse de l'électron nu. Le résultat final est indépendant de tous les détails de la procédure de coupure, y compris la valeur de l'énergie de coupure, à condition que le processus pertinents se produisent à des énergies bien en dessous du seuil.
La procédure de renormalisation ne fonctionne que pour une certaine classe de théories quantiques des champs, appelé théories quantiques des champs renormalisables. Le modèle standard de la physique des particules est renormalisable, et sont donc ses théories de composants ( électrodynamique quantique / théorie électrofaible et chromodynamique quantique). Selon la théorie de la groupe de renormalisation, chaque théorie renormalisable une limite basse énergie unique (à savoir ce qu'on appelle un " théorie effective sur le terrain ») pour un large éventail de théories de haute énergie. renormalisable théories sont donc indépendante de la nature précise des phénomènes de haute énergie sous-jacents.
la liberté de la jauge
Un théorie de jauge est une théorie qui admet une symétrie avec un paramètre local. Par exemple, dans tous les quantique théorie mondial phase de la fonction d'onde est arbitraire et ne représente pas quelque chose de physique. Par conséquent, la théorie est invariante par un changement global de phases (ajout d'une constante à la phase de toutes les fonctions d'ondes, partout); c'est un symétrie globale. En électrodynamique quantique, la théorie est aussi invariant par un changement local de la phase, ce est - on peut décaler la phase de tous fonctions d'onde de sorte que le changement peut être différente en tout point l'espace-temps. C'est un symétrie locale. Cependant, pour qu'un bien définie dérivé opérateur existe, il faut introduire une nouvelle domaine, la champ de jauge, qui transforme aussi pour que le changement de variables locales (la phase dans notre exemple) ne pas affecter le dérivé. En électrodynamique quantique ce champ de jauge est le champ électromagnétique. La rupture de charge locale de variables est appelé transformation de jauge.
En théorie quantique des champs les excitations de champs représentent particules. La particule associée à des excitations de la champ de jauge est le boson de jauge, qui est le photon dans le cas de électrodynamique quantique.
Le degrés de liberté en théorie quantique des champs sont fluctuations locales des champs. L'existence d'un symétrie de jauge réduit le nombre de degrés de liberté, tout simplement parce que des fluctuations des champs peuvent être transformés à zéro par évaluer transformations, de sorte qu'ils sont équivalents à ne pas avoir les fluctuations du tout, et ils ne ont donc aucune signification physique. Ces fluctuations sont généralement appelés "degrés non-physiques de la liberté" ou des artefacts de jauge; habituellement certains d'entre eux ont une négative Norm, ce qui les rend inadéquat pour une théorie cohérente. Par conséquent, si une théorie du champ classique a une symétrie de jauge, puis sa version quantifiée (à savoir la théorie quantique des champs correspondant) aura cette symétrie. En d'autres termes, une symétrie de jauge ne peut pas avoir un quantum anomalie. Si une symétrie de jauge est anormale (c.-à-pas gardé dans la théorie quantique) alors la théorie est non-conforme: par exemple, dans l'électrodynamique quantique, il y avait eu une jauge anomalie, cela nécessiterait l'apparition de photons avec longitudinale polarisation et polarisation dans le temps direction, celui-ci ayant un négatif norme, ce qui rend incompatible la théorie; une autre possibilité serait pour ces photons apparaissent uniquement dans les processus intermédiaires, mais pas dans les produits finaux de toute interaction, ce qui rend la théorie non unitaire et encore incompatibles (voir théorème optique).
En général, la transformations de jauge d'une théorie consistent plusieurs transformations différentes, qui peuvent ne pas être commutative . Ces transformations sont ainsi décrites par un objet mathématique connu comme un groupe de jauge. infinitésimales transformations de jauge sont le groupe de jauge générateurs. Par conséquent, le nombre de bosons de jauge est le groupe dimension (nombre de générateurs formant une base).
Tous les interactions fondamentales de la nature sont décrits par théorie de jauge. Ceux-ci sont:
- Électrodynamique quantique, dontla transformation jauge est un changement local de la phase, de sorte que legroupe de jauge estU (1). Le boson de jauge est lephoton.
- Chromodynamique quantique, dontle groupe est la jauge SU (3). Le bosons de jauge sont huit gluons.
- Le Théorie électrofaible, dont legroupe jauge est
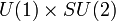 (A produit direct deU (1) etSU (2)).
(A produit direct deU (1) etSU (2)). - Gravity, dont la théorie classique estla relativité générale, admet le principe d'équivalence, qui est une forme de symétrie de jauge.
Supersymétrie
Supersymétrie suppose que chaque fondamentale fermion a une superpartenaire qui est un boson et vice versa. Il a été introduit afin de résoudre le soi-disant problème de hiérarchie, qui est, pour expliquer pourquoi les particules ne sont protégés par aucune symétrie (comme le boson de Higgs) ne reçoivent pas les corrections radiatives à sa masse le conduire aux plus grandes échelles (GUT, Planck ...). Il a été vite réalisé que la supersymétrie a d'autres propriétés intéressantes: sa version calibrée est une extension de la relativité générale ( Supergravity), et il est un ingrédient clé de la cohérence de la théorie des cordes .
La façon supersymmetry protège les hiérarchies est la suivante: étant donné que pour chaque particule il ya un superpartenaire avec la même masse, toute boucle dans une correction radiative est annulée par la boucle correspondant à sa superpartenaire, ce qui rend le fini théorie UV.
Depuis aucun superpartenaires n'a encore été observée, si la supersymétrie existe, il doit être rompu (par un terme douce dite, qui rompt la supersymétrie sans ruiner ses fonctionnalités utiles). Les modèles les plus simples de cette rupture exigent que l'énergie des superpartenaires pas être trop élevé; dans ces cas, la supersymétrie devrait être observé par des expériences à la Grand collisionneur de hadrons.

![\ Left [\ frac {| \ mathbf {p} | ^ 2} {} 2m + V (\ mathbf {r}) \ right] | \ psi (t) \ rang = i \ hbar \ frac {\ partial} { \ partial t} | \ psi (t) \ rang,](../../images/261/26195.png)
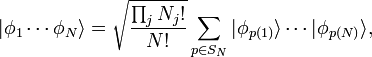
![\ Frac {1} {\ sqrt {3}} \ left [| \ phi_1 \ rang | \ phi_2 \ rang | \ phi_2 \ rang + | \ phi_2 \ rang | \ phi_1 \ rang | \ phi_2 \ rang + | \ phi_2 \ rang | \ phi_2 \ rang | \ phi_1 \ rang \ right].](../../images/262/26203.png)
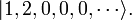
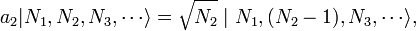
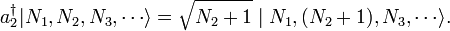
![\ Left [a_i, a_j \ right] = 0 \ quad, \ quad \ left [a_i ^ \ poignard, a_j ^ \ poignard \ right] = 0 \ quad, \ quad \ left [a_i, a_j ^ \ poignard \ right] = \ {ij} delta_,](../../images/262/26211.png)
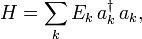
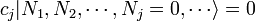

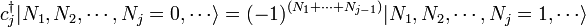
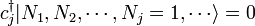
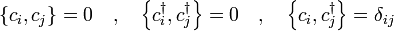
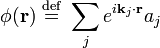
![\ Left [\ phi (\ mathbf {r}), \ phi (\ mathbf {r '}) \ right] = 0 \ quad, \ quad \ left [\ phi ^ \ dagger (\ mathbf {r}), \ phi ^ \ dagger (\ mathbf {r '}) \ right] = 0 \ quad, \ quad \ left [\ phi (\ mathbf {r}), \ phi ^ \ dagger (\ mathbf {r'}) \ right ] = \ delta ^ 3 (\ mathbf {r} - \ mathbf {r '})](../../images/262/26222.png)