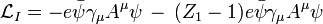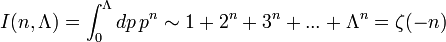Renormalisation
Renseignements généraux
Cette sélection Wikipedia est déconnecté disponibles à partir enfants SOS pour la distribution dans le monde en développement. parrainage SOS enfant est cool!
| Théorie quantique des champs |
|---|
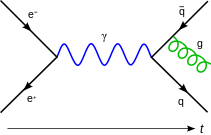 Diagramme de Feynman |
| Histoire |
Fond
|
Symétries
|
Outils
|
Équations
|
|
|
Théories incomplètes
|
Les scientifiques
|
Dans la théorie quantique des champs , les mécanique statistique des champs, et la théorie de structures géométriques auto-similaires, renormalisation se réfère à un ensemble de techniques utilisées pour prendre une limite continue.
En décrivant l'espace et le temps comme un continuum, certaines constructions mécaniques statistiques et quantiques sont mal définis. Pour les définir, la limite de continuum doit être pris avec précaution.
Renormalisation détermine la relation entre les paramètres dans la théorie, lorsque les paramètres décrivant les grandes échelles de distance diffèrent des paramètres décrivant petites distances. Renormalisation a été élaboré en électrodynamique quantique (QED) de donner un sens infini dans intégrales la théorie des perturbations. Initialement considéré comme un suspect, la procédure provisoire par certains de ses initiateurs, renormalisation a finalement été embrassé comme un important et outil d'auto-cohérent dans plusieurs domaines de la physique et les mathématiques .
Auto-interactions dans la physique classique

Le problème des infinis a pris naissance dans le électrodynamique classique de particules ponctuelles dans le 19ème et début du 20ème siècle.
La masse d'une particule chargée devrait inclure la masse-énergie dans son champ électrostatique. On suppose que la particule est une coque sphérique de rayon accusé  . L'énergie dans le domaine est
. L'énergie dans le domaine est
et il est infinie lorsque  est zéro. La valeur de
est zéro. La valeur de  qui fait
qui fait 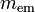 égale à la masse de l'électron est appelé le Électron. Avec des facteurs de c et
égale à la masse de l'électron est appelé le Électron. Avec des facteurs de c et 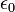 restaurée:
restaurée:
Il est donc  fois plus petite que la Compton longueur d'onde de l'électron.
fois plus petite que la Compton longueur d'onde de l'électron.
La masse d'une particule chargée sphérique comprend la masse de l'enveloppe sphérique. Si la masse de la coquille est autorisé à être négatif, il pourrait être possible de prendre un point limite cohérente. Cela a été appelé renormalisation, et Lorentz et Abraham a tenté de développer une théorie classique de l'électron de cette façon. Ces premiers travaux a été la source d'inspiration pour les tentatives ultérieures à régularisation et renormalisation en théorie quantique des champs.
Lors du calcul des électromagnétiques interactions de charge des particules, il est tentant d'ignorer l'arrière-réaction de son propre champ d'une particule sur elle-même. Mais cette réaction arrière est nécessaire d'expliquer le frottement sur les particules chargées quand ils émettent un rayonnement. Si l'électron est supposé être un point, la valeur de la contre-réaction se écarte, pour la même raison que la masse se écarte, car le champ est l'inverse du carré.
Le Théorie Abraham-Lorentz avait un "pré-accélération" non causale. Parfois, un électron serait commencer à bouger avant que la force est appliquée. Ce est un signe que la limite de points est incompatible. Un corps étendu commencera à se déplacer lorsqu'une force est appliquée dans une rayon de centre de masse.
Le problème était pire dans la théorie du champ classique que dans la théorie quantique des champs, car en théorie quantique des champs une particule chargée à courte distance peut fluctuer dans une antiparticule. Le antiparticule a une charge opposée, et les fluctuations frottis sur la charge sur une région comparable à la longueur d'onde Compton. En électrodynamique quantique à petit couplage électromagnétique de la masse ne diverge que le journal du rayon de la particule.
Beaucoup de physiciens croient que lorsque la constante de structure fine est bien supérieur à un, de sorte que le rayon classique de l'électron est plus grande que la longueur d'onde quantique, les mêmes problèmes qui affligent l'électrodynamique classique sont encore présents dans l'électrodynamique quantique.
Divergences dans l'électrodynamique quantique

Lors du développement de l'électrodynamique quantique dans les années 1930, Max Born, Werner Heisenberg, Pascual Jordan et Paul Dirac ont découvert que dans les calculs perturbatifs nombreuses intégrales étaient divergentes.
Une façon de décrire les divergences a été découvert dans les années 1930 par Ernst Stueckelberg, dans les années 1940 par Julian Schwinger, Richard Feynman , et Shin'ichiro Tomonaga, et systématisé par Freeman Dyson. Les divergences apparaissent dans les calculs impliquant Diagrammes de Feynman avec boucles fermées de dans les particules virtuelles.
Tandis que les particules virtuelles obéissent conservation de l'énergie et l'élan , ils peuvent avoir toute l'énergie et l'élan, même celui qui ne est pas autorisé par la relation relativiste énergie-impulsion pour la masse de cette particule observée. (C'est,  ne est pas nécessairement la masse de la particule par le fait que le procédé (par exemple pour un photon, il pourrait être différente de zéro).) Une telle particule est appelée hors-coquille. Quand il ya une boucle, la dynamique des particules impliquées dans la boucle ne est pas uniquement déterminé par les énergies et les moments de particules entrants et sortants. Une variation de l'énergie d'une particule dans la boucle peut être contrebalancée par une variation égale et opposée à l'énergie d'une autre particule dans la boucle. Donc, pour trouver l'amplitude pour le processus de boucle il faut intégrer sur toutes les combinaisons possibles de l'énergie et l'élan qui pourrait voyager autour de la boucle.
ne est pas nécessairement la masse de la particule par le fait que le procédé (par exemple pour un photon, il pourrait être différente de zéro).) Une telle particule est appelée hors-coquille. Quand il ya une boucle, la dynamique des particules impliquées dans la boucle ne est pas uniquement déterminé par les énergies et les moments de particules entrants et sortants. Une variation de l'énergie d'une particule dans la boucle peut être contrebalancée par une variation égale et opposée à l'énergie d'une autre particule dans la boucle. Donc, pour trouver l'amplitude pour le processus de boucle il faut intégrer sur toutes les combinaisons possibles de l'énergie et l'élan qui pourrait voyager autour de la boucle.
Ces intégrales sont souvent divergente, ce qui signifie qu'ils donnent des réponses infinite. Les divergences qui sont importants sont les " ultraviolets "(UV) ones. Une divergence ultraviolette peuvent être décrits comme une qui provient de
- - Dans la région de l'intégrale où toutes les particules dans la boucle ont de grandes énergies et l'élan.
- - Très court longueurs d'onde et haute fréquences fluctuations des champs, dans le intégrale de chemin pour le champ.
- - Très court temps voulu entre les émissions de particules et d'absorption, si la boucle est considérée comme une somme sur des chemins de particules.
Donc, ces divergences sont à courte distance, les phénomènes de courte durée.
Il ya exactement trois une boucle diagrammes de boucles divergente dans l'électrodynamique quantique.
- un photon d'électrons crée un virtuel tomographie par paire qui annihilent ensuite, ce est un schéma de polarisation du vide.
- un électron qui émet un photon et résorbe rapidement virtuel, appelé une auto-énergie.
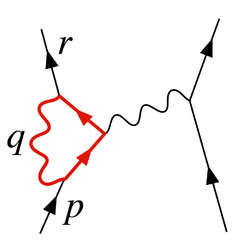
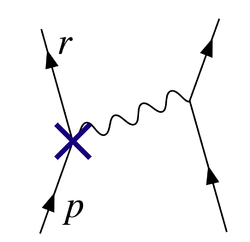
- Un électron émet un photon, émet un deuxième photon, et résorbe le premier. Ce processus est illustré à la figure 2, et il est appelé un sommet de renormalisation.
Les trois écarts correspondent aux trois paramètres de la théorie:
- le champ de normalisation Z.
- la masse de l'électron.
- la charge de l'électron.
Une seconde classe de divergence, appelée divergence infrarouge, est due à des particules sans masse, comme le photon. Chaque processus impliquant des particules chargées émet une infinité de photons cohérents de longueur d'onde infinie, et l'amplitude pour émettre un nombre quelconque de photons est zéro. Pour photons, ces divergences sont bien compris et ne sont pas une source de controverse.
Une divergence de boucle
Le schéma de la figure 2 montre une des nombreuses contributions à une boucle électron-électron dans QED diffusion. L'électron sur le côté gauche du diagramme, représenté par la ligne en trait plein, commence avec quatre élan 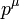 et se termine avec quatre élan
et se termine avec quatre élan 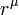 . Il émet un photon valeur virtuelle
. Il émet un photon valeur virtuelle 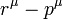 pour transférer l'énergie et de l'élan à l'autre électron. Mais dans ce schéma, avant que cela arrive, il émet un autre photon virtuel transportant quatre élan
pour transférer l'énergie et de l'élan à l'autre électron. Mais dans ce schéma, avant que cela arrive, il émet un autre photon virtuel transportant quatre élan 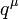 , Et il se résorbe après celui émettant l'autre photon virtuel. L'énergie et la conservation de quantité de mouvement ne déterminent pas les quatre-dynamique
, Et il se résorbe après celui émettant l'autre photon virtuel. L'énergie et la conservation de quantité de mouvement ne déterminent pas les quatre-dynamique 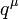 unique, de sorte que toutes les possibilités contribuent également et nous devons intégrer.
unique, de sorte que toutes les possibilités contribuent également et nous devons intégrer.
L'amplitude de ce schéma se retrouve avec entre autres, un facteur de la boucle de
Les diverses 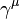 facteurs dans cette expression sont gamma comme matrices pour la formulation de la covariant Équation de Dirac; ils ont à voir avec le spin de l'électron. Les facteurs de
facteurs dans cette expression sont gamma comme matrices pour la formulation de la covariant Équation de Dirac; ils ont à voir avec le spin de l'électron. Les facteurs de  sont la constante de couplage électrique, tandis que le
sont la constante de couplage électrique, tandis que le 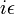 fournir une définition heuristique du contour d'intégration autour des pôles en l'espace de moments. La partie importante pour nos fins est la dépendance
fournir une définition heuristique du contour d'intégration autour des pôles en l'espace de moments. La partie importante pour nos fins est la dépendance 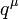 des trois grands facteurs dans l'intégrale, qui sont de la propagateurs de deux lignes d'électrons et la ligne de photons dans la boucle.
des trois grands facteurs dans l'intégrale, qui sont de la propagateurs de deux lignes d'électrons et la ligne de photons dans la boucle.
Cela a une pièce avec deux puissances de 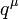 sur le dessus qui domine dans les grandes valeurs de
sur le dessus qui domine dans les grandes valeurs de 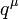 (Pokorski 1987, p 122.):
(Pokorski 1987, p 122.):
Cette intégrale est divergente, et infinie à moins que nous exterminons-le à énergie finie et l'élan d'une certaine façon.
Boucle similaires divergences se produisent dans d'autres théories quantiques des champs.
Renormalisées et les quantités nus
La solution a été de réaliser que les quantités figurant initialement dans les formules de la théorie (comme pour la formule Lagrange), représentant des choses telles que de l'électron de charge électrique et de masse , ainsi que les normalisations du quantique se champs, ne correspondait pas réellement les constantes physiques mesurées en laboratoire. Comme l'a écrit, ils étaient nus quantités qui ne tiennent compte de la contribution des effets de boucle virtuelle particules aux constantes physiques eux-mêmes. Entre autres choses, ces effets seraient inclure la contrepartie quantique de l'arrière-réaction électromagnétique qui tourmenté théoriciens classiques de l'électromagnétisme. En général, ces effets seraient tout aussi divergentes que les amplitudes à l'étude en premier lieu; grandeurs mesurées afin finis seraient en général implique quantités nus divergentes.
Afin de prendre contact avec la réalité, alors, les formules devront être réécrites en termes de quantités mesurables, renormalisées. La charge de l'électron, par exemple, serait définie en termes de quantité mesurée à une spécifique cinématique point de renormalisation ou point de soustraction (qui ont généralement une énergie caractéristique, appelé l'échelle de renormalisation ou simplement échelle d'énergie). Les parties de la gauche au-dessus de Lagrange, impliquant les parties restantes des quantités nus, pourrait alors être réinterprétées comme contretermes, impliqué dans des diagrammes divergents annulation exactement les divergences gênantes pour les autres diagrammes.
Renormalisation dans QED
Par exemple, dans le Lagrange de QED
les champs et constante de couplage sont des quantités vraiment nus, donc l'indice 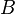 ci-dessus. Classiquement les quantités nus sont écrits de telle sorte que les termes de Lagrange correspondants sont des multiples de ceux renormalisées:
ci-dessus. Classiquement les quantités nus sont écrits de telle sorte que les termes de Lagrange correspondants sont des multiples de ceux renormalisées:
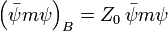
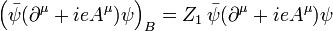
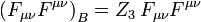 .
.
( Invariance de jauge, via un Identité de Ward-Takahashi, se avère impliquer que nous pouvons renormaliser les deux termes de la pièce dérivée covariante 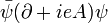 ensemble (Pokorski 1987, p. 115), ce qui est arrivé à
ensemble (Pokorski 1987, p. 115), ce qui est arrivé à  ; il est le même que
; il est le même que 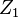 .)
.)
Un terme dans ce lagrangien, par exemple, l'interaction électron-photon illustré à la figure 1, peut alors se écrire
La constante physique  , La charge de l'électron, peut alors être définie en termes de quelque expérience spécifique; nous avons mis l'échelle de renormalisation égal à la caractéristique de l'énergie de cette expérience, et le premier terme donne l'interaction que nous voyons dans le laboratoire (jusqu'à petites corrections finis à partir de diagrammes de boucle, fournir une telle exotica que les corrections d'ordre supérieur à la moment magnétique). Le reste est le contreterme. Si nous sommes chanceux, les parties divergentes de diagrammes de boucles peuvent tous être décomposés en morceaux avec trois jambes ou moins, avec une forme algébrique qui peut être annulé par le second terme (ou par les contretermes similaires qui viennent de
, La charge de l'électron, peut alors être définie en termes de quelque expérience spécifique; nous avons mis l'échelle de renormalisation égal à la caractéristique de l'énergie de cette expérience, et le premier terme donne l'interaction que nous voyons dans le laboratoire (jusqu'à petites corrections finis à partir de diagrammes de boucle, fournir une telle exotica que les corrections d'ordre supérieur à la moment magnétique). Le reste est le contreterme. Si nous sommes chanceux, les parties divergentes de diagrammes de boucles peuvent tous être décomposés en morceaux avec trois jambes ou moins, avec une forme algébrique qui peut être annulé par le second terme (ou par les contretermes similaires qui viennent de 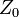 et
et 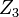 ). Dans CQFD, nous sommes chanceux: la théorie est renormalisable (voir ci-dessous pour plus de détails).
). Dans CQFD, nous sommes chanceux: la théorie est renormalisable (voir ci-dessous pour plus de détails).
Le schéma de la 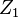 Le sommet de l'interaction contreterme placé comme sur la figure 3 annule l'écart par rapport à la boucle de la figure 2.
Le sommet de l'interaction contreterme placé comme sur la figure 3 annule l'écart par rapport à la boucle de la figure 2.
Le fractionnement des «termes nus" dans les termes et contretermes originaux est venu avant la groupe de renormalisation idées en raison de Kenneth Wilson. Selon le renormalisation des idées du groupe, ce dédoublement est pas naturel et non physique.
Courir constantes
Afin de minimiser la contribution des schémas de boucle à un calcul donné (et donc le rendre plus facile d'extraire des résultats), on choisit un point proche des énergies et moments renormalisation effectivement échangées dans l'interaction. Cependant, le point de renormalisation ne est pas elle-même une quantité physique: les prédictions physiques de la théorie, calculé à toutes les commandes, devraient en principe être indépendant du choix du point de renormalisation, aussi longtemps que ce est dans le domaine d'application de la théorie. Changements d'échelle de renormalisation seront simplement affecter la façon dont beaucoup d'un résultat vient de diagrammes de Feynman sans boucles, et combien provient des restes de pièces finies de diagrammes de boucles. On peut exploiter ce fait pour calculer la variation effective de constantes physiques avec des changements d'échelle. Cette variation est codée par bêta-fonctions, et la théorie générale de ce genre d'échelle dépendance est connu comme le groupe de renormalisation.
Familièrement, les physiciens des particules parlent souvent de certaines constantes physiques comme variant avec l'énergie d'une interaction, mais en fait ce est l'échelle de renormalisation qui est la quantité indépendante. Cette la course ne fournit cependant un moyen commode de décrire les changements dans le comportement d'une théorie de champ sous des changements dans les énergies impliquées dans une interaction. Par exemple, étant donné que la constante de couplage à chromodynamique quantique devient petit à de grandes échelles de l'énergie, la théorie se comporte plus comme une théorie libre comme l'énergie échangée dans une interaction devient grande, un phénomène connu sous le nom liberté asymptotique. Choisir une échelle croissante d'énergie et en utilisant le groupe de renormalisation met bien en évidence à partir de diagrammes de Feynman simples; ont refusé de le faire, la prédiction serait le même, mais découlerait de complexes annulations d'ordre élevé.
Régularisation
Comme la quantité 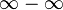 est mal défini, afin de rendre cette notion d'annuler divergences précises, les divergences doivent d'abord être apprivoisé mathématiquement en utilisant la théorie des limites , dans un processus connu sous le nom régularisation.
est mal défini, afin de rendre cette notion d'annuler divergences précises, les divergences doivent d'abord être apprivoisé mathématiquement en utilisant la théorie des limites , dans un processus connu sous le nom régularisation.
Une modification arbitraire essentiellement aux intégrands de boucle ou régulateur, peut rendre les déposer plus rapidement à haute énergie et les quantités de mouvement, de telle sorte que les intégrales convergent. Un régulateur a une échelle d'énergie caractéristique connue sous le nom couper; la prise de ce seuil à l'infini (ou, de manière équivalente, l'échelle de longueur / temps correspondant à zéro) récupère les intégrales d'origine.
Avec le régulateur en place, et une valeur finie pour la coupure, les termes divergents dans les intégrales puis se transforment en termes finis mais coupure dépendant. Après l'annulation de ces termes avec les contributions des contretermes de coupure dépendant, le seuil est prise à l'infini et les résultats physiques finies récupéré. Si la physique sur des échelles que nous pouvons mesurer est indépendante de ce qui se passe à l'échelle de distance et de temps très courts, alors il devrait être possible d'obtenir des résultats de coupure indépendant pour les calculs.
De nombreux types de réglementation différents sont utilisés dans les calculs quantiques de théorie des champs, chacune avec ses avantages et ses inconvénients. Un des plus populaires dans l'usage moderne est régularisation dimensionnelle, inventé par Gerardus 't Hooft et Martinus JG Veltman, qui dompte les intégrales en les transportant dans un espace avec un nombre fractionnaire fictif de dimensions. Une autre est Régularisation Pauli-Villars, qui ajoute particules fictives à la théorie avec de très grandes masses, que ces intégrandes boucle impliquant les particules massives annuler les boucles existantes grand moments.
Pourtant, un autre régime de régularisation est le Lattice régularisation, introduite par Kenneth Wilson, qui prétend que notre espace-temps est construit en réseau hyper-cubique avec la taille fixe de la grille. Cette taille est une coupure naturelle pour la dynamique maximale qu'une particule pourrait posséder lors de la propagation sur le réseau. Et après avoir fait le calcul sur plusieurs réseaux avec différente taille de la grille, le résultat physique est extrapolée à la taille de la grille 0, ou de notre univers naturel. Cela suppose l'existence d'un mise à l'échelle limite.
Une approche mathématique rigoureuse de la théorie de la renormalisation est la soi-disant théorie des perturbations causal, où divergences ultraviolets sont évités dès le départ dans les calculs en effectuant des opérations mathématiques bien définies que dans le cadre de théorie de la distribution. L'inconvénient de la méthode est le fait que l'approche est assez technique et nécessite un haut niveau de connaissances mathématiques.
Régularisation zêta
Julian Schwinger découvert une relation entre zeta régularisation de la fonction et renormalisation, en utilisant la relation asymptotique:
que le régulateur 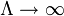 . Sur cette base, il a envisagé d'utiliser les valeurs de
. Sur cette base, il a envisagé d'utiliser les valeurs de 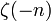 pour obtenir des résultats finis. Même se il a atteint des résultats incohérents, une formule améliorée par Hartle, J. Garcia, E. Elizalde comprend
pour obtenir des résultats finis. Même se il a atteint des résultats incohérents, une formule améliorée par Hartle, J. Garcia, E. Elizalde comprend
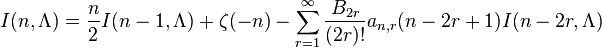 ,
,
où s B 'sont Nombres de Bernoulli et
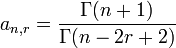 .
.
Ainsi, chaque 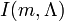 peut se écrire comme une combinaison linéaire de
peut se écrire comme une combinaison linéaire de 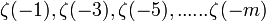
Ou tout simplement à l'aide Formule Abel-Plana nous avons pour chaque intégrale divergente:
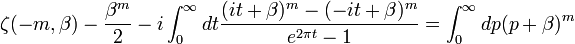 valide lorsque m> 0, Ici, la fonction Zeta est Fonction zeta Hurwitz et Beta est un nombre réel positif.
valide lorsque m> 0, Ici, la fonction Zeta est Fonction zeta Hurwitz et Beta est un nombre réel positif.
L'analogie "géométrique" est donnée par, (si nous utilisons Procédé de rectangle) pour évaluer si l'intégrale:
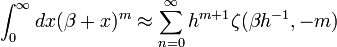
Utilisation Hurwitz régularisation de zeta ainsi que la méthode de rectangle avec l'étape h (à ne pas confondre avec La constante de Planck)
Attitudes et interprétation
Les premiers formulateurs de QED et d'autres théories quantiques des champs étaient, en règle générale, pas satisfait de cet état de choses. Il semblait illégitime de faire quelque chose revient à soustraire de infinis infinis pour obtenir des réponses finis.
Dirac critiques s 'était le plus persistant. Pas plus tard que 1975, il disait:
- La plupart des physiciens sont très satisfaits de la situation. Ils disent: 'électrodynamique quantique est une bonne théorie et nous ne avons pas à vous soucier plus du tout. » Je dois dire que je suis très mécontent de la situation, parce que ce soi-disant «bonne théorie» ne implique négliger infinis qui apparaissent dans ses équations, les négliger de manière arbitraire. Ce est tout simplement pas les mathématiques sensibles. Mathématiques sensibles implique négligent une quantité quand il est petit - pas négliger juste parce qu'il est infiniment grand et vous ne en veulent pas!
Un autre critique importante était Feynman . En dépit de son rôle crucial dans le développement de l'électrodynamique quantique, il écrit ce qui suit en 1985:
- Le jeu de coquille que nous jouons ... est techniquement appelé «renormalisation». Mais peu importe la façon dont le mot d'esprit, ce est encore ce que je appellerais un processus de fofolle! Avoir à recourir à un tel tour de passe-passe nous a empêché de prouver que la théorie de l'électrodynamique quantique est mathématiquement auto-cohérent. Il est surprenant que la théorie n'a pas encore été prouvé auto-cohérent d'une façon ou l'autre maintenant; Je soupçonne que la renormalisation est pas mathématiquement légitime.
Alors que la critique de Dirac a été fondée sur la procédure de renormalisation lui-même, la critique de Feynman était très différent. Feynman a été concerné que toutes les théories des champs connus dans les années 1960 avaient la propriété que les interactions devient infiniment fort à des échelles assez courte distance. Cette propriété, appelée Pôle Landau, fait-il plausible que les théories quantiques des champs étaient incompatibles. En 1974, Gross, Politzer et Wilczek a montré qu'un autre théorie quantique des champs, chromodynamique quantique, n'a pas un pôle landau. Feynman, avec la plupart des autres, admis que QCD est une théorie pleinement compatible.
Le malaise général était presque universelle dans les textes jusqu'à les années 1970 et 1980. Au début des années 1970, cependant, inspiré par le travail sur le groupe de renormalisation et Théorie effective, et malgré le fait que Dirac et plusieurs autres - qui appartenaient tous à la génération plus âgée - jamais retiré leurs critiques, les attitudes ont commencé à changer, surtout chez les jeunes théoriciens. Kenneth G. Wilson et d'autres ont démontré que le groupe de renormalisation est utile dans statistique théorie du champ appliqué au physique de la matière condensée , où il fournit des informations importantes sur le comportement des transitions de phase. En matière condensée, un régulateur à courte distance réelle existe: question cesse d'être continue sur l'échelle de atomes . Divergences courte distance en physique de la matière condensée ne présentent pas un problème philosophique, puisque la théorie de champ ne est une représentation efficace, lissé sur le comportement de la matière de toute façon; il n'y a pas infinis depuis la coupure est en fait toujours finie, et il est parfaitement logique que les quantités sont nus coupure dépendant.
Si QFT détient tout le chemin vers le bas après la Longueur de Planck (où il pourrait céder à la théorie des cordes , causalité théorie des ensembles ou quelque chose de différent), il peut y avoir aucun problème réel avec des divergences à courte distance dans la physique des particules soit; toutes les théories sur le terrain pourrait être simplement théories efficaces sur le terrain. Dans un sens, cette approche fait écho à l'attitude plus que les divergences dans QFT parlent de l'ignorance humaine sur le fonctionnement de la nature, mais reconnaît également que cette ignorance peut être quantifiée et que les théories effectives résultant restent utiles.
Dans QFT, la valeur d'une constante physique, en général, dépend de l'échelle que l'on choisit comme point de renormalisation, et il devient très intéressant d'examiner le groupe de renormalisation fonctionnement de constantes physiques en variation de l'échelle d'énergie. Les constantes de couplage dans le modèle standard de la physique des particules varient de différentes manières avec l'augmentation de l'échelle de l'énergie: le couplage de chromodynamique quantique et le faible couplage isospin de la force électrofaible ont tendance à diminuer, et le faible couplage hypercharge de la force électrofaible tend à augmenter. À l'échelle de l'énergie colossale de 10 15 GeV (bien au-delà de la portée de notre civilisation de accélérateurs de particules), ils deviennent tous à peu près la même taille (Grotz et Klapdor 1990, p. 254), une motivation majeure pour les spéculations sur grande théorie unifiée. Au lieu d'être seulement un problème préoccupant, renormalisation est devenu un outil théorique important pour étudier le comportement des théories sur le terrain dans les différents régimes.
Si une théorie renormalisation avec (par exemple CQFD) ne peut être raisonnablement interprétée comme une théorie de champ effectif, ce est à dire comme une approximation reflétant l'ignorance humaine sur le fonctionnement de la nature, le problème reste de découvrir une théorie plus précise qui n'a pas ces problèmes de renormalisation . Comme Lewis Ryder l'a mis, "Dans la théorie quantique, ces [classiques] divergences ne disparaissent pas;. Au contraire, ils semblent se aggraver Et malgré le succès relatif de la théorie de la renormalisation le sentiment demeure que il devrait y avoir un plus moyen satisfaisant de faire les choses ».
Renormalisabilité
De cette réévaluation philosophique un nouveau concept suit naturellement: la notion de renormalisabilité . Pas toutes les théories se prêtent à la renormalisation de la manière décrite ci-dessus, avec une réserve limitée de contretermes et toutes les quantités deviennent coupure indépendant à la fin du calcul. Si le lagrangien contient combinaisons d'opérateurs de terrain de trop élevée dimension en unités d'énergie, les contretermes nécessaires pour annuler toutes les divergences prolifèrent au nombre infini, et, à première vue, la théorie semble avoir un nombre infini de paramètres libres et donc perdre tout pouvoir prédictif, devenant scientifiquement sans valeur. Ces théories sont appelés non renormalisables.
Le modèle standard de la physique des particules ne contient que des opérateurs renormalisables, mais les interactions de la relativité générale devenir opérateurs non renormalisables si l'on tente de construire une théorie des champs de la gravité quantique de la manière la plus simple, ce qui suggère que la théorie des perturbations est inutile dans l'application de la gravité quantique.
Cependant, dans une théorie de champ effectif, "renormalisabilité" est, à proprement parler, un impropre. Dans une théorie non renormalisables efficace sur le terrain, les termes de la Lagrange ne se multiplient à l'infini, mais avoir des coefficients réprimées par les puissances inverses toujours plus extrêmes de la coupure d'énergie. Si le seuil est un véritable, la quantité, si physique, ce est, la théorie est seulement une description efficace de la physique jusqu'à une certaine énergie maximum ou distance minimale échelle alors ces termes supplémentaires pourraient représenter de véritables interactions physiques. En supposant que les constantes sans dimension dans la théorie ne deviennent trop grandes, les calculs du groupe de boîtes une par des puissances inverses de la coupure, et d'extraire des prévisions approximatives à ordre fini dans la coupure qui ont encore un nombre fini de paramètres libres. Il peut même être utile pour renormaliser ces interactions "non renormalisables".
Interactions non renormalisables dans les théories efficaces sur le terrain deviennent rapidement plus faible que l'échelle d'énergie devient beaucoup plus petite que la coupure. L'exemple classique est le Fermi de la théorie force nucléaire faible, une théorie efficace non renormalisables dont la coupure est comparable à la masse de la Particules W. Ce fait peut également fournir une explication possible de la raison pour laquelle la quasi-totalité des interactions de particules que nous voyons sont descriptibles par les théories renormalisables. Il se peut que d'autres qui peuvent exister à l'échelle de Planck GUT ou deviennent tout simplement trop faible pour détecter dans le domaine, nous pouvons observer, à une exception près: la gravité , dont l'interaction extrêmement faible est amplifié par la présence des masses énormes de étoiles et planètes .
schémas de renormalisation
Dans les calculs réels, les contretermes introduits pour annuler les divergences dans les calculs de diagrammes de Feynman-delà du niveau de l'arbre doit être fixé à l'aide d'un ensemble de conditions de renormalisation. Les régimes de renormalisation communs en usage comprennent:
- Soustraction minimale (MS) et la soustraction régime minimal modifié liés (MS-bar) régime
- Sur-shell système
Application en physique statistique
Comme mentionné dans l'introduction, les méthodes de renormalisation ont été appliquées à la physique statistique, à savoir les problèmes du comportement critique près de second ordre transitions de phase, en particulier au dimensions spatiales fictives juste en dessous du nombre de 4, où le mentionné ci-dessus méthodes pourraient même être affûtées (ie, au lieu de "renormalisabilité" on obtient "super-renormalisabilité"), qui a permis une extrapolation à la dimension spatiale réelle pour les transitions de phase, 3. Détails peut être trouvé dans le livre de Zinn-Justin, mentionné ci-dessous .
Pour la découverte de ces applications inattendues, et de travailler sur les détails, en 1982 le prix Noble de physique a été donné à Kenneth G. Wilson.

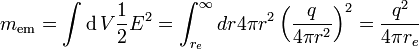
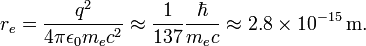
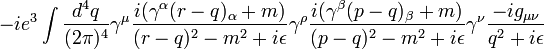
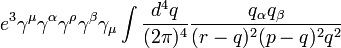
![\ Mathcal {L} = \ bar \ psi_B \ left [i \ gamma_ \ mu (\ partial ^ \ mu + ie_BA_B ^ \ mu) -m_B \ right] \ psi_B - \ frac {1} {4} {B F_ \ mu \ nu} F_B ^ {\ mu \ nu}](../../images/495/49591.png)