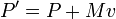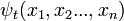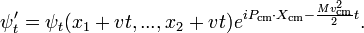Équation de Schrödinger
Contexte des écoles Wikipédia
Cette sélection de wikipedia a été choisi par des bénévoles aidant les enfants SOS de Wikipedia pour cette sélection Wikipedia pour les écoles. Visitez le site Web d'enfants SOS au http://www.soschildren.org/
| Mécanique quantique |
|---|
 Dualité onde-particule |
| Introduction Glossaire · Histoire |
Fond
|
Concepts fondamentaux
|
Expériences
|
Formulations
|
Équations
|
Interprétations
|
Sujets avancés
|
|
Les scientifiques
|
Dans la physique , en particulier la mécanique quantique , l'équation de Schrödinger est une équation qui décrit comment le état quantique d'un système physique change dans le temps. Ce est comme au cœur de la mécanique quantique que les lois de Newton sont à la mécanique classique .
Dans l'interprétation standard de la mécanique quantique, l'état quantique, aussi appelé un vecteur de fonction d'onde ou de l'État, est la description la plus complète qui peut être donné à un système physique. Solutions à l'équation de Schrödinger décrivent des systèmes atomiques et subatomiques, les électrons et les atomes, mais aussi des systèmes macroscopiques, peut-être même l'univers entier. L'équation est nommé d'après Erwin Schrödinger, qui l'a découvert en 1926.
L'équation de Schrödinger peut être mathématiquement transformée en Heisenberg mécanique des matrices, et dans le Intégrale de chemin de Feynman. L'équation de Schrödinger décrit le temps d'une manière qui ne est pas pratique pour les théories relativistes, un problème qui est moins sévère dans la formulation de Heisenberg et complètement absent dans le chemin intégrante.
L'équation de Schrödinger
Il existe plusieurs équations de Schrödinger.
Système quantique général
Pour un système quantique générale:
où
-
 est le fonction d'onde, qui est le probabilité d'amplitude différente pour configurations.
est le fonction d'onde, qui est le probabilité d'amplitude différente pour configurations.  est Plus constante de Planck
est Plus constante de Planck 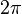 Et il peut être réglé à une valeur de 1 pour l'utilisation de unités naturelles.
Et il peut être réglé à une valeur de 1 pour l'utilisation de unités naturelles. 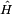 est le Hamiltonien opérateur.
est le Hamiltonien opérateur.
Seule particule en trois dimensions
Pour une seule particule en trois dimensions:
où
 est la fonction d'onde, qui est l'amplitude de la particule d'avoir une position donnée à un moment donné.
est la fonction d'onde, qui est l'amplitude de la particule d'avoir une position donnée à un moment donné.  est la masse de la particule.
est la masse de la particule. 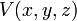 est l'énergie potentielle de la particule a à chaque position.
est l'énergie potentielle de la particule a à chaque position.
Historique et le développement
Einstein interprété Planck quanta s »comme photons , des particules de lumière, et a proposé que l'énergie d'un photon est proportionnelle à sa fréquence, un mystérieux dualité onde-particule . Puisque l'énergie et l'élan sont liés de la même manière que la fréquence et nombre d'onde en la relativité, il se ensuit que l'élan d'un photon est proportionnelle à son nombre d'onde.
DeBroglie émis l'hypothèse que cela est vrai pour toutes les particules, pour des électrons ainsi que des photons, que l'énergie et l'élan d'un électron sont la fréquence et nombre d'onde d'une onde. En supposant que les ondes se propagent à peu près le long des chemins classiques, il a montré qu'ils forment ondes stationnaires seulement pour certaines fréquences discrètes, les niveaux d'énergie discrets qui reproduisaient la ancienne condition quantique.
Suite à ces idées, Schrödinger a décidé de trouver une équation d'onde appropriée pour l'électron. Il a été guidé par L'analogie de Hamilton entre la mécanique et de l'optique, codé dans l'observation que la limite zéro longueur d'onde de l'optique ressemble à un système mécanique --- les trajectoires des rayons lumineux deviennent pointus pistes qui obéissent à un principe de moindre action. Hamilton croit que la mécanique était la limite zéro longueur d'onde de propagation des ondes, mais ne ont pas formuler une équation pour les vagues. Ce est ce que Schrödinger a fait, et une version moderne de son raisonnement est reproduit dans la section suivante. L'équation est qu'il a trouvé (en unités naturelles):
En utilisant cette équation, Schrödinger a calculé le raies spectrales de l'hydrogène par le traitement d'un hydrogène seul atome de négativement chargée électrons comme une vague, 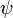 , Se déplaçant dans un puits de potentiel, V, créée par la charge positive des protons . Ce calcul a reproduit les niveaux de l'énergie Modèle de Bohr.
, Se déplaçant dans un puits de potentiel, V, créée par la charge positive des protons . Ce calcul a reproduit les niveaux de l'énergie Modèle de Bohr.
Mais ce ne était pas assez, depuis Sommerfeld avait déjà apparemment reproduit correctement corrections relativistes. Schrödinger utilisé la relation dynamique de l'énergie relativiste de trouver ce qui est maintenant connu sous le nom Équation de Klein-Gordon dans un potentiel de Coulomb :
Il a trouvé les-ondes stationnaires de cette équation relativiste, mais les corrections relativistes en désaccord avec la formule de Sommerfeld. Découragé, il rangea ses calculs et se est retiré dans un chalet de montagne isolé avec un amant.
Tandis que là, Schrödinger a décidé que les calculs non relativistes antérieures étaient assez roman de publier, et a décidé de laisser tomber le problème des corrections relativistes pour l'avenir. Il a réuni son équation d'onde et de l'analyse spectrale de l'hydrogène dans un document en 1926 .. Le document a été approuvé avec enthousiasme par Einstein, qui a vu les matières ondes que l'antidote visualisable à ce qu'il considérait être la trop formelle mécanique des matrices.
L'équation de Schrödinger vous indique le comportement des  , Mais ne dit pas ce que
, Mais ne dit pas ce que  est. Schrödinger a tenté en vain, dans son quatrième article, de l'interpréter comme une densité de charge. En 1926, Max Born, quelques jours après la quatrième et dernier article de Schrödinger a été publié, interprété avec succès
est. Schrödinger a tenté en vain, dans son quatrième article, de l'interpréter comme une densité de charge. En 1926, Max Born, quelques jours après la quatrième et dernier article de Schrödinger a été publié, interprété avec succès  comme une amplitude de probabilité. Schrödinger, cependant, toujours opposé une statistique ou probabiliste approche, avec son associé discontinuités; comme Einstein, qui croyaient que la mécanique quantique était une approximation statistique à une théorie déterministe sous-jacente, Schrödinger n'a jamais été réconciliés avec la Interprétation de Copenhague.
comme une amplitude de probabilité. Schrödinger, cependant, toujours opposé une statistique ou probabiliste approche, avec son associé discontinuités; comme Einstein, qui croyaient que la mécanique quantique était une approximation statistique à une théorie déterministe sous-jacente, Schrödinger n'a jamais été réconciliés avec la Interprétation de Copenhague.
Dérivation
Dérivation heuristique court
Hypothèses
- (1) Le total de l'énergie E d'une particule est
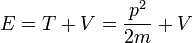
- Ce est l'expression classique pour une particule de masse m dans laquelle l'énergie totale E est la somme de l' énergie cinétique ,
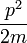 , Et le énergie potentielle V. La dynamique de la particule est p, ou fois la masse de vitesse. L'énergie potentielle est supposée varie avec la position, et peut-être temps aussi.
, Et le énergie potentielle V. La dynamique de la particule est p, ou fois la masse de vitesse. L'énergie potentielle est supposée varie avec la position, et peut-être temps aussi.
- Ce est l'expression classique pour une particule de masse m dans laquelle l'énergie totale E est la somme de l' énergie cinétique ,
- Notez que l'énergie E et l'élan p apparaissent dans les deux relations suivantes:
- (2) Quanta de lumière l'hypothèse d'Einstein de 1905, qui affirme que l'énergie E d'un photon est proportionnelle à la fréquence f de l'onde électromagnétique correspondante:
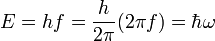
- où le de la fréquence f quanta de rayonnement (photons) sont liés par constante de Planck h,
- et
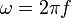 est le pulsation de l'onde.
est le pulsation de l'onde.
- (3) Le de Broglie hypothèse de 1924, qui stipule que toute particule peut être associée à une vague, représentée mathématiquement par une fonction d'onde Ψ de, et que la quantité de mouvement p de la particule est liée à la longueur d'onde λ de l'onde associée par:
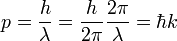
- où
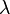 est le longueur d'onde et
est le longueur d'onde et 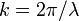 est le nombre d'onde de l'onde.
est le nombre d'onde de l'onde.
- où
Exprimant p et k comme vecteurs , nous avons
Exprimant la fonction d'onde d'une onde de plan complexe
Grande perspicacité de Schrödinger, à la fin de 1925, était d'exprimer la phase d'un onde plane comme un complexe facteur de phase:
- où
- et
et à réaliser que depuis
puis
et de façon similaire à partir du:
puis
et par conséquent:
de sorte que, à nouveau pour une onde plane, il a obtenu:
Et en insérant ces expressions pour l'énergie et l'élan dans la formule classique nous avons commencé avec nous obtenons l'équation de Schrödinger pour célèbre une seule particule dans le cas trois dimensions en présence d'un potentiel V:
Discussion plus
La particule est décrite par une onde, et dans unités naturelles, la fréquence est l'énergie E de la particule, tandis que l'impulsion p est le nombre d'onde k. Ce ne sont pas deux hypothèses distinctes, en raison de la relativité restreinte.
L'énergie totale est la même fonction de l'élan et de la position que dans la mécanique classique:
où le premier terme T (p) est l' énergie cinétique et le second terme V (x) est l'énergie potentielle.
Schrödinger nécessaire qu'un paquet d'ondes à la position x nombre d'onde avec k se déplace le long de la trajectoire déterminée par les lois de Newton dans la limite que la longueur d'onde est petite.
Considérons d'abord le cas sans un potentiel, V = 0.
Alors qu'une onde plane avec l'énergie bonne relation / fréquence obéit à l'équation de Schrodinger libre:
et en additionnant ondes planes, vous pouvez faire une onde arbitraire.
Quand il n'y a pas de potentiel, un paquet d'ondes devrait voyager en ligne droite à la vitesse classique. Le la vitesse v d'un paquet d'ondes est:
qui est l'élan sur la masse comme il se doit. Ce est l'un des Les équations de Hamilton de la mécanique:
après avoir identifié l'énergie et l'élan d'un paquet d'ondes que la fréquence et nombre d'onde.
Pour inclure une énergie potentielle, considérer comme une particule qui se déplace de l'énergie est conservée, de sorte que pour un paquet d'ondes avec un nombre d'onde d'environ k à la position approximative de la quantité x
doit être constante. La fréquence ne change pas comme une onde se déplace, mais le nombre d'onde ne. Alors, où il ya une énergie potentielle, il faut ajouter de la même manière:
Ce est l'équation de schrodinger dépendant du temps. Ce est l'équation pour l'énergie dans la mécanique classique, transformée en une équation différentielle par substitution:
Schrödinger étudié les solutions de ondes stationnaires, puisque ceux-ci étaient les niveaux d'énergie. Les ondes stationnaires ont une dépendance compliquée sur l'espace, mais varient dans le temps d'une manière simple:
substitution, l'équation du temps-dépendant devient l'équation d'onde stationnaire:
Ce est l'équation de Schrödinger indépendante du temps d'origine.
Dans un gradient de potentiel, le k-vecteur d'une vague courte longueur d'onde doit varier de point à point, de garder la constante de l'énergie totale. Feuilles perpendiculaires à la k-vecteur sont les fronts d'onde, et ils changent progressivement la direction, parce que la longueur d'onde ne est pas partout la même. Un paquet d'ondes suit les fronts d'ondes se déplaçant avec la vitesse classique, avec une accélération égale à la force divisée par la masse.
un moyen moderne facile de vérifier que la deuxième loi de Newton est valable pour paquets d'ondes est de prendre le Transformée de Fourier de la équation de Schrödinger dépendante du temps. Pour un potentiel polynôme quelconque cela se appelle l'équation de Schrödinger dans la représentation d'impulsion:
La relation de vitesse de groupe pour le Fourier trasformed paquet d'ondes donne la seconde des équations de Hamilton.
Versions
Il ya plusieurs équations qui vont par le nom de Schrodinger:
Temps équation dépendante
Ce est l'équation du mouvement pour l'état quantique. Dans la forme la plus générale, il est écrit:
Où 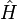 est un opérateur linéaire agissant sur la fonction d'onde
est un opérateur linéaire agissant sur la fonction d'onde  .
. 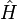 prend en entrée une
prend en entrée une  et produit un autre d'une manière linéaire, une version fonction de l'espace d'une matrice en multipliant un vecteur. Pour le cas spécifique d'une seule particule dans une dimension se déplaçant sous l'influence d'un potentiel V:
et produit un autre d'une manière linéaire, une version fonction de l'espace d'une matrice en multipliant un vecteur. Pour le cas spécifique d'une seule particule dans une dimension se déplaçant sous l'influence d'un potentiel V:
et l'opérateur H peut être lue:
ce est une combinaison de l'opérateur qui tient la dérivée seconde, et l'opérateur qui multiplie ponctuelles  V (x). Lorsqu'il se prononce sur
V (x). Lorsqu'il se prononce sur  il reproduit le côté droit.
il reproduit le côté droit.
Pour une particule en trois dimensions, la seule différence est plus dérivés:
et pour N particules, la différence est que la fonction d'onde est dans l'espace de configuration 3N dimensions, l'espace de toutes les positions possibles des particules.
Cette dernière équation se trouve dans une dimension très élevé, de sorte que les solutions ne sont pas faciles à visualiser.
Temps indépendant équation
Ce est l'équation pour les ondes stationnaires, la valeur propre équation pour H. sous forme de résumé, pour un système quantique générale, il est écrit:
Pour une particule dans une dimension, avec la masse absorbée dans rééchelonnement soit temps ou l'espace:
Mais il existe une restriction supplémentaire --- la solution ne doit pas se développer à l'infini, de sorte qu'il a une norme finie:
Par exemple, lorsqu'il n'y a pas de potentiel, l'équation se lit:
qui a des solutions oscillatoires pour E> 0 (les C sont des constantes arbitraires de):
et des solutions exponentielles pour E <0
Les solutions en croissance exponentielle ont une norme infinie, et ne sont pas physiques. Ils ne sont pas autorisés dans un volume fini avec des conditions aux limites périodiques ou fixes.
Pour un potentiel constant V est la solution oscillatoire E> V et exponentielle E
États propres de l'énergie
Une solution 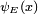 du temps équation indépendante est appelé un état propre de l'énergie avec l'énergie E:
du temps équation indépendante est appelé un état propre de l'énergie avec l'énergie E:
Pour trouver la dépendance temporelle de l'état, envisager de commencer l'équation du temps-dépendante avec une condition initiale 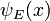 . Dérivé de temps à t = 0 partout est proportionnel à la valeur:
. Dérivé de temps à t = 0 partout est proportionnel à la valeur:
Alors que dans un premier toute la fonction obtient juste redimensionné, et il maintient la propriété que sa dérivée de temps est proportionnelle à lui-même. Donc, pour tous les temps,
substitution,
Alors que la solution de l'équation dépendante du temps avec cette condition initiale est:
ou, avec explicite  s.
s.
Ce est un rappel du fait que les solutions de l'équation indépendante du temps sont les solutions d'ondes stationnaires de l'équation en fonction du temps. Ils ne se multipliés par une phase que le temps passe, et autrement sont inchangées.
Superpositions d'états propres d'énergie changent leurs propriétés en fonction des phases relatives entre les niveaux d'énergie.
Propriétés
Premier Ordre dans le temps
L'équation de Schrödinger décrit l'évolution temporelle d'un état quantique, et doit déterminer la valeur future de la valeur actuelle. Une équation de champ classique peut être second ordre dans les dérivés de temps, l'état classique peut comprendre la dérivée temporelle du champ. Mais un état quantique est une description complète d'un système, de sorte que l'équation de Schrödinger est toujours premier ordre dans le temps.
Linéaire
L'équation de Schrödinger est linéaire dans la fonction d'onde: si 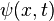 et
et 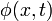 sont des solutions à l'équation en fonction du temps, alors il en est
sont des solutions à l'équation en fonction du temps, alors il en est 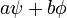 , Où a et b sont des nombres complexes .
, Où a et b sont des nombres complexes .
En mécanique quantique, l'évolution temporelle d'un état quantique est toujours linéaire, pour raisons fondamentales. Bien qu'il existe versions non linéaires de l'équation de Schrödinger, ce ne sont pas des équations qui décrivent l'évolution d'un état quantique, mais équations de champ classiques comme les équations de Maxwell ou la Équation de Klein-Gordon.
L'équation de Schrödinger lui-même peut être considéré comme l'équation du mouvement pour un champ classique pas une fonction d'onde, et en prenant ce point de vue, il décrit une onde cohérente de la matière non relativiste, une vague d'un Bose ou d'un condensat superfluide avec un grand nombre indéfini de particules et d'une phase et une amplitude déterminée.
Véritables états propres
L'équation indépendante du temps est aussi linéaire, mais dans ce cas linéarité a une signification légèrement différente. Si deux fonctions d'onde 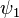 et
et 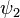 sont des solutions à l'équation indépendante du temps avec la même énergie E, puis une combinaison linéaire des deux est une solution avec une énergie E. Deux solutions différentes avec la même énergie sont appelés dégénérée.
sont des solutions à l'équation indépendante du temps avec la même énergie E, puis une combinaison linéaire des deux est une solution avec une énergie E. Deux solutions différentes avec la même énergie sont appelés dégénérée.
Dans un potentiel arbitraire, il existe une dégénérescence évidente: si une fonction d'onde  résout l'équation indépendante du temps, le fait de
résout l'équation indépendante du temps, le fait de 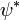 . En prenant des combinaisons linéaires, la partie réelle et imaginaire de
. En prenant des combinaisons linéaires, la partie réelle et imaginaire de  sont chacun des solutions. Alors que la restriction de l'attention sur des fonctions d'onde réelle valeur ne affecte pas le problème de valeur propre indépendante du temps.
sont chacun des solutions. Alors que la restriction de l'attention sur des fonctions d'onde réelle valeur ne affecte pas le problème de valeur propre indépendante du temps.
Dans l'équation dépendante du temps, des ondes conjuguées complexes se déplacent dans des directions opposées. Etant donné une solution de l'équation dépendante du temps 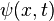 , Le remplacement:
, Le remplacement:
produit une autre solution, et est l'extension de la conjugaison complexe de symétrie le cas en fonction du temps. La symétrie de la conjugaison complexe est appelé retournement temporel.
Temps unitaire Evolution
L'équation de Schrôdinger est unitaire, ce qui signifie que la norme total de la fonction d'onde, la somme des carrés de la valeur à tous les points:
a zéro dérivé de temps.
Le dérivé de 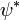 est selon les équations complexes conjugués
est selon les équations complexes conjugués
où l'opérateur 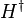 est défini comme le analogique continue de la Conjugué hermitien,
est défini comme le analogique continue de la Conjugué hermitien,
Pour une base discrète, cela signifie simplement que les éléments de matrice de l'opérateur linéaire H obéir:
Le dérivé du produit scalaire est le suivant:
et est proportionnelle à la partie imaginaire de H. Si H n'a pas de partie imaginaire, se il se agit auto-adjoint, alors la probabilité est conservée. Ce est vrai non seulement pour l'équation de Schrödinger comme écrit, mais pour l'équation de Schrödinger non local avec saut:
tant que:
le choix particulier:
reproduit le saut locale dans l'équation de Schrödinger ordinaire. Sur un réseau approximation discrète à un espace continu, H (x, y) a une forme simple:
chaque fois que x et y sont voisins les plus proches. Sur la diagonale
où n est le nombre de voisins les plus proches.
Énergies positives
Les solutions de l'équation de Schrôdinger à un potentiel qui est limitée vers le bas ont une fréquence qui est limitée vers le bas. Pour ne importe quel opérateur linéaire  , Le plus petit vecteur propre minimise la quantité:
, Le plus petit vecteur propre minimise la quantité:
sur tout  qui sont normalisées:
qui sont normalisées:
par le principe de variation.
La valeur de l'énergie pour le Schrôdinger hamiltonien est alors la valeur minimale de:
après une intégration par parties, et le côté de la main droite est positif lorsque précises V est positif.
Définie positive non dégénérée État Rez
Pour potentiels qui sont délimités ci-dessous et ne sont pas infinies sur une région, il ya un état fondamental qui minimise l'intégrale ci-dessus. Cette fonction d'onde de plus basse énergie est réelle et définie positive.
Supposons contradiction qui  est un état d'énergie plus faible et a un changement de signe, puis
est un état d'énergie plus faible et a un changement de signe, puis 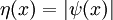 , La valeur absolue de
, La valeur absolue de  obéit
obéit
partout, et
sauf pour un ensemble de mesure nulle. Si 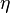 est également un minimimum de l'intégrale, et elle a la même valeur que
est également un minimimum de l'intégrale, et elle a la même valeur que  . Mais en lissant les coudes au changement de signe, la contribution gradient à l'intégrale est réduite alors que l'énergie potentielle est à peine modifié, donc l'énergie de
. Mais en lissant les coudes au changement de signe, la contribution gradient à l'intégrale est réduite alors que l'énergie potentielle est à peine modifié, donc l'énergie de 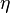 peut être réduite, ce qui est une contradiction.
peut être réduite, ce qui est une contradiction.
L'absence de changements de signe prouve également que l'état du sol est non dégénérée, car se il y avait deux états fondamentaux avec l'énergie E qui ne étaient pas proportionnelle à l'autre, une combinaison linéaire des deux serait également un état fondamental avec un zéro.
Ces propriétés permettent le prolongement analytique de l'équation de Schrôdinger pour être identifié comme un processus stochastique, qui peut être représentée par une intégrale de chemin.
État complet
Les états propres de l'énergie constituent une base --- toute fonction d'onde peut être écrit comme une somme sur les états d'énergie discrets ou une intégrale sur des états d'énergie en continu, ou plus généralement comme une intégrale sur une mesure. Ceci est le théorème spectral en mathématiques, et dans un espace d'état fini ce est juste une déclaration de l'intégralité des vecteurs propres d'une matrice hermitienne.
Conservation locale de probabilité
La densité de probabilité d'une particule est  . Le flux de probabilité est définie comme suit:
. Le flux de probabilité est définie comme suit:
en unités de (probabilité) / (surface x temps).
Le flux de probabilité satisfait à la équation de continuité:
où 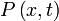 est le densité de probabilité et mesuré en unités de (probabilité) / (volume) = r -3. Cette équation est l'équivalent mathématique de la probabilité loi de conservation.
est le densité de probabilité et mesuré en unités de (probabilité) / (volume) = r -3. Cette équation est l'équivalent mathématique de la probabilité loi de conservation.
Pour une onde plane:
Donc, ce ne est pas seulement la probabilité de trouver la particule la même partout, mais le flux de probabilité est comme prévu à partir d'un objet se déplaçant à la vitesse classique 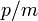 .
.
La raison pour laquelle l'équation de Schrödinger admet un flux de probabilité est parce que tout le saut est local et transmettre en temps.
Heisenberg observables
Il existe de nombreux opérateurs linéaires agissant sur la fonction d'onde, chacune définit une matrice de Heisenberg lorsque les états propres d'énergie sont discrètes. Pour une particule unique, l'opérateur qui tient la dérivée de la fonction d'onde dans une certaine direction:
Est appelé l'opérateur moment. Multipliant les opérateurs est comme matrices de multiplication, le produit de A et B agissant sur  est un acteur sur la sortie de B agit sur
est un acteur sur la sortie de B agit sur  .
.
Un état propre de p obéit à l'équation:
pour un certain nombre k, et pour une fonction d'onde normalisables cette limite k pour être vrai, et l'état propre de l'élan est une onde avec une fréquence k.
L'opérateur de la position x multiplie chaque valeur de la fonction d'onde à la position x par x:
Alors que, pour être un état propre de x, une fonction d'onde doit être entièrement concentrée en un point:
En termes de p, l'hamiltonien est:
Il est facile de vérifier que p agissant sur x agissant sur psi:
tout en agissant sur x p agissant sur psi ne reproduit que le premier terme:
de sorte que la différence des deux ne est pas nul:
ou en termes d'opérateurs:
depuis la dérivée temporelle d'un état est:
tandis que le conjugué complexe est
La dérivée temporelle d'un élément de matrice
obéit à l'équation du mouvement d'Heisenberg. Ceci établit l'équivalence des formalismes Schrodinger et Heisenberg, en ignorant les subtilités mathématiques de la procédure limitant espace continu.
principe de correspondance
L'équation de Schrödinger satisfait la principe de correspondance. Dans la limite de petits paquets d'ondes de longueur d'onde, il reproduit les lois de Newton. Ce est facile de voir de l'équivalence à la mécanique de la matrice.
Tous les opérateurs dans le formalisme de Heisenberg obéissent l'analogue quantique des équations de Hamilton:
Alors que, en particulier, les équations du mouvement pour les opérateurs X et P sont:
dans le Schrodinger image, l'interprétation de cette équation, ce est qu'il donne le taux de temps de changement de l'élément de matrice entre deux états lorsque les Etats changent avec le temps. Prenant la valeur moyenne dans tout état montre que les lois de Newton détiennent non seulement en moyenne, mais exactement, pour les quantités:
Relativité
L'équation de Schrödinger ne tient pas compte des relativistes effets, comme une équation d'onde, elle est invariante sous une Transformation de Galilée, mais pas en vertu d'un Transformation de Lorentz. Mais afin d'y inclure la relativité, l'image physique doit être modifié de façon radicale.
Une généralisation naïve de l'équation de Schrödinger utilise la relation masse-énergie relativiste (en unités naturelles):
pour produire l'équation différentielle:
qui est invariant relativiste, mais second ordre en  Et ne peut donc pas être une équation pour l'état quantique. Cette équation a aussi la propriété qu'il existe des solutions à la fois la fréquence positif et négatif, une solution d'onde plane obéit:
Et ne peut donc pas être une équation pour l'état quantique. Cette équation a aussi la propriété qu'il existe des solutions à la fois la fréquence positif et négatif, une solution d'onde plane obéit:
qui a deux solutions, l'une avec l'autre fréquence positive avec une fréquence négative. Ce est un désastre pour la mécanique quantique, car cela signifie que l'énergie est sans limite ci-dessous.
Une tentative plus sophistiquée pour résoudre ce problème utilise une équation d'onde de premier ordre, le Équation de Dirac, mais encore une fois il ya des solutions d'énergie négative. Afin de résoudre ce problème, il est essentiel d'aller à une image multiparticulaire, et de considérer les équations d'ondes que les équations du mouvement pour un champ quantique, pas pour une fonction d'onde.
La raison en est que la relativité est incompatible avec une seule image de particules. Une particule relativiste ne peut être localisée à une petite région sans que le nombre de particules de devenir indéterminée. Quand une particule est localisée dans une boîte de longueur L, l'élan est incertain d'un montant à peu près proportionnelle à h / L par la principe d'incertitude. Cela conduit à une incertitude d'énergie de hc / L, lorsque | p | est assez grand pour que la masse de la particule peut être négligé. Cette incertitude dans l'énergie est égale à la masse-énergie de la particule quand
et ce est ce qu'on appelle la Longueur d'onde de Compton. En dessous de cette longueur, il est impossible de localiser une particule et être sûr qu'il reste une seule particule, étant donné l'incertitude de l'énergie est suffisamment grande pour produire plus de particules du vide par le même mécanisme qui localise la particule d'origine.
Mais il ya une autre approche de la mécanique quantique relativiste qui ne vous permettent de suivre les chemins de particules simples, et il a été découvert dans le -chemin intégrante formulation. Si les chemins d'intégration dans l'intégrale de chemin comprennent chemins qui se déplacent à la fois avant et en arrière dans le temps en fonction de leur propre bon moment, il est possible de construire une fonction d'onde de fréquence purement positif pour une particule relativiste. Cette construction est attrayant, car l'équation du mouvement pour la fonction d'onde est exactement l'équation d'onde relativiste, mais avec une contrainte non local qui sépare les solutions de fréquence positifs et négatifs. Les solutions de fréquence positives voyagent avant dans le temps, les solutions négatives de fréquence voyagent vers l'arrière dans le temps. De cette façon, ils continuent à la fois analytiquement une fonction champ de corrélation statistique, qui est également représenté par une somme sur des chemins. Mais dans l'espace réel, ils sont les amplitudes de probabilité pour une particule de voyager entre deux points, et peut être utilisé pour générer de l'interaction de particules dans un point de fractionnement et le cadre joindre. Le point de particule relativiste de vue est dû à Richard Feynman.
La méthode de Feynman construit aussi la théorie des champs quantifiés, mais d'un point de vue de la particule. Dans cette théorie, les équations du mouvement pour le domaine peuvent être interprétés comme les équations du mouvement pour une fonction d'onde avec prudence --- la fonction d'onde ne est défini à l'échelle mondiale, et en quelque sorte lié au temps propre de la particule. La notion d'une particule localisée est également délicate --- une particule localisée dans le chemin de particules relativistes correspond intégrés à l'état produit quand un opérateur de champ local agit sur le vide, et exacly quel état est produite dépend du choix des variables de terrain.
Solutions
Certaines techniques générales sont:
- Théorie des perturbations
- Le principe variationnel
- Quantum méthodes de Monte Carlo
- théorie de la fonctionnelle de la densité
- Le Approximation WKB et l'expansion semi-classique
Dans certains cas particuliers, des méthodes spéciales peuvent être utilisées:
- Liste des systèmes mécaniques quantiques avec des solutions analytiques
- Méthode Hartree-Fock et méthodes de post Hartree-Fock
- Discret delta potentiel méthode
Équation de Schrödinger gratuit
Lorsque le potentiel est nul, l'équation de Schrödinger est linéaire à coefficients constants:
où  a été mis à 1. La solution
a été mis à 1. La solution 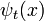 pour toute condition initiale
pour toute condition initiale 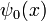 peut être trouvée par transformées de Fourier. Parce que les coefficients sont constants, une onde plane initiale:
peut être trouvée par transformées de Fourier. Parce que les coefficients sont constants, une onde plane initiale:
reste une onde plane. Seuls les changements de coefficients. La substitution:
Alors que A est également oscille dans le temps:
et la solution est la suivante:
Où  , Un retraitement des relations de DeBroglie.
, Un retraitement des relations de DeBroglie.
Pour trouver la solution générale, écrire la condition initiale comme une somme d'ondes planes en prenant sa transformée de Fourier:
L'équation est linéaire, de sorte que chaque ondes planes évolue indépendamment:
Quelle est la solution générale. Lorsque complété par un méthode efficace pour prendre des transformées de Fourier, il devient un algorithme efficace pour trouver la fonction d'onde à tout moment avenir --- transformée de Fourier les conditions initiales, multipliez par une phase, et de transformer le dos.
Gaussien paquet d'ondes
Un exemple simple et instructif est le paquet d'ondes gaussien:
où a est un nombre réel positif, le carré de la largeur de la paquet d'ondes. La normalisation totale de cette fonction d'onde est:
La transformée de Fourier est une gaussienne de nouveau en termes de nombre d'onde k:
Avec la convention de la physique qui met les facteurs de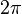 transformées de Fourier dans la k-mesure.
transformées de Fourier dans la k-mesure.
Chaque onde distincte seule phase-rotation dans le temps, de sorte que la solution de temps dépendant de la transformée de Fourier est:
La transformée de Fourier inverse est encore une gaussienne, mais le paramètre a est devenu complexe, et il est un facteur de normalisation globale.
La branche de la racine carrée est déterminée par la continuité dans le temps --- il est la valeur qui est la plus proche de la racine carrée positive d'un. Il est commode de modifier l'échelle de temps pour absorber m, en remplaçant t / m en t.
L'intégrale de  plus tout l'espace est invariant, car il est le produit interne de
plus tout l'espace est invariant, car il est le produit interne de  l'état d'énergie zéro, ce qui est une onde de longueur d'onde infinie, une fonction constante de l'espace. Pour tout Etat de l'énergie, avec fonction d'onde
l'état d'énergie zéro, ce qui est une onde de longueur d'onde infinie, une fonction constante de l'espace. Pour tout Etat de l'énergie, avec fonction d'onde 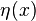 , le produit intérieur:
, le produit intérieur:
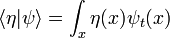 ,
,
seuls les changements dans le temps d'une manière simple: sa phase tourne avec une fréquence déterminée par l'énergie de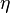 . Quand
. Quand 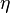 l'énergie a zéro, comme la vague de longueur d'onde infinie, elle ne change pas du tout.
l'énergie a zéro, comme la vague de longueur d'onde infinie, elle ne change pas du tout.
La somme du carré absolu de  est également invariant, qui est une déclaration de la conservation de la probabilité. Explicitement dans une dimension:
est également invariant, qui est une déclaration de la conservation de la probabilité. Explicitement dans une dimension:
Qui donne la norme:
qui a conservé sa valeur, comme il se doit.
La largeur de la gaussienne est la quantité intéressant, et il peut être lue à partir de la forme de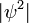 :
:
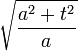 .
.
La largeur finalement croît linéairement dans le temps, comme  . ceci est paquet d'ondes propagation --- peu importe l'étroitesse de la fonction d'onde initiale, une vague Schrodinger finalement remplit tout l'espace. La croissance linéaire est un reflet de l'incertitude de l'élan --- le paquet d'onde est confinée à une bande étroite
. ceci est paquet d'ondes propagation --- peu importe l'étroitesse de la fonction d'onde initiale, une vague Schrodinger finalement remplit tout l'espace. La croissance linéaire est un reflet de l'incertitude de l'élan --- le paquet d'onde est confinée à une bande étroite 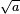 et a donc une dynamique qui est incertaine par la quantité de réciprocité
et a donc une dynamique qui est incertaine par la quantité de réciprocité 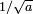 , un écart de vitesse de
, un écart de vitesse de  , et donc dans la position future par
, et donc dans la position future par 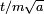 , où le facteur de m a été restaurée en annulant l'rééchelonnement de temps auparavant.
, où le facteur de m a été restaurée en annulant l'rééchelonnement de temps auparavant.
Invariance galiléenne
Boosts galiléens sont des transformations qui se penchent sur le système du point de vue d'un observateur se déplaçant avec un -v de vitesse constante. Un coup de pouce doit modifier les propriétés physiques d'un paquet d'ondes de la même manière que dans la mécanique classique:
Alors que le facteur de phase d'un plan ondes de Schrodinger libre:
est seulement différente dans les coordonnées stimulée par une phase qui dépend de x et t, mais pas à la p.
Une superposition de solutions arbitraire d'ondes planes ayant des valeurs de p est la même superposition d'ondes planes dopé, jusqu'à un ensemble x, t facteur de phase dépendant. Ainsi, toute solution de l'équation de Schrodinger libre, 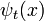 , peut être stimulée dans d'autres solutions:
, peut être stimulée dans d'autres solutions:
Stimuler une fonction d'onde constante produit une onde plane. Plus généralement, le rappel d'une onde plane:
produit une onde stimulé:
Stimuler le paquet d'ondes gaussien propagation:
produit le déplacement gaussien:
Qui se propage de la même façon.
Propagator gratuit
La limite de largeur réduite de la solution de paquet d'ondes gaussien est le propagateur K. Pour les autres équations différentielles, ce qui est parfois appelé la fonction de Green, mais dans la mécanique quantique, il est de tradition de réserver la fonction de nom vert pour la transformée de Fourier de K. Lorsque a est la quantité infinitésimale  , la condition initiale de Gauss, remis à l'échelle de sorte que son intégrale est un:
, la condition initiale de Gauss, remis à l'échelle de sorte que son intégrale est un:
devient unefonction delta, de sorte que son évolution dans le temps:
donne le propagateur.
Notez qu'un paquet d'ondes initial très étroite devient instantanément infiniment large, avec une phase qui est plus rapidement oscillant à de grandes valeurs de x. Cela peut sembler étrange --- la solution passe d'être concentré à un point d'être partout à la fois plus tard, mais il est un reflet de l' incertitude de la dynamique d'une particule localisée. A noter également que la norme de la fonction d'onde est infini, mais cela est également correcte, puisque la place d'une fonction delta est divergente de la même manière.
Le facteur  est une quantité infinitésimale qui est là pour faire en sorte que les intégrales sur K sont bien définis. Dans la limite qui
est une quantité infinitésimale qui est là pour faire en sorte que les intégrales sur K sont bien définis. Dans la limite qui  devient nul, K devient purement oscillatoire et intégrales de K ne sont pas absolument convergente. Dans le reste de cette section, il sera mis à zéro, mais pour toutes les intégrations plus états intermédiaires pour être bien définies, la limite
devient nul, K devient purement oscillatoire et intégrales de K ne sont pas absolument convergente. Dans le reste de cette section, il sera mis à zéro, mais pour toutes les intégrations plus états intermédiaires pour être bien définies, la limite 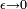 est de seulement être prise après l'état final est calculé.
est de seulement être prise après l'état final est calculé.
Le propagateur est l'amplitude pour atteindre le point x à l'instant t, lors du démarrage à l'origine, x = 0. Par invariance par translation, l'amplitude pour atteindre un point x lors du démarrage au point y est la même fonction, ne traduit:
Dans la limite lorsque t est petit, le propagateur converge vers une fonction delta:
mais seulement dans le sens des distributions. L'intégrale de cette quantité, multipliée par une différentiable arbitraire fonction de test donne la valeur de la fonction de test à zéro. Pour le voir, notons que l'intégrale sur tout l'espace de K est égal à 1 en tout temps:
depuis cette intégrale est l'intérieure-produit de K avec la fonction d'onde uniforme. Mais le facteur de phase dans l'exposant a une dérivée spatiale non nulle partout sauf à l'origine, et donc quand le temps est petit il ya des annulations de phase rapide à tous, mais un point. Cela est rigoureusement vrai quand la limite 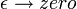 est prise après tout le reste.
est prise après tout le reste.
Ainsi, le noyau de propagation est l'avenir évolution dans le temps d'une fonction delta, et elle est continue dans un sens, elle converge vers la fonction delta initial à petites fois. Si la fonction d'onde initiale est un pic infiniment étroite à la position 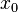 :
:
il devient l'onde oscillatoire:
Étant donné que chaque fonction peut être écrit comme une somme de pointes étroites:
l'évolution temporelle de chaque fonction est déterminée par le noyau de propagation:
Et cela est une autre façon d'exprimer la solution générale. L'interprétation de cette expression est que l'amplitude pour une particule d'être trouvé au point x à l'instant t est l'amplitude qu'il a commencé à 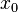 fois l'amplitude qu'il est passé de
fois l'amplitude qu'il est passé de 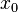 à x, additionnée sur tous les points de départ possibles. En d'autres termes, il est une convolution du noyau K avec la condition initiale.
à x, additionnée sur tous les points de départ possibles. En d'autres termes, il est une convolution du noyau K avec la condition initiale.
Depuis l'amplitude de voyager de x à y, après un temps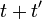 peut être considéré en deux étapes, le propagateur obéit à l'identité:
peut être considéré en deux étapes, le propagateur obéit à l'identité:
Qui peut être interprété comme suit: l'amplitude de voyager de x à z dans le temps t + t 'est la somme de l'amplitude de voyager de x à y dans le temps t multiplié par l'amplitude de voyager de y à z dans le temps t' , additionnée sur tous les états intermédiaires possibles y. Ceci est une propriété d'un système quantique arbitraire, et en divisant le temps en plusieurs parties, elle permet l'évolution dans le temps d'être exprimé en tant que intégrale de chemin.
Continuation analytique Diffusion
La propagation de paquets d'ondes en mécanique quantique est directement liée à la propagation de densités de probabilité dans diffusion.Pour une particule qui est la marche aléatoire, la fonction de densité de probabilité en tout point satisfait l'équation de diffusion:
où le facteur de deux, ce qui peut être éliminé par un temps ou d'espace mise à l'échelle, est seulement pour plus de commodité.
Une solution de cette équation est la gaussienne d'étalement:
et étant donné que l'intégrale de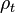 , est constante, tandis que la largeur est de plus étroit à petites fois, cette fonction se rapproche d'une fonction delta à t = 0:
, est constante, tandis que la largeur est de plus étroit à petites fois, cette fonction se rapproche d'une fonction delta à t = 0:
de plus, seulement dans le sens de la distribution, de sorte que
pour toute lissefonction de test f.
La gaussienne d'étalement est le noyau de propagation de l'équation de diffusion et il obéit à l'identité de convolution:
Qui permet la diffusion à exprimer comme un chemin intégrante. Le propagateur est l'exponentielle d'un opérateur H:
qui est l'opérateur de diffusion infinitésimale.
Une matrice a deux indices qui, dans l'espace continu rend une fonction de x et x '. Dans ce cas, en raison de l'invariance par translation, l'élément de matrice K ne dépendent que de la différence de la position, et un abus commode de notation est de se référer à l'opérateur, les éléments de la matrice, et la fonction de la différence par le même nom:
invariance de traduction signifie que la multiplication de matrice continue:
est vraiment convolution:
Le exponentielle peut être définie sur une gamme de t de qui comprennent des valeurs complexes, tant que des intégrales sur le noyau de propagation séjour convergente.
Tant que la partie réelle de z est positif, pour les grandes valeurs de x K est exponentielle en baisse et intégrales sur K sont absolument convergente.
La limite de cette expression pour z venir près de l'axe imaginaire pur est le propagateur Schrodinger:
et cela donne une explication plus conceptuel pour l'évolution temporelle de gaussiennes. De l'identité fondamentale des exponentiation, ou l'intégration de chemin:
détient pour tous z valeurs complexes où les intégrales sont absolument convergente de sorte que les opérateurs sont bien définis.
Alors que l'évolution à partir d'un quantum de Gauss, qui est le noyau K de diffusion:
donne l'état du temps évolué:
Ceci explique la forme de diffusion des solutions de Gauss:
Principe variationnel
Le principe variationnel affirme que pour toute toute hermitienne matrice A, la plus petite valeur propre minimise la quantité:
sur la sphère unité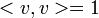 .Ceci fait suite par le procédé demultiplicateurs de Lagrange, au minimum le gradient de la fonction est parallèle à la pente de la contrainte:
.Ceci fait suite par le procédé demultiplicateurs de Lagrange, au minimum le gradient de la fonction est parallèle à la pente de la contrainte:
qui est la condition de valeur propre
de sorte que les valeurs extrêmes d'une forme quadratique A sont les valeurs propres de A, et la valeur de la fonction aux valeurs extrêmes est juste la valeur propre correspondante:
Lorsque la matrice hermitienne est l'hamiltonien, la valeur minimum est le niveau d'énergie le plus bas.
En l'espace de toutes les fonctions d'onde, la sphère unité est l'espace de toutes les fonctions d'onde normalisées , les minimise l'état fondamental
, les minimise l'état fondamental
ou, après une intégration par parties,
Tous les points fixes viennent en paires conjuguées complexes depuis l'intégrale est réel. Comme les points fixes sont des valeurs propres, toute combinaison linéaire est un point fixe, et la partie réelle et imaginaire sont deux points stationnaires.
L'état de plus basse énergie a une fonction d'onde définie positive, parce donné une  qui minimise le, intégrante
qui minimise le, intégrante 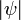 , la valeur absolue est aussi un minimiseur. Mais cette minimiseur a angles vifs à des endroits où
, la valeur absolue est aussi un minimiseur. Mais cette minimiseur a angles vifs à des endroits où  les changements signent, et ces angles vifs peut être complété afin de réduire la contribution gradient.
les changements signent, et ces angles vifs peut être complété afin de réduire la contribution gradient.
Potentiel et jardin État
Pour une particule dans un potentiel définie positive, l'état fondamental fonction d'onde est réel et positif, et a une double interprétation que la densité de probabilité pour un processus de diffusion. L'analogie entre la diffusion et le mouvement quantique non-relativiste, a découvert l'origine et exploitée par Schrodinger, a conduit à de nombreuses solutions exactes.
Une fonction d'onde définie positive:
est une solution de l'équation de Schrôdinger indépendante du temps avec m = 1 et potentiel:
avec zéro énergie totale. W, le logarithme de la fonction d'onde de l'état fondamental. Le second terme est dérivé ordre supérieur dans  , et en ignorant lui donne le rapprochement semi-classique.
, et en ignorant lui donne le rapprochement semi-classique.
La forme de la fonction d'onde de l'état fondamental est motivée par l'observation que la fonction d'onde de l'état fondamental est la probabilité de Boltzmann pour un problème différent, la probabilité de trouver une particule diffusant dans l'espace avec l'énergie libre à différents points donnés par W. Si la diffusion obéit bilan détaillé et la constante de diffusion est partout la même, l' équation de Fokker-Planck pour cette diffusion est l'équation de Schrödinger lorsque le paramètre de temps est autorisé à être imaginaire. Ce prolongement analytique donne les états propres d'une double interprétation --- soit en tant que les niveaux d'énergie d'un système quantique, ou les temps de relaxation pour une équation stochastique.
Oscillateur harmonique
Article détaillé: Oscillateur harmonique quantique.
W doit croître à l'infini, de sorte que la fonction d'onde a une intégrale finie. La forme analytique simple est:
avec une constante arbitraire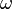 , ce qui donne la possibilité:
, ce qui donne la possibilité:
Ce potentiel décrit unoscillateur harmonique, avec la fonction d'onde de l'état fondamental:
L'énergie totale est égale à zéro, mais le potentiel est décalé par une constante. L'énergie du potentiel d'habitude de l'oscillateur harmonique non décalé de l'état fondamental:
est alors la constante additive:
qui est le point zéro de l'énergie de l'oscillateur.
Potentiel Coulomb
Une autre forme simple mais utile est
où W est proportionnel à la coordonnée radiale. Ceci est l'état du sol pour les deux potentiels différents, en fonction de la dimension. Dans une dimension, le potentiel correspondant est singulier à l'origine, où il a une certaine densité non nulle:
et, jusqu'à un certain changement d'échelle de variables, tel est l'état de plus basse énergie pour un potentiel de fonction delta, avec l'énergie liée à l'état ajouté le.
avec l'énergie de l'état fondamental:
et la fonction d'onde de l'état fondamental:
Dans les dimensions supérieures, la même forme donne la possibilité:
qui peuvent être identifiés comme la loi de Coulomb attrayante, à une constante additif qui est l'énergie de l'état fondamental. Ceci est la superpotentiel qui décrit le niveau d'énergie le plus bas de l'atome d'hydrogène, une fois que la masse est restauré par l'analyse dimensionnelle:
où 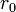 est le Rayon de Bohr, avec l'énergie
est le Rayon de Bohr, avec l'énergie
Le ansatz
modifie le potentiel coulombien d'inclure un terme proportionnel à quadratique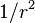 , qui est utile pour le moment cinétique non nul.
, qui est utile pour le moment cinétique non nul.
Formalisme de l'opérateur
Bra-ket Notation
Dans le formulation mathématique de la mécanique quantique, un système physique est entièrement décrite par un vecteur dans un complexe espace de Hilbert, la collecte de toutes les fonctions d'onde normalisables possibles. La fonction d'onde est juste un autre nom pour le vecteur des amplitudes complexes, et seulement dans le cas d'une seule particule dans la représentation de position est-il une vague dans le sens habituel, une vague dans l'espace-temps. Pour les systèmes plus complexes, il est une onde dans un énorme espace de tous les mondes possibles. Deux vecteurs non nuls qui sont des multiples de l'autre, deux fonctions d'onde qui sont les mêmes jusqu'à rééchelonnement, représentent le même état physique.
Le vecteur de fonction d'onde peut être écrit de différentes manières:
- 1. comme un résumévecteur ket:
- 2. Comme une liste de nombres complexes, les composants par rapport à une liste discrète de vecteurs de base normalisables
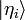 :
: - 3. Comme une superposition continue de vecteurs de base non-normalisables, comme les états de position
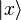 :
:
- 1. comme un résumévecteur ket:
Le fossé entre la base continue et la base discrète peut être comblé en limitant arguments. Les deux peuvent être formellement unifiés par la pensée de chacun comme une mesure sur la ligne de nombre réel.
Dans la notation la plus abstraite, l'équation de Schrödinger est écrit:
qui ne dit que la fonction d'onde évolue linéairement dans le temps, et les noms de l'opérateur linéaire qui donne le dérivé de temps l'hamiltonien H. En termes de la liste discrète de coefficients:
qui réaffirme simplement que l'évolution du temps est linéaire, puisque le hamiltonien agit par multiplication matricielle.
Dans une représentation continue, l'hamiltonien est un opérateur linéaire qui agit par la version continue de la multiplication matricielle:
Prenant le complexe conjugué:
Pour que l'évolution temporelle d'être unitaire, pour préserver les produits scalaires, la dérivée dans le temps du produit intérieur doit être nulle:
pour un état arbitraire 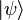 , qui exige que H est hermitique. Dans une représentation discrète, cela signifie que
, qui exige que H est hermitique. Dans une représentation discrète, cela signifie que 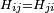 . lorsque h est continue, il devrait être auto-adjoint, qui ajoute une certaine exigence technique H ne mélangez pas les Etats normalisables avec les Etats qui violent les conditions aux limites ou qui sont manifestement unnormalizable.
. lorsque h est continue, il devrait être auto-adjoint, qui ajoute une certaine exigence technique H ne mélangez pas les Etats normalisables avec les Etats qui violent les conditions aux limites ou qui sont manifestement unnormalizable.
La solution formelle de l'équation est l'exponentielle de matrice ( unités naturelles):
Pour chaque opérateur hamiltonien indépendant du temps,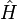 il existe un ensemble d'états quantiques,
il existe un ensemble d'états quantiques,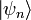 , connu sous le nomdes états propres de l'énergie, et des nombres réels correspondant
, connu sous le nomdes états propres de l'énergie, et des nombres réels correspondant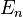 répondant à laéquation aux valeurs propres.
répondant à laéquation aux valeurs propres.
Ceci est l'équation de Schrödinger indépendante du temps.
Pour le cas d'une seule particule, l'hamiltonien est l'opérateur linéaire suivant ( unités naturelles):
qui est un des opérateurs auto-adjoints lorsque V est pas trop singulier et ne pousse pas trop vite. opérateurs auto-adjoints ont la propriété de leurs valeurs propres sont réelles de tout fondement, et leurs vecteurs propres forment un ensemble complet, soit discrète ou continue.
Exprimé dans une base de vecteurs propres de H, l'équation de Schrödinger devient trivial:
Ce qui signifie que chaque état propre de l'énergie est multiplié par une seule phase complexe:
Qui est ce qui signifie matrice exponentiation --- l'évolution temporelle agit pour faire tourner les fonctions propres de H.
Lorsque H est exprimée en tant que matrice pour des fonctions d'onde dans une base de l'énergie discret:
de sorte que:
Les propriétés physiques des C de sont extraites par intérim par les opérateurs, les matrices. En redéfinissant la base de sorte qu'il tourne avec le temps, les matrices deviennent dépendant du temps, qui est la représentation de Heisenberg.
Invariance galiléenne
Symétrie galiléenne exige que H (p) est quadratique en p à la fois dans l'hamiltonien formalisme classique et quantique. Pour boosts galiléennes pour produire un p-indépendante facteur de phase, px - Ht doivent avoir une forme très spéciale --- traductions en p doivent être compensés par un changement dans H. Ceci est vrai que lorsque H est quadratique.
Le générateur infinitésimal de Renforce à la fois le cas classique et quantique est:
où la somme est sur les différentes particules, et B, X, p sont des vecteurs.
Le support de poisson / collecteur de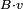 x et p générer boosts infinitésimales, avec v le vecteur vitesse de boost infinitésimale:
x et p générer boosts infinitésimales, avec v le vecteur vitesse de boost infinitésimale:
L'itération de ces relations est simple, car ils ajoutent une quantité constante à chaque étape. Par itération, de la dv incrémentielle résumer à la quantité finie V:
B divisé par la masse totale est le centre actuel de la position de masse moins les moments de temps le centre de la vitesse de masse:
En d'autres termes, B / M est l'estimation courante de la position que le centre de masse dû au temps zéro.
La déclaration que B ne change pas avec le temps est le centre du théorème de masse. Pour un système invariant galiléen, le centre de masse se déplace à une vitesse constante, et l'énergie cinétique totale est la somme de l'énergie cinétique centre de masse et l'énergie cinétique mesuré par rapport au centre de masse.
Depuis B est explicitement dépendante du temps, H ne commute pas avec B, plutôt:
ce qui donne la loi de transformation H sous boosts infinitésimales:
l'interprétation de cette formule est que le changement dans le cadre d'un coup de pouce H infinitésimal est entièrement donnée par le changement du centre de l'énergie cinétique de masse, qui est le produit scalaire de l'impulsion totale avec la vitesse de suralimentation infinitésimale.
Les deux quantités (H, P) forment une représentation du groupe de Galilée avec charge centrale M, où seulement H et P sont des fonctions classiques sur l'espace des phases ou des opérateurs de mécanique quantique, tandis que M est un paramètre. La loi de transformation pour infinitésimale v:
peut être itéré comme précédemment --- P va de P à P + MV par incréments infinitésimaux de v, tandis que H change à chaque étape d'une quantité proportionnelle à P, qui varie linéairement. La valeur finale de H est alors modifiée par la valeur de P à mi-chemin entre la valeur initiale et la valeur de fin:
Les facteurs proportionnels à la charge M centrale sont les phases de fonction d'onde supplémentaires.
Renforce donnent trop d'informations dans le seul cas-particules, depuis symétrie galiléenne détermine complètement le mouvement d'une particule unique. Compte tenu d'une solution dépend du temps multi-particules:
avec un potentiel qui dépend uniquement des positions relatives des particules, il peut être utilisé pour générer la solution stimulé:
Pour le problème de l'onde stationnaire, le mouvement du centre de masse ajoute juste une phase globale. Lors de la résolution pour les niveaux des systèmes de plusieurs particules d'énergie, invariance galiléenne permet au centre du mouvement de masse pour être ignoré.

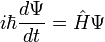
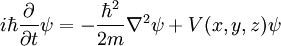
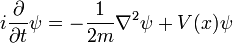
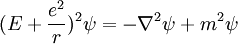
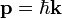
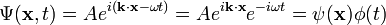


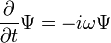
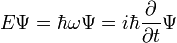
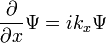
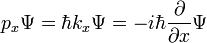
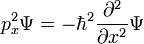
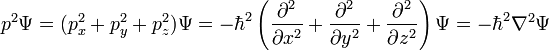
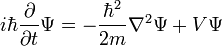

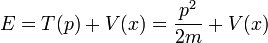
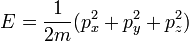
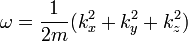
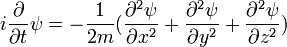
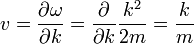
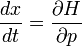
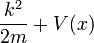
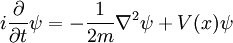
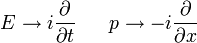
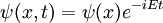
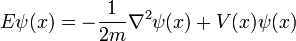

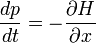
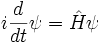
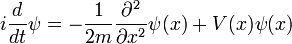
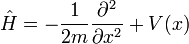
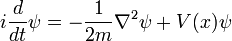
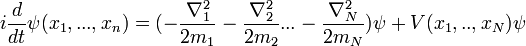
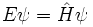
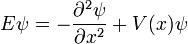

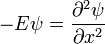
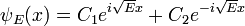
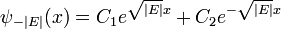
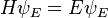
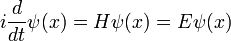
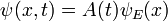
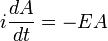

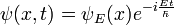
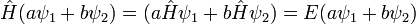
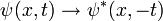

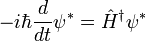
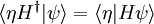

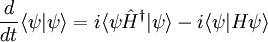
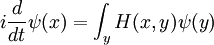
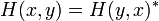
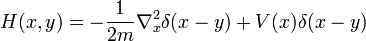
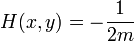
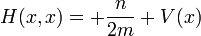
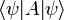
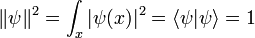
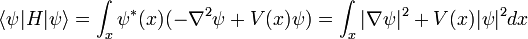
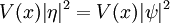
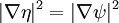
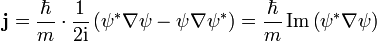
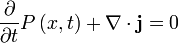
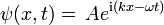
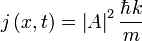
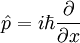
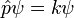
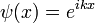
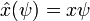
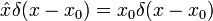
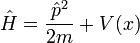
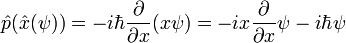
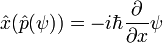
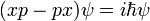
![[X, p] = xp - px = i \ hbar \,](../../images/532/53228.png)
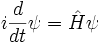
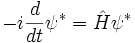
![{D \ over dt} \ langle \ eta | A | \ psi \ rangle = - \ eta \ hat HA \ psi + \ eta AH \ psi = [H, A] \,](../../images/532/53231.png)
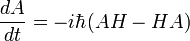


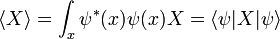
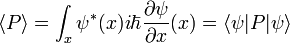
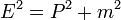
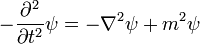
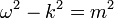
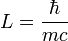
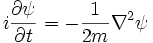
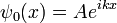
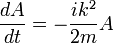
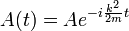
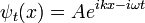
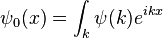
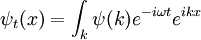
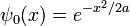
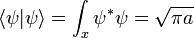
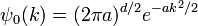

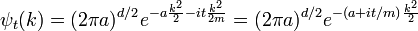
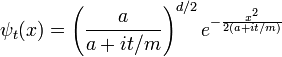
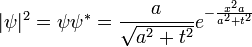
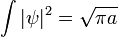
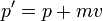
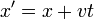
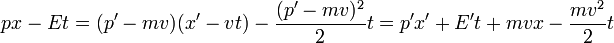

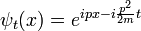
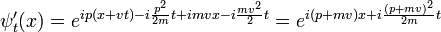
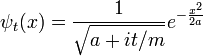
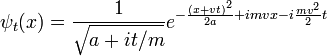
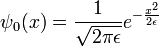
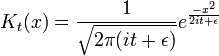
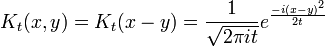
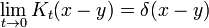
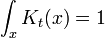
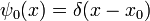
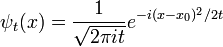
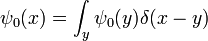

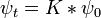
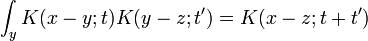
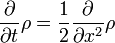
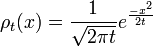
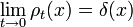
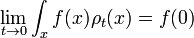
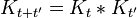
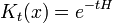
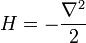
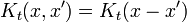
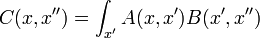
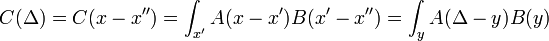
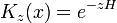
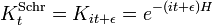


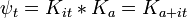
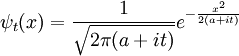
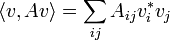
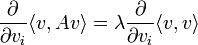
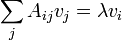
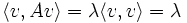
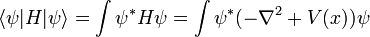

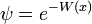


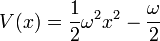
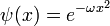
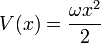
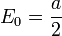
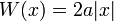
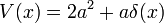
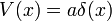
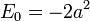
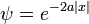
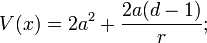
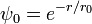
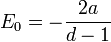
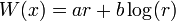
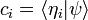

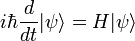

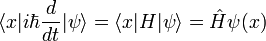
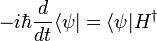

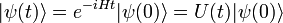
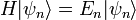
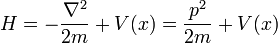
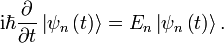

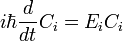
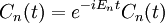

![[B\cdot v ,x_i] = vt
\,](../../images/533/53353.png)
![[B\cdot v ,p_i] = v m_i
\,](../../images/533/53354.png)
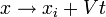
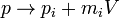
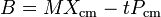
![{dB\over dt} = [H,B] + {\partial B \over \partial t} = 0
\,](../../images/533/53358.png)
![[B\cdot v,H] = - P_\mathrm{cm} v
\,](../../images/533/53359.png)