Número cardinal

Aleph-0, o menor cardinal infinito

Em matemática , os números cardinais, ou cardeais para breve, são uma espécie generalizada de número utilizado para designar o tamanho de um definida, conhecida como o seu cardinalidade. Para conjuntos finitos a cardinalidade é dada por um número natural , sendo simplesmente o número de elementos do conjunto. Há também números cardinais transfinitos para descrever os tamanhos de conjuntos infinitos. Por um lado, um subconjunto apropriado A de um infinito conjunto S pode ter a mesma cardinalidade como S. Por outro lado, talvez também contraintuitivamente, nem todos os conjuntos infinitos têm a mesma cardinalidade. Há uma caracterização formal que explica como alguns conjuntos infinitos têm cardinalities que são estritamente menor do que outros conjuntos infinitos.

Os números cardinais são: . Isto é, eles são os números naturais (cardeais finitos), seguido pela números aleph (cardeais infinitos). Os números aleph são indexados por números ordinais . Os números naturais e números aleph são subclasses dos números ordinais. Se o axioma da escolha falhar, a situação torna-se mais complicado - há cardeais infinitos adicionais que não são alephs.

Conceitos de cardinalidade estão embutidos na maioria dos ramos da matemática e são essenciais para o seu estudo. Cardinality é também uma área estudada por si mesma como parte da teoria dos conjuntos , particularmente na tentativa de descrever as propriedades de grandes cardeais.

História

A noção de cardinalidade, como agora compreendido, foi formulado por Georg Cantor , o criador da teoria dos conjuntos , em 1874-1884.

Cantor estabelecido pela primeira vez cardinalidade como um instrumento para comparar conjuntos finitos; por exemplo, os conjuntos {1,2,3} e {2,3,4} não são iguais, mas tem a mesma cardinalidade, designadamente três.

Cantor identificado o facto um-para-um a correspondência é a maneira de dizer que dois conjuntos têm o mesmo tamanho, chamado "cardinalidade", no caso de conjuntos finitos. Usando essa correspondência de um-para-um, ele aplicou o conceito de conjuntos infinitos; por exemplo, o conjunto de números naturais N = {0, 1, 2, 3, ...}. Ele chamou esses números cardinais números cardinais transfinitos, e definidos com todos os conjuntos de um-para-um correspondência com N a ser (conjuntos infinitos contáveis) numeráveis.

Nomeando este número cardinal 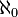, aleph-null, Cantor provou que qualquer subconjunto ilimitado de N tem a mesma cardinalidade como N, mesmo que isso possa parecer, a princípio, contrária à intuição. Ele também provou que o conjunto de todos pares ordenados de números naturais é denumerable (o que implica que o conjunto de todos os números racionais é denumerable), e mais tarde provou que o conjunto de todos números algébricos também é enumerável. Cada número z algébrica pode ser codificado como uma sequência finita dos inteiros que são os coeficientes da equação polinomial dos quais é a solução, isto é, a ordenada n-tuplo em conjunto com um par de racionais de tal modo que z é a raiz do polinómio única com coeficientes que se situa no intervalo .

Em seu artigo de 1874, Cantor provou que não existem números cardinais de ordem superior, mostrando que o conjunto dos números reais tem cardinalidade maior do que a de N. Sua apresentação original usou um argumento complexo com intervalos aninhados, mas em um papel 1891, ele mostrou o mesmo resultado usando sua engenhosa, mas simples argumento diagonal. Este novo número cardinal, chamado de cardinalidade do continuum, foi denominado c por Cantor.

Cantor também desenvolveu uma grande parte da teoria geral dos números cardinais; ele provou que existe um menor número cardinal transfinite ( 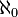, Aleph-null) e que, para cada número cardinal, há uma próxima maior cardeal .

Sua hipótese do contínuo é a proposição de que c é o mesmo que , Mas este tem sido encontrado para ser independente dos axiomas da teoria dos conjuntos padrão matemático; ele pode nem ser provada nem refutada sob as premissas padrão.

Motivação

Em uso informal, um número cardinal é o que é normalmente referido como um número de contagem , desde que 0 é incluído: 0, 1, 2, .... Eles podem ser identificados com os números naturais a partir de 0. Os números de contagem são exatamente o que pode ser definido como o formalmente números cardinais finitos. Cardeais infinitos ocorrem apenas em matemática de nível superior e lógica.

Mais formalmente, um número diferente de zero podem ser usadas para duas finalidades: para descrever o tamanho de um conjunto, ou para descrever a posição de um elemento de uma sequência. Para conjuntos finitos e sequências é fácil ver que essas duas noções coincidem, uma vez que para cada número que descreve uma posição em uma seqüência podemos construir um conjunto que tem exatamente o tamanho certo, por exemplo 3 descreve a posição de 'c' na seqüência <'a', 'b', 'c', 'd', ...>, e nós podemos construir o conjunto {a, b, c}, que tem três elementos. No entanto quando se lida com conjuntos infinitos, é essencial distinguir entre os dois - as duas noções são de fato diferentes para conjuntos infinitos. Considerando o aspecto posição leva a números ordinais, enquanto o aspecto tamanho é generalizado pelos números cardinais descritos aqui.

A intuição por trás da definição formal do cardeal é a construção de uma noção da dimensão relativa ou "grandeza" de um conjunto sem referência ao tipo de membros que ele tem. Para conjuntos finitos isso é fácil; um simplesmente conta o número de elementos de um conjunto tem. A fim de comparar os tamanhos dos conjuntos maiores, é necessário apelar para noções mais sutis.

Um conjunto Y é pelo menos tão grande como ou maior do que ou igual a um conjunto X, se houver um injetivo (um-para-um) mapeamento dos elementos de X para os elementos de Y. Um mapeamento um-para-um identifica cada elemento do conjunto X com um único elemento do conjunto de Y. Isto é mais facilmente compreendido através de um exemplo; suponhamos que tem os conjuntos de X = {1,2,3} e Y = {a, b, c, d}, em seguida, utilizar esta noção de tamanho que se observar que existe um mapeamento:

1 um →

2 b →

3 → c

que é um-para-um, e, por conseguinte, concluir que Y tem cardinalidade maior do que ou igual a x. Observe o elemento d não tem mapeamento de elemento a ele, mas isso é permitido, já que só necessitam de um mapeamento um-para-um, e não necessariamente um one-to-one e para mapeamento. A vantagem deste conceito é que ele pode ser estendido para conjuntos infinitos.

Podemos, então, estender isso para uma relação de estilo igualdade. Dois conjuntos X e Y são referidos como tendo a mesma cardinalidade se existe um bijection entre X e Y. Pelo Schroeder-Bernstein teorema, isto é equivalente a não ser ao mesmo tempo um mapeamento um-para-um de X para Y e um mapeamento um-para-um de Y para X. Nós, então, escrever | X | = | Y |. O número cardinal de si X é muitas vezes definido como o mínimo ordinal um com | a | = | X |. Isso é chamado de von Neumann atribuição cardeal; para esta definição para fazer sentido, deve-se comprovar que cada jogo tem a mesma cardinalidade como alguns ordinal; esta declaração é a princípio bem encomendar. No entanto, é possível discutir a cardinalidade relativa dos conjuntos sem atribuir explicitamente nomes de objetos.

O exemplo clássico é o de utilizar o hotel paradoxo infinito, também chamada O paradoxo de Hilbert do Grand Hotel. Suponha que você é um gerente em um hotel com um número infinito de quartos. O hotel está cheio, e então um novo hóspede chega. É possível encaixar o hóspede extra em perguntando o hóspede que estava na sala 1 para mover para a sala 2, o hóspede do quarto 2 para se deslocar para a sala 3, e assim por diante, deixando espaço 1 vaga. Nós podemos explicitamente escrever um segmento desse mapeamento:

↔ 1 2

2 ↔ 3

3 ↔ 4

...

n ↔ n + 1

...

Desta forma, podemos ver que o conjunto {1,2,3, ...} tem o mesmo cardinality que o jogo {2,3,4, ...} desde uma bijeção entre a primeira ea segunda foi mostrado . Isso motiva a definição de um conjunto infinito ser qualquer conjunto que tem um subconjunto próprio de a mesma cardinalidade; neste caso, {2,3,4, ...} é um subconjunto apropriado de {1,2,3, ...}.

Ao considerar estes objetos grandes, nós também pode querer ver se a noção de ordem contando coincide com o do cardeal acima definidos para estes conjuntos infinitos. Acontece que isso não acontece; considerando-se o exemplo acima, podemos ver que, se algum objeto "um maior do que o infinito" existe, então ele deve ter o mesmo cardinality que o jogo infinito nós começamos com. É possível utilizar uma noção formal de número diferente, chamada ordinais, com base nas idéias de contagem e considerando cada número, por sua vez, e descobrimos que as noções de cardinalidade e ordinalidade são divergentes, uma vez que sair dos números finitos.

Pode ser provado que a cardinalidade dos números reais é maior do que a dos números naturais que acabamos de descrever. Isto pode ser visualizado usando Argumento diagonal de Cantor; questões clássicas da cardinalidade (por exemplo, o hipótese do contínuo) estão preocupados com a descobrir se há alguma cardeal entre alguns par de outros cardeais infinitos. Em tempos mais recentes os matemáticos têm vindo a descrever as propriedades dos cardeais cada vez maiores.

Desde cardinalidade é um conceito tão comum em matemática, uma variedade de nomes estão em uso. Mesmice de cardinalidade é por vezes referido como equipotence, equipolência, ou equinumerosity. É, portanto, dizer que dois conjuntos com a mesma cardinalidade são, respectivamente, equipotente, equipolente, ou equinumerous.

Definição formal

Formalmente, assumindo o axioma da escolha, a cardinalidade de um conjunto X é o α menos ordinal de tal modo que há uma bijection entre X e α. Esta definição é conhecido como o von Neumann atribuição cardeal. Se o axioma da escolha não é assumido que precisamos fazer algo diferente. A definição mais antiga da cardinalidade de um conjunto X (implícito na Cantor e explícito em Frege e Principia Mathematica) é como o conjunto de todos os conjuntos que são equinumerous com X: isso não funciona em ZFC ou outros sistemas relacionados de teoria dos conjuntos axiomática , porque esta coleção é muito grande para ser um set, mas trabalha em escreva teoria e na Novas Fundações e sistemas relacionados. No entanto, se nós restringimos a partir desta classe para aqueles equinumerous com X que tem a menor posição, em seguida, ele vai trabalhar (isto é um truque devido a Dana Scott: ele funciona porque a coleção de objetos com qualquer grau dado é um conjunto).

Formalmente, a ordem entre números cardinais é definida da seguinte forma: | X | ≤ | Y | significa que existe um função injetiva de X para Y. O Cantor-Bernstein-Schroeder teorema afirma que, se | X | ≤ | Y | e | Y | ≤ | X | então | X | = | Y |. O axioma da escolha é equivalente à afirmação de que dado dois conjuntos X e Y, ou | X | ≤ | Y | ou | Y | ≤ | X |.

Um conjunto X é Dedekind-infinito se existe um subconjunto próprio Y de X com | X | = | Y | e Dedekind-finito se tal subconjunto não existe. O cardeais finitas são apenas os números naturais , ou seja, um conjunto X é finita se e somente se | X | = | n | n = n para algum número natural. Qualquer outro conjunto é infinito. Supondo que o axioma da escolha, pode ser provado que as noções de Dedekind correspondem aos padrões. Ele também pode ser provado que o cardeal 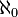(Aleph-0, onde Aleph é a primeira letra do Alfabeto hebraico, representada 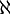) Do conjunto dos números naturais é a menor cardinal infinito, ou seja, qualquer conjunto infinito tem um subconjunto de cardinalidade O próximo cardeal maior é indicado por e assim por diante. Para cada α ordinal há um número cardinal e esta lista esgota todos os números cardinais infinitos.

Cardeal aritmética

Podemos definir aritméticas operações em números cardinais que generalizam as operações comuns para os números naturais. Pode ser mostrado que, para cardeais finitos destas operações coincidem com as operações usuais para números naturais. Além disso, estas operações partilham muitas propriedades com a aritmética comum.

Sucessor cardeal

Se o axioma da escolha detém, cada κ cardeal tem um sucessor κ ^+> κ, e não há cardeais entre κ e seu sucessor. Para cardeais finitos, o sucessor é simplesmente κ + 1. Para cardeais infinitos, o cardeal sucessor difere do ordinal sucessor.

Cardeal disso

Se X e Y são separado, adição é dada pela união de X e Y. Se os dois conjuntos são disjuntos já não, então eles podem ser substituídos por conjuntos disjuntos, isto é, substituir X por X × {0} e Y por Y × {1}.

Zero é um κ identidade aditivo + 0 = 0 + κ = κ.

Além é associativa (κ + μ) + ν = κ + (μ + ν).

Adição é comutativa κ + μ = μ + κ.

Além é não-decrescente em ambos os argumentos:

Se o axioma da escolha segura, além de números cardinais infinitos é fácil. Se qualquer 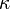ou 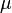é infinita, em seguida

Subtração

Se o axioma da escolha segura e dado uma σ cardinal infinito e um μ cardinal, haverá um cardinal κ tais que μ + κ = σ se e somente se μ ≤ σ. Vai ser exclusivo (e igual a σ) se e somente se μ <σ.

Cardeal multiplicação

O produto de cardeais vem do produto cartesiano.

κ · 0 = 0 · κ = 0.

κ · 0 = μ 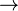(Κ = 0 ou μ = 0).

Um deles é um κ identidade multiplicativo · 1 = 1 · κ = κ.

A multiplicação é associativa (κ · μ) · ν = κ · (μ · ν).

A multiplicação é comutativa κ · μ = μ · κ.

A multiplicação é não-decrescente em ambos os argumentos: κ ≤ μ (Κ ν ≤ μ · · · ν e ν κ ≤ ν μ ·).

Multiplicação distribui mais de adição: κ · (μ + ν) = κ · μ + κ · ν e (μ + ν) · κ = μ · κ ν + · κ.

Se o axioma da escolha segura, a multiplicação de números cardinais infinitos também é fácil. Se quer κ ou μ é infinito e ambos são não-zero, em seguida,

Divisão

Se o axioma da escolha segura e dado uma π cardinal infinito e um μ cardeal não-zero, haverá um cardinal κ tais que μ · κ = π se e somente se μ ≤ π. Vai ser exclusivo (e igual a π) se e somente se μ <π.

Cardeal exponenciação

Exponenciação é dada por

onde ^X-Y é o conjunto de todas as funções de Y para X.

κ ⁰ = 1 (em particular 0 ⁰ = 1), ver função vazia.

Se uma ≤ μ, então 0 ^μ = 0.

1 ^μ = 1.

κ ¹ = κ.

^κ μ ^{ν +} = ^κ μ · κ ^ν.

^κ μ ^{· ν} = ^(κ μ) ^ν.

(Κ · μ) ^ν = κ ^ν · ^ν μ.

Se κ e μ são ambos finita e maior do que 1, e ν é infinita, em seguida, κ ^ν = μ ^ν.

Se κ é infinito e μ é finito e não-zero, então κ ^μ = κ.

Exponenciação é não-decrescente em ambos os argumentos:

(1 ≤ μ ν e κ ≤) 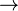^{(Μ ν κ} ≤ ^ν) e

(Κ ≤ μ) 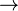^(Κ ν ≤ μ ν).

Note-se que 2 ^{| X |} é a cardinalidade do conjunto do conjunto X potência e Argumento diagonal de Cantor mostra que 2 ^{| X |>} | X | X para qualquer conjunto. Isso prova que não existe maior cardinal (porque para qualquer κ cardeais, podemos sempre encontrar um cardeal maior ^κ 2). Na verdade, o classe dos cardeais é um classe adequada.

Se o axioma da escolha segura e 2 ≤ κ e 1 ≤ μ e pelo menos um deles é infinito, então:

Max (κ, 2 ^μ) ≤ κ ^μ ≤ Max (2 ^κ, 2 ^μ).

Uso Teorema de König, pode-se provar κ <κ ^{cf (κ)} e κ <cf ^(κ 2) para quaisquer κ cardinais infinitos, onde cf (κ) é o cofinality de κ.

Nem raízes nem logaritmos pode ser definida exclusivamente por cardeais infinitos.

O logaritmo de um número infinito cardinal κ é definido como o número mínimo cardinal μ tal que κ ≤ 2 ^μ. Logaritmos de cardeais infinitos são úteis em alguns campos da matemática, por exemplo, no estudo de invariantes cardinais de espaços topológicos, embora eles não têm algumas das propriedades que logaritmos de números reais positivos possuem.

A hipótese do contínuo

O contínuo hipótese (CH) afirma que não há cardeais estritamente entr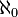e e Este último número cardeal também é muitas vezes designado por c; é o cardinalidade do continuum (o conjunto de números reais ). Neste caso O hipótese do continuum generalizada (GCH) afirma que para cada conjunto infinito X, não há cardeais estritamente entre | X | e 2 ^{| X |.} A hipótese do contínuo é independente dos axiomas usuais da teoria dos conjuntos, a Zermelo-Fraenkel axiomas juntamente com o axioma da escolha ( ZFC).