
Número natural
Informações de fundo
Esta seleção Wikipedia está offline disponível a partir de Crianças SOS, para distribuição no mundo em desenvolvimento. SOS Children trabalha em 45 países africanos; você pode ajudar uma criança em África ?
Em matemática , um número natural (também chamado de número de contagem) pode significar tanto um elemento do conjunto { 1 , 2, 3, ...} (o positivos inteiros ) ou um elemento do conjunto { 0 , 1, 2, 3, ...} (o inteiros não negativos). O primeiro é geralmente usado em teoria número , enquanto que o último é preferido em lógica matemática, teoria dos conjuntos , e ciência da computação . Veja abaixo para uma definição formal.
Números naturais têm duas finalidades principais: eles podem ser usados para contando ("existem três maçãs na tabela"), e que pode ser utilizado para ordenação ("esta é a 3ª maior cidade do país").
Propriedades dos números naturais relacionados com a divisibilidade , tais como a distribuição de números primos , são estudados na teoria dos números . Problemas relacionados com a contagem, como Teoria de Ramsey, são estudados em análise combinatória .

Histórico de números naturais eo estado de zero,
Os números naturais tiveram suas origens nas palavras usadas para contar as coisas, começando com o número um.
O primeiro grande avanço na abstração foi o uso de números para representar números. Isto permitiu que os sistemas a ser desenvolvido para a gravação de um grande número. Por exemplo, os babilônios desenvolveram um poderoso sistema de valor lugar assenta essencialmente nos numerais de 1 e 10. A antiga Egípcios tinham um sistema de números com distinta hieróglifos para 1, 10, e todas as potências de 10 até um milhão. Uma escultura em pedra de Karnak, que data de cerca de 1500 aC e agora no Do Louvre, em Paris, descreve como 276 2 centenas, dezenas, 7 e 6 queridos; e da mesma forma para o número 4622.
Um avanço muito mais tarde na abstração foi o desenvolvimento da idéia de zero, como um número com seu próprio numeral. Um zero dígitos tinha sido usada em notação lugar-valor tão cedo quanto 700 aC pelos babilônios, mas, eles omitiram-lo quando ele teria sido o último símbolo do número. O olmeca e civilização Maya utilizado zero como um número separado tão cedo quanto século 1 aC, aparentemente desenvolvida de forma independente, mas esse uso não se espalhou para além Mesoamérica. O conceito, usado em tempos modernos se originaram com a indiana matemático Brahmagupta em 628. No entanto, medieval computists (calculadoras de Páscoa ), começando com Dionísio Exiguus em 525, utilizado zero como um número sem usar um numeral romano para escrevê-lo. Em vez disso nullus, a palavra latina para "nada", foi empregado. O primeiro estudo sistemático de números como abstrações (isto é, como resumo entidades) é geralmente creditado aos gregos filósofos Pitágoras e Arquimedes . No entanto, estudos independentes também ocorreu em torno do mesmo tempo em Índia , China , e Mesoamérica.
No século XIX, um set-teórica definição de números naturais foi desenvolvido. Com esta definição, que era mais conveniente incluir de zero (o que corresponde à conjunto vazio) como um número natural. Esta convenção é seguido por set teóricos , lógicos e cientistas da computação . Outros matemáticos, principalmente teóricos dos números , muitas vezes preferem seguir a tradição mais antiga e considerar zero não ser um número natural.
Notação
Matemáticos usar N ou 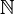 (Um N em negro corajoso, exibido como ℕ em Unicode) para se referir ao conjunto de todos os números naturais. Este conjunto é infinito contável: é infinito, mas contável por definição. Isso também é expressa dizendo que o número cardinal do conjunto é Módulo: Aleph_number ( falar · · hist · Links · subpages · testes - (Resultados)
(Um N em negro corajoso, exibido como ℕ em Unicode) para se referir ao conjunto de todos os números naturais. Este conjunto é infinito contável: é infinito, mas contável por definição. Isso também é expressa dizendo que o número cardinal do conjunto é Módulo: Aleph_number ( falar · · hist · Links · subpages · testes - (Resultados) 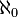 ).
).
Para ser inequívoca sobre se zero é incluído ou não, por vezes, um índice "0" é adicionado no primeiro caso, e um expoente "*" é adicionada em último caso:
- ℕ 0 = {0, 1, 2, ...}; ℕ * = {1, 2, ...}.
(Às vezes, um índice ou expoente "+" é adicionado para significar "positivo". No entanto, esta é muitas vezes usada para "não-negativo", em outros casos, como R + = [0, ∞) e Z + = {0, 1, 2, ...}, pelo menos na literatura Europeia. A notação "*", no entanto, é diferente de zero ou padrão para em vez elementos invertíveis.)
Alguns autores que excluem zero a partir os naturais usar os números inteiros prazo, denotadas 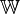 , Para o conjunto de inteiros não negativos. Outros usam a notação
, Para o conjunto de inteiros não negativos. Outros usam a notação 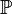 para os inteiros positivos.
para os inteiros positivos.
Definir teóricos muitas vezes denotar o conjunto de todos os números naturais por uma letra grega minúscula omega: ω. Quando esta notação é usada, zero é explicitamente incluída como um número natural.
Propriedades algébricas
| adição | multiplicação | |
| Encerramento: | a + b é um número natural | um × b é um número natural |
| associatividade : | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| comutatividade : | a + b = b + a | a × b = b um × |
| existência de uma elemento de identidade: | a + 0 = um | um × 1 = um |
| distributividade: | um × (b + c) = (a x b) + (c uma ×) | |
| Não divisores de zero: | Se a AB = 0, em seguida, a = 0 ou b = 0 (ou ambos) | |
Definições formais
Historicamente, a definição matemática precisa dos números naturais desenvolvido com alguma dificuldade. O Peano postula condições de estado que qualquer definição de sucesso deve satisfazer. Certas construções mostram que, dada a teoria dos conjuntos , deve existir modelos dos postulados Peano.
Axiomas de Peano
- Há um número natural 0.
- Cada um número natural tem um sucessor número natural, denotado por S (a).
- Não existe um número natural, cujo sucessor é 0.
- Números naturais distintos têm sucessores distintas: se um ≠ b, então S (a) ≠ S (b).
- Se uma propriedade é possuída por 0 e também pelo sucessor de cada número natural que possui, então ele é possuído por todos os números naturais. (Este postulado assegura que a técnica de prova indução matemática é válido.)
Deve notar-se que o "0" na definição acima não precisa corresponder ao que normalmente consideram ser o número zero. "0" significa simplesmente um objeto que, quando combinado com uma função sucessor adequado, satisfaz os axiomas de Peano. Todos os sistemas que satisfazem estes axiomas são isomorfos, o nome de "0" é usado aqui para o primeiro elemento, que é o único elemento que não é um sucessor. Por exemplo, os números naturais começando com um também satisfazer os axiomas.
Construções com base na teoria de conjuntos
A construção padrão
A construção padrão na teoria dos conjuntos , um caso especial do ordinal von Neumann construção, é definir os números naturais como segue:
- Montamos 0: = {}, o conjunto vazio,
- e definir S (a) = a ∪ {a} para cada um definido. S (a) é o sucessor de um, e S é chamado a função sucessor.
- Se o axioma do infinito detém, em seguida, o conjunto de todos os números naturais existe e é a intersecção de todos os conjuntos que contenham 0 que são fechadas sob esta função sucessor.
- Se o conjunto de todos os números naturais existe, em seguida, o mesmo satisfaz a Axiomas de Peano.
- Cada número natural é, então, igual ao conjunto dos números naturais menos do que isso, de modo que
- 0 = {}
- 1 = {0} = {{}}
- 2 = {0,1} = {0, 0} {} = {{}, {{}}}
- 3 = {0,1,2} = {0, {0}, {0, {0}}} = {{}, {} {}, {{}, {{}}}}
- {n = 0,1,2, ..., N -2, -1} n = {0,1,2, ..., N -2} ∪ {n = -1} (n -1) ∪ {n -1}
- e assim por diante. Quando você vê um número natural usado como um conjunto, este é tipicamente o que se entende. Segundo essa definição, há exatamente n elementos (no sentido ingênuo) no conjunto de n e n ≤ m (no sentido ingênuo) Se e apenas se n for um subconjunto de m.
- Além disso, com essa definição, diferentes interpretações possíveis de notações como R n (N-tuplas contra mapeamentos de n em R) coincidem.
- Mesmo se o axioma do infinito e não o conjunto de todos os números naturais não existe, é possível definir o que significa ser um desses conjuntos. Um conjunto n é um número natural significa que é ou 0 (vazio) ou um sucessor, e cada um dos seus elementos ou é 0 ou o sucessor de outro dos seus elementos.
Outras construções
Embora o padrão de construção é útil, não é a única construção possível. Por exemplo:
- pode-se definir 0 = {}
- e S (a) = {a},
- produtor
- 0 = {}
- 1 = {0} = {{}}
- 2 = {1} = {{{}}}, etc.
Ou podemos até definir 0 = {{}}
- e S (a) = U {a}
- produtor
- 0 = {{}}
- 1 = {{}, {0} = {}, {{}}}
- 2 = {{}, 0, 1}, etc.
Indiscutivelmente a definição mais antigo conjunto de teoria dos números naturais é a definição comumente atribuída a Frege e Russell em que cada um concreto número natural n é definido como o conjunto de todos os conjuntos com n elementos. Isto pode parecer circular, mas pode ser feito com cuidado rigorosa. Definir como 0 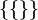 (Claramente o conjunto de todos os conjuntos com 0 elementos) e definir
(Claramente o conjunto de todos os conjuntos com 0 elementos) e definir 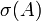 (Para qualquer conjunto A) como
(Para qualquer conjunto A) como 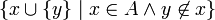 . Em seguida, 0 será o conjunto de todos os conjuntos com elementos 0,
. Em seguida, 0 será o conjunto de todos os conjuntos com elementos 0, 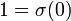 será o conjunto de todos os conjuntos com um elemento,
será o conjunto de todos os conjuntos com um elemento, 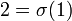 será o conjunto de todos os conjuntos, com dois elementos, e assim por diante. O conjunto de todos os números naturais pode ser definido como a intersecção de todos os conjuntos contendo 0 e como um elemento fechado sob
será o conjunto de todos os conjuntos, com dois elementos, e assim por diante. O conjunto de todos os números naturais pode ser definido como a intersecção de todos os conjuntos contendo 0 e como um elemento fechado sob 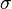 (Isto é, se o conjunto contém um elemento n, ele também contém
(Isto é, se o conjunto contém um elemento n, ele também contém 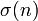 ). Esta definição não funciona nos sistemas habituais de teoria dos conjuntos axiomática porque as coleções envolvidos são muito grandes (que não vai funcionar em qualquer teoria dos conjuntos com a axioma da separação); mas trabalha em Novas Fundações (e em sistemas relacionados conhecidos para ser coerente) e em alguns sistemas de escreva teoria.
). Esta definição não funciona nos sistemas habituais de teoria dos conjuntos axiomática porque as coleções envolvidos são muito grandes (que não vai funcionar em qualquer teoria dos conjuntos com a axioma da separação); mas trabalha em Novas Fundações (e em sistemas relacionados conhecidos para ser coerente) e em alguns sistemas de escreva teoria.
Para o restante deste artigo, vamos acompanhar a construção padrão descrito acima.
Propriedades
Pode-se recursivamente definir uma adição sobre os números naturais, definindo a + 0 = A e A + S (b) S = (a + b) para todos a, b. Isso transforma os números naturais (N, +) em um comutativa monoid com 0 elemento de identidade, a chamada monoid livre com um gerador. Este monóide satisfaz a propriedade cancelamento e pode ser incorporado em um grupo . O grupo mais pequenas contendo os números naturais são os números inteiros .
Se nós definimos: 1 = S (0), em seguida b + b = 1 + S (0) = S (B + 0) = S (b). Ou seja, b + 1 é simplesmente o sucessor de b.
Analogamente, uma vez que a adição tem sido definida, a multiplicação × pode ser definido por meio de um x 0 = 0 e um S × (b) = (a x b) + a. Isso transforma (N *, ×) em um monoid comutativa livre com elemento de identidade 1; um grupo gerador para este monoid é o conjunto de números primos . A adição e multiplicação são compatíveis, o que é expresso no lei de distribuição de: a × (b + c) = (a x b) + (c uma ×). Estas propriedades de adição e multiplicação faz os números naturais uma instância de um comutativa semianel. Semirings são uma generalização algébrica dos números naturais onde multiplicação não é necessariamente comutativa.
Se interpretarmos os números naturais como "excluindo 0", e "a partir de 1", as definições de + e × são como acima, exceto que nós começamos com um + 1 = S (a) e um × 1 = a.
Para o restante do artigo, escrever ab para indicar a um produto × b, e também assumir o padrão ordem de operações.
Além disso, define-se um ordem total sobre os números naturais por escrito uma ≤ b se e somente se existe um outro número natural c com a + b = c. Esta ordem é compatível com as operações aritméticas da seguinte sentido: se a, b e c são números naturais e um ≤ b, então a + b + c ≤ C e AC ≤ BC. Uma propriedade importante dos números naturais é que eles são bem ordenada: cada conjunto não vazio de números naturais tem um elemento menos. O ranking entre os conjuntos bem ordenados é expressa por um número ordinal ; para os números naturais isto é expresso como " 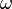 ".
".
Embora seja, em geral, não é possível dividir um número natural por outra e obter um número natural, como resultado, o procedimento de divisão com resto está disponível como um substituto: para qualquer dois números naturais a e b com b ≠ 0, podemos encontrar naturais números de q e r de tal modo que
- a = + BQ r e r <b
O número q é chamado o quociente e r é o chamado restante da divisão de a por b. Os números q e r são determinados exclusivamente por um e b. Este, o Algoritmo de divisão, é a chave para várias outras propriedades ( divisibilidade ), algoritmos (como o Algoritmo de Euclides), e idéias na teoria dos números.
Os números naturais, incluindo a forma de zero a monoid comutativa sob adição (com elemento de identidade zero), e sob a multiplicação (com elemento identidade um).
Generalizações
Dois generalizações de números naturais surgem das duas utilizações:
- Um número natural pode ser utilizada para expressar o tamanho de um conjunto finito; mais geralmente um número cardinal é uma medida para o tamanho de um conjunto também adequado para conjuntos infinitos; esta refere-se a um conceito de "tamanho" de tal modo que se houver uma bijection entre dois conjuntos têm o mesmo tamanho. O conjunto dos números naturais em si e qualquer outro conjunto infinito contável tem cardinalidade Módulo: Aleph_number ( falar · · hist · Links · subpages · testes - Resultados)
( 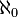 ).
).
- Os números ordinais "primeiro", "segunda", "terceiro" pode ser atribuído aos elementos de um conjunto finito totalmente ordenado, e também para os elementos de bem ordenados conjuntos infinitos contáveis como o conjunto de números naturais em si. Isto pode ser generalizada para números ordinais que descrevem a posição de um elemento de uma ordem bem definida em geral. Um número ordinal também é usado para descrever o "tamanho" de um conjunto bem ordenada, num sentido diferente do cardinalidade: se houver uma isomorfismo ordem entre dois conjuntos bem ordenados que têm o mesmo número ordinal. O primeiro número ordinal que não é um número natural é expressa como
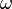 ; este é também o número ordinal do conjunto de números naturais em si.
; este é também o número ordinal do conjunto de números naturais em si.
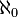 e
e 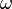 têm de ser distinguidas porque muitos conjuntos bem ordenados com número cardinal
têm de ser distinguidas porque muitos conjuntos bem ordenados com número cardinal 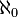 tem um número de ordem mais elevada do que
tem um número de ordem mais elevada do que 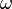 , Por exemplo,
, Por exemplo, 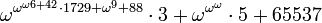 ;
; 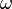 é o valor mais baixo possível (o ordinal inicial).
é o valor mais baixo possível (o ordinal inicial).
Para conjuntos bem ordenados finitos há one-to-one correspondência entre o número ordinal e cardeal; Por conseguinte, ambos podem ser expressos pelo mesmo número natural, o número de elementos do conjunto. Este número pode também ser usado para descrever a posição de um elemento numa maior finito, ou um infinito, sequência .
Outros generalizações são discutidos no artigo sobre números .

