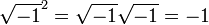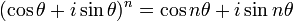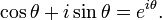Número

Um número é uma objeto abstrato, sinais de que são símbolos usados em contagem e medição . Um símbolo que representa um número é chamado um numeral, mas no uso comum o número palavra é usada tanto para o objeto abstrato eo símbolo. Em adição à sua utilização na contagem e medição, numerais são muitas vezes utilizados para as etiquetas ( números de telefone), por encomenda ( números de série), e por códigos ( ISBN). Em matemática , a definição do número foi ampliado ao longo dos anos para incluir esses números como nulo , os números negativos , os números racionais , números irracionais e números complexos .

Certos procedimentos que a entrada de um ou mais números e saída de um número são chamados numérica operações. Input operações Unário um número único e de saída de um único número. Por exemplo, a operação adiciona um sucessor para um número inteiro: o sucessor de 4 é 5. são mais comuns operações binárias que entrada e saída de dois números de um único número. Exemplos de operações binárias incluem adição , subtração , multiplicação , divisão , e exponenciação . O estudo de operações numéricas é chamado aritmética .

O ramo da matemática que estuda sistemas de números abstratos como grupos , anéis e campos é chamado de álgebra abstrata .

Tipos de números

Os números podem ser classificados em conjuntos, chamados de sistemas de número . (Para diferentes métodos de expressar números com símbolos, como os algarismos romanos , ver sistemas numéricos .)

Números naturais

Os números mais conhecidos são os números naturais ou contagem números: um, dois, três, .... Algumas pessoas também incluem zero nos números naturais; no entanto, outros não.

Na base dez sistema numérico, em uso quase universal hoje para operações aritméticas, os símbolos para os números naturais são escritas usando dez dígitos : 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Nesta base do sistema dez, o dígito mais à direita de um número natural tem um valor de lugar de um, e todos os outros dígito tem um valor lugar dez vezes maior que o valor de lugar do dígito à sua direita. O símbolo para o conjunto de todos os números naturais é N, também escrito .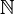

Inteiros

Os números negativos são números que são menos do que zero. Eles são o oposto de números positivos. Por exemplo, se um número positivo indica um depósito bancário, em seguida, um número negativo indica uma retirada do mesmo montante. Os números negativos são geralmente escritos por escrever um sinal negativo em frente ao número que eles são o oposto de. Deste modo, o oposto da 7 é escrito -7. Quando o conjunto dos opostos dos números naturais é combinado com os números naturais e zero, obtém-se os inteiros Z (alemão Zahl, plural zahlen), também escrito .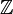

Números racionais

Um número racional é um número que pode ser expressa como uma fracção de um número inteiro com o numerador e um número natural diferente de zero denominador . A fracção de m / n ou

m representa partes iguais, onde partes iguais de n que o tamanho compõem um todo. Duas fracções diferentes podem corresponder ao mesmo número racional; por exemplo, 1/2 e 2/4 são iguais, isto é:

.

Se o valor absoluto de m é maior do que n, então o valor absoluto da fracção é superior a 1. As fracções pode ser maior do que, menos do que, ou igual a 1, e também pode ser positivo, negativo ou nulo. O conjunto de todas as frações inclui os inteiros, uma vez que cada número inteiro pode ser escrito como uma fração com denominador 1. Por exemplo -7 pode ser escrito -7/1. O símbolo para os números racionais é Q (para quociente), também escrito .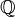

Números reais

Os números reais incluem todos os números de medição. Os números reais são geralmente escritos usando decimais numerais, em que um ponto decimal é colocado à direita do dígito com valor lugar um. À direita da vírgula, cada dígito tem um valor local de um décimo do valor lugar do dígito à sua esquerda. Assim

representa uma centena, duas dezenas, 3 queridos, 4/10, 5/100 e 6/1000. Ao dizer o número, o decimal é lida "point", assim: "um dois três ponto quatro, cinco, seis". Em, por exemplo, os EUA e Reino Unido, o decimal é representado por um período, na Europa continental por um vírgula. Zero é muitas vezes escrito como 0.0 e negativos números reais são escritos com um precedente sinal de menos:

.

Todo número racional é também um número real. Para escrever uma fração como um decimal, divida o numerador pelo denominador. Não é o caso, no entanto, que cada número real é racional. Se um número real não pode ser escrito como uma fracção de dois números inteiros, é chamado irracional . Um decimal que pode ser escrita como uma fração ou extremidades (terminar) ou para sempre se repete, porque é a resposta a um problema na divisão. Assim, o número real de 0,5 pode ser escrita como meia eo real número 0.333 ... (trios repetir para sempre) pode ser escrita como 1/3. Por outro lado, o número real π ( pi ), a razão entre o circunferência de qualquer círculo e seu diâmetro , é

.

Uma vez que a casa decimal nem termina nem sempre se repete, não pode ser escrito como uma fracção, e é um exemplo de um número irracional. Outros números irracionais incluem

(O raiz quadrada de 2, que é, o número positivo cujo quadrado é 2).

Assim como frações podem ser escritos em mais de uma maneira, também pode decimais. Por exemplo, se multiplicar ambos os lados da equação

por três, descobrimos que

.

Assim 1.0 e 0,999 ... são dois números diferentes decimais que representam o número natural 1. Há um número infinito de outras formas de representar o número 1, por exemplo, 2/2, 3/3, 1,00, 1,000, e assim por diante.

Cada número real é racional ou irracional. Cada número real corresponde a um ponto no linha número. Os números reais também têm uma propriedade importante, mas altamente técnica chamada propriedade limite superior mínimo. O símbolo para os números reais é R ou .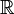

Quando um número real representa uma medição , há sempre uma margem de erro . Isso é muitas vezes indicada por arredondamento ou truncar uma casa decimal, de modo que os dígitos que sugerem uma precisão maior do que a medida em si são removidos. Os dígitos restantes são chamados algarismos significativos. Por exemplo, medidas com uma régua raramente pode ser feita sem uma margem de erro é de pelo menos 0,01 metros. Se os lados de um rectângulo são medidos como 1,23 metros e 4,56 metros, seguida de multiplicação dá uma área para o rectângulo de 5,6088 metros quadrados. Uma vez que apenas os dois primeiros dígitos depois do ponto decimal são significativos, isso geralmente é arredondado para 5,61.

Em álgebra abstrata , os números reais são caracterizados exclusivamente por ser o único completamente pedido campo. Eles não são, no entanto, uma corpo algebricamente fechado.

Os números complexos

Movendo-se para um nível maior de abstração, os números reais podem ser estendidas aos números complexos . Este conjunto de números surgiu, historicamente, a partir da questão de saber se um número negativo pode ter uma raiz quadrada . Isto levou à invenção de um novo número: a raiz quadrada de um negativo, indicado por I , o símbolo designado por Leonhard Euler , e chamado a unidade imaginária . Os números complexos consistem em todos os números de forma

em que a e b são números reais. Na expressão a + bi, o número real um é chamado a parte real e bi é chamada a parte imaginária. Se a parte real de um número complexo é zero, então o número chamado é uma número imaginário ou é referido como puramente imaginárias; Se a parte imaginária é zero, então o número é um número real. Assim, os números reais são um subconjunto dos números complexos. Se as partes real e imaginária de um número complexo são ambos números inteiros, em seguida, o número é chamado um Número inteiro de Gauss. O símbolo para os números complexos é C ou .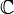

Em álgebra abstrata , os números complexos são um exemplo de um corpo algebricamente fechado, o que significa que cada polinômio com complexo coeficientes podem ser tidos em fatores lineares. Como o sistema de número real, o sistema de número complexo é um campo e é completar, mas ao contrário dos números reais não é ordenada. Ou seja, não há sentido em dizer que i é maior que 1, nem há qualquer sentido em dizer que que i é menor que 1. Em termos técnicos, os números complexos não têm a propriedade tricotomia .

Os números complexos correspondem a pontos no plano complexo , chamado às vezes o plano de Argand.

Cada um dos sistemas acima mencionados é o número um subconjunto apropriado do seguinte sistema de numeração. Simbolicamente, N ⊂ Z ⊂ Q ⊂ R ⊂ C.

Outros tipos

Superreal, hiper-real e números surreais estender os números reais adicionando infinitamente pequenos números e infinitamente grande número, mas ainda formam campos.

A idéia por trás p-adic números é esta: Embora os números reais podem ter expansões infinitamente longos à direita do ponto decimal, estes números permitem infinitamente longas expansões para a esquerda. O sistema de numeração que resulta depende de que base é utilizada para os dígitos: qualquer base é possível, mas um sistema com as melhores propriedades matemáticas é obtido quando a base é um número primo .

Para lidar com conjuntos infinitos, os números naturais foram generalizados para os números ordinais e para os números cardinais . O primeiro dá a ordenação da coleção, enquanto o segundo dá o seu tamanho. Para o conjunto finito, os números ordinais e cardinais são equivalentes, mas diferem no caso infinito.

Há também outros conjuntos de números com usos especializados. Alguns são subconjuntos dos números complexos. Por exemplo, números algébricos são as raízes de polinômios com racional coeficientes. Os números complexos que não são algébrica são chamados números transcendentes.

Conjuntos de números que não são subconjuntos dos números complexos são chamados às vezes números hypercomplex. Eles incluem o quaternions H, inventado por Sir William Rowan Hamilton, em que a multiplicação não é comutativa , eo octoniões, em que a multiplicação não é associativas . Elementos de campos de função de não nula se comportam característica em alguns aspectos, como números e são muitas vezes consideradas como números por teóricos dos números.

Numerais

Os números devem ser distinguidos de numerais, os símbolos usados para representar números. O número cinco pode ser representado por tanto a base dez numeral '5' e pelo numeral romano "V". Notações usadas para representar números são discutidas no artigo sistemas numerais . Um desenvolvimento importante na história da numerais foi o desenvolvimento de um sistema de posicionamento, como decimais modernos, que podem representar números muito grandes. Os algarismos romanos exigem símbolos adicionais para números maiores.

História

Histórico de números inteiros

Os primeiros números

Especula-se que o primeiro uso conhecido de números remonta a cerca de 30000 aC, ossos ou outros artefatos foram descobertos com marcas de corte em que eles são muitas vezes consideradas marcas de registro. O uso destas marcas de registro têm sido sugeridos para ser qualquer coisa de contagem do tempo decorrido, tais como números de dias, ou manter registros de valores.

Sistemas de computação não conceito de valor-lugar (como na notação decimal actualmente utilizado), o que limita a sua representação de grandes números e, como tal, é muitas vezes considerado que este é o primeiro tipo de sistema de resumo que seriam utilizados, e pode ser considerado um sistema de numeração.

O primeiro sistema conhecido com valor lugar foi o Mesopotâmica sistema de base 60 (ca. 3400 aC) e do sistema mais antigo base conhecida 10 datas para 3100 aC no Egito .

História zero

A utilização de zero como um número deve ser distinguido do seu uso como um marcador de posição no numeral sistemas de valor local. Muitos antigos textos indianos usar um sânscrito palavra Shunya para se referir ao conceito de vazio; em textos de matemática esta palavra muitas vezes ser utilizado para referir o número zero. . Na mesma linha, Pāṇini ( Século 5 aC) usou a () operador nulo zero (ou seja, uma produção lambda) no Ashtadhyayi, sua gramática algébrica para o sânscrito língua. (Veja também Pingala)

Os registros mostram que os gregos antigos parecia incerto sobre o status do zero como um número: eles se perguntaram "como pode" nada "ser alguma coisa?" levando a interessante filosófica e, pelo período Medieval, argumentos religiosos sobre a natureza ea existência de zero eo vácuo. O paradoxos da Zenão de Elea dependem em grande parte sobre a interpretação incerta de zero. (Os antigos gregos chegaram a questionar se um era um número.)

O final dos olmecas pessoas do centro-sul do México começaram a usar um verdadeiro zero (um glifo shell) no Novo Mundo, possivelmente, pelo Quarto século aC, mas certamente por 40 aC, que se tornou parte integrante da Numerais maias e os Maya calendário, mas não influenciou sistemas numerais Velho Mundo.

Por 130, Ptolomeu , influenciado por Hiparco e os babilônios, estava usando um símbolo para zero (um pequeno círculo com uma longa barra superior) dentro de um sistema numérico sexagesimal de outra forma usando alfabética Numerais gregos. Porque foi usado por si só, não apenas como um espaço reservado, este De zero helenístico foi o primeiro uso documentado de um verdadeiro zero no Velho Mundo. Em posteriores bizantinos manuscritos de seu Syntaxis Mathematica (Almagesto), a zero, helenística tinha se transformado na letra grega omicron (caso contrário, o que significa 70).

Outra zero real foi utilizado em mesas ao lado de algarismos romanos por 525 (primeiro uso conhecido por Dionísio Exiguus), mas como uma palavra, nulla significa nada, não como um símbolo. Quando a divisão produziu zero como um resto, nihil, também significando nada, foi usada. Estes zeros medievais foram usados por todos os futuros medieval computists (calculadoras de Páscoa ). Um uso isolado de sua inicial, N, foi usada em uma tabela de números romanos por Bede ou um colega sobre 725, um verdadeiro símbolo zero.

Um uso documentado mais cedo do zero Brahmagupta (no Brahmasphutasiddhanta) data de 628. Ele tratou zero como um número e operações envolvendo ele discutidas, incluindo divisão. Por esta altura (século 7) o conceito tinha claramente alcançado Camboja , e documentação mostra a idéia mais tarde, espalhando-se para a China eo islâmico mundo.

Histórico de números negativos

O conceito abstrato de números negativos foi reconhecido mais cedo 100 aC - 50 BC. Os chineses " Nove Capítulos da Arte Matemática "(Jiu-Zhang Suanshu) contém métodos para encontrar as áreas de figuras; hastes vermelhas foram usadas para denotar positiva coeficientes, preto para negativo. Esta é a primeira menção conhecida de números negativos no Oriente; a primeira referência em uma obra ocidental foi no século 3 em Grécia . Diofante referida equação equivalente a (A solução seria negativo) em Aritmética, dizendo que a equação deu um resultado absurdo.

Durante o 600s, os números negativos estavam em uso na Índia para representar dívidas. Diofanto 'de referência anterior foi discutido de forma mais explícita pelo matemático indiano Brahmagupta, em Brahma-Sphuta-Siddhanta 628, que usou números negativos para produzir a forma geral fórmula quadrática que permanece em uso hoje. No entanto, no século 12 na Índia, Bhaskara dá raízes negativas para equações de segundo grau, mas diz que o valor negativo "é, neste caso, não deve ser tomada, porque é inadequada, as pessoas não aprovam raízes negativas."

Europeias matemáticos, em sua maior parte, resistiu o conceito de números negativos até o século 17 , embora Fibonacci permitiu soluções negativas em problemas financeiros onde eles poderiam ser interpretadas como débitos (capítulo 13 Liber ábacos, 1202) e mais tarde como perdas (em Flos). Ao mesmo tempo, os chineses foram indicando os números negativos pelo desenho de um curso diagonal através do dígito mais à direita não zero de numeral do número positivo correspondente. O primeiro uso de números negativos em uma obra europeia foi de Chuquet durante o século 15 . Ele usou como expoentes , mas referiu a eles como "números absurdos".

Tão recentemente quanto o século 18 , a Swiss matemático Leonhard Euler acreditava que os números negativos foram maiores do que o infinito , e era comum a prática de ignorar quaisquer resultados negativos retornados por equações com base no pressuposto de que eles eram sem sentido, assim como René Descartes fez com soluções negativas num sistema de coordenadas cartesiano .

Histórico de números racionais, irracionais e reais

Histórico de números racionais

É provável que o conceito de números fraccionários datas de tempos pré-históricos. Mesmo o Os antigos egípcios escreveu textos de matemática que descreve como converter gerais frações em sua notação especial. Matemáticos gregos e indianos clássicos feitos estudos sobre a teoria dos números racionais, como parte do estudo geral da teoria dos números . A mais conhecida delas é Elementos de Euclides , que data de cerca de 300 aC. Dos textos indianos, o mais relevante é o Sthananga Sutra, que abrange também a teoria dos números, como parte de um estudo geral da matemática.

O conceito de frações decimais está intimamente ligada com a notação valor decimal; os dois parecem ter desenvolvido em conjunto. Por exemplo, é comum que os sutras matemática Jain para incluir cálculos de aproximações-fração decimal para pi ou a raiz quadrada de dois. Da mesma forma, os textos de matemática babilônica tinha sempre utilizado frações sexagesimais com grande freqüência.

Histórico de números irracionais

O primeiro uso conhecido de números irracionais foi no Índico Sulba Sutras compostas entre 800- 500 aC. As primeiras provas existência de números irracionais é geralmente atribuída a Pitágoras , mais especificamente para o Pitagórico Hippasus de Metapontum, que produziu um (geométrica mais provável) a prova da irracionalidade do raiz quadrada de 2. A história diz que Hippasus descoberto números irracionais quando se tenta representar a raiz quadrada de 2 como uma fração. No entanto Pitágoras acreditava na incondicionalidade de números, e não podia aceitar a existência de números irracionais. Ele não podia negar a sua existência através da lógica, mas suas crenças não aceitaria a existência de números irracionais e por isso ele condenado Hippasus a morte por afogamento.

O século XVI viu a aceitação final por europeus de negativos , integrais e fracionários números. O século XVII viu frações decimais com a notação moderna bastante geralmente usado por matemáticos. Mas não foi até o século XIX que os irracionais foram separados em partes algébricas e transcendentes, e um estudo científico da teoria da irracionais foi feita mais uma vez. Ele tinha permanecido quase adormecida desde Euclides . O ano de 1872 viu a publicação das teorias de Karl Weierstrass (por seu aluno Kossak), Heine ( Crelle, 74), Georg Cantor (Annalen, 5), e Richard Dedekind. Meray tinha tomado em 1869 o mesmo ponto de partida, Heine, mas a teoria é geralmente referido o ano 1872. método de Weierstrass foi completamente estabelecido pela Salvatore Pincherle (1880), e de Dedekind tem recebido destaque adicional através do trabalho do autor mais tarde (1888) ea recente aprovação pelo Paul Tannery (1894). Weierstrass, Cantor e Heine baseiam suas teorias sobre séries infinitas, enquanto Dedekind funda sua sobre a ideia de um cortar (Schnitt) no sistema de números reais , separando todas números racionais em dois grupos tendo certas propriedades características. O assunto tem recebido contribuições posteriores nas mãos de Weierstrass, Kronecker (Crelle, 101), e Meray.

Frações contínuas, estreitamente relacionadas com números irracionais (e devido a Cataldi, 1613), recebeu atenção nas mãos de Euler , e no início do século XIX, foram trazidos à proeminência através dos escritos de Joseph Louis Lagrange . Outras contribuições notáveis foram feitas por Druckenmüller (1837), Kunze (1857), Lemke (1870), e Günther (1872). Ramus (1855) conectado pela primeira vez o assunto com determinantes , resultando, com as contribuições subsequentes de Heine, Möbius, e Günther, na teoria da Kettenbruchdeterminanten. Dirichlet também adicionado à teoria geral, assim como inúmeros contribuintes para as aplicações do assunto.

Números transcendentes e reais

Os primeiros resultados relativos a números transcendentais foram 1.761 prova de Lambert que π não pode ser racional, e também que o e ⁿ é irracional se n é racional (a menos que n = 0). (A constante e foi submetido pela primeira vez no 1618 O trabalho de Napier em logaritmos .) Legendre estendido para esta prova mostrou que π não é a raiz quadrada de um número racional. A busca por raízes de quintic e equações de grau superior foi um desenvolvimento importante, o Abel-Ruffini teorema ( Ruffini 1799, Abel 1824) mostrou que eles não podia ser resolvido por radicais (fórmula envolvendo apenas as operações aritméticas e raízes). Por isso, foi necessário considerar o conjunto mais vasto de números algébricos (todas as soluções para equações polinomiais). Galois (1832), ligado equações polinomiais a teoria do grupo que deu origem ao campo da teoria de Galois .

Até mesmo o conjunto de números algébricos não foi suficiente eo conjunto completo de número real inclui números transcendentes. A existência de que foi estabelecido pela primeira vez por Liouville (1844, 1851). Hermite provou em 1873 que e é transcendental e Lindemann provou em 1882 que π é transcendental. Finalmente Cantor mostra que o conjunto de todos os números reais é uncountably infinito, mas o conjunto de todos números algébricos é infinito contável, para que haja um número incontável infinito de números transcendentais.

Infinito

A mais antiga conhecida da concepção matemático infinito aparece no Yajur Veda, que a certa altura afirma: "se você remover uma parte do infinito ou adicionar uma parte para o infinito, ainda que permanece é infinito". Borda infinita foi um tema popular de estudo filosófico entre o Jain matemáticos circa 400 aC. Eles distinguiram entre cinco tipos de infinito: infinito em uma e duas direções, infinitos na área, infinito em todos os lugares, e infinito perpetuamente.

No Ocidente, a noção tradicional de infinito matemático foi definida por Aristóteles , que distinguiu infinito real e potencial infinito; o consenso geral, sendo que apenas o último teve verdadeiro valor. Galileo 's Duas Novas Ciências discutido a idéia de um-para-um correspondências entre conjuntos infinitos. Mas o próximo grande avanço na teoria foi feita por Georg Cantor ; em 1895 , ele publicou um livro sobre sua nova teoria dos conjuntos , que institui, entre outras coisas, a hipótese do contínuo.

Uma versão moderna geométrica do infinito é dado por geometria projetiva, que introduz "pontos ideais no infinito", uma para cada direção espacial. Cada família de linhas paralelas numa dada direcção é postulado que convergem para o ponto ideal correspondente. Isto está intimamente relacionado com a idéia de pontos de fuga em desenho em perspectiva.

Os números complexos

A mais antiga referência fugaz ao quadrado raízes de números negativos ocorreram no trabalho do matemático e inventor Heron de Alexandria, no século 1 dC, quando ele considerou o volume de um impossível tronco de uma pirâmide . Tornaram-se mais proeminente quando no século 16 fórmulas fechadas para as raízes de polinômios terceiro e quarto graus foram descobertos por matemáticos italianos (ver Niccolo Fontana Tartaglia, Gerolamo Cardano). Ele logo percebeu que estas fórmulas, mesmo se um só estava interessado em soluções reais, por vezes necessária a manipulação de raízes quadradas de números negativos.

Este foi duplamente preocupante, uma vez que nem sequer considerar os números negativos para ser em terra firme na época. O termo "imaginário" para estas quantidades foi cunhado por René Descartes em 1637 e foi concebido para ser pejorativo (veja número imaginário para uma discussão sobre a "realidade" dos números complexos). Uma outra fonte de confusão foi que a equação

parecia ser caprichosamente incompatível com a identidade algébrica

,

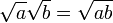que é válido para positivo números reais e b, e que também foi utilizado em cálculos com números complexos com um de a, b positivo e outro negativo. O uso incorreto desta identidade, ea identidade relacionados

no caso em que tanto a como b são negativos, mesmo bedeviled Euler . Esta dificuldade, eventualmente, levou-o para a convenção de usar o símbolo especial i no lugar de √-1 para se proteger contra este erro.

O século 18 viu o trabalho dos Abraham de Moivre e Leonhard Euler . Para De Moivre é devido (1730) a fórmula bem conhecida que leva seu nome, A fórmula de de Moivre:

e Euler (1748) Fórmula de Euler análise complexa:

A existência de números complexos não foi completamente aceite até que a interpretação geométrica tinha sido descrito por Caspar Wessel em 1799 ; foi redescoberto vários anos mais tarde e popularizado por Carl Friedrich Gauss , e como resultado, a teoria dos números complexos recebeu uma notável expansão. A idéia da representação gráfica dos números complexos tinha aparecido, no entanto, já em 1685, em De Algebra tractatus de Wallis.

Também em 1799, Gauss forneceu a primeira prova geralmente aceite do teorema fundamental da álgebra, mostrando que todo polinômio sobre os números complexos tem um conjunto completo de soluções em que reino. A aceitação geral da teoria dos números complexos não é um pouco devido aos trabalhos de Augustin Louis Cauchy e Niels Henrik Abel, e especialmente o último, que foi o primeiro a usar corajosamente números complexos com um sucesso que é bem conhecido.

Gauss estudou números complexos de forma a + bi, onde a e b são integrais, ou racional (e i é uma das duas raízes de x ² + 1 = 0). Seu aluno, Ferdinand Eisenstein, estudou o tipo a + bω, onde ω é uma raiz complexa de x ^3-1 = 0. Outros essas classes (chamado campos ciclotômicos) de números complexos são derivados da raízes da unidade x ^k - 1 = 0 para valores maiores de k. Esta generalização é em grande parte devido à Ernst Kummer, que também inventou números ideais, que foram expressas como entidades geométricas por Felix Klein em 1893. A teoria geral dos campos foi criado por Évariste Galois, que estudaram os campos gerados pelas raízes de qualquer equação polinomial F (x) = 0.

Em 1850 Victor Alexandre Puiseux deu o passo chave de distinguir entre postes e pontos de ramificação, e introduziu o conceito de pontos singulares essenciais; este levaria eventualmente ao conceito da alargado plano complexo.

Números primos

Os números primos foram estudados ao longo da história. Euclides dedicou um livro dos elementos para a teoria dos números primos; em que ele provou a infinitude dos primos eo teorema fundamental da aritmética , e apresentou o Algoritmo de Euclides para encontrar o máximo divisor comum de dois números.

Em 240 aC, Eratóstenes usou o Crivo de Eratóstenes para isolar rapidamente os números primos. Mas a maioria ainda mais o desenvolvimento da teoria dos números primos na Europa remonta ao Renascimento e épocas posteriores.

Em 1796 , Adrien-Marie Legendre conjecturou o teorema de número primo, descrevendo a distribuição assintótica dos números primos. Outros resultados referentes à distribuição dos números primos incluem prova de Euler que a soma dos inversos dos primos diverge, ea conjectura de Goldbach , que afirma que qualquer número suficientemente grande mesmo é a soma de dois números primos. No entanto, outra conjectura relacionada com a distribuição dos números primos é o Hipótese de Riemann, formulada por Bernhard Riemann em 1859 . O teorema de número primo foi finalmente provado por Jacques Hadamard e Charles de la Vallée-Poussin em 1896 .