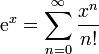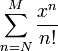Número real

Em matemática , os números reais podem ser descritas informalmente como números que podem ser dadas por um infinito representação decimal, como 2,4871773339 .... Os números reais incluem tanto os números racionais , tais como 42 e -23 / 129, e números irracionais , tais como π ea raiz quadrada de 2, e pode ser representado como pontos ao longo de um comprimento infinito linha número.

Uma definição mais rigorosa dos números reais foi um dos acontecimentos mais importantes do século 19 de matemática. Definições mais populares em uso hoje incluem classes de equivalência de Seqüências de Cauchy de números racionais, Cortes de Dedekind, uma versão mais sofisticada de "representação decimal", e uma definição axiomática dos números reais como o único completo Arquimedes pedido campo.

Os números reais nome surgiu para distingui-los de que era então chamado números imaginários (e agora os números complexos ).

Propriedades básicas

Um número real pode ser racional ou irracional ; ou algébrica ou transcendental; e também positivo, negativo ou nulo .

Números reais medida quantidades contínuas. Eles podem, em teoria, ser expressa por representações decimais que têm uma sequência infinita de dígitos para a direita do ponto decimal; estas são muitas vezes representado na mesma forma como 324,823211247 ... O reticências (três pontos) indicam que ainda haveria mais dígitos para vir.

Mais formalmente, números reais tem as duas propriedades básicas de ser um campo ordenado, e ter a propriedade limite superior mínimo. A primeira diz que números reais compreendem um campo, com adição e multiplicação, bem como a divisão por números diferentes de zero, o que pode ser totalmente ordenado em uma linha de número de uma maneira compatível com a adição e multiplicação. O segundo diz que, se um conjunto não vazio de números reais tem um limite superior, então ele tem um menor limite superior. Estes dois juntos definem os números reais completamente, e permitir que suas outras propriedades a ser deduzido. Por exemplo, podemos provar a partir destas propriedades que todo polinômio de grau ímpar com coeficientes reais tem uma raiz real, e que, se você adicionar a raiz quadrada de -1 para os números reais, obtendo os números complexos , o resultado é algebricamente fechado.

Usos

Medidas nas ciências físicas são quase sempre concebido como aproximações de números reais. Embora os números utilizados para esta finalidade são geralmente frações decimais representativas de números racionais, escrevê-las em termos decimais sugere que eles são uma aproximação para um número real teórico subjacente.

Um número real é dito ser calculável se existe um algoritmo que gera os dígitos. Porque não são apenas countably muitos algoritmos, mas um número incontável de reais, a maioria dos números reais não são computáveis. Alguns construtivistas aceitar a existência de apenas os reais que são computáveis. O conjunto de números definíveis é mais ampla, mas ainda só contável.

Computadores só pode aproximar a maioria dos números reais. Mais comumente, eles podem representar um determinado subconjunto de os racionais exatamente, quer através de números de ponto flutuante ou números de ponto fixo, e esses números racionais são usados como uma aproximação para outros valores reais nas proximidades. Aritmética de precisão arbitrária é um método para representar números racionais arbitrárias, limitado apenas pela disponível memória, mas mais vulgarmente utiliza um de um número fixo de bits de precisão determinado pelo tamanho do registradores do processador. Para além destes valores racionais, sistemas de álgebra computacional é capaz de tratar vários (contáveis) números irracionais exatamente armazenando uma descrição algébrica (como "sqrt (2)") ao invés de sua aproximação racional. Note-se que algumas linguagens de programação usar "real" para descrever a sua principal numérico tipo de dados, tal como AppleScript.

Os matemáticos usam o símbolo R (ou, em alternativa, 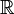, A letra " R "em negro corajoso, Unicode ℝ) para representar o um conjunto de números reais. O notação R ⁿ refere-se a uma N - espaço dimensional com coordenadas reais; por exemplo, um valor de R ³ consiste de três números reais e especifica uma localização no espaço 3-dimensional.

Em matemática, real é utilizado como um adjectivo, significa que o campo subjacente é o campo de números reais. Por exemplo verdadeira matriz , verdadeiro polinômio e real Deite álgebra. Como um substantivo, o termo é usado quase que estritamente em referência aos números reais, eles próprios (por exemplo, O "conjunto de todos os reais").

História

Fracções vulgares tinha sido usado pelo Egípcios em torno de 1000 aC; o Védica " Sulba Sutras "(" Estado de acordes "em sânscrito ), ca. 600 aC, incluem o que pode ser o primeiro «utilização» dos números irracionais .

Em torno de 500 aC, os gregos matemáticos liderados por Pitágoras percebeu a necessidade de números irracionais , em particular, a irracionalidade do raiz quadrada de dois.

Nos 18 e 19 séculos havia muito trabalho no irracional e números transcendentes. Lambert (1761) deu a primeira prova de falhas que π não pode ser racional, Legendre (1794) completado a prova, e mostraram que π não é a raiz quadrada de um número racional. Ruffini (1799) e Provas Abel (1842), ambos construídos de Abel-Ruffini teorema: que o general equações de quinto grau ou superior não pode ser resolvido por uma fórmula geral envolvendo apenas as operações aritméticas e raízes.

Évariste Galois (1832) desenvolveram técnicas para determinar se uma determinada equação pode ser resolvida por radicais que deram origem ao campo da teoria de Galois . Joseph Liouville (1840) mostrou que nem e nem e ² pode ser uma raiz de um número inteiro equação quadrática , e em seguida, estabeleceu a existência de números transcendentais, a prova sendo posteriormente deslocado por Georg Cantor (1873). Charles Hermite (1873), primeiro provou que e é transcendental, e Ferdinand von Lindemann (1882), mostrou que π é transcendental. A prova de Lindemann foi muito simplificada por Weierstrass (1885), ainda mais por David Hilbert (1893) e, finalmente, foi feita por elementar Hurwitz e Paul Albert Gordan.

O desenvolvimento de cálculo nos anos 1700 usado todo o conjunto de números reais sem ter definido-los de forma limpa. A primeira definição rigorosa foi dada por Georg Cantor em 1871 . Em 1874, ele mostrou que o conjunto de todos os números reais é uncountably infinito, mas o conjunto de todos números algébricos é infinito contável. Ao contrário da crença amplamente difundida, seu método não era o seu famoso argumento diagonal, que ele publicou em 1891.

Definição

Construção dos números racionais

Os números reais podem ser construídos como uma conclusão dos números racionais, de tal maneira que uma sequência definida por uma expansão ou decimal binário como {3, 3,1, 3,14, 3,141, 3,1415, ...} converge para um número único verdadeiro. Para mais detalhes e outras construções de números reais, consulte construção de números reais.

Abordagem axiomática

Seja R denotam o um conjunto de números reais. Então:

• O conjunto de R é um campo, o que significa que além e multiplicação são definidos e têm as propriedades habituais.
• O domínio R é ordenada, o que significa que há uma ≥ total da ordem de tal forma que, para todos os números reais x, y e z:
  • se x ≥ y, em seguida, x + z ≥ y + z;
  • se x ≥ 0 e y ≥ 0, em seguida, xy ≥ 0.
• A ordem é Dedekind-completo; isto é, cada não-vazia subconjunto S de R com um limite superior em R tem uma menos ligado (também chamado supremo) superior em R.

A última propriedade é o que diferencia os reais dos racionais . Por exemplo, o conjunto de racionais quadrado com menos do que 2 tem uma racional limite superior (por exemplo, 1,5), mas não menos racional limite superior, porque a raiz quadrada de 2 não é racional.

Os números reais são especificadas de forma única pelas propriedades acima. Mais precisamente, dadas quaisquer dois campos ordenadas Dedekind-completos R ₁ e R _2, existe um campo exclusivo isomorfismo de R ₁ a R _2, o que nos permite pensar neles como essencialmente o mesmo objeto matemático.

Por outro axiomatization de R, ver Axiomatization de Tarski dos reais.

Propriedades

Perfeição

A principal razão para introduzir os reais é que os reais conter todos os limites . Mais tecnicamente, os reais são completo (no sentido de espaços métricos ou espaços uniformes, que é num sentido diferente do que a integralidade Dedekind da ordem na secção anterior). Isto significa o seguinte:

Uma sequência (x _n) de números reais é chamado um Sequência de Cauchy se para qualquer ε> 0 existe um número inteiro N (eventualmente dependendo ε) de tal modo que a distância | x _n - X _m | é menor que ε para todos os n e m, que são ambos maiores do que N. Em outras palavras, é uma sequência de um Seqüência de Cauchy se os seus elementos x _n, eventualmente, vir e permanecer arbitrariamente próximos uns dos outros.

Uma sequência (x _n) converge para o limite de x se para qualquer ε> 0 existe um número inteiro N (eventualmente dependendo ε) de tal modo que a distância | x _n - X | é menor que ε desde que n é maior que N. Em outras palavras, uma seqüência tem limite x se os seus elementos, eventualmente, vir e permanecer arbitrariamente próximo de x.

É fácil de ver que cada sequência convergente é uma seqüência de Cauchy. Um fato importante sobre os números reais é que o inverso também é verdadeiro:

Cada seqüência de números reais Cauchy é convergente.

Ou seja, os reais são completos.

Note que os números racionais não estão completos. Por exemplo, a sequência (1, 1,4, 1,41, 1,414, 1,4142, 1,41421, ...) é de Cauchy, mas não converge para um número racional. (Nos números reais, em contraste, que converge para a raiz quadrada de 2.)

A existência de limites de seqüências de Cauchy é o que faz o cálculo do trabalho e é de grande utilidade prática. O teste padrão numérico para determinar se uma sequência tem um limite é para testar se é uma sequência de Cauchy, como o limite tipicamente não é conhecida de antemão.

Por exemplo, o padrão de série da função exponencial

converge para um número real porque para cada x somas

pode ser feita arbitrariamente pequena, escolhendo N suficientemente grande. Isso prova que a seqüência é Cauchy, por isso sabemos que a sequência converge mesmo que o limite não é conhecido antecipadamente.

"O campo ordenado completo"

Os números reais são muitas vezes descrito como "o campo completo ordenada", uma frase que pode ser interpretada de várias maneiras.

Em primeiro lugar, um pedido pode ser treliça-completo. É fácil ver que nenhum campo encomendado pode ser reticulado-complete, porque ele não pode ter nenhum elemento maior (dado qualquer elemento z, z + 1 for maior), de modo que este não é o sentido que se destina.

Além disso, uma ordem pode ser Dedekind-completo, tal como definido nas Axiomas de seção. O resultado singularidade no final da seção que justifica o uso da palavra "o" "campo completo ordenou" na frase quando este é o sentido de "completo" que se destina. Este sentimento de completude é mais estreitamente relacionado com a construção dos reais de cortes de Dedekind, uma vez que a construção começa a partir de um campo ordenado (os racionais) e, em seguida, forma o Dedekind-conclusão de que de uma forma padrão.

Estas duas noções de integralidade ignorar a estrutura do campo. No entanto, uma grupo pedidos (neste caso, o grupo de aditivos do campo) define um estrutura uniforme, e estruturas uniformes têm uma noção de completude (topologia); a descrição na seção acima Integralidade é um caso especial. (Referimo-nos à noção de integralidade em espaços uniformes, em vez de a noção relacionada e mais conhecido por espaços métricos, uma vez que a definição de espaço métrico depende de já ter uma caracterização dos números reais.) Não é verdade que R é o campo encomendado apenas uniforme completo, mas é a única maneira uniforme completo Campo de Arquimedes, e de fato um frequentemente ouve a frase "campo de Arquimedes completa" em vez de "Complete campo ordenou". Uma vez que pode ser provado que qualquer campo de Arquimedes uniforme completo também deve ser Dedekind-completo (e vice-versa, é claro), este justifica usando "a" na frase "o campo de Arquimedes completa". Este sentimento de completude é mais estreitamente relacionado com a construção dos reais de seqüências de Cauchy (a construção realizadas no pleno neste artigo), uma vez que ele começa com um campo de Arquimedes (os racionais) e constitui a conclusão uniforme do mesmo em um padrão caminho.

Mas o uso original da frase "campo de Arquimedes completa" era por David Hilbert , que ainda queria dizer outra coisa por ela. Ele quis dizer que os números reais formam o maior campo de Arquimedes no sentido de que todos os outros campos de Arquimedes é um subcampo de R. Assim, R é "completa" no sentido de que nada mais pode ser adicionado a ele sem fazer com que já não é um campo de Arquimedes. Este sentimento de completude é mais estreitamente relacionado com a construção dos reais de números surreais, desde que a construção começa com uma classe própria que contém todos os campos solicitados (os surreals) e, em seguida, seleciona a partir dele o maior subcampo de Arquimedes.

Propriedades avançadas

Os reais são incontável; ou seja, há um número estritamente mais real do que números naturais , mesmo que ambos os conjuntos são infinitos . Na verdade, o cardinalidade dos reais é igual ao do conjunto de subconjuntos dos números naturais, e Argumento diagonal de Cantor afirma que cardinalidade deste último conjunto é estritamente maior do que a cardinalidade de N. Uma vez que apenas um conjunto contável de números reais podem ser algébrica, quase todos os números reais são transcendental. A não existência de um subconjunto dos reais com cardinalidade estritamente entre a dos números inteiros e os reais é conhecido como o hipótese do contínuo. A hipótese do contínuo não pode nem ser provada nem ser refutada; é independente dos axiomas da teoria dos conjuntos .

Os números reais formar um espaço métrica: a distância entre x e y é definido como sendo o valor absoluto | x - y |. Em virtude de ser um totalmente ordenado conjunto, eles também carregam uma ordem topologia; a topologia decorrente da métrica e o resultante de uma ordem são idênticos. Os reais são um contraível (daqui e ligado simplesmente conexa), espaço métrico separável do 1 dimensão, e são em toda parte densa. Os números reais são localmente compacto, mas não compacta . Existem várias propriedades que especificam-lhes excepcionalmente; por exemplo, todos sem limites, conectado, e separável topologias ordem são necessariamente homeomorphic para os reais.

Cada número real não negativo tem uma raiz quadrada em R, e nenhum número negativo faz. Isto mostra que a ordem de I é determinada pela sua estrutura algébrica. Além disso, cada polinômio de grau ímpar admite pelo menos uma raiz: estas duas propriedades fazem R o exemplo de um premier verdadeiro campo fechado. Provando esta é a primeira metade de uma prova da teorema fundamental da álgebra.

Os reais levar um canônica medir, a Lebesgue medida, que é o Haar medida sobre a sua estrutura como um grupo topológico normalizado de modo a que o intervalo unitário [0,1] tem medida 1.

O axioma supremo dos reais refere-se a subconjuntos dos reais e, portanto, uma declaração lógica de segunda ordem. Não é possível caracterizar os reais com primeira ordem lógica sozinho: o Löwenheim-Skolem teorema implica que existe um subconjunto denso contável dos números reais satisfazem exatamente as mesmas frases em lógica de primeira ordem como os próprios números reais. O conjunto de números hiperreais satisfaz as mesmas sentenças de primeira ordem como R. Campos ordenados que satisfaçam as mesmas sentenças de primeira ordem como R são chamados modelos invulgares de R. Isso é o que faz trabalho de análise fora do padrão; provando uma declaração de primeira ordem em algum modelo diferente do padrão (que pode ser mais fácil do que provar isso em R), sabemos que a mesma declaração também deve ser verdade de R.

Generalizações e extensões

Os números reais podem ser generalizados e ampliado em várias direções diferentes:

• Os números complexos conter soluções para todos os polinomiais equações e, portanto, são uma corpo algebricamente fechado, ao contrário dos números reais. No entanto, os números complexos não são um campo ordenada.
• O sistema de número real affinely estendida acrescenta dois elementos + ∞ e -∞. É um espaço compacto . Não é mais um campo, nem mesmo um grupo de aditivos; ainda tem um ordem total; Além disso, é um completa estrutura.
• O verdadeira linha projetiva acrescenta apenas um valor ∞. É também um espaço compacto. Mais uma vez, já não é um domínio, nem mesmo um grupo de aditivos. No entanto, isso permite a divisão de um elemento diferente de zero por zero. Ele não é mais ordenada.
• O linha real de longo cola juntos ℵ ₁ * + ℵ ₁ cópias da linha real mais um único ponto (aqui ℵ ₁ * denota a ordem invertida de ℵ ₁₎ para criar um conjunto ordenado que é "localmente" idênticos aos números reais, mas de algum modo mais longo; por exemplo, há uma incorporação de preservação da ordem de ℵ ₁ na linha real de longo, mas não nos números reais. A linha real de longo é o maior conjunto ordenado que é archimedean completo e localmente. Tal como acontece com os dois exemplos anteriores, este conjunto não é um campo ou aditivo grupo.
• Encomendados campos que se estendem os reais são o números hiperreais eo números surreais; ambos contêm números infinitesimais e infinitamente grandes e, portanto, não são Arquimedes.
• Operadores auto-adjuntos em um Espaço de Hilbert (por exemplo, complexos quadrados auto-adjuntos matrizes ) generalizar os reais em muitos aspectos: eles podem ser encomendados (embora não totalmente ordenado), eles estão completos, todos os seus valores próprios são reais e eles formam um verdadeiro álgebra associativa. Operadores definida positiva correspondem às reais positivos e operadores normais correspondem aos números complexos.

"reais" na teoria dos conjuntos

Na teoria dos conjuntos , especificamente teoria dos conjuntos descritivo o Baire espaço é utilizado como um substituto para os números reais uma vez que o último tem algumas propriedades topológicos (conexidade) que são um inconveniente técnico. Elementos de espaço de Baire são referidos como "reais".