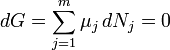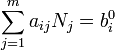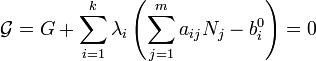Equilíbrio químico
Fundo para as escolas Wikipédia
Esta seleção wikipedia foi escolhido por voluntários que ajudam Crianças SOS da Wikipedia para este Seleção Wikipedia para as escolas. SOS Children trabalha em 45 países africanos; você pode ajudar uma criança em África ?
Em um processo químico, equilíbrio químico é o estado em que o atividades químicas ou As concentrações dos reagentes e produtos não têm qualquer alteração líquida ao longo do tempo. Normalmente, este seria o estado que resulta quando a frente processo químico prossegue na mesma taxa como o seu reacção inversa. As taxas de reação da frente e reverter reações geralmente não são zero, mas, sendo igual, não há mudanças líquidas em qualquer das concentrações dos reagentes ou produtos. Este processo é chamado equilíbrio dinâmico
| |||||
Introdução

Em uma reacção química , quando os reagentes são misturados em conjunto num recipiente de reacção (e aqueceu-se, se necessário), o conjunto de reagentes não são convertidos nos produtos. Depois de algum tempo (que pode ser mais curto do que milionésimos de segundo ou mais do que a idade do universo), vai chegar um ponto em que uma quantia fixa de reagentes vai existir em harmonia com uma quantidade fixa de produtos, as quantidades de nenhuma mudança anymore. Isto é chamado de equilíbrio químico.
O conceito de equilíbrio químico foi desenvolvido depois Berthollet (1803) constatou que algumas reações químicas são reversível. Para qualquer reacção, tal como
estar em equilíbrio as taxas das reacções para a frente e para trás (reverso) tem que ser igual. Neste equação química com setas apontando para os dois lados arpão para indicar equilíbrio, A e B são reagente espécie química, S e T são espécies de produtos, e α, β, σ, e τ são o coeficientes estequiométricas dos respectivos reagentes e produtos. A posição de equilíbrio de uma reação é dito para mentir mais para a direita, se, em equilíbrio, quase todos os reagentes são usados para cima e longe para a esquerda se quase nenhum produto é formado a partir dos reagentes.
Guldberg e Waage (1865), com base em ideias de Berthollet, propuseram a lei de ação de massas:
onde A, B, S e T são, massas activas e k + e K - são constantes de velocidade. Uma vez que as taxas de trás para a frente e são iguais:
e a razão entre as constantes de velocidade é também uma constante, conhecido agora como um constante de equilíbrio.
Por convenção os produtos formam o numerador . No entanto, o lei da ação das massas é válida apenas para concertadas reações de uma etapa que procedem através de um único transição de estado e não é válida em geral, porque equações de taxa não, em geral, seguir o estequiometria da reacção como Guldberg e Waage tinha proposto (ver, por exemplo, a substituição nucleofílica alifática por SN1 ou reacção de hidrogénio e bromo , para formar brometo de hidrogénio). Igualdade de frente e taxas de reação para trás, no entanto, é uma condição necessária para o equilíbrio químico, embora não seja suficiente para explicar porque ocorre equilíbrio.
Apesar do fracasso dessa derivação, a constante de equilíbrio para a reacção é de facto uma constante, independente das actividades das diferentes espécies envolvidas, embora isso não depende da temperatura, como observado pela t equação Hoff van '. A adição de um catalisador irá afectar tanto a reacção para a frente e a reacção inversa da mesma forma e não terá um efeito sobre a constante de equilíbrio. O catalisador irá acelerar ambas as reacções, aumentando assim a velocidade à qual o equilíbrio é atingido.
Embora as concentrações de equilíbrio macroscópicas são constante no tempo reacções ocorrem ao nível molecular. Por exemplo, no caso do ácido etanóico dissolvido em água e formando ethanoate e iões hidrónio,
- CH 3 CO 2 H + H2O ⇌ CH 3 CO 2 - + H3O +
um protão pode saltar de uma molécula de ácido etanóico em que uma molécula de água e, em seguida, para um ião de etanoato de modo a formar uma outra molécula de ácido etanóico e deixando o número de moléculas de ácido etanóico inalterada. Este é um exemplo de equilíbrio dinâmico. Equilíbrios, como o resto da termodinâmica, são fenómenos estatísticos, médias de comportamento microscópico.
Princípio de Le Chatelier (1884) é um princípio útil que dá uma ideia qualitativa da resposta de um sistema de equilíbrio a mudanças nas condições de reacção. Se um equilíbrio dinâmico é perturbado pela alteração das condições, da posição de equilíbrio desloca-se para neutralizar a mudança. Por exemplo, a adição de mais S do lado de fora vai fazer com que um excesso de produtos, e o sistema vai tentar contrariar isso aumentando a reacção inversa e empurrando o ponto de equilíbrio para trás (embora a constante de equilíbrio permanecerá o mesmo).
Se ácido mineral seja adicionado à mistura de ácido etanóico, o aumento da concentração do ião hidrónio, a quantidade de dissociação deverá diminuir à medida que a reacção é impulsionada para a esquerda, de acordo com este princípio. Isto também pode ser deduzida a partir da expressão constante de equilíbrio para a reacção:
Se {H 3 O +} {aumenta CH 3 CO 2 H} deve aumentar e {CH 3 CO 2 -} deve diminuir.
A versão quantitativa é dada pela quociente reacção.
JW Gibbs sugeriu em 1873 que o equilíbrio é atingido quando o Gibbs energia do sistema está no seu valor mínimo (assumindo que a reacção é realizada sob uma pressão constante). O que isto significa é que o derivado da energia de Gibbs que diz respeito aos coordenar reacção (uma medida da extensão da reacção que tenha ocorrido, que varia de zero para todos os reagentes para uma máxima para todos os produtos) desaparece, uma sinalização ponto estacionário. Este derivado é geralmente chamado, por determinadas razões técnicas, a mudança de energia Gibbs. Este critério é necessário e suficiente. Se uma mistura não está em equilíbrio, a libertação do excesso de energia de Gibbs (ou Helmholtz energia em reacções de volume constante) é a "força motriz" para a composição da mistura para alterar até que o equilíbrio é atingido. A constante de equilíbrio pode ser relacionado com o padrão de energia de Gibbs para a reacção de mudança pela equação
em que R é a constante universal dos gases e T a temperatura .
Quando os reagentes estão dissolvidos num meio de alta força iónica o quociente entre coeficientes de atividade pode ser considerado constante. Nesse caso, o quociente de concentração, K c,
onde [A] é a concentração de A, etc, é independente do analítico da concentração dos reagentes. Por esta razão, as constantes de equilíbrio para soluções são geralmente determinada em meios de força iónica elevada. K c varia com a força iónica, temperatura e pressão (ou volume). Da mesma forma, para os gases K P depende pressão parcial. Essas constantes são mais fáceis de medir e encontrou em cursos de química do ensino médio.
Termodinâmica
A relação entre a energia de Gibbs e a constante de equilíbrio pode ser encontrada considerando potenciais químicos. A termodinâmica condição para o equilíbrio químico é
- Em constante pressão ΔG = 0 (ΔG é a mudança Gibbs energia livre para a reação)
- No Aa volume constante = 0 (Aa representa a mudança no Energia livre de Helmholtz para a reação)
Neste artigo apenas o caso de pressão constante é considerada. O caso volume constante é importante na geoquímica e química da atmosfera onde as variações de pressão são significativos. Note-se que, se os reagentes e os produtos foram em estado padrão (completamente puro), então não haveria reversibilidade e não equilíbrio. A mistura dos produtos e reagentes contribui com uma grande entropia (conhecido como entropia de mistura) para os estados que contêm igual mistura de produtos e reagentes. A combinação do padrão de variação de energia de Gibbs e a energia de Gibbs da mistura determina o estado de equilíbrio.
Em geral, um sistema de equilíbrio é definida por uma equação de equilíbrio escrevendo para a reacção
A fim de satisfazer a condição de equilíbrio termodinâmico, a energia de Gibbs deve ser estacionário, o que significa que o derivado de L em relação ao coordenar reacção (ΔG) deve ser zero. Pode ser mostrado que ΔG é, de facto, igual à diferença entre o potenciais químicas dos produtos e os dos reagentes. Por conseguinte, a soma das energias de Gibbs dos reagentes deve ser igual à soma das energias de Gibbs dos produtos.
onde μ é neste caso um molar parcial da energia de Gibbs, uma potencial químico. O potencial químico de um reagente A é uma função do actividade, {A} desse reagente.
Substituindo expressões como esta na equação de energia Gibbs :
à pressão e temperatura constante torna-se:
resulta em:
Ao substituir os potenciais químicos:
o relacionamento torna-se:
No equilíbrio 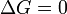 e, por conseguinte,
e, por conseguinte,
levando a:
ΔG m ó representa a variação da energia de Gibbs molar padrão para a reacção e K é a constante de equilíbrio. Note-se que as atividades e constantes de equilíbrio são números adimensionais.
Tratamento de actividade
A expressão para a constante de equilíbrio pode ser re-escrita como o produto de um quociente de concentração, e K c uma coeficiente de actividade quociente, Γ.
[A] é a concentração de reagente A, etc. É possível, em princípio, para se obter os valores dos coeficientes de actividade, γ. Para as soluções, tais como equations o Pode ser usado equação de Debye-Hückel ou extensões como equação Davies ou equações Pitzer. Software (abaixo). No entanto, isto nem sempre é possível. É prática comum para supor que Γ é uma constante, e a utilizar o quociente entre a concentração no local da constante de equilíbrio termodinâmico. Também é prática geral utilizar o termo equilíbrio constante, em vez de o quociente entre a concentração mais precisa. Esta prática será seguido aqui.
Para as reacções em fase gasosa pressão parcial é utilizado no lugar de concentração e coeficiente de fugacidade no lugar do coeficiente de atividade. No mundo real, por exemplo, ao fazer amoníaco na indústria, os coeficientes de fugacidade deve ser tida em conta. Fugacidade, f, é o produto da pressão parcial e coeficiente de fugacidade. O potencial de uma espécie química na fase gasosa é determinado pela
Portanto, a expressão geral que define uma constante de equilíbrio é válido para as duas fases da solução e gás.
A justificação para a utilização de quocientes de concentração
Na solução aquosa, as constantes de equilíbrio são geralmente determinada na presença de um electrólito "inerte" tal como nitrato de sódio 3 ou NaNO Perclorato de potássio KClO 4. O força iónica, Eu, de uma solução contendo um sal dissolvido, X + Y -, é dada pela
onde c representa a concentração, z significa carga iônica ea soma é tomada sobre todas as espécies em equilíbrio. Quando a concentração de sal dissolvido é muito mais elevada do que as concentrações dos reagentes analíticos, a força iónica é efectivamente constante. Uma vez que coeficientes de actividade depende da força iónica os coeficientes das espécies de actividade são efectivamente independente da concentração. Assim, a suposição de que Γ é constante é justificada. O quociente de concentração simples é um múltiplo de a constante de equilíbrio.
No entanto, K c irá variar com a força iónica. Se é medida a uma série de diferentes forças iónicas o valor pode ser extrapolada a zero a força iónica. O quociente de concentração obtido desta maneira é conhecida, paradoxalmente, como uma constante de equilíbrio termodinâmico.
Para usar um valor publicado de uma constante de equilíbrio em condições de força iónica diferentes das condições utilizadas na sua determinação, o valor deve ser ajustado de Software (abaixo).
Misturas metastáveis
Uma mistura pode ser parecem não ter tendência para mudar, no entanto, não está em equilíbrio. Por exemplo, uma mistura de SO 2 e O 2 é metaestável que haja uma barreira cinética de formação do produto, SO 3.
- 2SO 2 + O 2
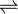 2SO 3
2SO 3
A barreira pode ser ultrapassada quando um catalisador está também presente na mistura como na Processo de contato, mas o catalisador não afeta as concentrações de equilíbrio.
Da mesma forma, a formação de bicarbonato de dióxido de carbono e água é muito lenta em condições normais
- CO 2 + 2H 2 O
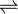 HCO 3 - + H3O +
HCO 3 - + H3O +
mas quase instantâneo na presença do catalisador enzima anidrase carbônica.
Compostos puros em equilíbrios
Quando substâncias puras (líquidos ou sólidos) estão envolvidos em equilíbrios eles não aparecem na equação de equilíbrio
Aplicando a fórmula geral de uma constante de equilíbrio para o caso específico de um ácido etanóico obtém
Pode supor-se que a concentração de água é constante. Esta hipótese será soluções válidas para todos, mas muito concentrados. A expressão constante de equilíbrio é, portanto, geralmente escrito como
Onde agora
![K = * K_c [H_2O] \,](../../images/117/11727.png)
um factor constante é incorporado na constante de equilíbrio.
Um caso particular é o auto-ionização de água própria
A constante de auto-ionização de água é definida como
![K_w = [H ^ +] [OH ^ -] \,](../../images/117/11729.png)
É perfeitamente legítimo para escrever [H +] para a concentração de iões de hidrônio, uma vez que o estado de solvatação do protão é constante (em soluções diluídas) e assim não afecta as concentrações de equilíbrio. K w varia com a variação de força e / ou a temperatura iónico.
As concentrações de H + e OH - não são quantidades independentes. Mais comumente [OH -] é substituído pelo K w [H +] -1 em expressões constantes de equilíbrio que de outra forma hidróxido .
Sólidos também não aparecem na equação de equilíbrio. Um exemplo é a Reação Boudouard:
para os quais a equação (sem carbono sólido) é escrita como:
Múltiplos equilíbrios
Considere o caso de um ácido dibásico H 2 A. Quando dissolvido em água, a mistura conterá H 2 A, HA - e A 2. Este equilíbrio pode ser dividido em duas etapas, em cada uma das quais é um protão libertado.
K 1 e K 2 são exemplos de constantes de equilíbrio escalonadas. A constante de equilíbrio geral, 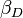 , É produto das constantes escalonadas.
, É produto das constantes escalonadas.
Note-se que estes são constantes constantes de dissociação porque os produtos do lado direito da expressão de equilíbrio são produtos de dissociação. Em muitos sistemas, é preferível utilizar as constantes de associação.
β 1 e β 2 são exemplos de constantes de associação. Claramente β 1 = 1 / K 2 e β 2 = 1 / β D; lg β 1 = pK 2 e LG β 2 = pKa + 2 pK 1
Efeito da variação de temperatura sobre uma constante de equilíbrio
O efeito da alteração da temperatura sobre uma constante de equilíbrio é dada pela t equação Hoff van '
Assim, por reacções exotérmicas, (AH é negativo) K diminui com a temperatura, mas, para reacções endotérmicas, (AH é positivo) k aumenta com a temperatura. Uma formulação alternativa é
À primeira vista, isto parece oferecer um meio de obter a entalpia molar padrão da reacção através do estudo da variação de K com a temperatura. Na prática, no entanto, o método não é fiável, porque a propagação do erro quase sempre dá muito grandes erros nos valores calculados deste modo.
Tipos de equilíbrio e algumas aplicações
- Na fase gasosa. Motores de foguete
- A síntese industrial, tais como amónia na Processo Haber-Bosch (retratado à direita) tem lugar através de uma sucessão de passos de equilíbrio, incluindo processos de adsorção.
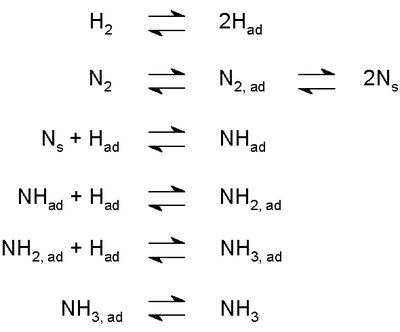
- química atmosférica
- A água do mar e outras águas naturais: Oceanografia química
- Distribuição entre duas fases
- Coeficiente logD-Distribuição: Importante para produtos farmacêuticos onde lipofilicidade é uma propriedade significativa de uma droga
- Extracção líquido-líquido, Troca iónica, cromatografia
- Produto de solubilidade
- Absorção e liberação de oxigênio por hemoglobina no sangue
- Equilíbrio ácido / base: A constante de dissociação de ácido, hidrólise, soluções tampão, indicadores, homeostase ácido-base
- Complexação de metal-ligando: agentes sequestrantes, terapia de quelação, Reagentes de contraste de MRI, Equilíbrio Schlenk
- Formação de aducto: Química Host-hóspede, química supramolecular, reconhecimento molecular, tetróxido
- Em certos reacções oscilantes, a abordagem de equilíbrio não é assintoticamente mas sob a forma de uma oscilação amortecida.
- O relacionada Equação de Nernst em electroquímica dá a diferença de potencial do eléctrodo como uma função de concentrações redox.
- Quando as moléculas em cada lado do equilíbrio são capazes de reagir irreversivelmente ainda em reacções secundárias, a proporção do produto final é determinada de acordo com o Curtin-Hammett princípio.
Nestas aplicações, os termos tais como a estabilidade constante, constante de formação, constante de ligação, constante de afinidade, a associação / dissociação constante são usadas. Na bioquímica, é comum para dar unidades para as constantes de ligação, que servem para definir as unidades de concentração utilizados quando o valor da constante foi determinada.
Composição de uma mistura em equilíbrio
Quando o único equilíbrio é o da formação de uma mistura 1: 1 de aduto como a composição de uma mistura, há um número qualquer de maneiras que a composição de uma mistura pode ser calculada. Por exemplo, veja Tabela ICE para um método tradicional de cálculo do pH de uma solução de um ácido fraco.
Existem três abordagens para o cálculo geral da composição de uma mistura em equilíbrio.
- A abordagem mais simples é manipular as diversas constantes de equilíbrio até que as concentrações desejadas são expressas em termos de constantes de equilíbrio de medição (equivalente a medição de potenciais químicos) e condições iniciais.
- Minimizar a energia de Gibbs do sistema.
- Satisfazem a equação de balanço de massa. As equações de balanço de massa são simplesmente declarações que demonstram que a concentração total de cada reagente deve ser constante pela lei do conservação de massa.
Resolver as equações de balanço de massas
Em geral, os cálculos são bastante complicado. Por exemplo, no caso de um ácido dibásico, H 2 A dissolvido em água dos dois reagentes pode ser especificado como o base conjugada, um grupo 2-, eo protões, H +. As seguintes equações de balanço de massa, pode aplicar-se igualmente bem a uma base, tal como 1,2-diaminoetano, caso em que a própria base é designado como o reagente A:
Com T A concentração total de espécies A. Note que é costume omitir as cargas iônicas ao escrever e utilizar estas equações.
Quando as constantes de equilíbrio são conhecidos e as concentrações dadas são especificados existem duas equações em duas concentrações "livres" desconhecidos [A] e [H]. Isso decorre do fato de que [HA] = β 1 [A] [H], [H 2 A] = β 2 [A] [H] e 2 [OH] = K w [H] -1
de modo que as concentrações dos "complexos" são calculados a partir das concentrações livres e as constantes de equilíbrio. Expressões gerais aplicáveis a todos os sistemas com dois reagentes, A e B seria
É fácil ver como isto pode ser aumentado para três ou mais reagentes.
Composição de ácidos polibásicos como uma função do pH
A composição das soluções contendo reagentes A e H é fácil de calcular, em função de p [H]. Quando [H] é conhecido, a concentração livre [A] é calculado a partir da equação de equilíbrio de massa em A. Aqui é um exemplo dos resultados que podem ser obtidos.
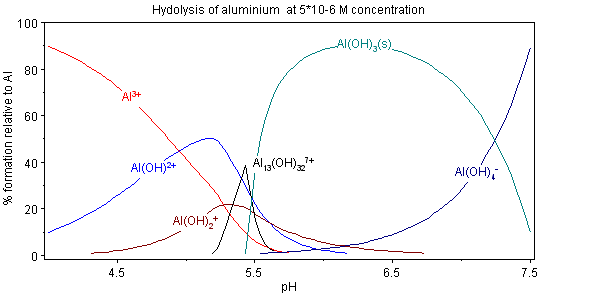
Este diagrama, para a hidrólise do alumínio O ácido de Lewis Al 3+ aq mostra as concentrações das espécies para uma solução 5 M x 10 -6 de um sal de alumínio como uma função do pH. Cada concentração é apresentada como uma percentagem do total de alumínio.
Equilíbrios solução com precipitação
O diagrama acima ilustra o ponto de que um precipitar que não é uma das principais espécies na solução de equilíbrio pode ser formado. A pH 5,5, logo abaixo as principais espécies presentes em uma solução 5 � de Al 3+ são hidróxidos de alumínio Al (OH) 2+, Al (OH) 2 + Al e 13 (OH) 32 7 +, mas no aumento do pH Al (OH) 3 precipita a partir da solução. Isto ocorre porque o Al (OH) 3 tem uma muito grande energia de rede. À medida que o pH aumenta mais e mais Al (OH) 3 sai da solução. Este é um exemplo de Princípio de Le Chatelier em acção: O aumento da concentração do ião hidróxido faz com que mais hidróxido de alumínio para precipitar, o que remove hidróxido a partir da solução. Quando a concentração de hidróxido torna-se suficientemente elevada do aluminato solúvel, Al (OH) 4 -, é formado.
Outro exemplo comum onde ocorre quando a precipitação é um catião de metal interage com um ligando aniónico para formar um complexo electricamente neutro. Se o complexo é hydrophopbic, ele vai precipitar para fora da água. Isto ocorre com o níquel de iões de Ni2 + e dimetilglioxima, (dmgH 2): neste caso, a energia de rede do sólido não é particularmente grande, mas é muito superior ao de energia solvatação da molécula de Ni (dmgH) 2.
Minimização da energia de Gibbs
Em equilíbrio, G é no mínimo:
Para um sistema fechado, sem partículas pode entrar ou sair, embora possam ser combinados de várias maneiras. O número total de átomos de cada elemento irá permanecer constante. Isto significa que a minimização acima deve ser submetido às restrições:
onde 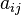 é o número de átomos do elemento em j i b i molécula e 0 é o número total de átomos do elemento i, que é uma constante, uma vez que o sistema é fechado. Se existem um total de k tipos de átomos no sistema, então haverá k tais equações.
é o número de átomos do elemento em j i b i molécula e 0 é o número total de átomos do elemento i, que é uma constante, uma vez que o sistema é fechado. Se existem um total de k tipos de átomos no sistema, então haverá k tais equações.
Este é um problema padrão em optimização, como conhecido minimização restrita. O método mais comum de resolver-se usando o método de Multiplicadores de Lagrange, também conhecido como multiplicadores indeterminados (embora possam ser utilizados outros métodos).
Definir:
onde o 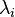 são os multiplicadores de Lagrange, um para cada elemento. Isto permite que cada um dos
são os multiplicadores de Lagrange, um para cada elemento. Isto permite que cada um dos 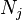 a ser tratado de forma independente, e pode ser demonstrado utilizando as ferramentas de cálculo multivariada que a condição de equilíbrio é dada pela
a ser tratado de forma independente, e pode ser demonstrado utilizando as ferramentas de cálculo multivariada que a condição de equilíbrio é dada pela
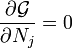 e
e 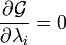
(Para ver a prova Multiplicadores de Lagrange)
Este é um conjunto de equações em incógnitas (m + k) (m + k) (a 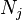 e o
e o 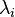 ) E podem, portanto, ser resolvidos para as concentrações de equilíbrio
) E podem, portanto, ser resolvidos para as concentrações de equilíbrio 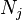 contanto que os potenciais químicos são conhecidas como funções das concentrações à temperatura e pressão dadas. (Ver Bases de dados termodinâmicos para substâncias puras).
contanto que os potenciais químicos são conhecidas como funções das concentrações à temperatura e pressão dadas. (Ver Bases de dados termodinâmicos para substâncias puras).
Este método para calcular as concentrações de equilíbrio químico é útil para sistemas com um grande número de moléculas diferentes. A utilização de equações de conservação k atómicas para o elemento de restrição de massa é simples, e substitui o uso das equações estequiométricas de coeficientes.
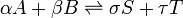
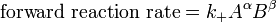
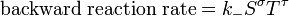
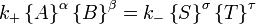
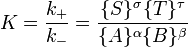
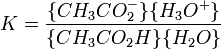
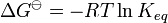
![K_c = \ frac {[S] ^ \ sigma [T] ^ \ tau} {[A] ^ \ alpha [B] ^ \ beta}](../../images/117/11709.png)
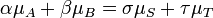
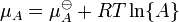
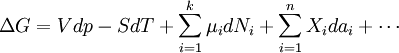
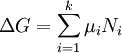

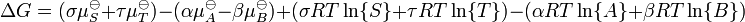
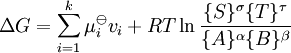
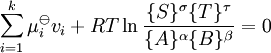
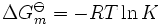
![K = \ frac {{[S]} ^ \ sigma {[T]} ^ \ tau ...} {{[A]} ^ \ alpha {[B]} ^ \ beta ...} \ times \ frac {{\ gamma_S} ^ \ sigma {\ gamma_T} ^ \ tau ...} {{\ gamma_A} ^ \ alpha {\ gamma_B} ^ \ beta ...} = K_c \ Gamma](../../images/117/11719.png)
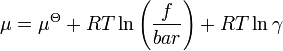
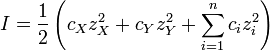
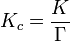
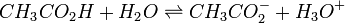
![K_c = \ frac {[{} CH_3CO_2 ^ -] [{H_3O} ^ +]} {[{} CH_3CO_2H] [{H_2O}]}](../../images/117/11725.png)
![K = \ frac {[{} CH_3CO_2 ^ -] [{H_3O} ^ +]} {[{CH_3CO_2H}]}](../../images/117/11726.png)
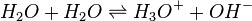
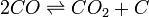
![K_c = \ frac {[CO_2]} {[CO] ^ 2}](../../images/117/11731.png)
![H_2A \ rightleftharpoons HA ^ - ^ + H +: K_1 = \ frac {[HA ^ -] [H ^ +]} {[H_2A]}](../../images/117/11732.png)
![HA ^ - \ rightleftharpoons A ^ {2} + H ^ +: k_2 = \ frac {[A ^ {2 -}] [H ^ +]} {[HA ^ -]}](../../images/117/11733.png)
![H_2A \ rightleftharpoons A ^ {2} + 2H ^ +: \ beta_D = \ frac {[A ^ {2 -}] [H ^ +] ^ 2} {[H_2A]} = K_1K_2](../../images/117/11735.png)
![A ^ {2} + H ^ + \ rightleftharpoons HA ^ -: \ beta_1 = \ frac {[HA ^ -]} {[A ^ {2 -}] [H ^ +]}](../../images/117/11736.png)
![A ^ {2} + 2H ^ + \ rightleftharpoons H_2A: \ beta_2 = \ frac {[H_2A]} {[A ^ {2 -}] [H ^ +] ^ 2}](../../images/117/11737.png)
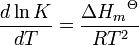
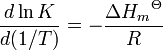
![T_A = [A] + [HA] + [H_2A] \,](../../images/117/11744.png)
![T_H = [H] + [HA] + 2 [H_2A] - [OH] \,](../../images/117/11745.png)
![T_A = [A] + \ beta_1 [A] [H] + \ beta_2 [A] [H] ^ 2 \,](../../images/117/11746.png)
![T_H = [H] + \ beta_1 [A] [H] + 2 \ beta_2 [A] [H] ^ 2 - K_w [H] ^ {- 1} \,](../../images/117/11747.png)
![T_A = [A] + \ sum_i {p_i \ beta_i [A] ^ {} p_i [B] ^ {}} q_i](../../images/117/11748.png)
![T_B = [B] + \ sum_i {q_i \ beta_i [A] ^ {} p_i [B] ^ {}} q_i](../../images/117/11749.png)