Espaço compacto

Em matemática , um subconjunto do espaço euclidiano R ⁿ é chamado compacto se é e fechado delimitada. Por exemplo, em I, o fechada intervalo unitário [0, 1] é compacto, mas o conjunto de números inteiros Z não é (não é limitado) e nem é o intervalo semi-aberto [0, 1) (não é fechado).

Uma abordagem mais moderna é chamar um topológico espaço compacto se cada um dos seus tampas abertas tem uma subcobertura finita. O Heine-Borel teorema mostra que esta definição é equivalente a "fechado e limitado" para subconjuntos do espaço euclidiano.

Nota: Alguns autores como Bourbaki usar o termo "quase-compacto" em vez disso, e reservar o termo "compacto" para espaços topológicos que são Hausdorff e "quasi-compacto". Um único conjunto compacto é por vezes referido como um compactum; na sequência da Latina segunda declinação (neutro), a forma plural correspondente é compacta.

História e motivação

O termo compacto foi introduzido por Frechet em 1906 .

Há muito tem sido reconhecido que uma propriedade como compacidade é necessário provar muitos teoremas úteis. Ela costumava ser que "compacto" significava "sequencialmente compacto" (cada seqüência tem uma subseqüência convergente). Foi quando principalmente Foram estudados espaços métricos. A definição "cobrindo compacto" tornou-se mais proeminente porque nos permite considerar espaços topológicos gerais, e muitos dos antigos resultados sobre espaços métricos podem ser generalizados para esta definição. Esta generalização é particularmente útil no estudo de espaços funcionais, muitos dos quais não são espaços métricos.

Uma das principais razões para estudar espaços compactos é porque eles são de certa forma muito semelhante à conjuntos finitos: há muitos resultados que são fáceis de mostrar para conjuntos finitos, cujas provas transitar com alteração mínima para espaços compactos. Diz-se frequentemente que "compacidade é a próxima melhor coisa a finitude". Aqui está um exemplo:

• Suponhamos que o símbolo X representa um Espaço Hausdorff, e nós temos um ponto x em X e um subconjunto finito A do X que não contenham x. Então nós podemos x separada e um por bairros: para cada um em um, deixe-U (x) e V (a) ser vizinhanças disjuntas que contenham x e um, respectivamente. Em seguida, a intersecção de todos os U (x) e a união de toda a V (a) são os bairros necessários de x e A.

Observe que, se A é infinito, a prova falhar, porque a interseção de arbitrariamente muitos bairros de x pode não ser um bairro de x. A prova pode ser "resgatado", no entanto, se A é compacto: nós simplesmente tomar uma subcobertura finita da cobertura {V (a)} de A. Desta forma, vemos que em um espaço de Hausdorff, qualquer ponto pode ser separada por bairros a partir de qualquer conjunto compacto não o contém. Na verdade, repetindo o argumento mostra que quaisquer dois conjuntos compactos disjuntos em um espaço de Hausdorff pode ser separada por bairros - note que este é precisamente o que teremos se substituir "ponto" (ou seja, singleton conjunto) com o "conjunto compacto" no Hausdorff axioma de separação. Muitos dos argumentos e resultados que envolvem espaços compactos seguir esse padrão.

Definições

Compacidade de subconjuntos de R ⁿ

Para qualquer subconjunto do espaço euclidiano R ^n, as quatro condições seguintes são equivalentes:

• Cada tampa aberta tem um finito subcobertura. Esta é a definição mais utilizada.
• Cada sequência no conjunto tem uma subsequência convergente, o ponto limite do que pertence ao conjunto.
• Cada subconjunto infinito do conjunto tem uma ponto de acumulação no conjunto.
• O conjunto é e fechado delimitada. Esta é a condição de que é mais fácil de verificar, por exemplo um fechada intervalo ou fechado n -Ball.

Em outros espaços, estas condições podem ou não ser equivalente, dependendo das propriedades do espaço.

Note-se que enquanto compacidade é uma propriedade do próprio conjunto (com a sua topologia), closedness é relativo a um espaço em que é; acima de "fechada" é usado no sentido de fechado em ^Rn. Um conjunto que é fechado em, por exemplo Q ⁿ normalmente não é fechado em R ^n, portanto, não compacta.

Compacidade de espaços topológicos

A propriedade "subcobertura finita" do parágrafo anterior é mais abstrato do que o "fechado e limitado" um, mas tem a vantagem de que pode ser administrada utilizando a topologia subespaço em um subconjunto de R ^n, eliminando a necessidade de utilização de uma métrica ou um espaço ambiente. Assim, é uma compacidade propriedade topológica. Em certo sentido, o intervalo de unidade fechada [0,1] é intrinsecamente compacto, independentemente de como ele é incorporado em R ou R ^n.

Um espaço topológico X é definido como compacto se todas as suas tampas abertas têm uma subcobertura finita. Formalmente, este significa que

para cada coleção arbitrária subconjuntos de abertas de 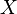tal que , Há um subconjunto finito tal que .

Uma definição equivalente usado muitas vezes é dado em termos da propriedade interseção finita: se toda a coleção de conjuntos fechados satisfazendo a propriedade de interseção finita tem interseção não vazia, então o espaço é compacto. Esta definição é duplo para a habitual expressa em termos de conjuntos abertos.

Alguns autores exigem que um espaço compacto também ser Hausdorff, ea versão não Hausdorff é então chamado quasicompact.

Exemplos de espaços compactos

• Qualquer espaço topológico finito, incluindo o conjunto vazio, é compacto. Ligeiramente mais geralmente, qualquer espaço com um topologia finita (apenas um número finito de conjuntos abertos) é compacto; isto inclui, nomeadamente, a topologia trivial.
• O fechado intervalo unitário é compacto. Isso decorre do Heine-Borel teorema; provando que o teorema é aproximadamente tão duro como uma prova diretamente que é compacto. O intervalo aberto 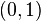não é compacto: o tampa aberta para não tem uma subcobertura finita.
• Para cada número natural n, o n - esfera é compacto. Mais uma vez a partir do teorema de Heine-Borel, a bola de qualquer unidade fechada de dimensão finita espaço vetorial normado é compacto. Isso não é verdade para infinitas dimensões; na verdade, um espaço vetorial normado é finito-dimensional se e somente se o seu bola unidade fechada é compacto.
• O Cantor conjunto é compacto. Uma vez que o p inteiros -adic são homeomorphic ao conjunto de Cantor, eles também formam um conjunto compacto. Desde um conjunto finito contendo elementos p é compacto, isso mostra que o contável produto de conjuntos finitos é compacto, e é, portanto, um caso especial de Teorema de Tychonoff.
• Considere o conjunto de todas as funções a partir da linha número real para o intervalo unidade fechada, e definir uma topologia em de modo a que uma sequência em converge em direcção se e apenas se converge em direcção 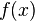para todos . Há apenas uma tal topologia; ele é chamado de topologia de convergência pontual. Em seguida é um espaço topológico compacto, novamente uma conseqüência do teorema de Tychonoff.
• Considere o conjunto de todas as funções satisfazendo a Lipschitz condição para todos e considerar em a métrica induzida pela distância uniforme . Em seguida, pela Ascoli-Arzela teorema do espaço é compacto.
• Qualquer espaço que transporta o topologia cofinite é compacto.
• Qualquer espaço localmente compacto Hausdorff pode ser transformado em um espaço compacto, adicionando um ponto único a ele, por meio de Alexandroff compactification um ponto. O compactification de um ponto de 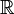é homeomorfo ao círculo 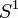; o compactification de um ponto de é homeomorfo à esfera . Usando o compactification de um ponto, também se pode facilmente construir espaços compactos que não são Hausdorff, começando com um espaço não-Hausdorff.
• O espectro de qualquer contínuo operador linear em um Espaço de Hilbert é um subconjunto compacto do número complexo C. Se o espaço de Hilbert é infinito-dimensional, em seguida, qualquer subconjunto compacto de C surge desta forma, que o espectro de um operador linear contínua no espaço de Hilbert.
• O espectro de qualquer anel comutativo ou Álgebra booleana é compacto.
• O Hilbert cubo é compacto.
• O topologia de ordem direita ou topologia de ordem esquerdo de qualquer delimitada conjunto totalmente ordenado é compacto. Em particular, Sierpinski espaço é compacto.
• O espectro principal de qualquer anel comutativo com o Topologia de Zariski é um espaço compacto, importante na geometria algébrica. Estes espectros primos são quase nunca Espaços de Hausdorff.

Teoremas

Alguns teoremas relacionados com compacidade (ver o Glossário topologia para as definições):

• A imagem contínua de um espaço compacto é compacto.
• O teorema do valor extremo: uma função real contínua em um espaço compacto nonempty é limitado e atinge o seu supremo.
• Um subconjunto fechado de um espaço compacto é compacto.
• Um subconjunto de um compacto Espaço Hausdorff é fechado.
• Um subconjunto compacto nonempty dos números reais tem um elemento maior e um elemento menos.
• Um subconjunto de euclidiano n -espaço é compacto se, e somente se ele estiver fechado e limitado. ( Teorema de Heine-Borel)
• A espaço métrico (ou espaço uniforme) é compacto se e só se é e completa totalmente delimitado.
• O produtos de qualquer coleção de espaços compactos é compacto. ( Teorema de Tychonoff, que é equivalente ao axioma de escolha)
• Um espaço compacto de Hausdorff é normal.
• Cada mapa contínuo a partir de um espaço compacto de um espaço de Hausdorff é e fechado adequada. Daí resulta que cada contínua mapa bijective de um espaço compacto de um espaço de Hausdorff é um homeomorfismo .
• Um espaço métrico (ou mais geralmente qualquer primeiro-contável espaço uniforme) é compacto se e somente se cada seqüência no espaço tem uma subseqüência convergente.
• Um espaço topológico é compacto se e somente se todos os líquido sobre o espaço tem uma sub-rede convergente.
• Um espaço topológico é compacto se e somente se todos os filtro no espaço tem um refinamento convergente.
• Um espaço topológico é compacto se e somente se todos os ultrafiltro no espaço é convergente.
• Um espaço topológico pode ser incorporado em um espaço compacto de Hausdorff se e somente se é uma Espaço Tychonoff.
• Cada espaço topológico X é uma subespaço denso de um espaço compacto que tem no máximo um ponto mais do que X. ( Alexandroff um ponto compactification)
• Se o espaço métrico X é compacto e uma tampa aberta do X é dado, então existe um número δ> 0 tal que cada subconjunto de X de diâmetro <δ está contida em algum membro da tampa. ( Número de Lebesgue lema)
• Se um espaço topológico tem uma sub-base de modo a que toda a cobertura do espaço por membros da sub-base tem uma subcobertura finito, então o espaço é compacto. ( Teorema de sub-base de Alexander)
• Dois espaços compactos Hausdorff X ₁ e X ₂ são homeomorphic se e somente se o seu anéis contínuos de funções reais C (X ₁₎ e C (X ₂₎ são isomorphic. ( Teorema de Gelfand-Naimark)

Outras formas de compacidade

Há uma série de propriedades topológicas que são equivalentes a compacidade em espaços métricos, mas são inequivalent em espaços topológicos gerais. Estes incluem o seguinte.

• Sequencialmente compacto: Cada seqüência tem uma subseqüência convergente.
• Countably compacto: Cada tampa aberta contável tem uma subcobertura finita. (Ou, equivalentemente, todo subconjunto infinito possui um ponto de ω-acumulação.)
• Pseudocompact: Toda de valor real contínua função no espaço é limitado.
• Fracamente countably compacto (ou ponto-limite compacto): Cada subconjunto infinito tem um ponto de acumulação.

Enquanto todas estas condições são equivalentes para espaços métricos, em geral, temos as seguintes implicações:

• Espaços compactos são countably compacto.
• Sequencialmente espaços compactos são countably compacto.
• Countably espaços compactos são pseudocompact e fracamente countably compacto.

Nem todo espaço countably compacto é compacto; um exemplo é dado pelo primeiro ordinal incontável com a topologia de ordem. Nem todo espaço compacto é sequencialmente compacto; um exemplo é dado pelo 2 ^[0,1], com a topologia do produto.

Um espaço métrico é chamado de pré-compacto ou totalmente delimitado se qualquer sequência tem uma subsequência de Cauchy; este pode ser generalizada para espaços uniformes. Para espaços métricos completos isto é equivalente a compacidade. Ver relativamente compacto para a versão topológica.

Outra noção relacionada que (por mais definições) é estritamente mais fraca do que é compacidade compacidade local.