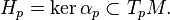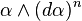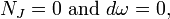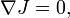Geometria diferencial
Sobre este escolas selecção Wikipedia
Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . SOS Children trabalha em 45 países africanos; você pode ajudar uma criança em África ?
Geometria diferencial é um matemático disciplina que utiliza os métodos de diferencial e integrante cálculo para estudar problemas de geometria . A teoria do plano e no espaço curvas e de superfícies no tridimensional espaço euclidiano formaram a base para o seu desenvolvimento inicial no século XVIII e XIX. Desde o final do século XIX, geometria diferencial cresceu em um campo em questão de modo mais geral, com estruturas geométricas sobre variedades diferenciáveis. Ele está intimamente relacionado com topologia diferencial e com os aspectos geométricos da teoria de equações diferenciais . A prova do Conjectura Poincaré utilizando as técnicas de Fluxo de Ricci demonstrou o poder da abordagem diferencial-geométrica para perguntas em topologia e destacou o importante papel desempenhado pelos métodos analíticos.
Ramos de geometria diferencial
Geometria Riemanniana
Estudos de geometria de Riemann Variedades de Riemann, variedades suaves com uma métrica de Riemannian, uma noção de uma distância expressa por meio de um definida positiva forma bilinear simétrica definida no espaço tangente em cada ponto. Geometria Riemanniana generaliza a geometria euclidiana para espaços que não são necessariamente plana, embora ainda se parecer com o espaço euclidiano em cada ponto "infinitesimal", ou seja, na primeira ordem de aproximação. Vários conceitos com base no comprimento, como o comprimento de arco de curvas , área de regiões planas, e de volume de sólidos todos admitem análogos naturais na geometria de Riemann. A noção de um derivada direcional de uma função do cálculo multivariado é estendido na geometria de Riemann para a noção de um derivada covariante de um tensor. Muitos conceitos e técnicas de análise e de equações diferenciais foram generalizados para a definição de variedades de Riemann.
Um preservar distância difeomorfismo entre variedades de Riemann é chamado de isometria. Esta noção também pode ser definida localmente, ou seja, para as pequenas vizinhanças de pontos. Quaisquer duas curvas regulares são localmente isométrica. No entanto, Theorema Egregium de Gauss já mostrou que para superfícies, a existência de uma isometria local impõe fortes condições de compatibilidade em suas métricas: o Curvaturas gaussianas nos pontos correspondentes deve ser o mesmo. Em dimensões superiores, o Riemann curvatura tensor é um importante invariante pointwise associada a uma variedade de Riemann que mede o quão próximo está a ser plana. Uma classe importante de variedades Riemannianas é formado pela Espaços simétricos de Riemann, cuja curvatura é constante. Eles são o mais próximo ao plano "comum" e do espaço considerado em euclidiana e geometria não-euclidiana.
Geometria pseudo-Riemanniana
Geometria pseudo-Riemanniana generaliza geometria de Riemann para o caso em que o tensor métrico não precisa ser definida positiva. Um caso especial deste é um Colector Lorentzian que é a base matemática de Einstein teoria da relatividade geral de gravidade .
Finsler geometria
Geometria Finsler tem o colector Finsler como o principal objecto de estudo - este é um colector com um diferencial Finsler métrica, isto é, uma Banach norma definida em cada espaço tangente. Uma métrica Finsler é uma estrutura muito mais geral do que uma métrica Riemannianos. Uma estrutura Finsler numa variedade M é uma função F: T M → [0, ∞) de tal modo que:
- F (x, meu) = mF (x, y) para todo x, y em T M,
- F é infinitamente diferenciável em T M - {0},
- O Hessian vertical de F 2 é definida positiva.
Geometria simplética
Geometria Simpléctica é o estudo de variedades simpléticas. Um colector de quase simplética é uma variedade diferenciável equipado com um que varia suavemente não degenerado skew-simétrica forma bilinear em cada espaço tangente, ou seja, um não degenerada 2- forma ω, chamado de forma simplética. A variedade simplética é um colector de quase simplética para o qual a forma ω simpléctica está fechado: d ω = 0.
A difeomorfismo entre duas variedades simpléticas que preserva a forma simplética é chamado de simplectomorfismo. Não degenerado inclinar-simétricas formas bilineares só podem existir no mesmo espaços de vetores dimensionais, assim variedades simpléticas necessariamente tem ainda dimensão. Em dimensão 2, uma variedade simplética é apenas um superfície dotado de um formulário de área e um simplectomorfismo é um difeomorfismo de preservação da área. O espaço de fase de um sistema mecânico é uma variedade simplética e eles fizeram uma aparição implícita já no trabalho de Lagrange em mecânica analítica e, posteriormente, em Jacobi e de Hamilton de formulação da mecânica clássica.
Em contraste com a geometria de Riemann, onde a curvatura fornece uma invariante local das variedades de Riemann, O teorema de Darboux afirma que todas as variedades simpléticas são localmente isomorphic. As únicas invariantes de uma variedade simplética são de natureza global e aspectos topológicos desempenhar um papel proeminente na geometria simplética. O primeiro resultado em topologia simplética é provavelmente o Poincaré-Birkhoff teorema, conjecturou por Henri Poincaré e provado por George Birkhoff em 1912. Ele afirma que, se uma área preservação de um mapa torções annulus cada componente limite em direcções opostas, em seguida, o mapa tem, pelo menos, dois pontos fixos.
Contato geometria
Contacte promoções geometria com certas variedades de dimensão ímpar. É perto de geometria simplética e como este último, ela se originou em questões de mecânica clássica. Uma estrutura de contatos em um (2 n +1) -dimensional variedade M é dada por um campo hiperplano H suave no pacote tangente que é tão longe quanto possível de ser associado com os conjuntos de nível de uma função diferenciável em M (o termo técnico é "completamente nonintegrable distribuição tangente hiperplano"). Perto de cada ponto P, uma distribuição hiperplà é determinada por um desaparecimento em nenhum lugar 1-forma  , Que é único até à multiplicação por uma função em nenhuma parte de fuga:
, Que é único até à multiplicação por uma função em nenhuma parte de fuga:
A 1-forma local em M é uma forma de contato, se a restrição da sua exterior derivado de H é um não-degenerada 2-forma e, portanto, induz uma estrutura simplética em H p em cada ponto. Se a distribuição de H pode ser definida por uma forma global de 1-  em seguida, esta forma é o contato se e somente se a forma top-dimensional
em seguida, esta forma é o contato se e somente se a forma top-dimensional
é um forma de volume em M, ou seja, não desaparece em qualquer lugar. Um análogo de contato do teorema de Darboux detém: todas as estruturas de contacto sobre um colector de odd-dimensional são localmente isomorphic e pode ser levado a uma certa forma normal local por uma escolha apropriada do sistema de coordenadas.
Complexo e Kähler geometria
Geometria diferencial complexo é o estudo das variedades complexas. Um colector quase complexo é um colector de reais 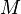 , Dotado com um tensor de Tipo (1,1), isto é, uma endomorphism vetor pacote (chamado de estrutura quase complexa)
, Dotado com um tensor de Tipo (1,1), isto é, uma endomorphism vetor pacote (chamado de estrutura quase complexa)
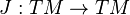 , De tal modo que
, De tal modo que 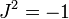 .
.
Decorre desta definição que um colector de quase complexo é ainda dimensional.
Um colector de quase complexo é chamado complexo se 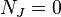 , Onde
, Onde 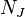 é um tensor do tipo (2,1) relacionado com
é um tensor do tipo (2,1) relacionado com 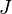 , O chamado Nijenhuis tensor (ou às vezes a torção). Um colector de quase complexo é complexo, se e somente se admite uma holomorphic coordenar atlas. Um estrutura quase Hermitiana é dada por uma estrutura quase complexa J, juntamente com um g métrica riemannian, satisfazendo a condição de compatibilidade
, O chamado Nijenhuis tensor (ou às vezes a torção). Um colector de quase complexo é complexo, se e somente se admite uma holomorphic coordenar atlas. Um estrutura quase Hermitiana é dada por uma estrutura quase complexa J, juntamente com um g métrica riemannian, satisfazendo a condição de compatibilidade 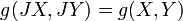 . Uma estrutura quase hermitiana define, naturalmente, um diferencial 2-forma
. Uma estrutura quase hermitiana define, naturalmente, um diferencial 2-forma 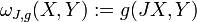 . As duas condições a seguir são equivalentes:
. As duas condições a seguir são equivalentes:
onde  é o Conexão de Levi-Civita
é o Conexão de Levi-Civita 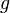 . Neste caso,
. Neste caso,  é chamado um Kähler estrutura, e um colector de Kähler é um colector dotado de uma estrutura Kähler. Em particular, um colector de Kähler é um tanto complexo e um variedade simplética. Uma grande classe de variedades Kähler (a classe de Manifolds Hodge) é dada por toda a suave variedades projetivas complexos.
é chamado um Kähler estrutura, e um colector de Kähler é um colector dotado de uma estrutura Kähler. Em particular, um colector de Kähler é um tanto complexo e um variedade simplética. Uma grande classe de variedades Kähler (a classe de Manifolds Hodge) é dada por toda a suave variedades projetivas complexos.
CR geometria
CR geometria é o estudo da geometria intrínseca de limites de domínios em variedades complexas.
Bundles e conexões
O aparelho de feixes vetor, feixes principais, e conexões neles desempenha um papel extraordinariamente importante na geometria diferencial moderna. Uma variedade suave sempre carrega um pacote vector natural, o pacote tangente. Genericamente falando, esta estrutura por si só é suficiente para o desenvolvimento de análise no colector, ao fazer geometria requer, além de alguma forma relacionar os espaços tangentes em pontos diferentes, ou seja, uma noção de transporte paralelo. Um exemplo importante é fornecido por conexões afim. Para superfície em R3, planos tangentes em diferentes pontos podem ser identificadas utilizando a natureza plana do espaço Euclidiano ambiente. Em Geometria de Riemann, a Conexão de Levi-Civita serve a um propósito similar. De modo mais geral, geômetras diferenciais considerar espaços com um pacote vector e uma conexão como um substituto para a noção de um Variedade de Riemann. Nesta abordagem, o feixe é externo ao colector e tem de ser especificada como uma parte da estrutura, enquanto que a ligação proporciona um aumento adicional. Na física, o distribuidor pode ser o espaço-tempo e feixes e conexões correspondem aos vários campos físicos.
Intrínseca contra extrínseca
Inicialmente e até meados do século XIX , geometria diferencial foi estudado do ponto de vista extrínseca: curvas e as superfícies foram consideradas como encontrando-se em um espaço euclidiano de dimensão mais elevada (por exemplo, uma superfície em uma espaço de três dimensões ambiente). Os resultados mais simples são aqueles em o geometria diferencial de curvas. Começando com o trabalho de Riemann , o ponto de vista intrínseco foi desenvolvido, no qual não se pode falar de mover-se "fora" do objeto geométrico, pois é considerado como dado de forma autônoma.
O ponto de vista intrínseca é mais flexível. Por exemplo, é útil na relatividade onde o espaço-tempo não pode, naturalmente, ser tomado como extrínseco (o que seria "fora" dele?). Com o ponto de vista intrínseco é mais difícil definir o conceito central da curvatura e outras estruturas tais como conexões, para que haja um preço a pagar.
Estes dois pontos de vista podem ser reconciliados, ou seja, a geometria extrínseca pode ser considerada como uma estrutura adicional para a uma intrínseca. (Veja a Nash incorporação teorema.)
Aplicações da geometria diferencial
Abaixo estão alguns exemplos de como a geometria diferencial é aplicada a outros campos da ciência e da matemática.
- Em física , geometria diferencial é o idioma no qual Einstein teoria da relatividade geral é expressa. De acordo com a teoria, o universo é uma variedade suave equipado com métrica pseudo-Riemanniana, que descreveu o curvatura espaço-tempo. Entender essa curvatura é essencial para o posicionamento de satélites em órbita ao redor da Terra. A geometria diferencial também é indispensável no estudo de lentes gravitacionais e buracos negros .
- Em economia , geometria diferencial tem aplicações para o campo da econometria.
- Modelagem geométrica (incluindo computação gráfica) e sorteio design geométrico assistido por computador nas idéias de geometria diferencial.
- Na engenharia , geometria diferencial pode ser aplicada para resolver problemas em processamento de sinal digital.
- Em física , a utilização de formas diferenciais é útil no estudo de electromagnetismo .
- Em física , geometria diferencial tem aplicações tanto para Mecânica de Lagrange e Mecânica hamiltoniana. Colectores simpléticos em particular, podem ser usadas para estudar Sistemas hamiltonianos.