Joseph Louis Lagrange

Joseph Louis, comte de Lagrange
Joseph Louis Lagrange
Nascido	(1736/01/25) 25 de janeiro de 1736 Turin , Sardinia
Morreu	10 de abril de 1813 (1813/04/10) (77 anos) Paris , França
Residência	Sardinia França Prússia
Nacionalidade	Sardo Francês
Campos	Matemática Física matemática
Instituições	École Polytechnique
Conselheiro doutoral	Leonhard Euler
Os estudantes de doutorado	Joseph Fourier Giovanni Plana Simeon Poisson
Conhecido por	Mecânica analítica Mecânica celeste Análise Matemática Teoria dos números
Notas Nota que ele não tinha um conselheiro de doutorado, mas autoridades acadêmicas árvore genealógica vincular sua herança intelectual de Leonhard Euler , que desempenhou o papel equivalente.

Joseph-Louis Lagrange, nascido Giuseppe Lodovico Lagrangia ( 25 de janeiro de 1736 - 10 de abril de 1813 ) foi um Italiano matemático e astrônomo, que viveu a maior parte de sua vida na França , fazendo contribuições relevantes para todos os campos de análise , a teoria dos números , e clássica e mecânica celeste. Na recomendação de Euler e D'Alembert, em 1766 Lagrange sucedeu Euler como diretor de matemática na Academia Prussiana de Ciências, em Berlim , onde permaneceu por mais de vinte anos, produzindo um grande corpo de trabalho e ganhando vários prêmios da Academia Francesa de Ciências. O tratado de Lagrange em mecânica analítica (Mécanique Analítica, 4. ed, 2 vols Paris:.. Gauthier-Villars et Fils, 1888-1889), escrito em Berlim e publicado pela primeira vez em 1788, ofereceu o tratamento mais abrangente da mecânica clássica desde Newton e formou uma base para o desenvolvimento da física matemática no século XIX.

Nascido Giuseppe Lodovico Lagrangia em Turim de pais italianos, Lagrange tinha antepassados franceses no lado de seu pai. Em 1787 ele tornou-se membro da Academia Francesa, e ele permaneceu na França até o fim de sua vida. Portanto, Lagrange é alternativamente considerado um francês e um italiano cientista. Lagrange sobreviveu à Revolução Francesa e se tornou o primeiro professor de análise no École Polytechnique após a sua abertura, em 1794. Napoleão chamado Lagrange para o Legião de Honra e fez dele um Contagem do Império em 1808. Ele está enterrado no Panthéon.

Contribuição científica

Lagrange foi um dos criadores do cálculo das variações , derivando o Euler-Lagrange equações para extrema de funcionais. Ele também estenderam o método para levar em conta possíveis constrangimentos, chegando ao método de Multiplicadores de Lagrange. Lagrange inventou o método de resolução de equações diferenciais conhecidos como variação de parâmetros, aplicado cálculo diferencial para a teoria das probabilidades e alcançou notável trabalho na solução de equações. Ele provou que cada número natural é uma soma de quatro quadrados. Seu tratado Theorie des fonctions analytiques colocou alguns dos fundamentos da teoria do grupo , antecipando Galois. No cálculo , Lagrange desenvolvida uma nova abordagem para interpolação e série de Taylor . Ele estudou o problema dos três corpos para a Terra, Sol e Lua ( 1764 ) eo movimento dos satélites de Júpiter ( 1766 ), e em 1772 encontrou as soluções caso-especial para este problema que hoje são conhecidos como Pontos de Lagrange. Mas acima de tudo ele impressionou na mecânica, tendo transformado a mecânica newtoniana em um ramo da análise, Mecânica lagrangiana como agora é chamado, e exibiu os chamados "princípios" mecânicos como resultado simples do cálculo das variações.

Biografia

Primeiros anos

Lagrange nasceu, de ascendência francesa e italiana (um grande avô paterno era um oficial do exército francês que, em seguida, mudou-se para Turim), como Giuseppe Lodovico Lagrangia em Turim . Seu pai, que tinha cargo da Reino de peito militar da Sardenha, foi de boa posição social e rico, mas antes que seu filho cresceu ele tinha perdido a maior parte de sua propriedade em especulações, eo jovem Lagrange teve que confiar em suas próprias habilidades para a sua posição. Ele foi educado na faculdade de Turim, mas não foi até que ele tinha dezessete anos que ele mostrou qualquer gosto pela matemática - seu interesse no assunto sendo excitado pela primeira vez por um papel por Edmund Halley que ele se deparou por acaso. Sozinho e sem ajuda, ele se jogou em estudos matemáticos; no final de labuta incessante de um ano, ele já era um matemático realizado, e foi feito um professor na escola de artilharia.

Variational cálculo

Lagrange é um dos fundadores do cálculo das variações . Começando em 1754, ele trabalhou no problema da tautochrone, descobrir um método para maximizar e minimizar funcionais de uma forma semelhante ao encontrar os extremos de funções. Lagrange escreveu várias cartas a Leonhard Euler entre 1754 e 1756 descrevendo seus resultados. Ele esboçou seu "δ-algorithm", levando à Euler-Lagrange equações de cálculo das variações e simplificar consideravelmente análise anterior de Euler. Lagrange também aplicou suas ideias para os problemas da mecânica clássica, generalizando os resultados de Euler e Maupertuis.

Euler foi muito impressionado com os resultados de Lagrange. Tem sido, por vezes, afirmou que "com cortesia característica que ele reteve um papel que tinha escrito anteriormente, que cobriu alguns dos o mesmo terreno, a fim de que o jovem italiano pode ter tempo para concluir seu trabalho, e reivindicar a invenção indiscutível do novo cálculo "No entanto, este ponto de vista de cavalaria tem vindo a ser contestada. Lagrange publicou seu método em duas memórias da Sociedade Turim em 1762 e 1773.

Miscelânea Taurinensia

Em 1758 , com a ajuda de seus alunos, Lagrange estabeleceu uma sociedade, que foi posteriormente incorporada como a Turin Academy of Sciences, ea maioria de seus primeiros escritos encontram-se nos cinco volumes de suas operações, geralmente conhecida como a Miscellanea Taurinensia. Muitos deles são papéis elaborados. O primeiro volume contém um artigo sobre a teoria da propagação do som; neste ele indica um erro cometido por Newton , obtém o general equação diferencial para o movimento, e integra-lo para o movimento em uma linha reta. Este volume também contém a solução completa do problema de uma cadeia de vibração transversalmente; neste trabalho ressalta a falta de generalidade nas soluções previamente dadas por Brook Taylor, D'Alembert, e Euler, e chega à conclusão de que a forma da curva em qualquer instante t, é dado pela equação 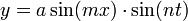. O artigo conclui com uma discussão magistral de ecos, batidas e sons compostos. Outros artigos neste volume estão em recorrente série, probabilidades , eo cálculo das variações .

O segundo volume contém um longo papel que contém os resultados de vários papéis no primeiro volume sobre a teoria ea notação do cálculo das variações; e ele ilustra seu uso através da dedução da princípio de ação mínima, e por soluções de vários problemas em dinâmica.

O terceiro volume inclui a solução de vários problemas dinâmicos por meio do cálculo das variações; alguns artigos sobre o cálculo integral ; uma solução de Fermat problema 's mencionado acima, para encontrar um número x que fará com que (x ² n + 1) a praça onde n é um inteiro dado que não é um quadrado; e as equações diferenciais gerais Proposta de três corpos em movimento sob suas atrações mútuas.

O próximo trabalho que ele produziu foi em 1764 no libração da Lua , e uma explicação de por que o mesmo rosto estava sempre se voltou para a terra, um problema que ele tratou com a ajuda de trabalho virtual. Sua solução é especialmente interessante como contendo o germe da idéia de equações generalizadas de movimento, equações que ele formalmente pela primeira vez provadas em 1780 .

Berlin Academy

Já em 1756 Euler, com o apoio da Maupertuis, fez uma tentativa para trazer Lagrange para a Academia de Berlim. Mais tarde, D'Alambert interferiu em nome de Lagrange com Frederico da Prússia e escreveu para Lagrange pedindo-lhe para deixar de Turim para uma posição consideravelmente mais prestigiada em Berlim. Lagrange recusou ambas as ofertas, respondendo em 1765 que

Parece-me que Berlim não seria de todo adequado para mim enquanto M.Euler está lá.

Em 1766 Euler deixou Berlim para São Petersburgo , e Frederick escreveu para Lagrange manifestando o desejo de "o maior rei na Europa" para ter "o maior matemático na Europa" residente em sua corte. Lagrange foi finalmente convenceu e ele passou os próximos 20 anos em Prússia, onde produziu não só a longa série de artigos publicados nas transações Berlim e Turim, mas sua obra monumental, o analytique Mécanique. Sua residência em Berlim, começou com um erro lamentável. Encontrar maioria de seus colegas casados, e assegurada por suas esposas que era a única maneira de ser feliz, ele se casou; sua esposa logo morreu, mas a união não foi feliz.

Lagrange era um dos favoritos do rei, que usou com freqüência para discursar com ele sobre as vantagens da perfeita regularidade da vida. A lição foi para casa, e daí em diante Lagrange estudou seu corpo e mente como se fossem máquinas, e encontrado por experimento a quantidade exata de trabalho que ele era capaz de fazer sem quebrar. Toda noite ele pôs-se uma tarefa definida para o dia seguinte, e em completar qualquer ramo de um assunto que ele escreveu uma breve análise para ver o que aponta nas manifestações ou no objecto eram capazes de melhoria. Ele sempre pensou que o assunto de seus papéis antes que ele começou a compor-los, e, geralmente, escreveu-los em linha reta fora sem um único apagamento ou correção.

França

Em 1786 , Frederick morreu, e Lagrange, que havia encontrado o clima de Berlim tentando, aceitou de bom grado a oferta de Louis XVI a migrar para Paris. Ele recebeu convites semelhantes de Espanha e Naples. Na França, ele foi recebido com cada marca de distinção e especiais apartamentos no Louvre foram preparados para sua recepção, e ele se tornou um membro da Academia Francesa de Ciências, que mais tarde tornou-se parte da Instituto Nacional. No início de sua residência em Paris, ele foi apreendido com um ataque da melancolia, e até mesmo a cópia impressa de seu Mécanique no qual ele havia trabalhado durante um quarto de século para lançar mais de dois anos fechados em sua mesa. Curiosidade como para os resultados da revolução francesa moveu primeiro a sair da sua letargia, uma curiosidade que logo se transformou em alarme como a revolução desenvolvido.

Era quase ao mesmo tempo, 1792 , que a tristeza inexplicável de sua vida e sua timidez movido a compaixão de uma jovem que insistia em se casar com ele, e provou ser uma esposa dedicada a quem ele se calorosamente anexado. Embora o decreto de Outubro de 1793 que ordenou que todos os estrangeiros a deixar a França isenta-lo especificamente pelo nome, ele se preparava para fugir quando foi oferecido a presidência da comissão para a reforma dos pesos e medidas. A escolha das unidades finalmente selecionados foi em grande parte devido a ele, e foi principalmente devido à sua influência que a subdivisão decimal foi aceito pela comissão de 1799 . Em 1795, Lagrange foi um dos membros fundadores da Bureau des Longitudes.

Embora Lagrange tinha determinado a escapar da França enquanto ainda havia tempo, ele nunca esteve em perigo; e os diferentes governos revolucionários (e mais tarde, Napoleão ) carregado ele com honras e distinções. Um testemunho impressionante ao respeito que ele realizou foi mostrado em 1796 , quando o comissário francês em Itália foi condenada a participar no estado de completo sobre o pai de Lagrange, e ofertar as felicitações da república sobre as realizações de seu filho, que "tinha feito honrar a toda a humanidade por seu gênio, e quem era a glória especial de Piedmont ter produzido ". Pode acrescentar-se que Napoleão, quando ele alcançou o poder, calorosamente encorajados estudos científicos na França, e foi um benfeitor liberal deles.

École Normale

Em 1795 , Lagrange foi nomeado para uma cadeira de matemática na recém-criada École Normale, que contou com apenas uma breve existência de quatro meses. Suas palestras aqui foram bastante elementar, e não contêm nada de qualquer importância especial, mas eles foram publicados porque os professores tinham que "comprometem-se aos representantes do povo e uns aos outros nem ler nem repetir de memória," e os discursos foram ordenados a ser tomadas para baixo em taquigrafia, a fim de permitir que os deputados para ver como os professores absolvido si.

École Polytechnique

Lagrange foi nomeado professor da École Polytechnique, em 1794; e suas palestras são descritos pelos matemáticos que tiveram a sorte de ser capaz de assistir a elas, como quase perfeita, tanto em forma e matéria. Começando com os elementos merest, ele levou seus ouvintes sobre até que, quase desconhecido para si mesmos, eles mesmos eram ampliação dos limites do objecto: acima de tudo, ele impressionou em seus alunos a vantagem de sempre usando métodos gerais expressos em uma notação simétrico.

Por outro lado, Fourier, que participou suas palestras em 1795, escreveu:

Sua voz é muito fraco, pelo menos na medida em que ele não se torna aquecida; ele tem um sotaque italiano muito pronunciado e pronuncia as s como z ... Os alunos, dos quais a maioria são incapazes de apreciar-lo, dar-lhe pouco bem-vindo, mas os professores fazer as pazes por isso.

Anos de atraso

O túmulo de Lagrange na cripta da Panthéon.

Em 1810 , Lagrange iniciou uma revisão aprofundada da analytique Mécanique, mas ele foi capaz de completar apenas cerca de dois terços do que antes de sua morte em 1813. Ele foi enterrado no mesmo ano no Panthéon em Paris. A inscrição francês em seu túmulo há lê:

JOSEPH LOUIS LAGRANGE. O senador. Contagem do Império. Grande Oficial da Legião de Honra. Grã-Cruz da Ordem Imperial da Reunião. Membro do Instituto ea Secretaria de Longitude. Nascido em Turim em 25 de janeiro 1736. Morreu em Paris em 10 de abril de 1813.

Trabalho em Berlim

Lagrange foi cientificamente extremamente ativo durante 20 anos que passou em Berlim. Não só ele produzir sua esplêndida analytique Mécanique, mas ele contribuiu com entre um e duzentos trabalhos para a Academia de Turim, a Academia de Berlim, e da Academia Francesa. Alguns deles são realmente tratados, e todos, sem exceção são de alta ordem de excelência. Exceto por um curto período de tempo quando ele estava doente, ele produziu, em média, cerca de um papel por mês. Destes, observe o seguinte, como entre os mais importantes.

Primeiro, suas contribuições para o quarto e quinto volumes, 1766 - 1,773 , do Miscellanea Taurinensia; dos quais o mais importante foi o de 1771 , em que ele discutiu como numerosos astronômicos observações devem ser combinadas de modo a dar o resultado mais provável. E mais tarde, suas contribuições para os dois primeiros volumes, 1784 - 1785 , das operações da Academia de Turim; a primeira das quais ele contribuiu com um papel sobre a pressão exercida por um fluido em movimento, e a segunda um artigo sobre a integração por série infinita, e o tipo de problemas para os quais ele é adequado.

A maioria dos trabalhos enviados para Paris estavam em questões astronômicas, e entre estes deve-se mencionar em particular o seu papel na Sistema Jovian em 1766, seu ensaio sobre o problema dos três corpos em 1772 , o seu trabalho sobre a equação secular da Lua em 1773 , e seu tratado sobre perturbações de cometas em 1778. Estes foram todos escritos sobre temas propostos pela Académie française e, em cada caso, o prémio foi atribuído a ele.

Mecânica lagrangiana

Entre 1772 e 1788, Lagrange re-formulado mecânica clássica newtoniana / fórmulas para simplificar e facilitar os cálculos. Estes mecanismos são chamados Mecânica de Lagrange.

Álgebra

O maior número de seus papéis durante este tempo foram, no entanto, contribuiu para a Academia Prussiana de Ciências. Vários deles lidar com questões de álgebra .

• Sua discussão de representações de inteiros por formas quadráticas (1769) e por formas algébricas mais gerais (1770).
• Seu tratado sobre a Teoria da Eliminação de 1770.
• O teorema de Lagrange que o fim de um subgrupo H de um grupo G tem de dividir o fim de G.
• Seus trabalhos de 1770 e 1771 sobre o processo geral para a resolução de um equação algébrica de qualquer grau através dos resolventes de Lagrange. Este método não consegue dar uma fórmula geral para soluções de uma equação de grau cinco e mais alto, porque a equação auxiliar os envolvidos têm maior grau do que o original. A importância deste método é que ele exibe as fórmulas já conhecidos para a resolução de equações de segundo, terceiro, e quarto graus, como maniferstations de um único princípio. A solução completa de uma equação binomial de qualquer grau, também é tratada nestes documentos.
• Em 1773, considerado um Lagrange determinante funcional de ordem 3, um caso especial de um Jacobian. Ele também mostrou a expressão para o volume de um tetraedro com um dos vértices na origem como a um sexto do valor absoluto do determinante formado pelas coordenadas dos outros três vértices.

Teoria dos Números

Vários de seus primeiros papéis também lidam com questões de teoria dos números.

• Lagrange (1766-1769) foi a primeira a demonstrar que A equação de Pell 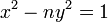tem uma solução não trivial em números inteiros para qualquer número natural não-quadrado n.
• Ele provou o teorema, afirma Bachet sem justificação, que cada inteiro positivo é a soma de quatro quadrados, 1770.
• Ele provou Teorema de Wilson que, se n é um primo, então (n - 1)! + 1 é sempre um múltiplo de N, 1,771.
• Seus papéis de 1773, 1775, 1777 e deu demonstrações de vários resultados enunciados por Fermat, e não previamente provada.
• Deu um método para a determinação dos elementos de números da forma

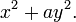
Outro trabalho matemático

Há também inúmeros artigos sobre diversos pontos de geometria analítica . Em dois deles, escrito em vez mais tarde, em 1792 e 1793 , ele reduziu o equações das quádricas (ou conicoids) aos seus respectivos formas canônicas.

Durante os anos de 1772 a 1785 , ele contribuiu com uma longa série de documentos que criou a ciência de equações diferenciais parciais . Uma grande parte desses resultados foram coletados na segunda edição do cálculo integral de Euler, que foi publicado em 1794 .

Ele fez contribuições à teoria de frações contínuas.

Astronomia

Por último, existem inúmeros artigos sobre problemas em astronomia . Destes os mais importantes são os seguintes:

• A tentativa de resolver o problema dos três corpos resultando na descoberta de Pontos de Lagrange, 1772
• Na atração de elipsóides, 1773: este é fundada sobre O trabalho de Maclaurin.
• Na equação secular da Lua, 1773; também perceptível para a primeira introdução da idéia do potencial. O potencial de um corpo em qualquer ponto é a soma da massa de cada elemento do corpo quando dividido pela sua distância a partir do ponto. Lagrange mostrou que, se o potencial de um organismo a um ponto externo eram conhecidos, a atracção em qualquer direcção ao mesmo tempo pode ser encontrado. A teoria do potencial foi elaborado em um documento enviado a Berlim em 1777.
• No movimento dos nós de um planeta de orbitar de 1774.
• Sobre a estabilidade das órbitas planetárias, 1776.
• Dois artigos em que o método de determinação da órbita de um cometa a partir de três observações é completamente trabalhados, 1778 e 1783: isto não tem realmente provou praticamente possível, mas o seu sistema de cálculo das perturbações por meio de quadraturas mecânicos formou a base de a maioria das pesquisas posteriores sobre o assunto.
• Sua determinação das variações seculares e periódicas da elementos dos planetas, 1781-1784: os limites máximos atribuídos para estes concordam em estreita colaboração com os obtidos mais tarde por Le Verrier, e procedeu Lagrange, tanto quanto o conhecimento então possuía das massas dos planetas permitidas.
• Três artigos sobre o método de interpolação, 1783, 1792 e 1793: a parte de diferenças finitas que lidam com ela está agora no mesmo palco como aquele em que Lagrange deixou.

Mécanique analytique

Para além destes vários papéis que ele compôs seu grande tratado, o analytique Mécanique. Nisso, ele estabelece a lei do trabalho virtual, e de que um princípio fundamental, com a ajuda do cálculo das variações, deduz a totalidade da mecânica, tanto de sólidos e líquidos.

O objectivo do livro é mostrar que o objecto está implicitamente incluídos num único princípio, e para dar fórmulas gerais a partir da qual qualquer consequência particular pode ser obtidos. O método de coordenadas generalizadas pelo qual alcançou esse resultado é talvez o resultado mais brilhante de sua análise. Em vez de seguir o movimento de cada parte individual de um sistema de materiais, como D'Alembert e Euler tinha feito, mostrou que, se determinar a sua configuração por um número suficiente de variáveis cujo número é a mesma que a dos graus de liberdade possuída pelo sistema, em seguida, as energias cinéticas e potenciais do sistema pode ser expressa em termos de tais variáveis, e as equações diferenciais de movimento daí deduzida por diferenciação simples. Por exemplo, na dinâmica de um sistema rígido que substitui a consideração do problema particular pela equação geral, que é agora normalmente escrito na forma

T para a energia cinética e V para a energia potencial. Entre outros teoremas menores aqui dado pode mencionar a proposição de que a energia cinética transmitida pelos impulsos dado a um sistema material sob determinadas restrições é um máximo, ea princípio de ação mínima. Toda a análise é tão elegante que Sir William Rowan Hamilton disse que o trabalho só poderia ser descrito como um poema científico. Pode ser interessante notar que Lagrange observou que a mecânica foi realmente um ramo da matemática pura análogas a uma geometria de quatro dimensões, ou seja, o tempo e as três coordenadas do ponto no espaço; e diz-se que ele se orgulhava de que desde o início até o fim do trabalho não havia um único diagrama. À primeira qualquer impressora pode ser encontrado que iria publicar o livro; mas Legendre finalmente convenceu uma empresa de Paris para realizar-lo, e ele foi emitido sob sua supervisão em 1788.

Uma importante contribuição para a mecânica dos fluidos foi o conceito de "fluxo potencial", muitas vezes associada, de forma errada, com a noção de fluido ideal, invíscido. O desenvolvimento inicial de Joseph-Louis Lagrange (1781) introduziu o potencial de velocidade para o fluido flua reais, desde que a resultante das forças deriva de um potencial. No mesmo artigo, Lagrange também apresentou o conceito de função de corrente e a equação da celeridade de uma pequena perturbação em águas rasas. A contribuição de Lagrange em 1781 foi notável e foi verdadeiramente à frente de seu tempo.

Trabalho na França

Cálculo diferencial e cálculo das variações

Palestras de Lagrange sobre o cálculo diferencial na École Polytechnique formam a base de seu tratado Théorie des fonctions analytiques, que foi publicado em 1797. Este trabalho é a extensão de uma idéia contida em um papel que ele tinha enviado para os jornais de Berlin em 1772, e seu objeto é substituir para o cálculo diferencial um grupo de teoremas com base no desenvolvimento de funções algébricas em série. Um método um tanto semelhante tinha sido previamente utilizado por John Landen na Análise de Resíduos, publicado em Londres em 1758. Lagrange acreditava que ele poderia, assim, se livrar dessas dificuldades, conectados com o uso de quantidades infinitamente grandes e infinitamente pequenas, para que os filósofos se opuseram no tratamento usual do cálculo diferencial. O livro é dividido em três partes: destes, os primeiros trata da teoria geral das funções, e dá uma prova algébrica de teorema de Taylor , cuja validade é, no entanto, aberto a questão; a segunda trata de aplicações à geometria; eo terceiro com aplicações à mecânica. Outro tratado nas mesmas linhas foram seus Leçons sur le calcul des fonctions, emitido em 1804 , com a segunda edição em 1806. É neste livro que Lagrange formulou sua célebre método de Multiplicadores de Lagrange, no contexto de problemas de cálculo das variações com restrições integrais. Estas obras dedicadas ao cálculo diferencial e cálculo das variações pode ser considerado como o ponto de partida para as pesquisas de Cauchy, Jacobi, e Weierstrass.

Infinitesimais

Em um período posterior Lagrange revertido para o uso de infinitesimais de preferência a fundar o cálculo diferencial no estudo de formas algébricas; e no prefácio à segunda edição da Mecânica, que foi emitida em 1811 , ele justifica o emprego de infinitesimais, e conclui dizendo que:

Quando compreenderam o espírito do método infinitesimal, e verificaram a exatidão de seus resultados, quer pelo método geométrico dos rácios de primeira linha e finais, ou pelo método de análise de funções derivadas, podemos empregar quantidades infinitamente pequenas como uma certeza e valioso meio de encurtar e simplificar as nossas provas.

Frações contínuas

Sua Résolution des équations numériques, publicado em 1798 , também foi o fruto das suas palestras na École Politécnica. Lá, ele dá o método de aproximação para as verdadeiras raízes de uma equação por meio de fracções continuou, e enuncia vários outros teoremas. Em uma nota no final ele mostra como Pequeno teorema de Fermat que

um ^{p -1} - 1 ≡ 0 (mod p)

em que p é um número primo e um é primo para p, pode ser aplicado para se obter a solução completa algébrica de qualquer equação binomial. Ele também aqui explica como a equação cujas raízes são os quadrados das diferenças das raízes da equação original pode ser usada de modo a dar informação considerável quanto à posição e natureza dessas raízes.

A teoria da movimentos planetários tinham sido objecto de alguns dos mais notáveis dos papéis de Berlim de Lagrange. Em 1806 o tema foi reaberto por Poisson, que, em um papel lido antes da Academia Francesa, mostrou que as fórmulas de Lagrange levou a determinados limites para a estabilidade das órbitas. Lagrange, que estava presente, agora discutido o assunto inteiro de novo, e numa carta comunicada à Academy em 1808 explicou como, pela variação de constantes arbitrárias, o periódico e as desigualdades seculares de qualquer sistema de organismos que interagem mutuamente pôde ser determinado.

Prémios e distinções

Euler propôs Lagrange para a eleição para a Academia de Berlim e foi eleito em 2 de setembro de 1756. Ele foi eleito Fellow da Royal Society de Edimburgo, em 1790, e um membro da Royal Society em 1791. Em 1808 , Napoleão fez Lagrange um Grande Oficial da Legião de Honra e um Comte do Império. Ele foi premiado com o Grande Croix do Ordre Impérial de la Réunion em 1813 , uma semana antes de sua morte, em Paris.

Lagrange foi agraciado com o prêmio 1764 da Academia Francesa de Ciências para o seu livro de memórias sobre a libração da Lua. Em 1766 a Academia propôs um problema do movimento do satélites de Júpiter, e novamente o prêmio foi concedido a Lagrange. Ele também ganhou os prêmios de 1772, 1774 e 1778.

Lagrange é um dos 72 proeminentes cientistas franceses que foram celebrado em placas na primeira fase do Torre Eiffel quando foi inaugurada. Rue Lagrange no 5º Arrondissement em Paris é nomeado após ele. Em Turim, a rua onde a casa de seu nascimento ainda está de pé é nomeado através de Lagrange. Cratera lunar Lagrange também leva seu nome.

Apocrypha

• Ele era de estatura média e um pouco formada, com olhos azuis e uma pele incolor. Ele estava nervoso e tímido, ele detestava polêmica, e, para evitá-lo, voluntariamente permitiu que outros levar o crédito por aquilo que ele mesmo tinha feito.

• Diz-se que ele foi capaz de escrever seus papéis completa sem uma única correcção necessária.