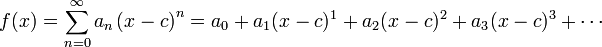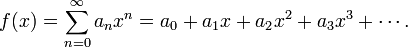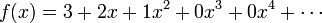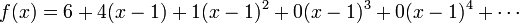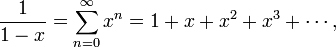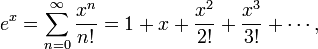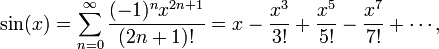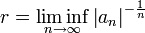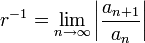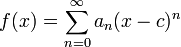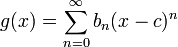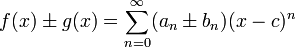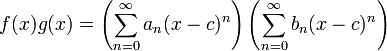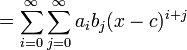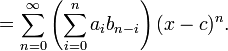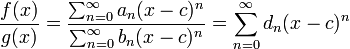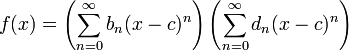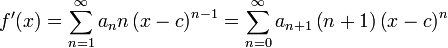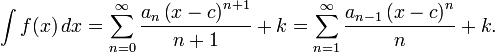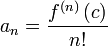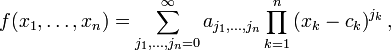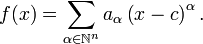Séries de potências

Assuntos Relacionados: Matemática

Fundo para as escolas Wikipédia

Esta seleção Wikipedia está offline disponível a partir de Crianças SOS, para distribuição no mundo em desenvolvimento. Uma boa maneira de ajudar outras crianças é por patrocinar uma criança

Em matemática , uma série de potência (em uma variável) é um infinita série do formulário

$f (x) = \ sum_ {n = 0} ^ \ infty a_n \ left (xc \ right) ^ n = a_0 + a_1 (xc) ^ 1 + a_2 (xc) ^ 2 + a_3 (xc) ^ 3 + \ cdots$

em que _n representa um coeficiente de o n-ésimo termo, c é uma constante e x varia em torno de c (por esta razão, por vezes, uma fala da série como estando centrada em c). Esta série geralmente surge como a série de Taylor de algumas conhecidas função ; a série de Taylor artigo contém muitos exemplos.

Em muitas situações, c é igual a zero, por exemplo, quando se considera uma série de Maclaurin . Em tais casos, a série de potência assume a forma mais simples

$f (x) = \ sum_ {n = 0} ^ \ infty a_n x ^ n = A_0 + A_1 x + a_2 x ^ 2 + a_3 x ^ 3 + \ cdots.$

Estas séries de poder surgir principalmente na análise, mas também ocorrem em combinatória (sob o nome de gerando funções) e em engenharia elétrica (sob o nome do Z-transform). O familiar notação decimal para números inteiros também pode ser vista como um exemplo de uma série de potência, mas com o argumento x fixado em 10. Em teoria número , o conceito de números p-adic está também intimamente relacionada com a de uma série de fontes.

A função exponencial (em azul), ea soma dos primeiros n 1 termos de sua série de potência Maclaurin (em vermelho).

Exemplos

Qualquer polinomial pode ser facilmente expresso como uma série de potência em torno de qualquer centro C, ainda que com a maioria dos coeficientes iguais a zero. Por exemplo, o polinómio 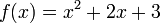$f (x) = x ^ 2x + 2 + 3$ pode ser escrito como uma série de potências em torno do centro 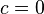$c = 0$ como

$f (x) = 3 + 2 + 1 x x ^ 0 x 2 + 3 + 0 ^ x ^ 4 + \ cdots \,$

ou em torno do centro 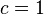$c = 1$ como

$f (x) = 6 + 4 (x-1) + 1 (x-1) ^ 2 + 0 (x-1) ^ 3 + 0 (x-1) + ^ 4 \ cdots \,$

ou mesmo em torno de qualquer outro centro C. Pode-se ver séries de potências como sendo "polinômios de grau infinito", apesar de série de potência não são polinômios.

O fórmula série geométrica

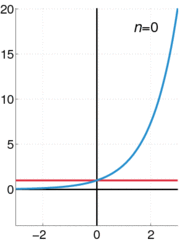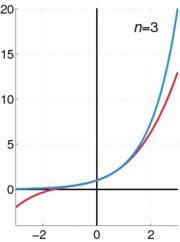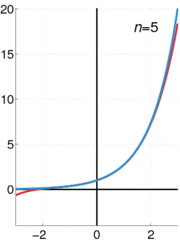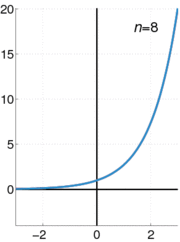
$\ frac {1} {1}-x = \ sum_ {n = 0} ^ \ infty x ^ n = 1 + x + x ^ 2 + x ^ 3 + \ cdots,$

que é válido para 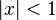$| X | <1$ , É um dos exemplos mais importantes de uma série de fontes, assim como a fórmula função exponencial

$e ^ x = \ sum_ {n = 0} ^ \ infty \ frac {x ^ n} {n!} = 1 + x + \ frac {x ^ 2} {2!} + \ frac {x ^ 3} { 3!} + \ cdots,$

e a fórmula seno

$\ Sin (x) = \ sum_ {n = 0} ^ \ infty \ frac {(- 1) ^ nx ^ {2n + 1}} {(2n + 1)! = X} - \ frac {x ^ 3} {3!} + \ frac {x ^ 5} {5!} - \ frac {x ^ 7} {!} + \ 7 cdots,$

válido para todos reais x. Estas séries de energia também são exemplos de séries de Taylor .

Poderes negativos não são permitidos em uma série de potência, por exemplo 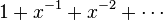$1 + x ^ {- 1} + x ^ {- 2} + \ cdots$ não é considerada uma série de potência (embora seja Série Laurent). Poderes Do mesmo modo, tais como fraccionais 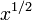$x ^ {1/2}$ não são permitidas (mas veja Série Puiseux). Os coeficientes 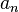$a_n$ não estão autorizados a depender 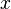$x$ , Assim, por exemplo:

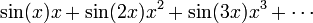$\ Sin (x) x + \ sin (2x) x ^ 2 + \ sin (3x) x ^ 3 + \ cdots \,$ não é uma série de potência.

Raio de convergência

Uma série de potência irá convergir para alguns valores da variável x e podem divergir para outros. Todas as séries de energia irão convergir em x = c. Há sempre um número r com 0 ≤ r ≤ ∞ tal que a série converge quando | x - c | <r e diverge quando | x - c |> r. O número r é o chamado raio de convergência da série de poder; Em geral, é dada como

$r = \ liminf_ {n \ to \ infty} \ left | a_n \ right | ^ {- \ frac {1} {n}}$

ou, de forma equivalente,

$r ^ {- 1} = \ limsup_ {n \ to \ infty} \ left | a_n \ right | ^ {\ frac {1} {n}}$

(Veja limitar superior e limite inferior). Uma maneira rápida de calcular é

$r ^ {- 1} = \ lim_ {n \ to \ infty} \ left | {a_ {n + 1} \ over a_n} \ right |$

Se este limite existe.

As séries converge absolutamente para | x - c | <r e converge uniformemente em toda compacta subconjunto de {x: | x - c | <r}.

Para | x - c | = r, não podemos fazer qualquer declaração geral sobre se a série converge ou diverge. No entanto, O teorema de Abel afirma que a soma da série é contínua em x, se a série converge em x.

Operações em série de potência

Adição e subtração

Quando duas funções f e g são decompostos em série de potência em torno do mesmo centro C, a série de potências da soma ou diferença das funções pode ser obtido através da adição e subtracção termwise. Isto é, se:

$f (x) = \ sum_ {n = 0} ^ \ infty a_n (x-c) ^ n$

$g (x) = \ sum_ {n = 0} ^ \ infty b_n (x-c) ^ n$

em seguida

$f (x) \ pm g (x) = \ sum_ {n = 0} ^ \ infty (a_n \ pm b_n) (xc) ^ n$

Multiplicação e divisão

Com as mesmas definições acima referidas, para a série de potência do produto e quociente das funções pode ser obtido como se segue:

$f (x) g (x) = \ left (\ sum_ {n = 0} ^ \ infty a_n (xc) ^ n \ right) \ left (\ sum_ {n = 0} ^ \ infty b_n (xc) ^ n \ right)$

$= \ Sum_ {i = 0} ^ \ infty \ sum_ {j = 0} ^ \ infty a_i b_j (xc) ^ {i + j}$

$= \ Sum_ {n = 0} ^ \ infty \ left (\ sum_ {i = 0} ^ n a_i b_ {ni} \ right) (xc) ^ n.$

A sequência 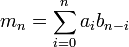$m_n = \ sum_ {i = 0} ^ n a_i b_ {n-i}$ é conhecido como o convolução das sequências 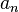$a_n$ e $b_n$ .

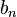Para a divisão, observe:

${F (x) \ over g (x)} = {\ sum_ {n = 0} ^ \ infty a_n (xc) ^ n \ over \ sum_ {n = 0} ^ \ infty b_n (xc) ^ n} = \ sum_ {n = 0} ^ \ infty d_n (xc) ^ n$

$f (x) = \ left (\ sum_ {n = 0} ^ \ infty b_n (xc) ^ n \ right) \ left (\ sum_ {n = 0} ^ \ infty d_n (xc) ^ n \ right)$

e depois use o acima, comparando coeficientes.

Diferenciação e integração

Uma vez que a função é dada como uma série de potência, que é contínua onde quer que converge e é diferenciável no interior desse conjunto. Pode ser diferenciada e integrada com bastante facilidade, tratando cada termo separadamente:

$f ^ \ prime (x) = \ sum_ {n = 1} ^ \ infty a_n n \ left (xc \ right) ^ {n-1} = \ sum_ {n = 0} ^ \ infty a_ {n + 1} \ left (n + 1 \ right) \ left (xc \ right) ^ {n}$

$\ Int f (x) \, dx = \ sum_ {n = 0} ^ \ infty \ frac {a_n \ left (xc \ right) ^ {n + 1}} {n + 1} + k = \ sum_ {n = 1} ^ \ infty \ frac {a_ {n-1} \ left (xc \ right) ^ {n}} {n} + k.$

Ambas as séries de ter o mesmo raio de convergência que o original.

Funções analíticas

Uma função f definida em alguns subconjunto aberto U de R ou C é chamado analítico se for dada localmente por série de potência. Isto significa que cada um ∈ L tem um aberto bairro V ⊆ U, de tal forma que existe uma série de potência com um centro que converge para f (x) para todo x ∈ V.

Cada série de potência com um raio positivo de convergência é analítica sobre a interior de sua região de convergência. Tudo funções holomorfas são complexas-analítica. Somas e produtos de funções analíticas são analíticas, como são quocientes enquanto o denominador é diferente de zero.

Se uma função analítica é, em seguida, é infinitamente muitas vezes diferenciável, mas no caso real o inverso não é geralmente verdadeiro. Para uma função analítica, os coeficientes de um _n pode ser calculado como

$a_n = \ frac {f ^ {\ left (n \ right)} \ left (c \ right)} {n!}$

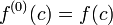onde $f ^ {(n)} (c)$ indica o enésimo derivado de f em C, e $f ^ {(0)} (c) = f (c)$ . Isto significa que cada função analítica é representada localmente por sua série de Taylor .

A forma global de uma função analítica é completamente determinada pelo seu comportamento local no seguinte sentido: se f e g são duas funções analíticas definidos na mesma Conjunto aberta ligada L, e se existe uma (c) = g ⁽ⁿ⁾ (c) c elemento ∈ U tal que f ⁽ⁿ⁾ para todos os n ≥ 0, então f (x) = g (x) para todos os x ∈ U.

Se uma série de potência com raio de convergência r é dado, pode-se considerar continuações analíticas da série, ou seja, funções analíticas f que são definidos em conjuntos maiores que {x: | x - c | <r} e concorda com a série de poder dado sobre este conjunto. O número r é máxima no sentido seguinte: existe sempre um número complexo com x | x - a | = r tal que nenhum continuação analítica da série pode ser definido em x.

A expansão em série de potências da função inversa de uma função analítica pode ser determinada utilizando o Lagrange teorema de inversão.

Séries de potências formais

Em álgebra abstrata , um tenta capturar a essência da série de potência, sem ficar restrito ao campos de números reais e complexos, e sem a necessidade de falar sobre convergência. Isto leva ao conceito de série de potências formal, um conceito de grande utilidade na combinatória algébrica.

Série de potência em várias variáveis

Uma extensão da teoria é necessário para fins de cálculo multivariada. Uma série de potência é aqui definido como sendo uma série infinita da forma

$f (x_1, \ dots, x_n) = \ sum_ {j_1, \ dots, j_n = 0} ^ {\ infty} {a_ j_1, \ pontos, j_n} \ Prod_ {k = 1} ^ n \ left (x_k - c_k \ right) ^ {} j_k,$

em que j = (j _1, ..., j _n) é um vector de números naturais, os coeficientes A _{(J 1, ..., j n)} são geralmente números reais ou complexos, e o centro c = (c ₁ , ..., c _n) e argumento x = (x _1, ..., x _n) são geralmente vectores reais ou complexos. No mais conveniente multi-índice de notação isso pode ser escrito

$f (x) = \ sum _ {\ alpha \ in \ mathbb {N} ^ n} uma _ {\ alpha} \ left (x - c \ right) ^ {\ alpha}.$

A teoria de tal série é mais complicado do que para a série única variável, com regiões mais complicadas de convergência. Por exemplo, a série de potência 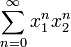$\ Sum_ {n = 0} ^ \ infty x_1 x_2 ^ n ^ n$ é absolutamente convergente no set 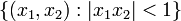$\ {(X_1, x_2): | x_1 x_2 | <1 \}$ entre duas hipérboles. (Este é um exemplo de um conjunto de log-convexo, no sentido de que o conjunto de pontos 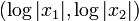$(\ Log | x_1 | \ log | x_2 |)$ , Onde 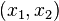$(X_1, x_2)$ encontra-se na região acima, é um conjunto convexo. Mais geralmente, pode-se mostrar que, quando C = 0, o interior da região de convergência absoluta é sempre um conjunto de log-convexa neste sentido.) Por outro lado, no interior da região de convergência pode-se diferenciar e integrar sob o signo série, assim como uma série de maio, com poder ordinário.

Ordem de uma série de potência

Deixe α ser um multi-índice para uma série de potências f (x _1, x _2, ..., x _n). A ordem da série de fontes de f é definida como sendo o valor mínimo | α | de tal modo que um _α ≠ 0, ou 0 se f ≡ 0. Em particular, para uma série de fontes de f (x) numa única variável x, a ordem de f é a menor potência de x com um coeficiente diferente de zero. Esta definição é prontamente estendida a Série Laurent.

Retirado de " http://en.wikipedia.org/w/index.php?title=Power_series&oldid=201226722 "

We provide Linux to the World