Riemann superfície

Riemann superfície para a função f (z) = sqrt (z)

Em matemática , em particular no análise complexa, uma superfície de Riemann, primeiramente estudados por e nomeado após Bernhard Riemann , é um one-dimensional variedade complexa. Superfícies de Riemann pode ser pensado como "versões deformadas" do plano complexo : localmente perto de cada ponto de eles se parecem com pedaços de plano complexo, mas global topologia pode ser bem diferente. Por exemplo, eles podem olhar como uma esfera ou um toro ou um par de folhas coladas.

O principal ponto de superfícies de Riemann é que holomorfos funções podem ser definidas entre elas. Superfícies de Riemann são hoje considerados o cenário natural para o estudo do comportamento global destas funções, especialmente funções com valores múltiplos, como a raiz quadrada e outra funções algébricas, ou o logaritmo .

Cada superfície de Riemann é uma analítica verdadeira bidimensional colector (ou seja, uma superfície), mas contém mais de estrutura (especificamente um estrutura complexa) que é necessária para a definição não ambígua de funções holomorfos. Um colector de reais bidimensional pode ser transformado em uma superfície de Riemann (geralmente de várias maneiras inequivalent) se e somente se é orientável. Assim, a esfera e toro admitir estruturas complexas, mas o Fita de Möbius, garrafa de Klein e plano projetivo não.

Fatos geométricas sobre superfícies de Riemann são tão "bom" quanto possível, e que muitas vezes fornecem a intuição e motivação para generalizações para outras curvas, tubulações ou variedades. O Riemann-Roch teorema é um excelente exemplo dessa influência.

Definições

Existem várias definições equivalentes de uma superfície de Riemann.

1. Uma superfície de Riemann X é um colector de complexo de complexo dimensão um. Isto significa que o símbolo X representa um bem comportado espaço dotado com uma assim chamada atlas: para cada ponto x ∈ X existe uma ambiente, que se parece com o plano complexo . O mapa de realização da estrutura do plano complexo à superfície de Riemann é chamado gráfico. Dois gráficos que se sobrepõem são necessárias para ser compatível em um certo sentido.
2. Uma superfície de Riemann é um Variedade de Riemann de (real) dimensão dois - donde o nome Riemann superfície, juntamente com uma estrutura conforme. Mais uma vez, distribuidor significa que localmente em qualquer ponto x de X, o espaço é suposto ser como o plano real. O suplemento "Riemann" significa que X é dotado com uma assim chamada G métrica Riemanniana, que permite medir ângulos sobre o manifold. Duas dessas métricas são considerados equivalente se os ângulos que medem são os mesmos. Escolhendo uma métrica, e, portanto, uma classe de equivalência de metrices em que X é o ponto de referência adicional da estrutura conformada.

Uma estrutura complexa dá origem a uma estrutura conformada por escolher o padrão Métrica euclidiana dada no plano complexo e transportá-lo para X por meio dos gráficos.

Exemplos

A esfera de Riemann.

• O plano complexo C é talvez superfície de Riemann o mais básico. O mapa f (z) = z (o mapa de identidade) define um gráfico para C, e {f} um atlas para C. O mapa g (z) = z ^* (a conjugado mapa) também define um gráfico em C e {g} é um atlas para C. O paradas f e g não são compatíveis, de modo que este dota C com duas estruturas de superfície distintas Riemann. De facto, dada uma superfície X Riemann e sua atlas A, o conjugado de Atlas B = {f ^*: f ∈ A} nunca é compatível com A, e dota com X, uma estrutura de Riemann distinta incompatível.

• De um modo análogo, cada subconjunto aberto do plano complexo pode ser visto como uma superfície de Riemann de uma forma natural. Mais geralmente, a cada subconjunto aberto de uma superfície de Riemann é uma superfície de Riemann.

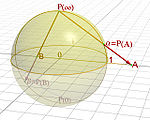
• Seja S = C ∪ {∞} e seja f (z) = z onde z é em S \ {∞} e G (z) = 1 / z onde z é em S \ {0} e 1 / ∞ é definido para ser 0. Em seguida, F e G são gráficos, que são compatíveis, e {f, g} é um atlas de S, S em fazer uma superfície de Riemann. Esta superfície particular é chamado o Riemann esfera porque pode ser interpretado como envolvendo o plano complexo em torno da esfera. Ao contrário do plano complexo, é compacto .

Um toro.

• A teoria das superfícies Riemann compactas podem ser mostrados para ser equivalente à de projectiva curvas algébricas que são definidos sobre os números complexos e não singular. Por exemplo, o toro C / (Z + τ Z), onde τ é um número complexo não real, corresponde, por meio do Função elíptica de Weierstrass associado ao treliça Z + τ Z, para uma curva elíptica dada por uma equação

y ² = x ³ + ax + b.

Tori são as únicas superfícies de Riemann de um género, superfícies de maior géneros g são fornecidos pela superfícies hiperelípticos

y ² = P (x),

onde P é um complexo polinômio de grau 2 g 1.

• Exemplos importantes de superfícies de Riemann não-compactas são fornecidos por continuação analítica.

Outras definições e propriedades

Como acontece com qualquer mapa entre variedades complexas, uma função f: M → N entre duas superfícies de Riemann M e N é chamado holomorphic se para cada gráfico g no atlas de M e cada gráfico h no atlas de N, o mapa h o f o g ^-1 é holomorfa (como uma função de C para C) onde ele está definido. A composição de dois mapas holomorfas é holomorfa. As duas superfícies de Riemann M e N são chamados biholomorphic (ou conformemente equivalente a enfatizar o ponto de vista conformal) se existe uma função holomórfica bijectiva de M para N cujo inverso também é holomórfica (verifica-se que esta última condição é automático e pode, portanto, ser omitida). Duas superfícies de Riemann conformalmente equivalentes são para todos os efeitos práticos idênticos.

Orientabilidade

Notamos no preâmbulo que todas superfícies de Riemann, como todas as variedades complexas, são orientável como um colector de real. A razão é que, para gráficos complexos e f g com função de transição h = f (g ^-1 (z)) podemos considerar h como um mapa de um conjunto aberto de R ² a R ² cujo Jacobian em um ponto z é apenas o mapa linear real dado pela multiplicação do número complexo h '(z). No entanto, o verdadeiro determinante da multiplicação por um número complexo é igual a α | α | ^2, de modo que o Jacobiano de h tem determinante positivo. Consequentemente, o atlas complexo é um atlas orientadas.

Funções

Cada superfície não-compacto Riemann admite funções holomorfas não constantes (com valores em C). Na verdade, todas as superfícies não-compacto Riemann é uma Colector de Stein.

Em contraste, em um compacto Riemann superfície X cada função holomorfa com valor em C é constante devido à princípio máximo. No entanto, existe sempre não constante funções meromorfas (= funções holomorfas com valores na Riemann esfera C ∪ {∞}). Mais precisamente, o campo de função de X é um número finito extensão de C (t), o campo de função em uma variável, ou seja, quaisquer duas funções meromorfas são algebricamente dependente. Esta declaração generaliza para dimensões maiores, consulte Siegel (1955).

Analytic vs. algébrica

O fato acima sobre a existência de funções meromorfas nonconstant pode ser usada para mostrar que qualquer superfície compacta Riemann é uma variedade projetiva, ou seja, pode ser dada por polinômios equações dentro de um espaço projetivo. Na verdade, pode-se mostrar que cada superfície compacta Riemann pode ser incorporado ao plano projetivo complexo. Este é um teorema surpreendente: superfícies de Riemann são dadas por cartas localmente aplicação de patches. Se uma condição global, ou seja, compacidade, é adicionado, a superfície é necessariamente algébrico. Este recurso de superfícies de Riemann permite estudá-los tanto com os meios de analítica ou geometria algébrica. A declaração correspondente para objetos de dimensão superior é falso, ou seja, não são complexas duas dobras compactas que não são algébrica. Por outro lado, cada variedade complexa projetiva é necessariamente algébrica, consulte Teorema de Chow.

Como um exemplo, considere o toro T: = C / (Z + Z τ). A função de Weierstrass 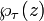pertencente à estrutura Z + Z é um τ meromorfa em função T. Esta função e do seu derivado 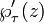gerar o campo função de t. Existe uma equação

onde os coeficientes de g e ₂ g _{de 3} dependem τ, dando assim uma _τ curva elíptica E no sentido da geometria algébrica. A inversão desta é realizada pela j-j invariante (E), que pode ser usado para determinar τ e, portanto, uma toro.

Classificação das superfícies de Riemann

O reino de superfícies de Riemann pode ser dividido em três regimes: superfícies de Riemann hiperbólicas, parabólicas e elípticas. Esta distinção é dada pela uniformização teorema que estabelece que todo superfície de Riemann simplesmente conexa é conformemente equivalente um dos seguintes procedimentos:

• o plano complexo C
• a esfera de Riemann C ∪ {∞}, também denotada P ¹ C

ou

• o aberto disco D: = {z ∈ C: | z | <1} ou equivalentemente a superior semi-plano H: = {z ∈ C: Im (z)> 0}.

De acordo com a equivalência das duas definições dadas acima, o teorema de uniformização também pode ser definida em termos de geometria conforme: a cada Riemann superfície conectado X admite um único completa verdadeira 2-dimensional Riemann métrica com constante curvatura -1, 0 ou 1 induzindo a mesma estrutura conformacional. A superfície X é chamado hiperbólica, parabólica, e elíptica, respectivamente. A existência de três destes tipos paralelos a várias (Não) geometrias euclidianas.

A técnica geral de associar um colector X sua Y tampa universal, e expressando o X original como o quociente de Y pelo grupo de transformações plataforma fornece uma primeira perspectiva sobre superfícies de Riemann.

Elliptic superfícies de Riemann

Por definição, estas são as superfícies com curvatura constante X 1. O Riemann esfera C ∪ {∞} é o único exemplo. ( As curvas elípticas são exemplos de superfícies de Riemann parabólicas A nomeação vem da história:. curvas elípticas são associadas à funções elípticas, que por sua vez aparecem no cálculo do circunferência de elipses ).

Superfícies de Riemann parabólicas

Por definição, estas são as superfícies com curvatura constante X 0. equivalente, pelo teorema de uniformização, a cobertura universal de X tem de ser o plano complexo.

Não há então três possibilidades para X. Pode ser o próprio plano, uma anel, ou um toro

T: = C / (Z ⊕ τ Z).

O conjunto de representantes das classes laterais são chamados domínios fundamentais. Deve ser tomado cuidado na medida em que dois toros são sempre homeomorfos , mas em geral não biholomorphic uns aos outros. Esta é a primeira aparição do problema dos módulos. O módulo de um toro pode ser capturada por um único τ número complexo com parte imaginária positiva. Na verdade, o espaço de módulos marcada ( Teichmüller espaço) do toro é biholomorphic ao semi-plano superior ou equivalente, o disco de unidade aberta.

Hiperbólico superfícies de Riemann

O Riemann superfícies com curvatura -1 são chamados hiperbólica. Este grupo é o "maior" one.

O célebre Riemann Mapeamento teorema indica que qualquer subconjunto estrito simplesmente ligado do plano complexo é biholomorphic à unidade de disco. Portanto, o disco aberta com a Poincaré-métrica de curvatura constante -1 é o modelo local de qualquer superfície hiperbólica Riemann. De acordo com o teorema de uniformização acima, todas as superfícies hiperbólicas são quocientes da unidade de disco.

Os exemplos incluem todas as superfícies com gênero g> 1 tais como curvas de hiper-elípticas.

Para cada superfície hiperbólica Riemann, o grupo fundamental é isomórfico a um Grupo fuchsianas, e, assim, a superfície pode ser modelado por um Fuchsianas modelo H / Γ onde H é a semi-plano superior e Γ é o grupo fuchsianas. O conjunto de representantes das classes laterais de H / Γ são conjuntos regulares livres e pode ser formado em métrica polígonos fundamentais. Estruturas como quociente H / Γ são generalizados para Variedades de Shimura.

Ao contrário de superfícies elípticas e parabólicas, nenhuma classificação das superfícies hiperbólicas é possível. Qualquer subconjunto estrito aberta ligada do avião dá uma superfície hiperbólica; Considere o plano menos um Cantor definido. A classificação é possível para superfícies de tipo finito: aqueles com grupo fundamental finito gerado. Qualquer um destes tem um número finito de módulos e assim um espaço finito Teichmüller dimensional. O problema dos módulos (por resolvido Lars Ahlfors e prorrogado por Lipman Bers) foi para justificar a reivindicação de Riemann que, para uma superfície fechada de gênero g, 3G - 3 parâmetros complexos suficiente.

Quando uma superfície hiperbólica é compacto, então a área total da superfície é 4π (g-1), em que g é a género da superfície; a área é obtida através da aplicação da Gauss-Bonnet para a área do polígono fundamental.

Na arte e literatura

• Um de Os trabalhos de MC Escher, Galeria Print, é colocado para fora em uma grade ciclicamente crescente que tem sido descrito como uma superfície de Riemann.
• Em O romance de Aldous Huxley Brave New World ", Riemann Ténis Surface" é um jogo popular.