Geometria analítica

Coordenadas cartesianas.

Geometria analítica, também chamado de geometria de coordenadas e anteriormente conhecido como geometria cartesiana ou geometria analítica, é o estudo da geometria usando os princípios de álgebra . Que a álgebra dos números reais podem ser empregues para se obter resultados sobre o continuum linear de conta com a geometria Cantor-Dedekind axioma. Normalmente, o sistema de coordenadas cartesianas é aplicada para manipular equações para aviões , linhas, linhas retas, e praças , muitas vezes em dois anos e, por vezes, em três dimensões de medição. Como ensinado nos livros escolares, geometria analítica pode ser explicado de forma mais simples: trata-se preocupado com a definição de formas geométricas de uma forma numérica e extrair informação numérica a partir dessa representação. A saída numérica, no entanto, também pode ser um vector ou uma moldar. Alguns consideram que a introdução da geometria analítica foi o início da moderna matemática .

História

O matemático grego Menaechmus resolveu problemas e provou teoremas usando um método que tinha uma forte semelhança com o uso de coordenadas e tem sido, por vezes, sustentando que não havia geometria analítica. Apolônio de Perga, em Em Determinate Seção tratados problemas de uma forma que pode ser chamado de geometria analítica de uma dimensão; com a questão de encontrar pontos em uma linha que estavam em uma relação com os outros. Apolônio nos Cônicas desenvolvido um método que é tão semelhante à geometria analítica que seu trabalho às vezes é pensado para ter antecipado o trabalho de Descartes por cerca de 1800 anos. A sua aplicação de linhas de referência, um diâmetro e uma tangente é essencialmente diferente do que a nossa utilização moderna de um quadro de coordenadas, em que as distâncias ao longo do diâmetro medido a partir do ponto de tangência são as abcissas, e os segmentos paralelos à tangente e recebido entre o eixo e a curva são ordenadas. Ele desenvolveu ainda mais as relações entre as abscissas e ordenadas correspondentes que são equivalentes às equações retóricas de curvas. No entanto, embora Apolônio chegou perto de desenvolver geometria analítica, ele não consegue fazê-lo desde que ele não leva em conta magnitudes negativas e em todos os casos o sistema de coordenadas foi sobreposta a uma determinada curva a posteriori, em vez de a priori. Isto é, as equações foram determinados por curvas, mas não curvas foram determinadas pelas equações. Coordenadas, variáveis e equações eram noções subsidiárias aplicadas a uma situação geométrica específica.

O século XI persa matemático Omar Khayyam viu uma forte relação entre geometria e álgebra, e estava se movendo na direção certa, quando ele ajudou a fechar a lacuna entre álgebra numérica e geométrica com a solução geométrica da geral equações cúbicas, mas o passo decisivo veio mais tarde com Descartes.

Geometria analítica tem sido tradicionalmente atribuída a René Descartes, que fez progressos significativos com os métodos da geometria analítica quando em 1637 no apêndice intitulado Geometria do discurso intitulado sobre o método para bem conduzir a razão na busca por verdade nas ciências, comumente referido como Discurso do Método. Esta obra, escrita em sua terra natal, francês língua, e seus princípios filosóficos, forneceu a base para o cálculo da Europa.

Abraham de Moivre também foi pioneira no desenvolvimento da geometria analítica. Com a assunção da Cantor-Dedekind axioma, geometria euclidiana, essencialmente, que é interpretável na linguagem da geometria analítica (isto é, cada teorema de um é um teorema da outra), Prova da de Alfred Tarski decidibilidade do campo real, ordenou poderia ser visto como uma prova de que a geometria euclidiana é consistente e decidível.

Temas

Temas importantes da geometria analítica são

• espaço vectorial
• definição do plano
• distância problemas
• o produto de ponto, para obter o ângulo de dois vetores
• o produto cruzado , para obter um vector perpendicular a dois vectores conhecidos (e também o seu volume espacial)
• interseção problemas

Muitos destes problemas envolvem álgebra linear .

Exemplo

Aqui, um exemplo de um problema do Estados Unidos da América Mathematical Talent Search, que pode ser resolvido através de geometria analítica:

Problema: Em um pentágono convexo , Os lados têm comprimentos 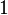, , 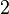, 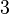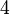E 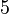, Embora não necessariamente por esta ordem. Deixar 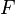, , 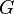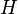E 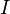ser os pontos médios dos lados , , E , Respectivamente. Deixar 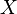ao ponto médio do segmento E 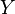ao ponto médio do segmento . O comprimento do segmento 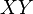é um número inteiro. Encontre todos os valores possíveis para o comprimento do lado .

Solução: Deix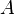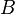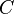e- , , , E ser localizado na , , , E .

Usando o fórmula do ponto médio, os pontos 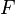, , 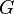, , 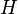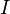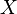E 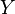está localizado na

, , , , E

Usando a distância fórmula,

e

Desde 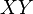tem de ser um número inteiro ,

(Ver aritmética modular ) de modo .

Outros usos

Geometria analítica, para geômetras algébricos, é também o nome para a teoria da (real ou) variedades complexas e os espaços analíticos mais gerais definidos localmente pelo desaparecimento de funções analíticas de várias variáveis complexas (ou, por vezes, os reais). Ela está intimamente ligada à geometria algébrica, especialmente através do trabalho de Jean-Pierre Serre em GAGA.