
Álgebra
Fundo para as escolas Wikipédia
Esta seleção é feita para as escolas de caridade infantil leia mais . Uma boa maneira de ajudar outras crianças é por patrocinar uma criança
A álgebra é um ramo da matemática relativas ao estudo da estrutura , relação e quantidade . O nome é derivado do tratado escrito em árabe pelo Persa matemático, astrônomo, astrólogo e geógrafo, Muhammad bin Musa al-Khwarizmi intitulado Kitab al-Jabr wa-l-muqabala (que significa " O Livro Compendious sobre Cálculo de Conclusão e Balanceamento "), que forneceu as operações simbólicas para a solução sistemática de linear e equações de segundo grau .
Juntamente com a geometria , análise , análise combinatória e teoria dos números , álgebra é um dos principais ramos da matemática . álgebra elementar é muitas vezes parte do currículo no ensino secundário e fornece uma introdução às ideias básicas da álgebra, incluindo efeitos da adição e multiplicação números , o conceito de variáveis, definição de polinômios , juntamente com fatoração e determinar a sua raízes.
A álgebra é muito mais ampla do que a álgebra elementar e pode ser generalizada. Além de trabalhar diretamente com os números, álgebra abrange trabalhar com símbolos, variáveis, e conjunto elementos. Adição e multiplicação são vistos como geral operações, e suas definições precisas levar a estruturas como grupos , anéis e campos.
Classificação
Álgebra pode ser dividido mais ou menos nas seguintes categorias:
- Álgebra elementar , em que as propriedades de operações no sistema de números reais são registradas através de símbolos como "lugar titulares" para denotar constantes e variáveis e as regras que regem expressões matemáticas e equações que envolvem esses símbolos são estudados (note que este geralmente inclui o tema de cursos chamados de álgebra intermediário e álgebra faculdade), também chamado de segundo ano e terceiro ano de álgebra;
- Álgebra abstrata , às vezes também chamado de álgebra moderna, em que estruturas algébricas tais como grupos , anéis e campos são axiomaticamente definido e investigados; isto inclui, entre outras áreas,
- Álgebra linear , em que as propriedades específicas de espaços vetoriais são estudados (incluindo matrizes );
- Álgebra universal, em que as propriedades comuns a todas as estruturas algébricas são estudados.
- Teoria dos números algébricos, em que as propriedades dos números são estudados através de sistemas algébricos. A teoria dos números inspirou grande parte da abstração original na álgebra.
- Geometria Algébrica no seu aspecto algébrico.
- Combinatória algébricas , nos quais métodos algébricos abstratos são usados para estudar questões combinatórias.
Em algumas indicações de estudos avançados, sistemas algébricos axiomático tais como grupos, anéis, campos e álgebras sobre um campo são investigadas na presença de um geométrico estrutura (a métrica ou uma topologia ) que é compatível com a estrutura algébrica. A lista inclui uma série de áreas de análise funcional:
- Espaços linear normalizado
- Espaços de Banach
- Espaços de Hilbert
- Álgebras de Banach
- Álgebras normados
- Álgebras topológicas
- Grupos topológicos
Álgebra elementar
Álgebra elementar é a forma mais básica de álgebra. É ensinado aos estudantes que se presume ter nenhum conhecimento de matemática para além dos princípios básicos da aritmética . Na aritmética, apenas números e suas operações aritméticas (como +, -, ×, ÷) ocorrer. Em álgebra, os números são frequentemente designados por símbolos (tais como A, X, ou Y). Isto é útil porque:
- Ele permite que a formulação geral da leis aritméticas (tais como a + b = b + a para todo a e b), e, portanto, é o primeiro passo para uma exploração sistemática das propriedades do sistema de números reais .
- Ele permite que a referência aos números de "desconhecidos", a formulação de equações eo estudo de como resolver estes (por exemplo, "Encontrar um número x tal que x 3 + 1 = 10").
- Ele permite a formulação de funcionais relacionamentos (como "Se você vender x bilhetes, então seu lucro será de 3 x - 10 dólares, ou f (x) = x 3 - 10, onde f é a função, e x é o número ao qual a função é aplicada. ").
Polinômios
Um polinômio é uma expressão que é construída a partir de um ou mais variáveis e constantes, utilizando apenas as operações de adição, subtração, multiplicação e (onde repetiu multiplicação da mesma variável é standardly denotado como exponenciação com um número inteiro expoente positivo constante). Por exemplo,  é um polinômio no único x variável.
é um polinômio no único x variável.
Uma importante classe de problemas em álgebra é factorization de polinómios, isto é, que expressa um dado polinomial como um produto de outros polinomiais. O exemplo acima polinomial pode ser contabilizado como  A classe relacionada de problemas é encontrar expressões algébricas para a raízes de um polinômio em uma única variável.
A classe relacionada de problemas é encontrar expressões algébricas para a raízes de um polinômio em uma única variável.
Abstract álgebra
Abstract álgebra estende os conceitos familiares encontrados em álgebra elementar e aritmética de números para conceitos mais gerais.
Conjuntos: Ao invés de apenas considerar os diferentes tipos de números , abstrato álgebra lida com o conceito mais geral de conjuntos: uma coleção de todos os objetos (chamada elementos) selecionados pela propriedade, específicos para o conjunto. Todas as coleções dos tipos familiares de números são conjuntos. Outros exemplos de conjuntos incluem o conjunto de todos os dois-por-dois matrizes , o conjunto de todas as de segundo grau polinômios (ax 2 + bx + c), o conjunto de todas as duas dimensões vetores no plano, e os vários grupos finitos, tais como os grupos cíclicos que são o grupo de inteiros módulo n. A teoria dos conjuntos é um ramo da lógica e não tecnicamente um ramo da álgebra.
Operações binárias: A noção de adição (+) é abstraída para dar uma operação binária, * dizer. A noção de operação binária não tem sentido sem o conjunto em que a operação está definida. Por dois elementos A e B em um conjunto S a * b dá outro elemento do conjunto; esta condição é chamada . encerramento adição (+), subtração (-), multiplicação (×) e divisão (÷) podem ser operações binárias, quando definido em diferentes conjuntos, como é adição e multiplicação de matrizes, vetores e polinômios.
Elementos de identidade: os números zero e um são abstraídos para dar a noção de um elemento de identidade para uma operação. Zero é o elemento de identidade para adição e um é o elemento neutro para a multiplicação. Para um operador binário geral * a identidade elemento e deve satisfazer um * e = A e E * a = a. Isso vale para a adição como um + 0 = a 0 e + a = a multiplicação e a × 1 = a 1 × e a = a. No entanto, se tomarmos os números naturais positivos e além disso, não há nenhum elemento de identidade.
Elementos inversos: os números negativos dar origem ao conceito de elementos inversos. Para além disso, o inverso de uma -a é, para a multiplicação e o inverso é 1 / a. Um elemento inverso geral a -1 deve satisfazer a propriedade de que a * a -1 = e e um -1 * A = E.
Associatividade : Adição de números inteiros tem uma propriedade chamada associatividade. Ou seja, o agrupamento dos números a ser adicionada não afecta a soma. Por exemplo: (2 + 3) + 4 + 2 = (3 + 4). Em geral, este torna-se (a * b) * c = a * (b * c). Esta propriedade é compartilhada pela maioria dos operações binárias, mas não subtração ou divisão ou multiplicação octonion.
Comutatividade : Adição de inteiros também tem uma propriedade chamada comutatividade. Isto é, a ordem dos números a ser adicionada não afecta a soma. Por exemplo: 2 + 3 + 2 = 3. Em geral, este torna-se a * b = b * um. Apenas algumas operações binárias têm essa propriedade. Ele vale para os inteiros com adição e multiplicação, mas não vale para a multiplicação de matrizes ou multiplicação quaternion.
Grupos-estruturas de um conjunto com uma única operação binária
Combinando os conceitos acima dá uma das estruturas mais importantes em matemática: um grupo . Um grupo é uma combinação de um conjunto de S e uma única operação binária "*", definido em qualquer maneira que você escolher, mas com as seguintes propriedades:
- Um elemento de identidade e existe, de tal forma que para cada membro de um S, e * um * e um e são ambos idêntico a um.
- Cada elemento tem um inverso: para todos os membros de um S, existe um membro de uma tal forma que uma -1 * -1 e uma -1 * A são ambos idênticos ao elemento de identidade.
- A operação é associativa: se a, b e c são membros de S, então (a * b) * c é idêntico a um * (b * c).
Se um grupo é também conmutativo - isto é, por quaisquer dois membros um de S e b, a * b é igual a b * -, então o grupo é dito ser Abelian.
Por exemplo, o conjunto dos números inteiros no âmbito da operação de adição é um grupo. Neste grupo, o elemento de identidade é 0 e o inverso de qualquer elemento é uma sua negação, - um. O requisito associamento é cumprida, porque para quaisquer inteiros a, b e c, (a + b) + c = a + (b + c)
Os diferentes de zero números racionais formam um grupo sob a multiplicação. Aqui, o elemento de identidade é 1, desde 1 × a = a × 1 = a para qualquer número racional a. O inverso de a é 1 / a, uma vez que uma × 1 / a = 1.
Os inteiros sob a operação de multiplicação, no entanto, não formam um grupo. Isto é porque, em geral, o inverso multiplicativo de um número inteiro não é um número inteiro. Por exemplo, é um número inteiro 4, mas o seu inverso multiplicativo é de 1/4, o que não é um número inteiro.
A teoria dos grupos é estudada em teoria de grupos . Um resultado importante nesta teoria é a classificação dos grupos finitos simples, publicados principalmente entre cerca de 1955 e 1983, que é pensado para classificar toda a finito grupos simples em cerca de 30 tipos básicos.
| Exemplos | ||||||||||
| Set: | Números naturais 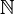 | Inteiros 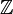 | Números racionais 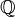 (Também verdadeiro (Também verdadeiro 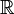 e complexo e complexo 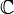 números) números) | Inteiros mod 3: {0,1,2} | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Operação | + | × (w / o zero) | + | × (w / o zero) | + | - | × (w / o zero) | ÷ (w / o zero) | + | × (w / o zero) |
| Fechadas | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim |
| Identidade | 0 | 1 | 0 | 1 | 0 | N / D | 1 | N / D | 0 | 1 |
| Inverso | N / D | N / D | -a | N / D | -a | N / D |  | N / D | 0,2,1, respectivamente | NA, 1, 2, respectivamente |
| Associativo | Sim | Sim | Sim | Sim | Sim | Não | Sim | Não | Sim | Sim |
| Comutativa | Sim | Sim | Sim | Sim | Sim | Não | Sim | Não | Sim | Sim |
| Estrutura | monoid | monoid | Grupo abeliano | monoid | Grupo abeliano | quasigroup | Grupo abeliano | quasigroup | Grupo abeliano | Grupo abeliano (  ) ) |
Semigrupos, quasigroups, e monoids são estruturas semelhantes a grupos, mas mais geral. Eles compreendem um conjunto e uma operação binária fechado, mas não necessariamente satisfazer as outras condições. A semigroup tem uma operação binária associativa, mas pode não ter um elemento de identidade. A monoid é um semigrupo que tem uma identidade, mas pode não ter uma inversa para cada elemento. A quasigroup satisfaz o requisito de que qualquer elemento pode ser transformado em qualquer outro por uma única pré ou pós-operação; no entanto, a operação binária pode não ser associativa. Todos são instância grupóides, estruturas com uma operação binária sobre a qual são impostas há outras condições.
Todos os grupos são monoids, e todos os monoids são semigroups.
Anéis e campos-estruturas de um conjunto com duas operações binárias particulares, (+) e (x)
Grupos só tem uma operação binária. Para explicar totalmente o comportamento dos diferentes tipos de números, estruturas com dois operadores precisam ser estudados. A mais importante delas são anéis, e campos.
Distributividade generalizou a lei distributiva para os números, e especifica a ordem em que os operadores devem ser aplicados, (o chamado precedência). Para os números inteiros (a + b) x c = a + b x c x c e c x (a + b) = C a + c × × b, e x é dito ser distributiva sobre +.
A anel tem duas operações binárias (+) e (x), com mais de distributiva × +. Sob o primeiro operador (+) forma um grupo abeliano. De acordo com o segundo operador (x) é associativo, mas não precisa de ter uma identidade, ou inversa, de modo a divisão não é permitido. O elemento de identidade aditivo (+) é escrito como 0 e o inverso de um aditivo é escrita como: - uma.
Os inteiros são um exemplo de um anel. Os inteiros têm propriedades adicionais que tornam uma domínio integral.
A campo é um anel com a propriedade adicional de que todos os elementos excluindo 0 formam um grupo abeliano sob ×. O (x) de identidade multiplicativo é escrito como um eo inverso multiplicativo de um está escrito como uma -1.
Os números racionais, os números reais e números complexos são exemplos de campos.
Objetos chamados álgebras
A palavra álgebra também é utilizado para vários estruturas algébricas :
- Álgebra sobre um campo ou, mais geralmente Álgebra sobre um anel
- Álgebra sobre um conjunto
- Álgebra booleana
- F-álgebra e F-coalgebra em teoria da categoria
- Sigma-álgebra
História

As origens da álgebra pode ser rastreada à antiga Babilônios, que desenvolveram um avançado sistema de aritmética com os quais eles foram capazes de fazer cálculos em uma forma algébrica. Com a utilização deste sistema foram capazes de aplicar fórmulas e calcular soluções para valores desconhecidos para uma classe de problemas tipicamente resolvidos hoje, usando equações lineares , equações de segundo grau , e equações lineares indeterminados. Em contraste, a maioria Egípcios desta época, e mais indiano , Grego e Matemáticos chineses no primeiro milénio BC, normalmente resolvido por estas equações geométricas métodos, tais como os descritos na Rhind Papyrus, Sulba Sutras, Elementos de Euclides , e Os Nove Capítulos da Arte Matemática. O trabalho geométrico dos gregos, tipificado no Elements, forneceu a estrutura para generalizar fórmulas para além da solução de problemas específicos em sistemas mais gerais de afirmar e resolução de equações.
Mais tarde, os matemáticos indianos desenvolvido métodos algébricos para um elevado grau de sofisticação. Embora Diofanto e os babilônios usado principalmente métodos ad hoc especiais para resolver equações, Brahmagupta foi o primeiro a resolver equações usando métodos gerais. Ele resolveu as equações indeterminadas lineares, equações de segundo grau, de segunda ordem equações indeterminadas e equações com múltiplas variáveis.
A palavra "álgebra" é nomeado após o árabe palavra "al-jabr" do título do livro al-Kitab al-muḫtaṣar fī Hisab al-Gabr wa-l-muqabala, significando O livro de sumários de Cálculo por Transposição e Redução, um livro escrito pelo Matemático persa Al-Khwarizmi em 820. A palavra Al-Jabr significa "reunião". O matemático helenístico Diofanto tem sido tradicionalmente conhecido como "o pai da álgebra", mas agora existe debate quanto à possibilidade ou não de Al-Khwarizmi deve levar esse título. Aqueles que apoiam ponto Al-Khwarizmi para o fato de que muito do seu trabalho no redução ainda está em uso hoje e que lhe deu uma explicação exaustiva de resolver equações de segundo grau. Aqueles que apoiam Ponto Diofanto ao fato de que a álgebra encontrados em Al-Jabr é mais fundamental do que a álgebra encontrado em Aritmética e que Arithmetica é sincopado enquanto Al-Jabr é totalmente retórica. Outro matemático persa, Omar Khayyam, desenvolvido geometria algébrica e encontrou a solução geométrica geral da equação cúbico. Os matemáticos indianos Mahavira e Bhaskara II, eo matemático chinês Zhu Shijie, resolvido vários casos de cúbico, quartic, quintic e de ordem superior polinomiais equações.
Outro evento chave no desenvolvimento da álgebra foi a solução algébrica geral das equações cúbicas e quárticas, desenvolvido em meados do século 16. A idéia de um determinante foi desenvolvido por Matemático japonês Kowa Seki no século 17, seguido por Gottfried Leibniz dez anos depois, com a finalidade de sistemas de equações lineares simultâneas, em resolver as matrizes . Gabriel Cramer também fez alguns trabalhos sobre as matrizes e determinantes no século 18. Abstract álgebra foi desenvolvido no século 19, inicialmente focando no que hoje é chamado de teoria de Galois , e em questões construtibilidade.
As etapas do desenvolvimento da álgebra simbólica são mais ou menos da seguinte forma:
- Álgebra retórico, que foi desenvolvido pelos babilônios e permaneceu dominante até o século 16;
- Álgebra geométrica construtiva, que foi enfatizado pelo Védicos matemáticos gregos e indianos clássicos;
- Sincopado álgebra, como desenvolvido pela Diofanto, Brahmagupta eo Bakhshali Manuscrito; e
- Álgebra simbólica, que foi iniciada por Abu al-Hasan ibn Ali al-Qalasādī e vê o seu ápice na obra de Gottfried Leibniz .

Uma linha do tempo da evolução algébricas-chave são as seguintes:
- Por volta de 1800 aC: O Old babilônico Strassburg tablet busca a solução de uma equação quadrática elíptica.
- Por volta de 1600 aC: O Plimpton 322 tablet dá uma tabela de Trios pitagóricos em babilônico Escrita cuneiforme.
- Por volta de 800 aC: o matemático indiano Baudhayana, em sua Baudhayana Sulba Sutra, descobre trios pitagóricos algebricamente, encontra soluções geométricas das equações lineares e equações de segundo grau do machado formas 2 = C e ax 2 + bx = c, e encontra dois conjuntos de soluções positivas para um conjunto de simultânea Equações diofantinas.
- Por volta de 600 aC: o matemático indiano Apastamba, em sua Apastamba Sulba Sutra, resolve a equação linear geral e utiliza equações diofantinas simultâneas com até cinco incógnitas.
- Por volta de 300 aC: No Livro II dos seus Elementos, Euclides dá uma construção geométrica com ferramentas euclidianas para a solução da equação quadrática para as raízes reais positivos. A construção deve-se à Escola Pitagórica da geometria.
- Por volta de 300 aC: A construção geométrica para a solução do cúbica é procurado (duplicando o problema cubo). É agora bem conhecido que o cúbico geral não tem essa solução usando ferramentas Euclidiana .
- Por volta de 100 aC: equações algébricas são tratados no livro matemática chinesa Jiuzhang suanshu (Os Nove Capítulos da Arte Matemática), que contém soluções de equações lineares resolvido usando o Estado de dupla posição falsa, soluções geométricas das equações de segundo grau, e as soluções de matrizes equivalentes ao método moderno, para resolver sistemas de equações lineares.
- Por volta de 100 aC: O Bakhshali Manuscrito escrito em Índia antiga utiliza uma forma de notação algébrica usando as letras do alfabeto e outros sinais, e contém equações cúbicas e quárticas, soluções algébricas de equações lineares com até cinco incógnitas, a fórmula algébrica geral para a equação quadrática, e soluções de equações indeterminadas e de equações simultâneas.
- Por volta de 150 dC: Heron de Alexandria trata equações algébricas em três volumes de matemática.
- Cerca de 200: Diofanto, que viveu no Egito e é muitas vezes considerado o "pai da álgebra", escreve seu famoso Aritmética, um trabalho com soluções de equações algébricas e sobre a teoria dos números.
- 499: o matemático indiano Aryabhata, em seu tratado Aryabhatiya, obtém soluções de números inteiros para equações lineares por um método equivalente ao moderno, descreve a solução integral geral da equação linear indeterminado e dá soluções de equações lineares simultâneas indeterminados.
- Cerca de 625: matemático chinês Wang Xiaotong encontra soluções numéricas de equações cúbicas.
- 628: o matemático indiano Brahmagupta, em seu tratado Brahma Cuspe Siddhanta, inventa o chakravala método de resolver equações de segundo grau indeterminados, incluindo A equação de Pell, e dá regras para a resolução de equações linear e quadrática.
- 820: A palavra é derivada da álgebra operações descritas no tratado escrito pelo Matemático persa Muhammad ibn Musa al-Ḵwārizmī intitulado Al-Kitab al-Jabr wa-l-muqabala (que significa "O Livro Compendious sobre Cálculo de Conclusão e balanceamento") na solução sistemática de linear e equações de segundo grau . Al-Khwarizmi é muitas vezes considerado como o "pai da álgebra", grande parte cujas obras sobre a redução foi incluído no livro e adicionado a muitos métodos que temos na álgebra agora.
- Cerca de 850: Matemático persa al-Mahani concebeu a idéia de reduzir problemas geométricos, tais como duplicação do cubo para os problemas de álgebra.
- Cerca de 850: matemático indiano Mahavira resolve várias equações de segundo grau, cúbicos, quárticas, quintic e de ordem superior, bem como quadrática indeterminado, equações cúbicas e de ordem superior.
- Cerca de 990: Persa Abu Bakr al-Karaji, em seu tratado al-Fakhri, desenvolve álgebra, alargando a metodologia de Al-Khwarizmi para incorporar poderes integrais e raízes integrantes de quantidades desconhecidas. Ele substitui operações geométricas da álgebra com operações aritméticas modernos, e define o monomios x, x 2, x 3, ... e 1 / x, 1 / x 2, 1 / x 3, ... e dá regras para os produtos de quaisquer dois destes.
- Circa 1050: matemático chinês Jia Xian encontra soluções numéricas de equações polinomiais.
- 1072: Matemático persa Omar Khayyam desenvolve geometria algébrica e, no Tratado sobre a Demonstração de Problemas de Álgebra, dá uma classificação completa de equações cúbicos com soluções geométricas gerais encontrados por meio de interseção seções cônicas.
- 1114: o matemático indiano Bhaskara, em sua Bijaganita (Álgebra), reconhece que um número positivo tem tanto um positivo e negativo raiz quadrada , e resolve várias equações polinomiais cúbicos, quartic e de ordem superior, bem como a equação quadrática indeterminant geral.
- 1202: Álgebra é introduzido para a Europa , em grande parte através do trabalho de Leonardo Fibonacci de Pisa em seu trabalho Liber Abaci.
- Circa 1300: matemático chinês Zhu Shijie lida com álgebra polinomial, resolve equações, equações simultâneas e equações com até quatro incógnitas, e numericamente resolve alguns quartic, quintic e de ordem superior equações polinomiais.
- Circa 1400: o matemático indiano Madhava de Sangamagramma encontra métodos iterativos para solução aproximada de equações não-lineares.
- Circa 1450: matemático árabe Abu al-Hasan ibn Ali al-Qalasādī levou "os primeiros passos para a introdução de simbolismo algébrico. "Ele representou símbolos matemáticos usando personagens do Alfabeto árabe.
- 1535: Nicolo Fontana Tartaglia e outros matemáticos em Itália resolvido de forma independente a equação cúbica geral.
- 1545: Girolamo Cardano publica Ars magna - A grande arte que dá a solução de Fontana com a equação quártica geral.
- 1572: Rafael Bombelli reconhece as raízes complexas do cúbica e melhora a notação atual.
- 1591: Francois Viète desenvolve uma melhor notação simbólica para vários poderes de um desconhecido e usa vogais e consoantes para incógnitas para constantes em artem Em analyticam Isagoge.
- 1631: Thomas Harriot em uma publicação póstuma usa a notação exponencial e é o primeiro a usar símbolos para indicar "menos do que" e "maior que".
- 1682: Gottfried Wilhelm Leibniz desenvolve sua noção de manipulação simbólica com regras formais que ele chama de characteristica generalis.
- 1680: matemático japonês Kowa Seki, em seu método de resolver os problemas dissimuladas, descobre o determinante , e Números de Bernoulli.
- 1750: Gabriel Cramer, em seu tratado Introdução à análise de curvas algébricas, afirma Regra e estudos de Cramer algébrica curvas, matrizes e determinantes.
- 1824: Niels Henrik Abel provou que a equação geral do quinto grau é insolúvel por radicais.
- 1832: teoria de Galois é desenvolvido por Evariste Galois em seu trabalho em álgebra abstrata.
