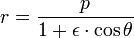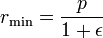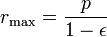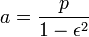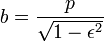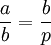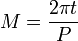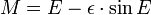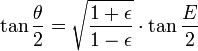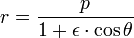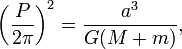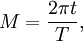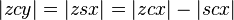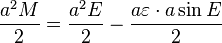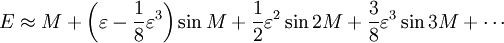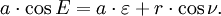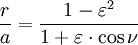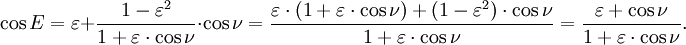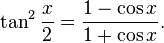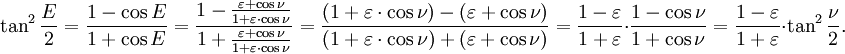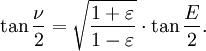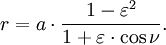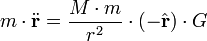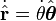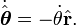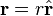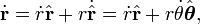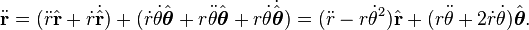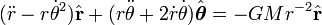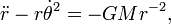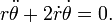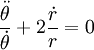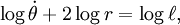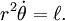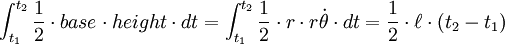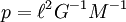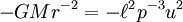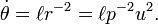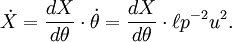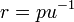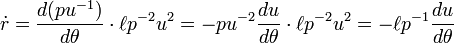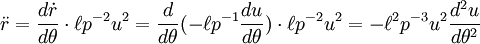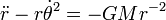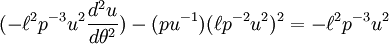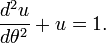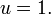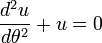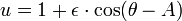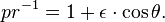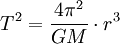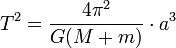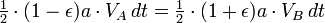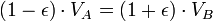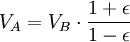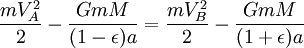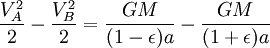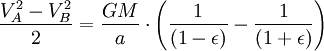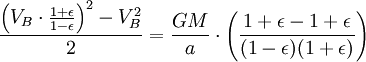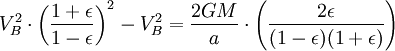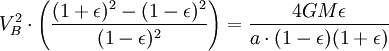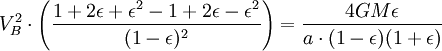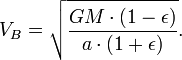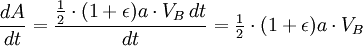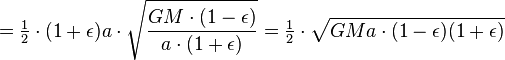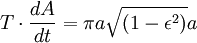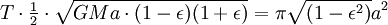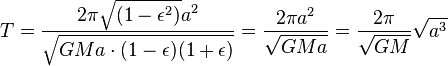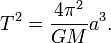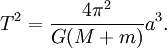Leis de Kepler

Assuntos Relacionados: Matemática

Informações de fundo

Crianças SOS oferecem um download completo desta seleção para as escolas para uso em escolas intranets. Clique aqui para saber mais sobre apadrinhamento de crianças.

Ilustração de três leis de Kepler com duas órbitas planetárias. (1) As órbitas são elípticas, com os pontos focais f1 e f2 para o primeiro planeta e F1 e F3 para o segundo planeta. O sol está colocado no ponto focal f1. (2) Os dois sectores sombreadas A1 e A2 têm a mesma área de superfície e o tempo para a cobrir planeta um segmento A1 é igual ao tempo para cobrir segmento A2. 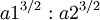(3) Os tempos totais de órbita para um planeta planeta e 2 têm um rácio $a1 ^ {3/2}: a2 ^ {3/2}$ .

Em astronomia , Leis de Kepler do Movimento Planetário são três leis matemáticas que descrevem o movimento dos planetas no Sistema Solar . Alemão matemático e astrônomo Johannes Kepler ( 1571- 1630) descobri-los.

Kepler estudou o observações do astrônomo dinamarquês preciso legendarily Tycho Brahe. Por volta de 1605, Kepler descobriu que as observações de Brahe de posições dos planetas seguido três leis matemáticas relativamente simples.

As leis de Kepler desafiou astronomia e física aristotélica e ptolemaica. Sua afirmação de que a Terra se movia, seu uso de elipses em vez de epiciclos, e sua prova de que as velocidades dos planetas variados, mudou astronomia e física . No entanto, a explicação física do comportamento dos planetas veio quase um século mais tarde, quando Isaac Newton foi capaz de deduzir as leis de Kepler a partir do próprio Newton leis do movimento e sua lei da gravitação universal, usando a invenção do cálculo . Outros modelos de gravitação daria resultados empiricamente falsos.

Três leis de Kepler são:

O órbita de cada planeta é uma elipse com o sol em um dos focos. Uma elipse é caracterizado por seus dois pontos focais; veja a ilustração. Assim, Kepler rejeitou a aristotélica antigo, ptolomaico e copernicano crença em movimento circular.
A linha de aderir a um planeta eo Sol varre áreas iguais durante os intervalos de tempo iguais conforme o planeta percorre sua órbita. Isto significa que o planeta viaja mais rápido, enquanto perto do sol e retarda quando está mais distante do sol. Com sua lei, Kepler destruiu a teoria astronômica aristotélica de que os planetas têm uniforme velocidade .
O praças da períodos orbitais de planetas são diretamente proporcional ao cubos do semi-eixos maiores (a "metade do comprimento" da elipse) de suas órbitas. Isto significa que não só têm órbitas grandes períodos mais longos, mas também que a velocidade de um planeta numa órbita maior é inferior ao de um órbita mais pequeno.

As leis de Kepler são formuladas abaixo, e são derivadas de leis de Newton, usando heliocêntrico coordenadas polares 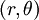$\ (R, \ teta)$ . No entanto, as leis de Kepler, alternativamente, pode ser formulado e derivados utilizando coordenadas cartesianas .

Descrição matemática

Primeira lei

A primeira lei de Kepler

A primeira lei diz: "O órbita de cada planeta é uma elipse com o sol em um dos focos. "

A matemática da elipse é a seguinte.

A equação é

$r = \ frac {p} {1+ \ epsilon \ cdot \ cos \ theta}$

onde (r, θ) são coordenadas polares heliocêntricas para o planeta, o símbolo p representa o recto semi-latus , e é o ε excentricidade, que é maior do que ou igual a zero, e menos do que um.

Para θ = 0 o planeta é a periélio a distância mínima:

$r_ \ mathrm {min} = \ frac {p} {1+ \ epsilon}$

para θ = 90 °: R = p, e para θ = 180 ° o planeta é a afélio a máxima distância:

$r_ \ mathrm {max} = \ frac {p} {1- \ epsilon}$

O semi-eixo maior é a média aritmética entre r r _min e _máx:

$a = \ frac {p} {1- \ epsilon ^ 2}$

O semi-eixo menor é a média geométrica entre _Rmin e _Rmax:

$b = \ frac p {\ sqrt {1- \ epsilon ^ 2}}$

e também o é média geométrica entre o semi-eixo maior e o recto semi latus:

$\ Frac uma b = \ frac b p$

Segunda lei

Ilustração da segunda lei de Kepler.

A segunda lei: "A linha de aderir a um planeta eo Sol varre áreas iguais durante os intervalos de tempo iguais. "

Esta é também conhecida como a lei de áreas iguais. É uma consequência directa da lei da conservação do momento angular ; veja a derivação abaixo.

Suponha que um planeta leva um dia para viajar de ponto A ao B. As linhas do Sol para A e B, em conjunto com a órbita do planeta, vai definir uma (aproximadamente triangular área). Essa mesma quantidade de área será formada todos os dias, independentemente de onde em sua órbita do planeta é. Isto significa que o planeta se move mais rapidamente quando está mais perto do sol.

Isso ocorre porque a gravidade do Sol acelera o planeta à medida que cai em direção ao sol, e desacelera-lo no caminho de volta para fora, mas Kepler não sabia que a razão.

As duas leis permitida Kepler para calcular a posição, (r, θ), do planeta, com base no tempo desde periélio, t, eo período orbital, P. O cálculo é feito em quatro passos.

1. Calcule a média anomalia M a partir da fórmula

$M = \ frac {2 \ pi t} {P}$

2. Calcule o excêntrico anomalia E por resolver numericamente a equação de Kepler:

$\ M = E- \ epsilon \ cdot \ pecado E$

3. Calcule o verdadeiro θ anomalia pela equação:

$\ Tan \ frac \ theta 2 = \ sqrt {\ frac {1+ \ epsilon} {1- \ epsilon}} \ cdot \ tan \ frac E 2$

4. Calcule a distância r heliocêntrica da primeira lei:

$r = \ frac {p 1+ \ epsilon \ cdot \ cos \ theta}$

A prova deste procedimento é mostrado abaixo.

Terceira lei

A terceira lei: "O praças da períodos orbitais de planetas são diretamente proporcional ao cubos do semi-eixo maior das órbitas. "Deste modo, não só o comprimento da órbita aumentar com a distância, a velocidade orbital diminui, de modo que o aumento da período orbital é mais do que proporcional.

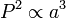
$P ^ 2 \ propto um ^ 3$

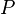$P$ = Período orbital de planeta

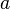$um$ = Semi-eixo maior da órbita

Portanto, a expressão P ² · um ^-3 tem o mesmo valor para todos os planetas do Sistema Solar , pois tem para Terra . Quando certas unidades são escolhidos, nomeadamente P é medido em siderais anos e uma em unidades astronômicas, P ² · um ^-3 tem o valor de 1 para todos os planetas do Sistema Solar.

Em Unidades SI: 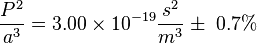$\ Frac {P ^ {2}} {a ^ {3}} = 3,00 \ times 10 ^ {- 19} \ frac {s ^ {2}} {m ^ {3}} \ pm \ 0,7% \,$ .

A lei, quando aplicado a órbitas circulares onde a aceleração é proporcional a uma · P ^-2, mostra que a aceleração é proporcional a uma · um ^-3 = ^-2, em conformidade com Lei da gravitação de Newton.

A equação geral, que Kepler não sabia, é

$\ Left ({\ frac {P} {2 \ pi}} \ right) ^ 2 = {a ^ 3 \ over G (M + m)},$

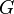onde $G$ é a constante gravitacional, 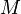$M$ é a massa do Sol, e 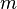$m$ é a massa do planeta. Este último aparece na equação desde a equação de movimento envolve o massa reduzida. Note-se que P é vez por orbitar e P / 2π é tempo por radiano .

Veja os números reais: atributos de planetas maiores.

Esta lei também é conhecida como a lei harmônica.

Posição como uma função de tempo

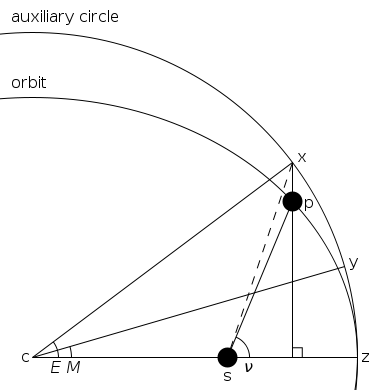
O problema de Kepler assume uma órbita elíptica e os quatro pontos:

s do sol (em um dos focos da elipse);
z o periélio
c o centro da elipse
p o planeta

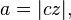$\ A = | CZ |,$ distância do centro para a periélio, o semi-eixo maior,

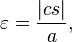$\ \ Varepsilon = {| cs | \ over a},$ a excentricidade,

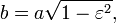$\ B = a \ sqrt {1- \ varepsilon ^ 2},$ semi-eixo menor,

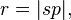$\ R = | sp |,$ a distância do sol ao planeta.

e o ângulo

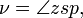$\ Nu = \ ângulo zsp,$ o planeta como visto a partir do sol, a verdadeira anomalia.

O problema é calcular as coordenadas polares (r, ν) do planeta a partir do momento desde periélio, t.

É resolvido nos passos. Kepler começou adicionando círculo auxiliar da órbita (que, com o eixo maior em diâmetro) e definiu os seguintes pontos:

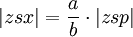
x é a projecção do planeta ao círculo auxiliar; em seguida, a área $| ZSX | = \ frac um b \ cdot | zsp |$
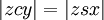
y é um ponto na circunferência auxiliar, tal que a área $\ | Zcy | = | ZSX |$

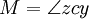$M = \ ângulo zcy$ , Y como visto a partir do centro, o significa anomalia.

A área da sector circular 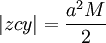$\ | Zcy | = \ frac {a ^ 2 M} 2$ E a área varrida desde periélio,

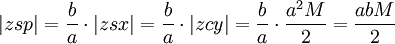$| Zsp | = \ frac ba \ cdot | ZSX | = \ frac ba \ cdot | zcy | = \ frac ba \ cdot \ frac {a ^ 2 M} 2 = \ frac {ab M} {2}$ ,

é de segunda lei de Kepler proporcional ao tempo de periélio. Assim, a média anomalia, M, é proporcional ao tempo desde periélio, t.

$M = {2 \ pi t \ over T},$

em que T é a período orbital.

A média anomalia M é calculado em primeiro lugar. O objectivo é o de calcular o verdadeiro ν anomalia. A função ν = f (H) é, no entanto, não elementar. A solução da Kepler é usar

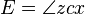$E = \ zcx ângulo$ , X, como visto a partir do centro, o anomalia excêntrica

como uma variável intermédia, e calcular primeiro E em função de M, resolvendo a equação de Kepler abaixo, e em seguida calcular o verdadeiro ν anomalia da anomalia excêntrico E. Aqui estão os detalhes.

$\ | Zcy | = | ZSX | = | zcx | - | scx |$

$\ Frac {a ^ 2 M} 2 = \ frac {a ^ 2} E 2- \ frac {a \ varepsilon \ cdot a \ pecado E} 2$

Divisão por um ² / 2 dá a equação de Kepler

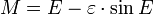$M = E- \ varepsilon \ cdot \ pecado E$ .

O problema é que a equação de Kepler não podem ser reorganizados para isolar E. A função E = f (M) não é uma fórmula elementar. A equação de Kepler é resolvido de forma iterativa ou por um algoritmo ou, como derivado no artigo on-encontrando raiz anomalia excêntrica, por um série infinita

$E \ approx M + \ left (\ varepsilon- \ frac18 \ varepsilon ^ 3 \ right) \ pecado M + \ frac12 \ varepsilon ^ 2 \ pecado 2M + \ frac38 \ varepsilon ^ 3 \ sin 3M + \ cdots$

Para o pequeno ε típica dos planetas (excepto Plutão ), essas séries são bastante precisas com apenas alguns termos.

Tendo calculado a anomalia E excêntrico a partir da equação de Kepler, o próximo passo é calcular o verdadeiro anomalia ν do excêntrico anomalia E.

Nota da geometria do problema que

$a \ cdot \ cos E = a \ cdot \ varepsilon + r \ cdot \ cos \ nu.$

Dividindo por um e inserção da primeira lei de Kepler

$\ \ Ra frac = \ frac {1 \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu}$

para obter

$\ Cos E = \ varepsilon + \ frac {1 \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu} \ cdot \ cos \ nu = \ frac {\ varepsilon \ cdot (1+ \ varepsilon \ cdot \ cos \ nu) + (1- \ varepsilon ^ 2) \ cdot \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu} = \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}.$

O resultado é uma relação entre a anomalia utilizável excêntrico E e o verdadeiro ν anomalia.

Uma forma computacionalmente mais conveniente segue substituindo no identidade trigonométrica:

$\ Tan ^ 2 \ frac {x} {2} = \ frac {1 \ cos x} {1+ \ cos x}.$

Obter

$\ Tan ^ 2 \ frac {E} {2} = \ frac {1 \ cos E} {1+ \ cos E} = \ frac {1 \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}} {1+ \ frac {\ varepsilon + \ cos \ nu} {1+ \ varepsilon \ cdot \ cos \ nu}} = \ frac {(1+ \ varepsilon \ cdot \ cos \ nu) - (\ varepsilon + \ cos \ nu)} {(1+ \ varepsilon \ cdot \ cos \ nu) + (\ varepsilon + \ cos \ nu)} = \ frac {1 \ varepsilon} {1+ \ varepsilon} \ cdot \ frac {1 \ cos \ nu} {1+ \ cos \ nu} = \ frac {1 \ varepsilon} {1+ \ varepsilon} \ cdot \ tan ^ 2 \ frac {\ nu} {2}.$

Multiplicando por (1 + ε) / (1-ε) e tomando a raiz quadrada dá o resultado

$\ Tan \ frac \ NU2 = \ sqrt \ frac {1+ \ varepsilon} {1- \ varepsilon} \ cdot \ tan \ frac E2.$

Foi agora concluído o terceiro passo na conexão entre o tempo e a posição na órbita.

Pode-se até desenvolver uma série computação ν diretamente do M.

O quarto passo é calcular a distância r heliocêntrica do verdadeiro ν anomalia pela primeira lei de Kepler:

$\ R = a \ cdot \ frac {1 \ varepsilon ^ 2} {1+ \ varepsilon \ cdot \ cos \ nu}.$

Derivação das leis de Newton

As leis de Kepler são sobre o movimento dos planetas ao redor do sol, enquanto as leis de Newton mais geralmente são sobre o movimento de partículas do ponto de atrair uns aos outros pela força da gravitação . No caso especial em que existem apenas duas partículas, e um deles é muito mais leve do que a outra, e a distância entre as partículas mantém-se limitado, em seguida, os mais leves movimentos das partículas à volta da partícula pesada como um planeta em torno do sol de acordo com as leis de Kepler , como mostrado abaixo. No entanto as leis de Newton também admitem outras soluções, em que a trajetória da partícula mais leve é uma ou uma parábola hipérbole. Estas soluções mostram que há uma limitação à aplicabilidade da primeira lei de Kepler, que afirma que a trajetória será sempre uma elipse. No caso em que uma partícula não é muito mais leve do que o outro, verifica-se que cada partícula se move em torno de sua comum centro de massa , de modo que a geral dois problema corpo é reduzido para o caso especial em que uma partícula é muito mais leve do que a outra. Enquanto as leis de Kepler são expressas em linguagem geométrica ou como equações que ligam as coordenadas do planeta ea variável tempo com o elementos orbitais, a segunda lei de Newton é uma equação diferencial . Assim, as derivações abaixo envolvem a arte de resolver equações diferenciais. A segunda lei é derivada primeira, como a derivação da primeira lei depende da derivação da segunda lei.

Derivando a segunda lei de Kepler

Lei da Gravitação de Newton diz que "todo objeto no universo atrai todos os outros objetos ao longo de uma linha dos centros dos objetos, proporcional à massa de cada objeto, e inversamente proporcional ao quadrado da distância entre os objetos", e sua segunda lei de movimento diz que "os tempos de massa a aceleração é igual à força." Assim, a massa das vezes planeta o vector de aceleração do planeta é igual à massa do sol vezes a massa do planeta, dividido pelo quadrado da distância, o menos vezes radial vetor unitário, vezes uma constante de proporcionalidade. Isto está escrito:

$m \ cdot \ ddot \ mathbf {r} = \ frac {M \ cdot m} {r ^ 2} \ cdot (- \ hat {\ mathbf {r}}) \ cdot G$

onde um ponto em cima da variável significa diferenciação com respeito ao tempo, e o segundo ponto indica a segunda derivada.

Assume-se que o planeta é muito mais leve do que o sol que a aceleração do sol pode ser negligenciado.

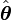$\ Dot \ hat {\ mathbf {r}} = \ dot \ theta \ hat {\ boldsymbol \ theta}$

onde $\ Hat {\ boldsymbol \ theta}$ é o vector de unidade tangencial, e

$\ Dot \ hat {\ boldsymbol \ theta} = - \ dot \ theta \ hat {\ mathbf {r}}.$

Assim, o vector de posição

$\ Mathbf {r} = r \ hat {\ mathbf {r}}$

é diferenciada duas vezes para se obter o vector de velocidade e o vector de aceleração

$\ Dot \ mathbf {r} = \ dot r \ hat \ mathbf {r} + r \ dot \ hat \ mathbf {r} = \ dot r \ hat {\ mathbf {r}} + r \ dot \ theta \ hat {\ boldsymbol \ theta},$

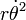$\ Ddot \ mathbf {r} = (\ ddot r \ hat {\ mathbf {r}} + \ dot r \ dot \ hat {\ mathbf {r}}) + (\ dot r \ dot \ theta \ hat {\ boldsymbol \ theta} + r \ ddot \ theta \ hat {\ boldsymbol \ theta} + r \ dot \ theta \ dot \ hat {\ boldsymbol \ theta}) = (\ ddot r - r \ dot \ theta ^ 2) \ hat {\ mathbf {r}} + (r \ ddot \ theta + 2 \ dot r \ dot \ theta) \ hat {\ boldsymbol \ theta}.$

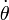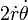Note-se que para a distância constante, $\ R$ , O planeta é sujeito à aceleração centrípeta , $r \ dot \ theta ^ 2$ E para a velocidade angular constante, $\ Dot \ theta$ , O planeta é sujeita à aceleração de Coriolis, $2 \ dot r \ dot \ theta$ .

Inserindo o vector de aceleração em leis de Newton, e dividindo por m, dá o vector equação de movimento

$(\ Ddot r - r \ dot \ theta ^ 2) \ hat {\ mathbf {r}} + (r \ ddot \ theta + 2 \ dot r \ dot \ theta) \ hat {\ boldsymbol \ theta} = -GMr ^ {- 2} \ hat {\ mathbf {r}}$

Igualando componente, temos as duas equações diferenciais ordinárias de movimento, uma para a aceleração radial e uma para a aceleração tangencial:

$\ Ddot r - r \ dot \ theta ^ 2 = -GMr ^ {- 2},$

$r \ ddot \ theta + 2 \ dot r \ dot \ theta = 0.$

A fim de obter a segunda lei de Kepler é apenas necessário a equação de aceleração tangencial. Divida-o por 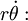$\ R \ dot \ theta:$

$\ Frac {\ ddot \ theta} {\ dot \ theta} 2 \ frac {\ dot r} {r} = 0$

e integrar:

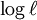$\ Log \ dot \ theta 2 \ log r = \ log \ ell,$

onde $\ Log \ ell$ é um constante de integração, e exponentiate:

$r ^ 2 \ dot \ theta = \ ell.$

Este diz que o momento angular específica 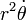$r ^ 2 \ dot \ theta$ é um constante do movimento, mesmo que tanto a distância $\ R$ e o velocidade angular 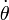$\ Dot \ theta$ variar.

A área varrida para fora a partir de _um tempo t ao tempo t _2,

$\ \ Int_ {t_1} ^ {T_2} \ frac 1 2 \ cdot altura da base \ cdot \ cdot dt = \ int_ {t_1} ^ {T_2} \ frac 1 2 \ cdot r \ cdot r \ dot \ theta \ cdot dt = \ frac 1 2 \ cdot \ ell \ cdot (T_2-t_1)$

depende apenas da duração T ₂ - T _1. Esta é a segunda lei de Kepler.

Derivando a primeira lei de Kepler

A expressão

$p = \ ell ^ 2 G ^ {- 1} M ^ {- 1}$

tem a dimensão de comprimento e é usada para fazer as equações do movimento adimensional. Definimos

$\ U = pr ^ {- 1}$

e obter

$-GMr ^ {- 2} = - \ ell ^ 2 ^ p {- 3} u ^ {2}$

$\ \ Dot \ theta = \ r ell ^ {- 2} = \ ell ^ p {- 2} u ^ 2.$

Diferenciação em relação ao tempo é transformado em diferenciação com respeito ao ângulo:

$\ \ Ponto X = \ frac {dx} {d \ theta} \ cdot \ dot \ theta = \ frac {dx} {d \ theta} \ cdot \ ell ^ p {- 2} u ^ 2.$

Diferenciar

$\ R = pu ^ {- 1}$

duas vezes:

$\ Dot r = \ frac {d (pu ^ {- 1})} {d \ theta} \ cdot \ ell ^ p {- 2} u ^ {2} = -pu ^ {- 2} \ frac {du} {d \ theta} \ cdot \ ell ^ p {- 2} u ^ {2} = - \ ell ^ p {- 1} \ frac {} {du d \ theta}$

$\ Ddot r = \ frac {d \ dot r} {d \ theta} \ cdot \ ell ^ p {- 2} u ^ {2} = \ frac {d} {d \ theta} (- \ ell ^ p { -1} \ frac {} {du d \ theta}) \ cdot \ ell ^ p {- 2} u ^ {2} = - \ ell ^ 2 ^ p {- 3} u ^ {2} \ frac {d u ^ 2} {d \ theta ^ 2}$

Substitua na equação de movimento radial

$\ Ddot r - r \ dot \ theta ^ 2 = -GMr ^ {- 2}$

e obter

$(- \ Ell ^ 2 ^ p {- 3} u ^ 2 \ frac {d ^ 2u} {d \ theta} ^ 2) - (pu ^ {- 1}) (\ ell ^ p {- 2} u ^ 2) ^ 2 = - \ ell ^ 2 ^ p {- 3} u ^ 2$

Divida por 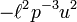$- \ Ell ^ 2 ^ p {- 3} u ^ 2$ para obter uma simples equação diferencial linear não homogénea para a órbita do planeta:

$\ Frac {d ^ 2u} {d \ theta} ^ 2 + u = 1.$

Uma solução óbvia para esta equação é a órbita circular

$\ U = 1.$

Outras soluções são obtidos por adição de soluções ao equação diferencial linear homogêneo com coeficientes constantes

$\ Frac {d ^ 2u} {d \ theta} ^ 2 + u = 0$

Estas soluções são

$\ U = \ epsilon \ cdot \ cos (\ theta-A)$

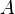onde $\ \ Epsilon$ e $\ A$ são constantes arbitrárias de integração. Assim, o resultado é

$\ U = 1+ \ epsilon \ cdot \ cos (\ theta-A)$

Escolhendo o eixo do tal sistema de coordenadas que 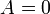$\ A = 0$ E inserção 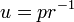$\ U = pr ^ {- 1}$ , Dá:

$\ Pr ^ {- 1} = 1+ \ epsilon \ cdot \ cos \ theta.$

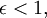Se $\ \ Epsilon <1,$ esta é a primeira lei de Kepler.

A terceira lei de Kepler

Newton usou a terceira lei como um dos elementos de prova utilizados para construir o arcabouço conceitual e matemática de sua Lei da Gravitação. Se tomarmos as leis do movimento de Newton como dadas, e considerar uma planeta hipotético que passa a ser em uma órbita perfeitamente circular de raio r, então temos 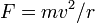$F = mv ^ 2 / r$ para a força do Sol sobre o planeta. A velocidade é proporcional a r / t, o que por a terceira lei de Kepler varia como uma sobre a raiz quadrada de r. Substituindo esta na equação para a força, descobrimos que a força gravitacional é proporcional a um sobre r ao quadrado. Cadeia histórica real de Newton de raciocínio não se sabe com certeza, porque em seus escritos ele tendia a apagar qualquer vestígio de como ele tinha chegado a suas conclusões. Inversão do sentido de raciocínio, podemos considerar isso como uma prova da terceira lei de Kepler baseado na lei da gravidade, e cuidar dos factores de proporcionalidade que foram negligenciadas no argumento acima de Newton, temos:

$T ^ 2 = \ frac {4 \ pi ^ 2} {GM} \ cdot r ^ 3$

onde:

T = planeta de período sideral
r = raio da órbita circular do planeta
G = constante gravitacional
M = massa do sol

Os mesmos argumentos pode ser aplicado a qualquer objecto que orbita qualquer outro objecto. Esta discussão implicitamente assumido que o planeta orbita ao redor do sol estacionário, embora na realidade tanto o planeta eo Sol gira em torno de seu centro de massa comum. Newton reconheceu isto, e modificou esta terceira lei, observando que o período também é afetada pelo corpo em órbita em massa . No entanto normalmente o corpo central é muito mais massiva que a massa do corpo em órbita pode ser ignorado. Newton também mostrou que, no caso de uma órbita elíptica, o semimaior eixo pode ser substituído para o raio. O resultado mais geral é:

$T ^ 2 = \ frac {4 \ pi ^ 2} {G (M + m)} \ cdot a ^ 3$

onde:

T = objeto do período sideral
a = objeto do semi-eixo maior
G = constante gravitacional = 6,67 × 10 ^-11 N • m² / kg²
M = massa de um objeto
m = massa de outro objeto

Para objetos que orbitam o Sol, pode ser conveniente usar unidades de anos, AU, e massas solares, de modo que L, e os vários 4π² factores de conversão cancelar. Também com m << M, podemos definir m + M = M, por isso temos simplesmente 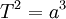$T ^ 2 = a ^ 3$ . Note-se que os valores de L e massas planetárias não são conhecidos com boa precisão; no entanto, os produtos geneticamente modificados (a atração Keplerian) são conhecidos por uma precisão extremamente elevada.

Definir ponto A para ser o periapsis, e ponto B como o apoapsis do planeta em órbita quando o sol.

A segunda lei de Kepler afirma que o corpo em órbita irá varrer áreas iguais em quantidades iguais de tempo. Se olharmos agora para um pequeno período de tempo nos momentos quando o planeta está nos pontos A e B, então podemos aproximar a área varrida para fora como um triângulo com uma altitude igual à distância entre o planeta eo Sol, e a base de igualdade para os tempos de tempo a velocidade do planeta.

$\ Begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot (1- \ epsilon) a \ cdot V_A \, dt = \ begin {matrix} \ frac {1} {2} \ end { matrix} \ cdot (1+ \ epsilon) a \ cdot V_B \, dt$

$(1- \ epsilon) \ cdot V_A = (1+ \ epsilon) \ cdot V_B$

$V_A = V_B \ cdot \ frac {1+ \ epsilon} {1- \ epsilon}$

Usando o lei da conservação de energia para a energia total do planeta nos pontos A e B,

$\ Frac {mV_A ^ 2} {2} - \ frac {} {GMM (1- \ epsilon) a} = \ frac {mV_B ^ 2} {2} - \ frac {} {GMM (1+ epsilon \) um }$

$\ Frac {V_A ^ 2} {2} - \ frac {V_B ^ 2} {2} = frac {GM} {(1- \ epsilon) a} \ - \ frac {GM} {(1 + epsilon \) um }$

$\ Frac {V_A ^ 2-V_B ^ 2} {2} = \ frac {GM} {a} \ cdot \ left (\ frac {1} {(1- \ epsilon)} - \ frac {1} {(1 + \ epsilon)} \ right)$

$\ Frac {\ left (V_B \ cdot \ frac {1+ \ epsilon} {1- \ epsilon} \ right) ^ 2-V_B ^ 2} {2} = \ frac {GM} {a} \ cdot \ left ( \ frac {1+ \ epsilon-1 + \ epsilon} {(1- \ epsilon) (1+ \ epsilon)} \ right)$

$V_B ^ 2 \ cdot \ left (\ frac {1+ \ epsilon} {1- \ epsilon} \ right) ^ 2-V_B ^ 2 = \ frac {2GM} {a} \ cdot \ left (\ frac {2 \ epsilon} {(1- \ epsilon) (1+ \ epsilon)} \ right)$

$V_B ^ 2 \ cdot \ left (\ frac {(1+ \ epsilon) ^ 2- (1- \ epsilon) ^ 2} {(1- \ epsilon) ^ 2} \ right) = \ frac {4GM \ epsilon} {A \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B ^ 2 \ cdot \ left (\ frac {1 + 2 \ epsilon + \ epsilon ^ 2-1 + 2 \ ï¿½silon- \ epsilon ^ 2} {(1- \ epsilon) ^ 2} \ right) = \ frac {4GM \ epsilon} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B ^ 2 \ cdot 4 \ epsilon = \ frac {4GM \ epsilon \ cdot (1- \ epsilon) ^ 2} {a \ cdot (1- \ epsilon) (1+ \ epsilon)}$

$V_B = \ sqrt {\ frac {GM \ cdot (1- \ epsilon)} {a \ cdot (1+ \ epsilon)}}.$

Agora que temos 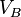$V_B$ , Podemos encontrar a taxa em que o planeta está varrendo a área em elipse. Esta taxa mantém-se constante, por isso, pode derivar-lo a partir de qualquer ponto que queremos, especificamente do ponto B.

$\ Frac {dA} {dt} = \ frac {\ frac {1} {2} \ cdot (1+ \ epsilon) a \ cdot V_B \, dt} {dt} = \ begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot (1+ \ epsilon) a \ cdot V_B$

$= \ Begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot (1+ \ epsilon) a \ cdot \ sqrt {\ frac {GM \ cdot (1- \ epsilon)} {a \ cdot (1+ \ epsilon)}} = \ begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot \ sqrt {GMa \ cdot (1- \ epsilon) (1+ \ epsilon)}$

No entanto, a área total da elipse é igual 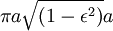$\ Pi a \ sqrt {(1- \ epsilon ^ 2)} uma$ . (Isso é o mesmo que 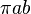$\ Pi a b$ , Porque 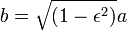$b = \ sqrt {(1- \ epsilon ^ 2)} uma$ ). O tempo que o planeta tirar para varrer toda a área da elipse é igual à área da elipse, de modo que,

$T \ cdot \ frac {dA} {dt} = \ pi a \ sqrt {(1- \ epsilon ^ 2)} uma$

$T \ cdot \ begin {matrix} \ frac {1} {2} \ end {matrix} \ cdot \ sqrt {GMa \ cdot (1- \ epsilon) (1+ \ epsilon)} = \ pi \ sqrt {(1 - \ epsilon ^ 2) ^ 2} um$

$T = \ frac {2 \ pi \ sqrt {(1- \ epsilon ^ 2)} a ^ 2} {\ sqrt {GMa \ cdot (1- \ epsilon) (1+ \ epsilon)}} = \ frac {2 \ pi a ^ 2} {\ sqrt {GMa}} = \ frac {2 \ pi} {\ sqrt {GM}} \ sqrt {a ^ 3}$

$T ^ 2 = \ frac {4 \ pi ^ 2} {GM} a ^ 3.$

No entanto, se a massa m não é negligenciável em relação a M, então o planeta orbita o sol com a mesma velocidade e posição exacta como um corpo muito pequeno em órbita um objecto de massa 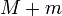$M + m$ (Veja massa reduzida). Para integrar o que, na fórmula acima, M deve ser substituído com 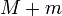$M + m$ , Para dar

$T ^ 2 = \ frac {4 \ pi ^ 2} {G (M + m)} a ^ 3.$

QED

Retirado de " http://en.wikipedia.org/w/index.php?title=Kepler%27s_laws_of_planetary_motion&oldid=198683410 "

We provide Linux to the World