Multiplicação

3 × 4 = 12, assim doze pontos podem ser dispostos em três filas de quatro (ou quatro colunas de três).

A multiplicação de números inteiros é a operação matemática da soma de múltiplas cópias do mesmo número. Por exemplo, quatro multiplicado por três é doze, uma vez que três conjuntos de quatro fazer doze:

Multiplicação também podem ser vistos como objectos de contagem dispostos numa retângulo, ou encontrar a área do retângulo cujos lados têm dado comprimentos.

Multiplicação é um dos quatro principais operações em aritmética elementar , ea maioria das pessoas aprender multiplicação básicos algoritmos em ensino fundamental. A inversa da multiplicação é divisão .

A multiplicação é generalizada a vários tipos de números e às construções mais abstratas, tais como matrizes.

Notação e terminologia

Multiplicação é escrito usando o sinal de multiplicação "x" entre os termos; isto é, em notação infix. O resultado é expresso com um sinal de igual. Por exemplo,

(Verbalmente, "duas vezes três é igual a seis")

Existem várias outras notações comuns para multiplicação:

• A multiplicação é por vezes designado por qualquer um meio ponto ou um período:

  

  O ponto médio é padrão no Estados Unidos , o Reino Unido e outros países onde o período é usado como um ponto decimal. Em alguns países que utilizam um vírgula como um ponto decimal, o período é utilizado para multiplicação em vez disso.
• O asterisco (por exemplo, 5 * 2) é usado frequentemente com computadores porque ele aparece em todos os teclados. Este uso se originou no Linguagem de programação Fortran.
• Em álgebra , multiplicação envolvendo variáveis muitas vezes é escrito como uma justaposição (por exemplo xy para tempos x y ou 5 x por cinco vezes x). Esta notação também pode ser usado para os números que estão rodeados por parênteses (por exemplo, 5 (2) ou (5) (2) por cinco vezes dois).

Os números devem ser multiplicadas são geralmente chamados de "fatores" ou "multiplicands". Ao pensar de multiplicação como a adição repetida, o número a ser repetida é chamado o "multiplicando", enquanto que o número de repetições é chamado o "multiplicador". Em álgebra, um número que é multiplicado por uma variável ou expressão (isto é, a 3 em 3 xy ²⁾ é chamado um coeficiente.

O resultado de uma multiplicação é chamado um produto, e é uma múltiplo de cada fator. Por exemplo 15 é o produto de 3 e 5, e é ao mesmo tempo um múltiplo de 3 e um múltiplo de 5.

Computação

Os métodos de referência para a multiplicação números usando lápis e papel necessitam de um tabela de multiplicação de produtos memorizadas ou consultadas de um pequeno número (normalmente dois números de 0 a 9), no entanto um método, o algoritmo de multiplicação camponês, não. Muitos currículos matemática desenvolvido de acordo com as normas do 1989 NCTM não ensinam métodos aritméticos padrão, em vez orientando os alunos a inventar seus próprios métodos de cálculo. Embora amplamente adotado por muitos distritos escolares em países como os Estados Unidos, eles têm encontrado resistência por parte de alguns pais e matemáticos, e alguns distritos, desde então, abandonado esses currículos em favor de matemática tradicional.

Multiplicando os números a mais do que um par de casas decimais à mão é tedioso e sujeito a erros. Logaritmos, foram inventados para simplificar esses cálculos. O régua de cálculo permitiu números a serem rapidamente multiplicado a cerca de três casas de precisão. Começando no início do século XX , mecânicos calculadoras , tais como a Marchant, multiplicação automatizada de até 10 números de um dígito. Electrónicos modernos computadores e calculadoras têm muito reduzida a necessidade de multiplicação com a mão.

Algoritmos históricos

Métodos de multiplicação foram documentados no Egito , Grécia , babilônico , Indus vale , e chineses civilizações.

Egípcios

O método egípcio de multiplicação de números inteiros e frações, documentado no Ahmes Papyrus, foi por sucessivas adições e duplicação. Por exemplo, para encontrar o produto de 13 e 21 um tinha para dobrar 21 de três vezes, obtendo 1 × 21 = 21, 2 × 21 = 42, 4 × 21 = 84, 8 × 21 = 168. O produto completo pode então ser encontrada somando os termos apropriados encontrados na sequência de duplicação:

13 × 21 = (1 + 4 + 8) x 21 = (1 × 21) + (4 x 21) + (8 x 21) = 21 + 84 + 168 = 273.

Babilônios

Os babilônios usaram um fração sexagesimal sistema de numeração posicional, análogo ao moderno sistema decimal. Assim, a multiplicação da Babilônia foi muito semelhante à multiplicação decimal moderna. Devido à relativa dificuldade de se lembrar de 60 × 60 produtos diferentes, os matemáticos babilônios empregado tabuada. Estas tabelas consistiu de uma lista dos primeiros vinte múltiplos de um certo número principais N: N, n 2, ..., 20 n; seguido pelos múltiplos de 10 N: 30 N 40 N e 50 N. Em seguida, para calcular qualquer produto sexagesimal, digamos 53 n, só necessário para adicionar 50 n 3 e n calculado a partir da tabela.

Chinês

Nos livros, Chou Pei Suan Ching com data anterior a 300 aC, ea Nove Capítulos da Arte Matemática, cálculos de multiplicação foram escritos em palavras, embora os primeiros matemáticos chineses empregou um ábaco em cálculos manuais que envolvem adição e multiplicação.

Indus Valley

Produto de 45 e 256. Nota a ordem dos números em 45 é revertida para baixo na coluna esquerda. O passo de transporte de multiplicação pode ser realizada na fase final do cálculo (em negrito), retornando o produto final de 45 × 256 = 11520.

Os matemáticos hindus iniciais da região do Vale do Indo usado uma variedade de truques intuitivas para realizar a multiplicação. A maioria dos cálculos foram realizados em pequenos comprimidos ardósia mão, usando tabelas de giz. Uma técnica que foi de multiplicação treliça (ou multiplicação gelosia). Aqui uma tabela foi elaborada com as linhas e colunas marcadas pelas multiplicands. Cada caixa da tabela foi dividido diagonalmente em dois, como um triangular Malha. As entradas da tabela mantidos os produtos parciais, escritos como números decimais. O produto pode, então, ser formada pela soma das diagonais para baixo da estrutura.

Método moderno

O método moderno de multiplicação baseada na Sistema numeral Hindu-Árabe foi primeiramente descrita por Brahmagupta. Brahmagupta deu regras para adição, subtração, multiplicação e divisão. Henry Burchard Fine, então professor de Matemática na Universidade de Princeton , escreveu o seguinte:

Os indianos são os inventores não só do próprio sistema decimal posicional, mas de a maioria dos processos envolvidos no cálculo elementar com o sistema. Adição e subtração eles realizaram muito como eles são realizados hoje em dia; multiplicação eles efectuada de muitas maneiras, nossos entre eles, mas eles fizeram divisão cumbrously.

Produtos de sequências

Notação pi Capital

O produto de uma seqüência de termos pode ser escrito com o símbolo do produto, que deriva da capital carta Π (Pi) no alfabeto grego . Posição Unicode U + 220F (Π) é definido um produto -ary n para este efeito, distinto de U + 03A0 (Π), a letra. Esta é definida como:

O índice dá o símbolo para um dummy ( 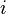no nosso caso) e o seu valor mais baixo ( 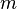); o sobrescrito dá o seu valor superior. Assim, por exemplo:

No caso de m = n, o valor do produto é a mesma que a do factor X _m. Se m> n, o produto é a produto vazio, com o valor 1.

Produtos infinitos

Pode-se também considerar os produtos de infinitamente muitos termos; estes são chamados produtos infinitos. Notationally, gostaríamos de substituir n acima pelo lemniscate (símbolo do infinito) ∞. Nos reais, o produto de uma tal série é definido como o limite do produto do primeiro 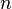termos, quanto 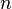cresce sem limites. Isto é, por definição,

Pode-se substituir de forma semelhante 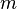com infinito negativo, e definir:

existem dois limites previstos.

Interpretação

Produto cartesiano

A definição de multiplicação como repetiu disso fornece uma maneira de chegar a uma interpretação set-teórica de multiplicação de números cardinais . Na expressão

se os n cópias de uma devem ser combinados em união disjunta então claramente eles devem ser feitas disjuntos; uma forma óbvia para fazer isto é a utilização de qualquer um ou n definida como a indexação para o outro. Em seguida, os membros do são exactamente as do Produto cartesiano . As propriedades da operação multiplicativo como sendo aplicável a números naturais siga trivialmente das propriedades correspondentes do produto cartesiano.

Propriedades

Para inteiros, frações, reais e números complexos, a multiplicação tem certas propriedades:

Propriedade comutativa

A ordem em que dois números são multiplicados não importa.

x · y = y · x.

Associatividade

Problemas envolvendo multiplicação unicamente são invariantes com respeito a ordem de operações.

(X · y) · · z = x (y · z).

Propriedade distributiva

Detém em relação à adição sobre a multiplicação. Essa identidade é de primordial importância na simplificação de expressões algébricas.

· x (y + z) = x + y · · x z.

Elemento de identidade

de multiplicação é 1; nada é multiplicado por um si. Isto é conhecido como a propriedade de identidade

· 1 x = x.

Zero elemento

Qualquer coisa multiplicada por zero é zero. Isto é conhecido como a propriedade zero da multiplicação.

X · 0 = 0

Propriedade Inverse

Cada número x, com excepção do zero, tem um multiplicativo inverso, 1 / x, tais que x · (1 / x) = 1.

Preservação da ordem

Multiplicação por um número positivo preserva ordem: se a> 0, em seguida, se b> c, em seguida, a · b> a · c. Multiplicação por um número negativo inverte ordem: se a <0, em seguida, se b> c, em seguida, a · b <a · c.

• Negativo vezes um qualquer número é igual ao negativo da esse número.

(-1) · X = (- X)

• Negativo um vezes um negativo é um positivo.

(-1) · (-1) = 1

Outros sistemas matemáticos que incluem uma operação de multiplicação pode não ter todas essas propriedades. Por exemplo, a multiplicação não, em geral, para as matrizes e conmutativo é quaternions.

Provas

Nem todas estas propriedades são independentes; alguns são uma consequência dos outros. Uma propriedade que pode ser comprovada dos outros é a propriedade zero da multiplicação. Está provado por meio do propriedade distributiva. Assumimos todas as propriedades usuais de adição e subtração, e - x significa o mesmo que

.

· x 0

= (X · 0) + x - x

= (X · 0) + (1 x ·) - X

= X · (0 + 1) - x

= (X · 1) - x

= X - x

= 0.

Então, temos provado:

X · 0 = 0.

A identidade (-1) · x = (- x) também pode ser provado usando a propriedade distributiva:

(-1) · X

= (-1) · X + x - x

= (-1) · X + 1 · x - x

= (-1 + 1) · x - x

= 0 · x - x

= 0 - x

= - X

A prova de que (-1) · (-1) = 1 agora é fácil:

(-1) · (-1)

= - (- 1)

= 1.

Multiplicação com axiomas de Peano

No livro Arithmetices principia, nova methodo exposita, Giuseppe Peano propôs um novo sistema para a multiplicação baseada em seus axiomas para números naturais.

• um × 1 = um
• um × b '= (a × b) + a

Aqui, b 'representa o sucessor de b, ou o número natural que segue b. Com a outra nove axiomas, é possível provar regras comuns de multiplicação, tais como as propriedades distributivas ou associativas.

Multiplicação com a teoria dos conjuntos

É possível, embora difícil, para criar uma definição recursiva de multiplicação com a teoria dos conjuntos. Um sistema deste tipo geralmente baseia-se na definição de Peano multiplicação.

Multiplicação em teoria dos grupos

É fácil mostrar que há um grupo de multiplication- os números racionais não-zero. A multiplicação com números diferentes de zero satisfaz

• Encerramento - Para todos a e b no grupo, um × b é no grupo.
• Associatividade - Esta é apenas a associatividade: (a × b) x c = a × (b × c)
• Identity - Isto segue em linha reta a partir da definição de Peano. Qualquer coisa é multiplicado por um si.
• Inverse - Todos os números não-zero têm um multiplicativo inverso.

A multiplicação é também um grupo abeliano, uma vez que segue a propriedade comutativa.

a × b = b um ×

Multiplicação de diferentes tipos de números

Os números podem contar (3 maçãs), ordem (o terceiro de maçã), ou medida (3,5 pés de altura); como a história da matemática progrediu de contar com os dedos à mecânica modelagem quantuum, multiplicação foi generalizado para tipos mais complicados e abstratos de números, e coisas que não são números (como matrizes ) ou não se parecem muito parecido números (tal como quaternions).

• Inteiros N × M é a soma de m cópias de N, quando n e m são números inteiros positivos. Isto dá o número de coisas em uma matriz N ampla e M elevado. Generalização para números negativos pode ser feito por (N × -M) = - (N × H).

• Racionais Generalização a frações A / B × C / D é através da multiplicação dos numeradores e denominadores respectivamente: A / B × C / D = (A x B) / (C × D). Isto dá a área de um rectângulo A / B alta e C / D de largura, e é o mesmo que o número de coisas em uma matriz quando os números racionais acontecem ser números inteiros.

• Reais X x Y é o limite dos produtos dos termos correspondentes em certas sequências de racionais que convergem para x e y, respectivamente, e é significativo no cálculo . Isto dá a área de um rectângulo de largura x altura e y. Veja acima .

• Complexo Considerando números complexos Z1 e Z2 como pares ordenados ou números reais (a1, b1) e (a2, b2), o produto z1 z2 é × (a1 × a2 - b2 b1 ×, × a1 + a2 b2 b1 ×). Este é o mesmo que para reais, a1 a2 ×, quando as partes imaginárias B1 e B2 são iguais a zero.

• Mais generalizações Veja acima e Multiplicativo Group, que inclui, por exemplo, a multiplicação de matrizes. Um, conceito muito geral e abstrata de multiplicação é como o (segundo) operação binária "multiplicatively denotado" em um anel. Um exemplo de um anel que não é qualquer um dos sistemas de numeração acima é anéis de polinômios (você pode somar e multiplicar polinômios, mas polinômios não são números em qualquer sentido usual.)

• Divisão Frequentemente divisão x / y é o mesmo que a multiplicação por uma inversa, x x (1 / y). Multiplicação para alguns tipos de "números" pode ter divisão correspondente, sem inversas; numa Integral de domínio x pode não ter inversa "1 / x", mas x / y pode ser definida. Em um Anel Divisão existem inversas, mas eles não são conmutativo (desde 1 / x x 1 / y não é o mesmo que 1 / y X 1 / x, x / y pode ser ambígua).