A teoria do grupo

Em álgebra abstrata , a teoria do grupo estuda as estruturas algébricas conhecidos como grupos . Um grupo é um definir G (o conjunto subjacente) fechado sob um binário operação satisfazer três axiomas:

1. A operação é associativa .
2. A operação tem um elemento de identidade.
3. Cada elemento tem uma elemento inverso.

(Leia sobre para definições mais precisas.)

Grupos são blocos de construção mais elaboradas estruturas algébricas tais como anéis, campos e espaços vetoriais , e se repetem em toda a matemática. A teoria do grupo tem muitas aplicações na física e química , e é potencialmente aplicável em qualquer situação caracterizada pela simetria .

A ordem de um grupo, é a cardinalidade de G; grupos podem ser de ou finito ordem infinita. O classificação dos grupos finitos simples é uma grande conquista matemática do século 20.

Conceitos de teoria de grupo

Para os não-matemáticos

Um grupo consiste de uma coleção de objetos abstratos ou símbolos, e uma regra para combiná-los. A regra combinação indica como esses objetos devem ser manipulados. Daí grupos são uma forma de fazer a matemática com símbolos em vez de números concretos.

Mais precisamente, pode-se falar de um grupo sempre que um definir, em conjunto com um operação que sempre combina dois elementos deste conjunto, por exemplo, um x b, sempre cumpre os seguintes requisitos:

1. A combinação de dois elementos do conjunto produz um elemento do mesmo conjunto ( fecho);
2. O bracketing não é importante ( associatividade ): a × (b × c) = (a × b) × c;
3. Há um elemento que não causa qualquer coisa acontecer ( elemento de identidade): a × 1 = 1 × a = a;
4. Cada elemento tem uma "imagem espelho" ( elemento inversa) 1 / um que tem a propriedade de produzir o elemento de identidade quando combinado com um: um × 1 / A = 1 / A X = um 1

Caso especial: Se a ordem dos operandos não afeta o resultado, isto é, se a × b = b × detém um ( comutatividade ), então falamos de uma grupo abeliano.

Alguns exemplos numéricos simples de grupos abelianos são:

• Inteiros com a operação de adição "+" como operação binária e zero como elemento de identidade
• Números racionais sem zero, com a multiplicação "x" como operação binária eo número um como elemento de identidade. Zero tem que ser excluída, porque não tem um elemento inversa. ("1/0" é indefinido.)

Essa definição de grupos é deliberadamente muito geral. Ele permite tratar como grupos não apenas conjuntos de números com operações correspondente, mas também outros objectos e símbolos abstratos que preenchem as propriedades necessárias, tais como polígonos com suas rotações e reflexões em grupos diedro.

James Newman resumiu a teoria do grupo da seguinte forma:

Definição de um grupo

Um grupo (G *) é um definir G fechado sob uma operação binária * satisfaça a seguinte 3 axiomas:

• Associativity : Para tudo a, b e c em L, (a * b) * c = a * (b * c).
• Elemento de identidade: Não existe um e ∈ G tal que para todo um em G, e * a = a * e = a.
• Elemento Inverso: Para cada um em G, existe um elemento b em G tal que a * b * b = A = E, onde E é o elemento de identidade.

Na terminologia álgebra universal, um grupo é um variedade, e de um álgebra de tipo .

Subgrupos

Um conjunto H é um subgrupo de um grupo G, se for um subconjunto de G e é um grupo com a operação definida em G. Em outras palavras, H é um subgrupo de (L, *) se a restrição de * H é para um grupo de operação em H.

Um sub-grupo H é um subgrupo normal de G se para todos H em H e em g G, GHG ^-1 também é em H. Uma alternativa (mas equivalente) definição é que um subgrupo é normal se a sua esquerda e direita cosets coincidem. Subgrupos normais desempenham um papel distinto em virtude do facto de a recolha de classes laterais de um N subgrupo normal num grupo G naturalmente herda um grupo de estrutura, permitindo a formação de a grupo quociente, geralmente denotado G / N (também chamado às vezes um fator grupo).

As operações envolvendo grupos

A homomorphism é um mapa entre dois grupos que preserva a estrutura imposta pelo operador. Se o mapa é bijective, então é um isomorfismo. Um isomorfismo de um grupo de si é um automorphism. O conjunto de todos os automorfismos de um grupo é um grupo chamado o grupo automorphism. O núcleo de uma homomorphism é um subgrupo normal do grupo.

A a ação do grupo é um mapa que envolve um grupo e um conjunto, onde cada elemento no grupo define um mapa bijective em um conjunto. Acções de grupo são usadas para comprovar a Sylow teoremas e para provar que o um centro de p-grupo não é trivial.

Tipos especiais de grupos

Um grupo é:

• Abeliano (ou conmutativo ), se comuta seus produtos (isto é, para todo a, b em L, a * b = b * a). Um grupo não-abeliano é um grupo que não é abeliano. O termo "abelian" homenageia o matemático Niels Abel.

• Cíclico se for gerado por um único elemento.

• Simples se não tiver subgrupos normais não triviais.

• Solvable (ou solúvel), se tiver uma série normal cujo grupos quociente são todos abelian. O facto de que o S _5, o grupo simétrico em cinco elementos, não é solúvel é usado para provar que alguns polinómios quinto grau não pode ser resolvida por radicais.

• Livre se existe um subconjunto de G, H, de modo a que todos os elementos de G pode ser escrita de forma única como produtos (ou cordas) de elementos de H. Cada grupo é o homomorphic imagem de algum grupo livre.

Alguns teoremas úteis

Alguns resultados básicos na teoria do grupo elementar :

• O teorema de Lagrange: se G é um grupo finito e H é um subgrupo de G, então a ordem (isto é, o número de elementos) de H divide a ordem de L.
• Teorema de Cayley: cada grupo G é isomórfico a um subgrupo da grupo simétrico em G.
• Sylow teoremas: se p ⁿ (e p prime) é o maior poder de p dividindo a ordem de um grupo finito G, então existe um subgrupo de ordem p ^n. Este é talvez o resultado básico mais útil em grupos finitos.
• O Borboleta lema é um resultado técnico no estrutura de subgrupos de um grupo.
• O Teorema fundamental sobre homomorfismos relaciona a estrutura de dois objetos entre os quais um homomorfismo é dado, e do kernel e imagem do homomorphism.
• Jordan-Hölder teorema: qualquer série dois composição de um determinado grupo são equivalentes.
• Krull-Schmidt teorema: um grupo G que satisfaçam determinadas condições finitude para cadeias dos seus subgrupos, pode ser escrito exclusivamente como um produto finito direta de subgrupos indecomponíveis.
• Lema de Burnside: o número de órbitas de um ação do grupo de um conjunto é igual ao número médio de pontos fixos de cada elemento do grupo.

Conexão de grupos e simetria

Dado um objeto estruturado de qualquer espécie, a simetria é um mapeamento do objeto em si, que preserva a estrutura. Por exemplo, as rotações de uma esfera são simetrias da esfera. Se o objeto é um conjunto com nenhuma estrutura adicional, uma simetria é um mapa bijective a partir do conjunto de si mesmo. Se o objecto é um conjunto de pontos no plano, com a sua estrutura métrica, uma simetria é um bijection do conjunto para que preserva-se a distância entre cada par de pontos (um isometria).

Os axiomas de um grupo de formalizar os aspectos essenciais da simetria .

1. Encerramento da lei grupo - Isto diz que se você tomar uma simetria de um objeto, e em seguida, aplicar uma outra simetria, o resultado ainda será uma simetria.
2. A existência de uma identidade - Isto quer dizer que o objecto fixo mantendo sempre uma simetria de um objecto.
3. A existência de inversas - Este diz que cada simetria pode ser desfeita.
4. Associatividade - Desde simetrias são funções em um espaço e composição de funções são associativo, este axioma é necessário para fazer um grupo formal de se comportar como funções.

O teorema de Frucht diz que cada grupo é o grupo de simetria de alguns grafo. Assim, cada grupo abstrato é realmente as simetrias de um objeto explícito.

Aplicações de teoria de grupos

Algumas aplicações importantes da teoria do grupo incluem:

• Os grupos são muitas vezes usadas para captar a simetria interna de outras estruturas. Uma simetria interna de uma estrutura é geralmente associada com um propriedade invariante; o conjunto de transformações que preservar esta propriedade invariante, em conjunto com a operação de composição de transformações, formam um grupo chamado de grupo de simetria. Veja também automorphism grupo.

• Galois teoria , que é a origem histórica do conceito de grupo, usa grupos para descrever as simetrias das raízes de um polinômio (ou mais precisamente os automorfismos de álgebras geradas por essas raízes). Os grupos solúveis são assim chamado por causa de seu papel proeminente nessa teoria. Teoria de Galois foi originalmente usado para provar que polinômios do quinto grau e superior não pode, em geral, ser resolvidos de forma fechada por radicais, a forma como polinômios de menor grau pode.

• Grupos abelianos, que adicionam a propriedade comutativa a * b = b *, um subjacentes várias outras estruturas em álgebra abstrata, como anéis, campos e módulos.

• Em topologia algébrica, os grupos são usados para descrever as invariantes de espaços topológicos. Eles são chamados de "invariantes" porque são definidos de tal modo que eles não se alterar o espaço é sujeito a alguma deformação. Os exemplos incluem o grupo fundamental, grupos de homologia e grupos de cohomologia. O nome do subgrupo de torção de um grupo infinito mostra o legado de topologia na teoria do grupo.

• O conceito do Grupo de Lie (nomeado após matemático Sophus Lie) é importante no estudo de equações diferenciais e colectores ; eles descrevem as simetrias de estruturas geométricas e analíticas contínuas. Análise sobre estes e outros grupos é chamada análise harmônica.

• Na análise combinatória , a noção de permutação grupo eo conceito de ação do grupo são muitas vezes utilizados para simplificar a contagem de um conjunto de objetos; ver, nomeadamente, Lema de Burnside.

• Uma compreensão da teoria do grupo também é importante em física e química e ciência dos materiais. Na física, os grupos são importantes porque descrevem as simetrias que as leis da física parecem obedecer. Os físicos estão muito interessados em representações do grupo, especialmente de Grupos de Lie, uma vez que essas representações muitas vezes apontam o caminho para as "possíveis" teorias físicas. Exemplos do uso de grupos em física incluem: Modelo Padrão , Teoria de gauge, Grupo de Lorentz, Grupo de Poincaré

• Em química , os grupos são usados para classificar estruturas cristalinas, poliedros regulares, e o simetrias das moléculas. Os grupos de pontos atribuídos podem então ser utilizados para determinar as propriedades físicas (tais como e polaridade quiralidade), propriedades espectroscópicas (particularmente úteis para Espectroscopia Raman e Espectroscopia de infravermelho), e para a construção de orbitais moleculares.

• A teoria do grupo é usado extensivamente na criptografia de chave pública. Em Elliptic Curve Cryptography-, muito grandes grupos de primeira ordem são construídos através da definição de curvas elípticas sobre campos finitos.

História

Existem três raízes históricas da teoria do grupo: a teoria da equações algébricas, teoria dos números e geometria . Euler , Gauss , Lagrange , Abel e matemático francês Galois foram os primeiros pesquisadores no campo da teoria do grupo. Galois é homenageado como a teoria do grupo primeiro matemático vinculação e teoria de campo, com a teoria de que agora é chamado de teoria de Galois .

Uma fonte precoce ocorre no problema da formação de uma 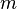equação th grau tendo como suas raízes m das raízes de uma dada 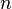equação th-grau ( ). Para casos simples, o problema remonta a Hudde (1659). Saunderson (1740) observou que a determinação dos fatores quadráticos de uma expressão biquadrática conduz necessariamente a uma equação sêxtica, e Le Sœur (1748) e Waring (1762-1782) ainda aprofundou a idéia.

Uma base comum para a teoria de equações com base na do grupo de permutações foi encontrado pelo matemático Lagrange (1770, 1771), e sobre este foi construído a teoria de substituições. Ele descobriu que as raízes de todos os resolventes (résolvantes, réduites) que ele examinadas são funções racionais das raízes das respectivas equações. Para estudar as propriedades dessas funções, ele inventou um Calcul des Combinaisons. O trabalho contemporâneo de Vandermonde (1770) também antecipou a teoria que vem.

Ruffini (1799) tentou uma prova da impossibilidade de resolver o quintic e equações mais elevados. Ruffini distinguido o que agora são chamados de intransitivo e transitivo, e imprimitive e grupos de primitivas, e (1801) utiliza o grupo de uma equação sob o nome l'assieme delle permutazioni. Ele também publicou uma carta do Abbati para si mesmo, em que o grupo idéia é proeminente.

Galois descobriu que se são o 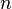raízes de uma equação, há sempre um grupo de permutações do 'S de tal modo que (1) todas as funções das raízes por invariáveis as substituições do grupo é racionalmente conhecido, e (2), pelo contrário, todas as funções racionalmente determinável das raízes é invariante sob as substituições do grupo. Galois também contribuiu para a teoria da equações modulares e para a de funções elípticas. Sua primeira publicação sobre a teoria do grupo foi feita com a idade de dezoito anos (1829), mas suas contribuições atraiu pouca atenção até que a publicação de seus artigos recolhidos em 1846 (Liouville, Vol. XI).

Arthur Cayley e Augustin Louis Cauchy estavam entre os primeiros a apreciar a importância da teoria, e este último são especialmente devido uma série de teoremas importantes. O assunto foi popularizada por Serret, que dedicou seção IV do seu álgebra com a teoria; por Camille Jordan, cuja Traité des Substituições é um clássico; e para Eugen Netto (1882), cuja teoria de substituições e suas aplicações para a álgebra foi traduzido para o Inglês por Cole (1892). Outros teóricos do grupo do século XIX eram Bertrand, Charles Hermite, Frobenius, Leopold Kronecker, e Emile Mathieu.

Walther von Dyck foi o primeiro (em 1882) para definir um grupo, no sentido abstrato cheio de esta entrada.

O estudo do que agora são chamados Deite grupos, e sua subgrupos discretas, como grupos de transformação, começou sistematicamente em 1884 com Sophus Lie; seguido de trabalho de Matar, Estudo, Schur, Maurer, e Cartan. O descontínua ( grupo discreto) teoria foi construída por Felix Klein, Lie, Poincaré, e Charles Émile Picard, em conexão, nomeadamente, com formas modulares e monodromia.

O classificação dos grupos finitos simples é um vasto corpo de trabalho a partir de meados do século 20, classificando toda a finito grupos simples.

Outros contribuintes importantes para a teoria do grupo incluem Emil Artin, Emmy Noether , Sylow, e muitos outros.

Alfred Tarski provou a teoria do grupo elementar indecidível.

Miscelânea

Uma aplicação da teoria do grupo é teoria dos conjuntos musical.

Em filosofia , Ernst Cassirer teoria de grupos relacionados com a teoria da percepção de Psicologia da Gestalt. Ele tomou a Constância perceptiva de que psicologia como análoga à invariantes de teoria de grupos.