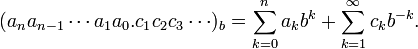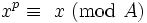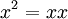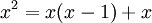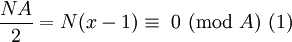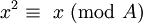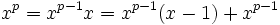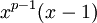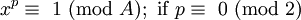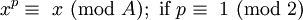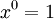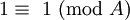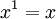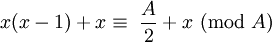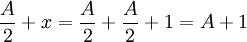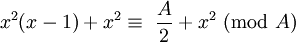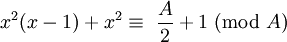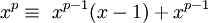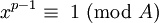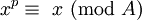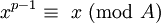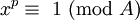Sistema de numeração
Informações de fundo
Este conteúdo da Wikipedia foi escolhida pela SOS Children para adequação nas escolas de todo o mundo. Crianças SOS é a maior doação de caridade do mundo órfãos e crianças abandonadas a chance da vida familiar.
| Sistemas numerais por cultura |
|---|
|
| Sistemas de posicionamento por base |
| Decimal (10) |
| Ternário equilibrada |
| Lista de sistemas numerais |
Um sistema de numeração (ou sistema de numeração) é um notação matemática para representar números de um dado conjunto de símbolos de uma forma consistente. Pode ser visto como o contexto que permite que o número "11" para ser interpretado como o binário numeral de três, o decimal numeral de onze, ou outros números em diferentes bases.
Idealmente, um sistema de numeração irá:
- Representam um conjunto útil de números (por exemplo, todos números inteiros, inteiros ou números reais )
- Dê a cada número representou uma representação única (ou pelo menos uma representação padrão)
- Refletir a estrutura algébrica e aritmética dos números.
Por exemplo, o habitual decimal representação de números inteiros dá a cada número inteiro uma representação única como um finito seqüência de dígitos , com as operações da aritmética (adição, subtração, multiplicação e divisão) estando presente como padrão algoritmos da aritmética. No entanto, quando a representação decimal é usado para os racionais ou reais números, a representação já não é único: muitos números racionais tem dois números, um padrão que termina, tal como 2,31, e outro que repete, como 2,309999999 .... Numerais que terminam não tem dígitos diferentes de zero depois de uma dada posição. Por exemplo, números semelhantes 2,31 e 2,310 são tomadas para ser o mesmo, exceto nas ciências experimentais, onde uma maior precisão é denotada pelo zero à direita.
Sistemas numerais são chamados às vezes sistemas de número , mas esse nome é enganador, como poderia referir-se a diferentes sistemas de números, tais como o sistema de números reais , o sistema de números complexos , o sistema de p números -adic, etc. Tais sistemas não são o tema deste artigo.
Tipos de sistemas numerais
A mais utilizada sistema de numerais como é conhecido Algarismos hindu-arábicos, e dois grandes matemáticos indianos poderiam ser dado o crédito para desenvolvê-los. Aryabhatta de Kusumapura que viveu durante o século 5 desenvolveram o valor lugar notação e Brahmagupta um século mais tarde introduziu o símbolo zero.
O sistema de numeração é o mais simples sistema de numeração unária, em que cada número natural é representado por um número correspondente de símbolos. Se o símbolo / é escolhido, por exemplo, então o número de sete seria representada pelo ///////. Marcas de registro representam um tal sistema ainda em uso comum. Na prática, o sistema unária é normalmente útil apenas para um pequeno número, embora desempenhe um papel importante na ciência da computação teórica. Além disso, Elias codificação gamma que é comumente usado em compressão de dados expressa números de tamanho arbitrário usando unary para indicar o comprimento de um numeral binário.
A notação unary pode ser abreviado com a introdução de símbolos diferentes para determinados valores novos. Muito comumente, esses valores são potências de 10; assim, por exemplo, se / representa um, - por dez e + 100 para, em seguida, o número 304 pode ser representado como compactamente +++ //// e número 123 como + - - /// sem qualquer necessidade de zero. Isto é chamado registe-valor notação. A antiga Sistema egípcio é desse tipo, eo sistema romano é uma modificação desta idéia.
Mais ainda úteis são os sistemas que empregam as abreviaturas especiais para repetições de símbolos; por exemplo, usando as primeiras nove letras do nosso alfabeto para essas abreviaturas, com uma posição de "uma ocorrência", B "duas ocorrências", e assim por diante, podemos então escrever C + D / para o número 304. O sistema numeral de Inglês é desse tipo ("trezentos [e] quatro"), como são as de praticamente todos os outros faladas línguas , independentemente do que os sistemas de escrita que eles adotaram.
Mais elegante é um sistema posicional, também conhecido como notação de valor local. Novamente trabalho na base 10, usamos diferentes dez dígitos 0, ..., 9 e usar a posição de um dígito para significar a potência de dez dígitos é a que deve ser multiplicada com, como em 304 = 3 × 100 + 0 × 10 + 4 × 1. Note-se que de zero , o que não é necessário em outros sistemas, é de importância crucial aqui, a fim de ser capaz de "saltar" uma potência. O Sistema de numeração hindu-arábico, emprestado da Índia , é um sistema de base 10 posicional; ela é usada hoje em dia por todo o mundo.
A aritmética é muito mais fácil em sistemas posicionais do que nos aditivos anteriores; Além disso, sistemas de aditivos têm uma necessidade de um número potencialmente infinita de símbolos diferentes para as diferentes potências de 10; sistemas posicionais precisa apenas 10 símbolos diferentes (assumindo que ele usa base 10).
Os números utilizados ao escrever números com dígitos ou símbolos podem ser divididos em dois tipos que podem ser chamados a números aritméticos 0,1,2,3,4,5,6,7,8,9 e o numerais geométricas 1,10,100,1000,10000 ..., respectivamente. Os sistemas de valor sinal utilizar apenas os números geométricas eo sistema posicional utilizar apenas os números aritméticos. O sistema de sinal de valor não necessita de números aritméticos porque eles são feitos pela repetição (excepto para o O sistema Ionic), eo sistema de posicionamento não precisa de números geométricos porque eles são feitos por posição. No entanto, a língua falada usa tanto aritmética e números geométricos.
Em certas áreas da ciência da computação, um sistema posicional k base- modificado é usado, chamado numeração bijective, com algarismos 1, 2, ..., k (k ≥ 1) e zero sendo representado por uma string vazia. Isto estabelece um bijection entre o conjunto de todas as strings de dígitos eo conjunto de inteiros não negativos, evitando a não-singularidade causada por zeros à esquerda. Bijective base- k numeração também é chamado notação -adic k, não deve ser confundida com números p-adic. Bijective base-1 o mesmo que unário.
As bases utilizadas
Em computação
Interruptores, imitada por seus sucessores eletrônicos construído originalmente de tubos de vácuo e da tecnologia moderna de transistores, têm apenas dois estados possíveis: "aberto" e "fechado". Substituindo aberto e fechado = 1 = 0 (ou o contrário) produz todo o conjunto de dígitos binários. Este sistema de base 2 ( binário ) é a base para computadores digitais. É usado para realizar aritmética inteira em quase todos os computadores digitais; alguns exóticos base-3 ( ternários) e base-10 computadores também foram construídas, mas esses projetos foram descartados no início da história da computação hardware .
Modernos computadores usar transistores que representam dois estados com tensões de alta ou baixa. A menor unidade de memória para este estado binário é chamado um pouco. Os bits estão dispostas em grupos para ajudar no processamento, e para tornar os números binários mais curto e mais viável para os seres humanos. Mais recentemente, estes grupos de bits, tal como bytes e as palavras, são dimensionados em múltiplos de quatro. Assim base 16 ( hexadecimal ) é comumente usado como taquigrafia. Base de dados de 8 (octal) também tem sido utilizada para o efeito.
Um computador não trata todos os seus dados como numérico. Por exemplo, algumas das quais podem ser tratados como dados ou instruções de programa, tais como texto. No entanto, aritmética e lógica booleana constituem operações mais internos. Números inteiros são representados exatamente, como inteiros. Os números reais , permitindo que valores fracionários, são geralmente aproximada como números de ponto flutuante. O computador utiliza métodos diferentes para fazer aritmética com estes dois tipos de números.
Cinco
Um sistema de base-5 ( quinário) tem sido usado em muitas culturas para a contagem. É evidente que se baseia no número de dedos em uma mão humana. Pode também ser considerado como uma sub-base de outras bases, como a base 10 e a base 60.
Oito
Um sistema de base-8 ( octal) foi concebido pela Yuki do norte da Califórnia, que usou os espaços entre os dedos para contar. Zero a sete são os únicos dígitos possíveis. Há também evidência lingüística que sugere que a Idade do Bronze Proto-Indo europeus (dos quais a maioria das línguas europeias e índicos descem) poderia ter substituído um sistema de base 8 (ou um sistema que só podia contar até 8) com um sistema de base 10. A prova é que a palavra para 9, NEWM, é sugerida por alguns como derivar da palavra para 'novo', newo-, sugerindo que o número 9 tinha sido recentemente inventado e chamado de "novo número" (Mallory & Adams 1997) .
Dez
O sistema de base 10 ( decimal ) é o mais comumente usado hoje. Supõe-se para ter originado porque os seres humanos têm dez dedos. Estes sistemas utilizam frequentemente uma base sobreposta maior. Ver Superbase Decimal.
Doze
Base-12 sistemas ( duodecimal ou dozenal) têm sido muito populares, porque a multiplicação ea divisão são mais fáceis do que na base-10, com adição e subtração sendo tão fácil. 12 é uma base útil porque tem muitos factores . É a menor múltiplo de um a quatro e de seis. Há ainda uma palavra especial para "dúzia" e, assim como há uma palavra para 10 2, cem, há também uma palavra para 12 2, bruto. Base-12 poderia ter originado a partir do número de juntas nas quatro dedos de uma mão, excluindo o polegar, o qual é utilizado como um indicador na contagem.
Doze é uma unidade britânica de medida comum. Há doze polegadas a um pé. Antes de 1971, em moeda britânica, havia 12 centavos a um xelim. . Inglês palavras para números também são "base-12 'em que não há uma única palavra para os números de um a doze anos, com" treze "ser a primeira palavra que foi formado pela combinação de números (três e dez).
Há 24 horas por dia, normalmente contados até 12 (até meio-dia pm) e mais uma vez até a meia-noite ( am), muitas vezes divididos por seis horas na contagem (por exemplo, na Tailândia ) ou como alterna entre o uso de termos como 'noite', 'manhã', 'tarde', e 'noite', enquanto outros idiomas usar tais termos com durações de 3 a 9 horas, muitas vezes de acordo com interruptores em algumas das três horas marcas do intervalo.
Múltiplos de 12 já estão em uso comum como unidades inglesas de resolução no mundo analógico e impressão digital, onde 1 ponto equivale a 1/72 de polegada e 12 pontos igual a 1 pica, e impressora resoluções como 360, 600, 720, 1200 ou 1440 dpi (pontos por polegada) são comuns. Trata-se de combinações de base-12 e base 10 factores: (3 × 12) × 10, 12 × (5 × 10), (6 x 12) x 10, 12 x (10 x 10) e (12 × 12) × 10.
Vinte
A civilização maia e de outras civilizações Pre-Columbian Mesoamérica usadas base-20 ( vigesimal), possivelmente proveniente do número de dedos e dedos do pé de uma pessoa. Evidência de sistemas de contagem de base 20 também é encontrado nas línguas da região central e ocidental de África .
Possíveis restos de um sistema de base-20 também existe em francês, como visto nos nomes dos números de 60 a 99. Por exemplo, sessenta e cinco é soixante-cinq (literalmente, "sessenta [e] cinco"), enquanto setenta -Cinco é soixante-quinze (literalmente, "sessenta [e] quinze"). Além disso, para qualquer número entre 80 e 99, o "dezenas-coluna" número é expressa como um múltiplo de vinte (um pouco semelhante à forma Inglês arcaico de fala de " scores "). Por exemplo, oitenta e dois é quatre-vingt-deux (literalmente, quatro vinte [s] [e] dois), enquanto noventa e dois quatre-vingt é-douze (literalmente, quatro vinte [s] [e ] doze).
O Língua irlandesa também usou base-20 no passado, vinte ser fichid, quarenta DHA fhichid, fhichid sessenta e oitenta trí fhichid ceithre. Um remanescente desse sistema pode ser visto na palavra moderna para 40, daoichead.
Numerais dinamarqueses exibir uma base-20 estrutura semelhante.
Sessenta
Base de dados de 60 ( sexagesimal) foi usada pelos sumérios e seus sucessores na Mesopotâmia e sobrevive até hoje em nosso sistema de tempo (daí a divisão de uma hora para 60 minutos e um minuto para 60 segundos) e em nosso sistema de medida angular (um grau é dividido em 60 minutos e um minuto é dividido em 60 segundos). 60 também tem um grande número de fatores, incluindo os seis primeiros números de contagem . Base-60 sistemas são acreditados para ter originado através da fusão de base-10 e base-12 sistemas. O Calendário chinês, por exemplo, usa uma base 60 Jia-Zi 甲子 sistema para denotar anos, a cada ano dentro do ciclo de 60 anos de ser nomeado com dois símbolos, o primeiro ser base-10 (chamado Tian-Gan 天干 ou troncos celestes) eo segundo símbolo sendo base 12 (chamado Di-Zhi 地支 ou ramos terrestres). Ambos os símbolos são incrementados em anos sucessivos, até que o primeiro padrão se repete 60 anos depois. O segundo símbolo de este sistema também está relacionado com o de 12 animais Sistema do zodíaco chinês. O sistema Jia-zi também pode ser aplicado a contagem de dias, com um ano contendo cerca de seis ciclos de 60 dias.
De base dupla (vinte e cinco)
Muitos sistemas de contagem antigos utilizar 5 como base primária, quase certamente vindo do número de dedos na mão de uma pessoa. Muitas vezes, estes sistemas são complementados com uma base secundária, às vezes dez, vinte vezes. Em alguns Línguas africanas a palavra para 5 é o mesmo que "mão" ou "punho" ( Dyola linguagem da Guiné-Bissau , Banda linguagem da África Central). Contar continua através da adição de 1, 2, 3, 4 ou a combinações de 5, até que a base secundária é atingido. No caso de vinte anos, esta palavra muitas vezes significa "homem completo". Este sistema é referido como quinquavigesimal. Pode ser encontrada em muitas línguas do Sudão região.
Nomes de base
1 - unary 2 - binário 3 - ternário / ternária 4 - quaternário 5 - quinary / quinternary 6 - senário / heximal / hexary 7 - septenary / septuary 8 - octal / octonária / octonal / octimal 9 - grupo de nove / novary / noval 10 - decimal / denary 11 - undecimal / undenary / unodecimal 12 - dozenal / duodecimal / duodenário 13 - tridecimal / tredecimal / triodecimal 14 - tetradecimal / quadrodecimal / quattuordecimal 15 - pentadecimal / quindecimal 16 - hexadecimal / sexadecimal / sedecimal 17 - septendecimal / heptadecimal 18 - octodecimal / decennoctal 19 - nonadecimal / novodecimal / decennoval 20 - vigesimal / bigesimal / bidecimal 21 - unovigesimal / unobigesimal 22 - duovigesimal 23 - triovigesimal 24 - quadrovigesimal / quadriovigesimal 26 - hexavigesimal / sexavigesimal 27 - heptovigesimal 28 - octovigesimal 29 - novovigesimal 30 - trigesimal / triogesimal 31 - unotrigesimal (... repetição padrão de nomenclatura ...) 36 - hexatridecimal / sexatrigesimal (... repetição de nomeação padrão ...) 40 - quadragesimal / quadrigesimal 41 - unoquadragesimal (... repetição de nomeação padrão ...) 50 - quinquagesimal / pentagesimal 51 - unoquinquagesimal (... repetição padrão de nomenclatura .. .) 60 - sexagesimal (... repetição de nomeação padrão ...) 64 - quadrosexagesimal (... repetição padrão de nomenclatura ...) 70 - septagesimal / heptagesimal 80 - octagesimal / octogesimal 90 - nonagesimal / novagesimal 100 - centimal / centesimal (... repetição padrão de nomenclatura ...) 110 - decacentimal 111 - unodecacentimal ( ... repetição padrão de nomenclatura ...) 200 - bicentimal / bicentesimal (... repetição de nomeação padrão ...) 210 - decabicentimal 211 - unodecabicentimal (... repetição de nomeação padrão ...) 300 - tercentimal / tricentesimal 400 - quattrocentimal / quadricentesimal 500 - quincentimal / pentacentesimal 600 - hexacentimal / hexacentesimal 700 - heptacentimal / heptacentesimal 800 - octacentimal / octocentimal / octacentesimal / octocentesimal 900 - novacentimal / novacentesimal 1000 - millesimal 2000 - bimillesimal (... repetição padrão de nomenclatura ...) 10000 - decamillesimal Sistemas posicionais em detalhe
Em um sistema de b base- posicional numeral (com b um positivo número natural conhecido como o radix), símbolos de base B (ou dígitos) correspondentes aos primeiros números naturais b incluindo zero são usadas. Para gerar o resto dos números, a posição do símbolo na figura é usado. O símbolo na última posição tem o seu próprio valor, e como ele se move ao seu valor esquerda é multiplicado por b.
Por exemplo, no casa decimal do sistema (base de 10), os meios 4327 numeral (4 × 10 3) + (3 x 10 2) + (2 x 10 1) + (7 × 10 0), notando que 10 0 = 1 .
Em geral, se b é a base, podemos escrever um número no sistema de numeração de base b ao expressá-la sob a forma de um n b n + um n - 1 b n - + 1 a n - 2 b n - 2 +. .. + a 0 b 0 e escrevendo os dígitos enumerados um a n n - 1 a n - 2 ... um 0 em ordem decrescente. Os dígitos são números naturais entre 0 e b - 1, inclusive.
Se um texto (como este) discute várias bases, e se existe ambigüidade, a base (que é representada, em base 10) é adicionado em subscrito à direita do número, assim: base numérica. A menos que especificado pelo contexto, os números sem subscrito são considerados decimal.
Ao utilizar um ponto de dividir os dígitos em dois grupos, também se pode escrever fracções do sistema de posicionamento. Por exemplo, a base 2 numeral indica a 10,11 1 × 2 × 1 + 0 0 + 1 2 × 2 × -1 + 1 2 -2 = 2,75.
Em geral, os números no sistema base b são da forma:
O número b k e b - k são o pesos dos dígitos correspondentes. A posição k é o logaritmo do peso correspondente w, que é 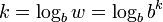 . A posição mais alta utilizada é perto do ordem de grandeza do número.
. A posição mais alta utilizada é perto do ordem de grandeza do número.
O número de marcas de registro necessária no sistema numeral unary para descrever o peso teria sido w. No sistema de posicionamento o número de dígitos necessária para descrever é apenas 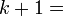
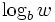
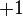 , Para
, Para 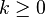 . Por exemplo, para descrever o peso 4 dígitos 1000, em seguida, são necessários uma vez
. Por exemplo, para descrever o peso 4 dígitos 1000, em seguida, são necessários uma vez 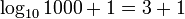 . O número de dígitos necessário para descrever a posição é
. O número de dígitos necessário para descrever a posição é 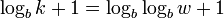 (Nas posições 1, 10, 100 ... apenas para simplicidade no exemplo decimal).
(Nas posições 1, 10, 100 ... apenas para simplicidade no exemplo decimal).
| Posição | 3 | 2 | 1 | 0 | -1 | -2 | ... |
|---|---|---|---|---|---|---|---|
| Peso | 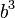 | 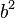 | 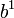 | 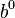 | 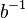 | 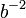 | ... |
| Dígito |  | 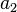 | 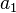 | 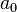 | 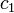 | 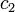 | ... |
| Decimal peso exemplo | 1000 | 100 | 10 | 1 | 0,1 | 0,01 | ... |
| Decimal exemplo dígitos | 4 | 3 | 2 | 7 | 0 | 0 | ... |
Note-se que um número tem uma terminação ou repetir expansão se e somente se é racional ; esta não depende da base. Um número que termina em uma base pode repetir em outro (0,3 assim 10 = ,0100110011001 ... 2). Um número irracional permanece unperiodic (quantidade infinita de dígitos unrepeating) em todas as bases integrais. Assim, por exemplo, na base 2, π = 3,1415926 ... 10 pode ser baixado para o unperiodic 11,001001000011111 ... 2.
Se b = p é um número primo , pode-se definir números p base- cuja expansão à esquerda nunca pára; estes são chamados a números p-adic.
Mudança de raiz
Um simples algoritmo para converter números inteiros entre radices positivo inteiros é repetido divisão pela raiz alvo; os restos dar os "dígitos" de partida, pelo menos significativa. Por exemplo, 1020304 base 10 na base 7:
1020304/7 = 145757 R5
145757/7 20822 = R3
20822/7 = 2,974 R4
2974/7 = 424 R6
424/7 = 60 r 4
60/7 = 8 R4
8/7 = 1 1 r
1/7 = 0 R1 => 11.446.435
Por exemplo, 10110111 base 2 em 5 de base:
10110111/101 = 100100 r 11 (3)
100100/101 = 111 r 1 (1)
111/101 = 1 R 10 (2)
1/101 = 0 r 1 (1) => 1213
Para converter uma fração "decimal", faça multiplicação repetida, tendo as partes salientes inteiros como os "dígitos". Infelizmente, uma fração de terminação em uma base pode não terminar em outro. Por exemplo, base 0.1A4C 16 em base 9:
0.1A4C × 9 = 0.ECAC 0.ECAC × 9 = 8.520C 0.520C × 9 = 2.E26C 0.E26C × 9 = 7.F5CC 0.F5CC × 9 = 8.A42C 0.A42C × 9 = 5. C58C => 0,082785 ...
Inteiros de comprimento variável generalizadas
Mais geral está usando uma notação (aqui escrito little-endian) como 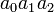 para
para 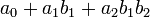 , Etc.
, Etc.
Este é utilizado em punycode, um aspecto da qual é a representação de uma sequência de números inteiros não negativos de tamanho arbitrário sob a forma de uma sequência sem delimitadores, de "dígitos" de uma colecção de 36: az e 0-9, 0-25 e representando 26-35, respectivamente. Um dígito inferior a um valor limiar de marca que é o digito mais significativo, por conseguinte, a fim de o número. O valor limiar depende da posição do número. Por exemplo, se o valor limite para o primeiro dígito é b (isto é, 1), em seguida, um (ou seja, 0) marca o fim da série (que tem apenas um dígito), de modo em número de mais de um dígito da gama é apenas b -9 (1-35), por conseguinte, o peso é 1 b 35 em vez de 36. Suponhamos que os valores de limiar para o segundo e terceiro dígitos são C (2), em seguida, o terceiro dígito tem um peso de 34 × 35 = 1190 e que têm a seguinte seqüência:
A (0), ba (1), CA (2), .., 9a (35), BB (36), CB (37), .., 9b (70), o BCA (71), .., 99A (1260), o BCB (1261), etc.
Note-se que ao contrário de um-35 de base do sistema numeral regular, temos números como 9b, onde 9 e B representam cada um 35; no entanto, a representação é único porque ac e aca não são permitidos.
A flexibilidade na escolha de valores de limite permite a otimização de acordo com a frequência de ocorrência dos números de vários tamanhos.
O caso de todos os valores de limiar igual a 1 corresponde a bijective numeração, onde os zeros correspondem a separadores de números com dígitos que são diferentes de zero.
Propriedades de sistemas numéricos com bases inteiros
Sistemas de numeração com a base A, onde A é um número inteiro positivo, possuem as seguintes propriedades:
- Se A é mesmo e A / 2 é ímpar, todos os poderes integrais maior que zero do número (A / 2) 1 irá conter (A / 2) 1 como seu último dígito
- Se tanto A como A / 2 são ainda, em seguida, todos os poderes integrais maior do que ou igual a zero do número (A / 2) 1 alternará entre ter (A / 2) 1 e 1 como seu último dígito. (Para potências ímpares será (A / 2) 1, mesmo para potências será 1)
A prova da primeira propriedade:
Definir 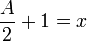 Em seguida, x é par, e todos
Em seguida, x é par, e todos 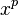 para p maior que 0 deve ser mesmo. A propriedade é equivalente a
para p maior que 0 deve ser mesmo. A propriedade é equivalente a
Nós verificar primeiro o caso para p = 1
x é inferior a A, então o resultado é trivial. Em seguida, vá para p = 2:
Desde 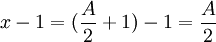 , Em seguida, para todos, mesmo N:
, Em seguida, para todos, mesmo N:
Como x é par, em seguida, 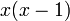 é congruente a zero Um módulo. Portanto:
é congruente a zero Um módulo. Portanto:
Usando indução, assumindo que a propriedade é válida para p -1:
Uma vez que o processo é válido para p -1, então 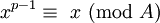 . Desde
. Desde
é um exemplo da Equação 1, em seguida 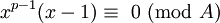 . Isto deixa, para todos os p maior do que 0,
. Isto deixa, para todos os p maior do que 0,
QED
A prova da segunda propriedade:
Definir 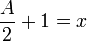 Então x é estranho, e tudo
Então x é estranho, e tudo 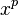 para P maior do que ou igual a 0 deve ser ímpar. A propriedade é equivalente a
para P maior do que ou igual a 0 deve ser ímpar. A propriedade é equivalente a
Desde 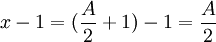 , Em seguida, para todos E estranho:
, Em seguida, para todos E estranho:
O caso está marcada primeiro para p = 0:
Este resultado é trivial
Em seguida, para P = 1:
Esse resultado também é trivial
Em seguida, para p = 2:
Como x é ímpar, então x (x-1) é um exemplo da Equação 2,
Em seguida, para p = 3:
Porque 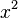 é estranho,
é estranho, 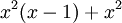 é um exemplo da Equação 2,
é um exemplo da Equação 2,
Desde 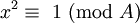 ,
,
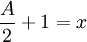 , Assim
, Assim 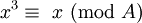 .
.
Usando indução, assumindo que a propriedade é válida para p -1:
Se p for ímpar:
Desde 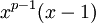 é um exemplo da Equação (2),
é um exemplo da Equação (2), 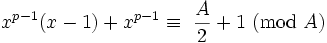 , Assim
, Assim
Se p for mesmo:
Desde 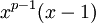 é um exemplo da Equação (2),
é um exemplo da Equação (2), 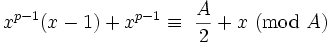 .
.

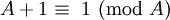 , Assim
, Assim
QED