Emmy Noether
Antecedentes de las escuelas de Wikipedia
SOS ofrecen una descarga completa de esta selección de escuelas para su uso en escuelas intranets. El patrocinio de los niños ayuda a los niños en el mundo en desarrollo para aprender también.
| Emmy Noether | |
|---|---|
 | |
| Nacido | Amalie Emmy Noether 23 de marzo 1882 Erlangen, Baviera, Alemania |
| Murió | 14 de abril 1935 (53 años) Bryn Mawr, Pennsylvania, EE.UU. |
| Nacionalidad | Alemán |
| Campos | Matemáticas y Física |
| Instituciones | Universidad de Göttingen Bryn Mawr College |
| Alma máter | Universidad de Erlangen |
| Doctoral consejero | Paul Gordan |
| Los estudiantes de doctorado | Max Deuring Hans Fitting Grete Hermann Zeng Jiongzhi Jacob Levitzki Otto Schilling Ernst Witt |
| Conocido por | Resumen álgebra La física teórica |
Emmy Noether (alemán: [Nøːtɐ]; nombre oficial Amalie Emmy Noether, marzo 23, 1882 hasta abril 14, 1935), fue un influyente Alemán matemático conocido por sus contribuciones pioneras a álgebra abstracta y la física teórica. Descrito por Pavel Alexandrov, Albert Einstein , Jean Dieudonné, Hermann Weyl, Norbert Wiener y otros como la mujer más importante en la historia de las matemáticas, que revolucionó las teorías de anillos, campos, y álgebras. En física, El teorema de Noether explica la conexión fundamental entre simetría y leyes de conservación.
Ella nació en una familia judía en la Ciudad bávara de Erlangen; su padre era matemático Max Noether. Emmy originalmente planeado para enseñar el francés y el Inglés después de pasar los exámenes requeridos, sino que estudió matemáticas en la Universidad de Erlangen, donde su padre dio una conferencia. Después de completar su tesis doctoral en 1907 bajo la supervisión de Paul Gordan, trabajó en el Instituto Matemático de Erlangen sin goce de sueldo durante siete años (en el momento de las mujeres fueron excluidas en gran parte de los puestos académicos). En 1915, fue invitada por David Hilbert y Felix Klein a unirse al departamento de matemáticas en la Universidad de Göttingen, un centro de renombre mundial de la investigación matemática. La facultad de filosofía se opuso, sin embargo, y ella pasó cuatro años dando conferencias bajo el nombre de Hilbert. Su habilitación fue aprobada en 1919, lo que le permite obtener el grado de Privatdozent.
Noether siguió siendo un destacado miembro de la Göttingen departamento de matemáticas hasta 1933; sus estudiantes a veces se llaman los "chicos Noether". En 1924, el matemático holandés BL van der Waerden se unió a su círculo y pronto se convirtió en el expositor de liderazgo de ideas de Noether: su trabajo fue la base para el segundo volumen de su influyente libro de texto de 1931, Moderne Algebra. En el momento de su discurso en sesión plenaria en el 1932 Congreso Internacional de Matemáticos en Zürich , su perspicacia algebraica fue reconocido en todo el mundo. Al año siguiente, el gobierno nazi de Alemania rechazó Judios de cargos universitarios y Noether se trasladó a Estados Unidos para ocupar un puesto en Bryn Mawr College en Pennsylvania. En 1935 se sometió a una cirugía para un quiste de ovario y, a pesar de los signos de recuperación, murió cuatro días más tarde a la edad de 53.
Trabajo matemático de Noether se ha dividido en tres "épocas". En la primera (1908- 19 ), hizo importantes contribuciones a la teoría de invariantes algebraicos y campos de número. Su trabajo sobre los invariantes diferenciales en el cálculo de variaciones , El teorema de Noether, ha sido llamado "uno de los teoremas matemáticos más importantes jamás probados en la orientación del desarrollo de la física moderna". En la segunda época (1920- 26 ), comenzó el trabajo que "cambió la faz del álgebra [abstract]". En su artículo clásico Idealtheorie en Ringbereichen (Teoría de ideales en Anillo Dominios, 1921) Noether desarrolló la teoría de ideales en anillos conmutativos en una poderosa herramienta con aplicaciones de amplio alcance. Hizo uso elegante de la ascendiendo condición de cadena y objetos satisfacerla se nombran Noetheriano en su honor. En la tercera época (1927- 35 ), publicó importantes obras en álgebras no conmutativas y números hipercomplejos y unidos el teoría de la representación de los grupos con la teoría de módulos e ideales. Además de sus propias publicaciones, Noether fue generoso con sus ideas y se acredita con varias líneas de investigación publicados por otros matemáticos, incluso en campos muy alejados de su trabajo principal, como topología algebraica.
Biografía

El padre de Emmy, Max Noether, era descendiente de una familia de comerciantes al por mayor en Alemania. Él había estado paralizado por la poliomielitis a la edad de catorce años. Recuperó la movilidad, pero una pierna quedó afectada. En gran parte autodidacta, fue galardonado con un Doctor por la Universidad de Heidelberg en 1868. Después de enseñar allí durante siete años, él tomó una posición en la ciudad bávara de Erlangen, donde conoció y se casó con Ida Amalia Kaufmann, la hija de un próspero comerciante. Contribuciones matemáticas de Max Noether debían geometría algebraica principalmente, siguiendo los pasos de Alfred Clebsch. Sus mejores resultados conocidos son el Brill-Noether teorema y el residuo, o Teorema AF + BG; varios otros teoremas se asocian con él, incluyendo El teorema de Noether Max.
Emmy Noether nació el 23 de marzo de 1882, el primero de cuatro hijos. Su primer nombre fue "Amalie", después de que su madre y su abuela paterna, pero ella comenzó a usar su segundo nombre a una edad temprana. Cuando era niña, ella era muy querido. Ella no se destacan académicamente a pesar de que era conocido por ser inteligente y amigable. Emmy fue miope y hablado con un menor de edad ceceo durante la infancia. Un amigo de la familia relató una historia años más tarde acerca joven Emmy resolver rápidamente un desafío para la mente en una fiesta infantil, mostrando perspicacia lógicas a esa temprana edad. Emmy se le enseñó a cocinar y limpiar, al igual que la mayoría de las niñas de la época, y ella tomó clases de piano. Ella siguió ninguna de estas actividades con pasión, a pesar de que le encantaba bailar.
Tenía tres hermanos menores. El mayor, Alfred, nació en 1883, fue galardonado con un doctorado en química de Erlangen en 1909, pero murió nueve años más tarde. Fritz Noether, nacido en 1884, es recordado por sus logros académicos: después de estudiar en Múnich hizo una reputación por sí mismo en las matemáticas aplicadas . El más joven, Gustav Robert, nació en 1889. Se sabe muy poco acerca de su vida; que padecía una enfermedad crónica y murió en 1928.
Universidad de Erlangen

Emmy Noether mostró dominio temprano en francés e Inglés. En la primavera de 1900 tomó el examen para profesores de idiomas y recibió un puntaje general de sehr gut (muy bueno). Su actuación le calificado para enseñar idiomas en las escuelas reservadas a las niñas, pero ella prefirió continuar sus estudios en la Universidad de Erlangen.
Esta fue una decisión poco convencional; dos años antes, el Senado Académico de la universidad había declarado que permitir Coeducación sería "derrocar todo orden académico". Una de las dos únicas mujeres estudiantes en una universidad de 986, Noether sólo se le permitió clases de auditoría en lugar de participar plenamente, y requiere el permiso de los profesores individuales cuyas conferencias deseaba asistir. A pesar de los obstáculos, el 14 de julio de 1903 aprobó el examen de graduación en un Realgymnasium en Nuremberg.
Durante el semestre de invierno 1903-1904, estudió en la Universidad de Göttingen, asistiendo a conferencias impartidas por el astrónomo Karl Schwarzschild y matemáticos Hermann Minkowski, Otto Blumenthal, Felix Klein y David Hilbert . Poco después, se rescindieron restricciones a la participación de las mujeres en esa universidad.
Noether regresó a Erlangen. Ella volvió a entrar en la universidad oficialmente el 24 de octubre de 1904, y declaró su intención de centrarse exclusivamente en las matemáticas. Bajo la supervisión de Paul Gordan escribió su disertación, Über die Bildung Formensystems der ternären biquadratischen Formulario des (en sistemas completos de invariantes para las formas ternario Bicuadráticos, 1907). A pesar de que había sido bien recibido, Noether más tarde describió su tesis como "basura".
Para los próximos siete años (1908- 15 ) enseñó en la Universidad de Instituto de Matemáticas de Erlangen sin goce de sueldo, de vez en cuando en sustitución de su padre cuando él estaba demasiado enfermo para dar una conferencia. En 1910 y 1911 publicó una extensión de su trabajo de tesis a partir de tres variables para n variables.

Gordan retiró en la primavera de 1910, pero continuó enseñando vez en cuando con su sucesor, Erhard Schmidt, que abandonó poco después para un puesto en Breslau. Gordan retiró de la enseñanza por completo en 1911 con la llegada del sucesor de Schmidt Ernst Fischer, y murió en diciembre 1912.
De acuerdo a Hermann Weyl, Fischer era una influencia importante en Noether, en particular, mediante la introducción de ella para el trabajo de David Hilbert . De 1913 a 1916 Noether publicó varios artículos que se extienden y aplican métodos de Hilbert a objetos matemáticos como campos de funciones racionales y la invariantes de grupos finitos. Esta fase marca el comienzo de su compromiso con el álgebra abstracta , el campo de las matemáticas a lo que ella haría contribuciones pioneras.
Noether y Fischer compartieron animado disfrute de las matemáticas y con frecuencia discuten conferencias mucho después de que habían terminado; Noether es conocido por haber enviado postales a Fischer continuar el hilo de sus pensamientos matemáticos.
Universidad de Göttingen
En la primavera de 1915, Noether fue invitado a regresar a la Universidad de Gotinga por David Hilbert y Felix Klein. Su esfuerzo para reclutar a ella, sin embargo, fue bloqueado por el filólogos y historiadores entre la facultad de filosofía: las mujeres, insistieron, no debe convertirse en privatdozent. Un miembro de la facultad protestó: "¿Qué van a pensar nuestros soldados cuando regresan a la universidad y encuentran que están obligados a aprender a los pies de una mujer?" Hilbert respondió con indignación, diciendo: "No veo que el sexo del candidato es un argumento en contra de su admisión como privatdozent. Después de todo, somos una universidad, no un baño de la casa."

Noether fue a Göttingen a finales de abril; dos semanas más tarde su madre murió repentinamente en Erlangen. Ella ya había recibido atención médica para una condición del ojo, pero su naturaleza e impacto en su muerte es desconocida. Casi al mismo tiempo el padre de Noether se retiró y su hermano se unió al Ejército alemán para servir en la Primera Guerra Mundial . Ella volvió a Erlangen durante varias semanas, sobre todo para cuidar a su anciano padre.
Durante sus primeros años de enseñanza en Göttingen ella no tiene una posición oficial y no se pagó; su familia pagó por su alojamiento y comida y apoyó su trabajo académico. Sus conferencias a menudo se anuncian bajo el nombre de Hilbert, y Noether proporcionarían "asistencia".
Poco después de llegar a Göttingen, sin embargo, ella demostró sus capacidades, demostrando el teorema ahora conocido como El teorema de Noether, que muestra que una ley de conservación se asocia con cualquier diferenciable la simetría de un sistema físico. Físicos estadounidenses Leon M. Lederman y Christopher T. Hill argumentan en su libro La simetría y el Universo hermoso que el teorema de Noether es "sin duda uno de los teoremas matemáticos más importantes jamás probados para guiar el desarrollo de la física moderna, posiblemente, a la par con el teorema de Pitágoras ".

Cuando la Primera Guerra Mundial terminó, la Revolución alemana de 1918-1919 trajo un cambio significativo en las actitudes sociales, incluyendo más derechos para las mujeres. En 1919 la Universidad de Gotinga permitió Noether para proceder con ella habilitación (elegibilidad para la tenencia). Su examen oral se celebró a finales de mayo, y se entregó con éxito su conferencia habilitación en junio.
Tres años después, recibió una carta de la Ministro prusiano de Ciencia, Arte y Educación Pública, en la que le confirió el título de Profesor nicht beamteter ausserordentlicher (profesor sin plaza fija con derechos administrativos internos limitados y funciones). Esta fue una cátedra no remunerado "extraordinaria", no el más alto cátedra "ordinario", que era una posición de servicio civil. Aunque reconoció la importancia de su trabajo, la posición todavía proporciona ningún salario. Noether no fue pagado sus clases hasta que fue nombrado para el cargo especial de Lehrbeauftragte für Algebra un año después.
Obra fundamental en álgebra abstracta
Aunque el teorema de Noether tuvo un efecto profundo en la física, entre los matemáticos que ella es mejor recordado por sus contribuciones fundamentales a álgebra abstracta . Como Nathan Jacobson dice en su introducción a los Collected Papers de Noether,
El desarrollo del álgebra abstracta, que es una de las innovaciones más distintivas de las matemáticas del siglo XX, se debe en gran parte a ella - en los trabajos publicados, en conferencias, y en la influencia personal sobre sus contemporáneos.
Innovador trabajo de Noether en álgebra comenzó en 1920. En colaboración con W. Schmeidler, que luego publicó un artículo acerca de la la teoría de los ideales en los que definen los ideales de izquierda y derecha en un anillo. Al año siguiente se publicó un documento histórico llamado Idealtheorie en Ringbereichen, analizando ascendiendo condiciones de la cadena con respecto a los ideales (matemáticos). Algebraist señalado Irving Kaplansky llama este trabajo "revolucionario"; la publicación dio lugar a la expresión " Anillo noetheriano ", y varios otros objetos matemáticos que se denominan Noetheriano.
En 1924 un joven matemático holandés, BL van der Waerden, llegó a la Universidad de Gotinga. De inmediato comenzó a trabajar con Noether, que proporciona métodos invaluables de la conceptualización abstracta. van der Waerden dijo más tarde que su originalidad era "absoluta más allá de comparación". En 1931 publicó Moderne Algebra, un texto central en el campo; su segundo tomo prestado pesadamente del trabajo de Noether. Aunque Emmy Noether no buscó reconocimiento, incluyó como una nota en la séptima edición ", basada en parte en conferencias a cargo de E. Artin y E. Noether ". A veces se les permite a sus colegas y estudiantes para recibir crédito por sus ideas, ayudándoles a desarrollar sus carreras a costa de la suya propia.
visita van der Waerden era parte de una convergencia de los matemáticos de todo el mundo a Göttingen, que se convirtió en un importante centro de investigación matemática y física. Desde 1926 hasta 1930 Rusia topólogo Pavel Alexandrov dio una conferencia en la universidad, y él y Noether rápidamente se convirtió en buenos amigos. Él comenzó a referirse a ella como der Noether, utilizando el artículo alemán masculino como una expresión de cariño para mostrar su respeto. Trató de organizar para él para obtener un puesto en Göttingen como profesor regular, pero sólo fue capaz de ayudarle a asegurar una beca de la Fundación Rockefeller. Se reunieron con regularidad y disfrutaron de las discusiones acerca de las intersecciones de álgebra y topología. En su discurso conmemorativo 1935, Alexandrov nombrado Emmy Noether "la mujer más grande matemático de todos los tiempos".
Docencia y estudiantes
En Gotinga, Noether supervisó más de una docena de estudiantes de doctorado; su primera era Grete Hermann, quien defendió su tesis en febrero de 1925. Más tarde se habló reverentemente de su "madre disertación" .. Noether también supervisó Max Deuring, que se distinguió como estudiante y pasó a contribuir de manera significativa al campo de la geometría aritmética; Hans Fitting, recordado por Montaje del teorema y la Lema de montaje; y Zeng Jiongzhi (también traducida como "Chiungtze C. Tsen" en Inglés), que demostró El teorema de Tsen. También trabajó en estrecha colaboración con Wolfgang Krull, quien avanzó enormemente álgebra conmutativa con su Hauptidealsatz y su teoría de la dimensión de los anillos conmutativos.
Además de su visión matemática, Noether fue respetada por su consideración hacia los demás. A pesar de que a veces actuaba con rudeza hacia los que no estaba de acuerdo con ella, sin embargo, ganó una reputación de amabilidad constante y paciente guía de los nuevos estudiantes. Su lealtad a la precisión matemática causó un colega llamarla "un crítico severo", pero ella combinó esta exigencia de precisión con una actitud de protección. Un colega más tarde la describió de esta manera: "Completamente unegotistical y libre de vanidad, ella nunca dijo nada por sí misma, pero promovió las obras de sus estudiantes por encima de todo."
Su estilo de vida frugal en un primer momento se debió al pago de la denegación por su trabajo; Sin embargo, incluso después de la universidad comenzó a pagar ella un pequeño salario en 1923, ella continuó viviendo una vida sencilla y modesta. Le pagaron más generosamente más tarde en su vida, pero la mitad ahorrado de su salario para legar a su sobrino, Gottfried E. Noether.
Mayormente despreocupado por la apariencia y modales, se centró en sus estudios a la exclusión de romance y moda. Un algebraist distinguido Olga Taussky-Todd describió un almuerzo, durante el cual Noether, totalmente absorto en una discusión de las matemáticas, "gesticulaba salvajemente" mientras comía y "derramó su comida constantemente y lo borró de su vestido, completamente imperturbable". Estudiantes-Aspecto consciente encogían mientras recogía el pañuelo de su blusa y ignoró la creciente desorden de su cabello durante una conferencia. Dos alumnas una vez que se acercaron a ella durante un descanso en una clase de dos horas para expresar su preocupación, pero no fueron capaces de romper a través de la discusión matemática enérgico que tenía con otros estudiantes.
Según obituario van der Waerden de Emmy Noether, ella no siguió un plan de lección para sus conferencias, que frustraron algunos estudiantes. En cambio, ella usó sus conferencias como un tiempo de discusión espontánea con sus alumnos, para pensar y aclarar importantes problemas de vanguardia en las matemáticas. Algunos de sus resultados más importantes se desarrollaron en estas conferencias, y las notas de clase de sus estudiantes formaron la base para varios libros de texto importantes, como los de van der Waerden y Deuring.
Varios de sus colegas asistieron a sus conferencias, y se permitió algunas de sus ideas, como la producto cruzado (verschränktes Produkt en alemán) de álgebras asociativas, que será publicado por otros. Noether fue recordado por haber dado al menos cinco cursos semestrales en Göttingen:
- Invierno 1924-1925: Gruppentheorie und hyperkomplexe Zahlen (teoría de grupos y hipercomplejos Números)
- Invierno 1927-1928: Hyperkomplexe Grössen und Darstellungstheorie (Cantidades hipercomplejos y Representación Teoría)
- Verano 1928: Nichtkommutative Algebra (Álgebra no conmutativa)
- Verano 1929: Nichtkommutative Arithmetik (no conmutativa Aritmética)
- Invierno 1929-1930: Algebra der hyperkomplexen Grössen (Álgebra de Cantidades hipercomplejos).
Estos cursos a menudo precedidos principales publicaciones en estas áreas.
Noether hablaba rápidamente, lo que refleja la velocidad de sus pensamientos, muchos dijeron, y exigió una gran concentración de sus estudiantes. Los estudiantes que disgustaba su estilo a menudo se sentían alienados. Algunos alumnos sintieron que ella dependía demasiado de las discusiones espontáneas. Sus estudiantes más dedicados, sin embargo, disfrutaron el entusiasmo con que se acercaba a las matemáticas, sobre todo porque sus conferencias construyen a menudo en trabajos anteriores que habían hecho juntos.
Ella desarrolló un estrecho círculo de colegas y estudiantes que pensaban de forma similar y tendían a excluir a los que no lo hicieron. "Outsiders" que ocasionalmente visitaban conferencias de Noether solían pasar a sólo 30 minutos en la sala antes de salir de la frustración o la confusión. Un estudiante regular, dijo de uno de esos casos: "El enemigo ha sido derrotado, sino que ha limpiado."
Noether mostró una devoción a su objeto y sus estudiantes que se extendían más allá de la jornada académica. Una vez, cuando el edificio estaba cerrado por un feriado estatal, reunió la clase en la escalinata exterior, los condujo por el bosque, y dio una conferencia en un café local. Más tarde, después de que ella había sido despedido por el Tercer Reich , invitó a los estudiantes a su casa para hablar de sus planes para el futuro y conceptos matemáticos.
Moscú

En el invierno de 1928-1929 Noether aceptó una invitación para La Universidad Estatal de Moscú, donde continuó trabajando con PS Alexandrov. Además de llevar adelante con su investigación, ella daba clases en álgebra abstracta y geometría algebraica. Trabajó con los topologists, Lev Pontryagin y Nikolai Chebotaryov, que más tarde elogió sus contribuciones al desarrollo de la teoría de Galois .
Aunque la política no era el centro de su vida, Noether tuvo un gran interés en los asuntos políticos y, según Alexandrov, mostró un considerable apoyo a la Revolución Rusa (1917) . Ella estaba especialmente feliz de ver soviéticos avances en los campos de la ciencia y las matemáticas, que ella consideraba indicativo de nuevas oportunidades que ofrece el Proyecto bolchevique. Esta actitud hizo que sus problemas en Alemania, culminando en su desahucio de una edificio de alojamiento de pensiones, después de que líderes estudiantiles se quejó de vivir con "una judía-marxista apoyado".

Noether planeaba regresar a Moscú, un esfuerzo por la que recibió el apoyo de Alexandrov. Después de que ella abandonó Alemania en 1933 trató de ayudarla a obtener una cátedra en la Universidad Estatal de Moscú a través del Soviética Ministerio de Educación. Aunque este esfuerzo no tuvo éxito, que se correspondían con frecuencia durante la década de 1930, y en 1935 se hicieron planes para un regreso a la Unión Soviética. Mientras tanto, su hermano, Fritz aceptó un puesto en el Instituto de Investigación de Matemáticas y Mecánica en Tomsk, en el Distrito Federal de Siberia de Rusia, después de perder su puesto de trabajo en Alemania.
Reconocimiento
En 1932 Emmy Noether y Emil Artin recibió el Ackermann-Teubner Memorial Award por sus contribuciones a las matemáticas. El premio lleva una recompensa monetaria de 500 Marcos del Reich y fue visto como un reconocimiento oficial a largo atraso de su importante labor en el campo. Sin embargo, sus colegas expresaron su frustración por el hecho de que no fue elegido para el Göttingen Gesellschaft der Wissenschaften (Academia de Ciencias) y nunca fue promovido a la posición de Ordentlicher profesor (profesor titular).

Colegas de Noether celebran sus cincuenta años en 1932, en estilo matemáticos típicos ". Helmut Hasse dedica un artículo a ella en el Mathematische Annalen, en el que él le confirmó la sospecha de que algunos aspectos de álgebra no conmutativa son más simples que los de álgebra conmutativa, demostrando un no conmutativa ley de reciprocidad. Esto agradó inmensamente. También le envió un acertijo matemático, el "mμν-enigma de sílabas", que se resolvió de inmediato; el enigma se ha perdido.
En noviembre del mismo año, Noether pronunció un discurso en sesión plenaria (Vortrag großer) sobre "los sistemas Hyper-complejos en sus relaciones con conmutativa álgebra y la teoría de números" en la Congreso Internacional de Matemáticos en Zürich . El congreso contó con la presencia de 800 personas, entre colegas de Noether Hermann Weyl, Edmund Landau, y Wolfgang Krull. Hubo 420 participantes oficiales y veintiún direcciones plenarias presentadas. Al parecer, la posición prominente habla de Noether fue un reconocimiento de la importancia de sus contribuciones a las matemáticas. El 1932 el congreso se describe a veces como el punto más alto de su carrera.
Expulsión de Göttingen
Cuando Adolf Hitler se convirtió en el Reichskanzler alemán en enero de 1933, los nazis la actividad en todo el país aumentó de forma espectacular. En la Universidad de Gotinga la Asociación de Estudiantes alemán lideró el ataque contra el "espíritu no alemán" atribuida a Judios y fue ayudado por un privatdozent nombrado Werner Weber, un antiguo alumno de Emmy Noether. Actitudes antisemitas crearon un clima hostil a profesores judíos. Un manifestante joven según los informes exigió: "los estudiantes arios quieren matemáticas arias y las matemáticas no judíos."
Una de las primeras acciones del gobierno de Hitler fue la Ley para la Restauración del Servicio Civil Profesional que suprimía Judios y empleados del gobierno políticamente sospechosos (incluyendo profesores universitarios) de sus puestos de trabajo a menos que había "demostrado su lealtad a Alemania" por servir en la Primera Guerra Mundial I. En abril de 1933 Noether recibió una notificación por parte de el Ministerio Prusiano de Ciencias, Arte y Educación Pública, que decía: "Sobre la base del párrafo 3 del Código de la Función Pública de 7 de abril de 1933, por la presente se retiran de que el derecho a enseñar en la Universidad de Gotinga." Varios de sus colegas de Noether, incluyendo Max Born y Richard Courant, también tenía sus posiciones revocados. Noether aceptó la decisión con calma, el apoyo a otros durante este tiempo difícil. Hermann Weyl escribió más tarde que "Emmy Noether-su coraje, su franqueza, su despreocupación acerca de su propio destino, su espíritu conciliador, estaba en medio de todo el odio y la mezquindad, la desesperación y la tristeza que nos rodea, un consuelo moral." Típicamente, Noether siguió centrada en las matemáticas, la recopilación de los estudiantes en su apartamento para discutir la teoría de campos de clase. Cuando uno de sus alumnos apareció en el uniforme de la organización paramilitar nazi Sturmabteilung (SA), ella no mostraba signos de agitación y, al parecer, incluso se rió de ello más tarde.
Bryn Mawr

Como decenas de profesores nuevos desempleados comenzaron a buscar posiciones fuera de Alemania, sus colegas en los Estados Unidos trataron de proporcionar asistencia y oportunidades de empleo para ellos. Albert Einstein y Hermann Weyl fueron nombrados por el Instituto de Estudios Avanzados de Princeton, mientras que otros se esforzaron por encontrar un patrocinador requerido para legal la inmigración. Noether fue contactado por representantes de dos instituciones educativas, Bryn Mawr College en los Estados Unidos y Somerville College de la Universidad de Oxford en Inglaterra. Tras una serie de negociaciones con el Fundación Rockefeller, una subvención a Bryn Mawr fue aprobado para Noether y ella tomó una posición allí, comenzando a finales de 1933.
En Bryn Mawr, Noether conoció y entabló amistad Anna Wheeler, que había estudiado en Gotinga justo antes de Noether llegó allí. Otra fuente de apoyo en el colegio era el presidente de Bryn Mawr, Marion Edwards Park, que con entusiasmo invitó a los matemáticos en la zona de "ver Dr. Noether en acción!" Noether y un pequeño equipo de estudiantes trabajaron rápidamente a través de van der Waerden 1930 libro Moderne Algebra I y partes de De Erich Hecke Theorie der algebraischen Zahlen (Teoría de números algebraicos, 1908).
En 1934, Noether comenzó a dar clases en el Instituto de Estudios Avanzados de Princeton por invitación de Abraham Flexner y Oswald Veblen. También trabajó con y supervisado Abraham Albert y Harry Vandiver. Sin embargo, ella comentó acerca de la Universidad de Princeton que no era bienvenida en la "universidad de los hombres, donde se admite nada femenina".
Su tiempo en los Estados Unidos era agradable, rodeado como estaba por colegas de apoyo y absorta en sus temas favoritos. En el verano de 1934 regresó brevemente a Alemania para ver Emil Artin y su hermano Fritz antes de irse a Tomsk. Aunque muchos de sus antiguos compañeros habían sido expulsados de las universidades, ella fue capaz de utilizar la biblioteca como un "erudito extranjero".
Muerte

En abril 1935 los médicos descubrieron un tumor en Noether de pelvis. Preocupado por las complicaciones de la cirugía, ordenaron dos días de reposo en cama primero. Durante la operación, descubrieron un quiste ovárico "del tamaño de un gran melón ". Dos tumores más pequeños en su útero parecía ser benigna y no se eliminaron, para evitar la prolongación de la cirugía. Durante tres días se apareció a convalecer normalmente, y ella se recuperó rápidamente de una colapso circulatorio en el cuarto. El 14 de abril se quedó inconsciente, su temperatura se elevó a 109 ° F (42.8 ° C), y ella murió. "[E] s no es fácil decir lo que había ocurrido en el Dr. Noether", uno de los médicos escribieron. "Es posible que haya habido algún tipo de infección inusual y virulenta, que golpeó la base del cerebro, donde se supone que los centros de calor que se encuentra."
Pocos días después de la muerte de Noether sus amigos y asociados en Bryn Mawr celebraron una pequeña ceremonia conmemorativa en la casa de la universidad President Park. Hermann Weyl y Richard Brauer viajó desde Princeton y habló con Wheeler y Taussky sobre su colega fallecido. En los meses que siguieron, homenajes escritos comenzaron a aparecer en todo el mundo: Albert Einstein unió van der Waerden, Weyl, y Pavel Alexandrov en el pago de sus aspectos. Su cuerpo fue incinerado y las cenizas enterrado bajo la pasarela alrededor de los claustros de la M. Carey Thomas Library en el Bryn Mawr.
Las contribuciones a las matemáticas y la física
En primer lugar Noether es recordado por los matemáticos como un algebrista y por su trabajo en la topología . Los físicos aprecian lo mejor para ella famoso teorema debido a sus consecuencias de largo alcance para la física teórica y sistemas dinámicos. Ella mostró una propensión aguda para el pensamiento abstracto, lo que le permitió acercarse a los problemas de las matemáticas de una manera fresca y original. Su amiga y colega Hermann Weyl describió su producción académica en tres épocas:
Producción científica de Emmy Noether cayó en tres épocas claramente diferenciadas:(1) el período de dependencia relativa, 1907-1919;
(3) el estudio de la álgebras no conmutativa, sus representaciones de transformaciones lineales, y su aplicación al estudio de los campos de número conmutativos y sus aritmética.
(2) las investigaciones agrupadas en torno a la teoría general de los ideales 1920-1926;-Weyl 1935
En la primera época (1907-1919), Noether se ocupa principalmente de diferenciales y algebraicas invariantes, a partir de su tesis bajo Paul Gordan. Sus horizontes matemáticos ampliaron, y su trabajo se hizo más general y abstracto, como ella se familiarizó con la obra de David Hilbert , a través de una estrecha interacción con el sucesor de Gordan, Ernst Fischer Segismundo. Después de mudarse a Göttingen en 1915, produjo su obra fundamental para la física, los dos Teoremas de Noether.
En la segunda época (1920-1926), Noether se dedicó a desarrollar la teoría de la anillos matemáticos.
En la tercera época (1927-1935), Noether se centró en álgebra no conmutativa, transformaciones lineales, y los campos de número conmutativa.
Contexto histórico
En el siglo de 1832 a la muerte de Noether en 1935, el campo de las matemáticas, específicamente álgebra -underwent una revolución profunda, cuyos ecos aún se sienten. Los matemáticos de los siglos anteriores habían trabajado en métodos prácticos para resolver determinados tipos de ecuaciones, por ejemplo, cúbico, cuarto grado, y ecuaciones de quinto grado, así como en el problema relacionado de construir polígonos regulares con regla y compás . Comenzando con Carl Friedrich Gauss 1832 prueba 's que los números primos , como puede ser de cinco factor in Enteros de Gauss, Introducción de Evariste Galois de grupos de permutaciones en 1832 (aunque, a causa de su muerte, sus trabajos fueron publicados sólo en 1846 por Liouville), El descubrimiento de William Rowan Hamilton de cuaterniones en 1843, y Definición más moderna de Arthur Cayley de grupos en 1854, la investigación se dirigió a la determinación de las propiedades de los sistemas cada vez más abstractos definidos por las normas cada vez más universales. Las contribuciones más importantes de Noether a las matemáticas eran para el desarrollo de este nuevo campo, el álgebra abstracta .
Resumen álgebra y begriffliche Mathematik (matemática conceptual)
Dos de los objetos más básicos en álgebra abstracta son grupos y anillos.
Un grupo consiste en un conjunto de elementos y una sola operación que combina un primer y un segundo elemento y devuelve un tercio. La operación debe satisfacer ciertas restricciones para que se determine un grupo: Debe ser cerrado (cuando se aplica a cualquier par de elementos del conjunto asociado, el elemento generado también debe ser un miembro de ese grupo), debe ser asociativa , debe haber ser un elemento de identidad (un elemento que, cuando se combina con otro elemento utilizando la operación, los resultados en el elemento original, como la adición de cero a un número o multiplicándolo por uno), y por cada elemento debe haber una elemento inverso.
Un anillo de la misma manera, tiene un conjunto de elementos, pero ahora tiene dos operaciones. La primera operación se debe hacer el conjunto de un grupo, y la segunda operación es asociativa y distributiva con respecto a la primera operación. Se puede o no puede ser conmutativa ; esto significa que el resultado de aplicar la operación a un primero y un segundo elemento es el mismo que para la segunda y primera-el orden de los elementos, no importa. Si cada elemento distinto de cero tiene un inverso multiplicativo (un elemento x tal que ax = xa = 1), el anillo se llama un anillo de división. La campo se define como un anillo de división conmutativo.
Los grupos se estudiaron con frecuencia a través de representaciones de grupo . En su forma más general, estos consisten en una selección de grupo, un conjunto y una acción del grupo en el set, es decir, una operación que toma un elemento del grupo y un elemento del conjunto y devuelve un elemento de el conjunto. Muy a menudo, el conjunto es un espacio vectorial , y el grupo representa simetrías del espacio vectorial. Por ejemplo, hay un grupo que representa las rotaciones rígidas de espacio. Este es un tipo de simetría del espacio, porque el espacio en sí no cambia cuando se gira a pesar de que las posiciones de los objetos en que lo hacen. Noether utiliza este tipo de simetrías en su trabajo sobre los invariantes de la física.
Una forma poderosa de estudiar anillos es a través de sus módulos . Un módulo se compone de una selección de anillo, otro conjunto, por lo general distinta del conjunto subyacente del ring y llama el conjunto subyacente del módulo, una operación sobre pares de elementos del conjunto subyacente del módulo, y una operación que toma un elemento del anillo y un elemento del módulo y devuelve un elemento del módulo. El conjunto subyacente del módulo y su funcionamiento debe formar un grupo. Un módulo es una versión junta teórica de una representación del grupo: Haciendo caso omiso de la segunda operación de anillo y la operación en pares de elementos del módulo determina una representación del grupo. La verdadera utilidad de los módulos es que los tipos de módulos que existen y sus interacciones, revelan la estructura del anillo en formas que no son evidentes a partir de la propia anillo. Un caso especial importante de esto es un álgebra . (La palabra álgebra significa tanto un sujeto dentro de las matemáticas, así como un objeto estudiado en el tema de álgebra.) Un álgebra consiste en una selección de dos anillos y una operación que toma un elemento de cada anillo y devuelve un elemento del segundo anillo . Esta operación hace que el segundo anillo en un módulo sobre el primero. A menudo, el primer anillo es un campo.
Palabras como "elemento" y "la combinación de la operación" son muy generales, y se puede aplicar a muchas situaciones del mundo real y abstractas. Cualquier conjunto de cosas que obedece todas las reglas para una (o dos) operación (s) es, por definición, un grupo (o anillo), y obedece a todos los teoremas sobre grupos (o anillos). Números enteros y las operaciones de suma y multiplicación, son sólo un ejemplo. Por ejemplo, los elementos podrían ser las palabras de datos de computadoras, donde la operación combinando primero es exclusivo o, y la segunda es conjunción lógica. Los teoremas de álgebra abstracta son poderosos porque son generales; gobiernan muchos sistemas. Se podría imaginar que poco se podía llegar a la conclusión acerca de los objetos definidos con tan pocas propiedades, sino precisamente en ella yacía regalo de Noether: descubrir el máximo que podría concluirse de un determinado conjunto de propiedades, o por el contrario, para identificar el conjunto mínimo, lo esencial propiedades responsables de una observación particular . A diferencia de la mayoría de los matemáticos, ella no hizo abstracciones generalizando a partir de ejemplos conocidos; más bien, trabajó directamente con las abstracciones. Como van der Waerden recordó en su obituario de ella,
La máxima de que Emmy Noether fue guiado a través de su trabajo podría formularse de la siguiente manera: "Las relaciones entre los números, funciones y operaciones se vuelven transparentes, de aplicación general, y totalmente productiva sólo después de que se han aislado de sus objetos particulares y han formulado como conceptos universalmente válidos.
Este es el begriffliche Mathematik (matemática puramente conceptual) que era característico de Noether. Este estilo de las matemáticas fue adoptado por otros matemáticos y, después de su muerte, floreció en nuevas formas, tales como la teoría de categorías.
Los enteros como un ejemplo de un anillo
Los enteros forman un anillo conmutativo cuyos elementos son los números enteros, y las operaciones que combinan son la suma y la multiplicación. Cualquier par de enteros puede ser añadido o multiplica , siempre resulta en otro entero, y la primera operación, además, es conmutativa , es decir, para cualquier elementos a y b en el ring, un + b = b + a . La segunda operación, multiplicación, también es conmutativa, pero eso no es necesariamente cierto para otros anillos, lo que significa que un combinado con b podría ser diferente de b combinado con una . Los ejemplos de anillos no conmutativos incluyen matrices y cuaterniones. los números enteros no forman un anillo de división, debido a que la segunda operación no puede siempre ser invertida; no hay número entero un tal que 3 × un = 1.
Los enteros tienen propiedades adicionales que no generalizan a todos los anillos conmutativos. Un ejemplo importante es el teorema fundamental de la aritmética , que dice que todo entero positivo puede ser un factor de forma única en números primos . Factorizaciones únicos no siempre existen en otros anillos, pero Noether encontraron un teorema de factorización única, que ahora se llama el teorema de Lasker-Noether , por los ideales de muchos anillos. Gran parte del trabajo de Noether laicos en la determinación de qué propiedades no son válidas para todos los anillos, en la elaboración de nuevos análogos de los viejos teoremas enteros, y para determinar el conjunto mínimo de suposiciones necesarias para obtener ciertas propiedades de los anillos.
Primera época (1908-1919)
Algebraica teoría de invariantes

Gran parte del trabajo de Noether en la primera época de su carrera se asoció con la teoría de invariantes, principalmente la teoría de invariantes algebraicos. La teoría de invariantes se refiere a las expresiones que se mantienen constantes (invariantes) bajo un grupo de transformaciones. Como un ejemplo cotidiano, si un criterio rígido se gira, las coordenadas ( x , y , z ) de sus puntos finales cambia, pero su longitud L dada por la fórmula L 2 = Δ x 2 + Δ y 2 Δ + z 2 sigue siendo el mismo. La teoría de invariantes era un área activa de investigación en el siglo XIX después, impulsados en parte por Felix Klein programa de Erlangen, según la cual los diferentes tipos de geometría deben ser caracterizadas por sus invariantes bajo transformaciones, por ejemplo, la cruz-relación de la geometría proyectiva. La arquetípica ejemplo de un invariante es el discriminante B 2 - 4 de CA de una forma binaria cuadrática Ax 2 + Bxy + Cy 2 . Esto se llama un invariante porque no se ha modificado mediante sustituciones lineales x → ax + por , y → cx + dy con determinante ad - bc = 1. Estas sustituciones forman el grupo especial lineal SL 2 . (No hay invariantes en el marco del grupo lineal general de todas las transformaciones lineales invertibles porque estas transformaciones se pueden multiplicar por un factor de escala. Para remediar esta teoría, clásica invariante también considerado invariantes relativas , que eran formas invariante hasta un factor de escala). Una pueden solicitar todos los polinomios en A , B , y C , que son sin cambios por la acción de SL 2 ; éstos se llaman los invariantes de formas cuadráticas binarias, y resultan ser los polinomios en el discriminante. De manera más general, se puede pedir a los invariantes de polinomios homogéneos A 0 x r Y 0 + ... + A r x 0 Y r de mayor grado, que serán determinadas polinomios en los coeficientes A 0 , ..., A r , y más en general aún, se puede hacer la pregunta similar para polinomios homogéneos en más de dos variables.
Uno de los objetivos principales de la teoría de invariantes era para resolver el "problema de base finita". La suma o producto de dos invariantes es invariante, y el problema de base finita preguntaron si era posible obtener todos los invariantes comenzando con una lista finita de invariantes, llamados generadores , y luego, añadiendo o multiplicando los generadores juntos. Por ejemplo, el discriminante da una base finita (con un elemento) para los invariantes de las formas cuadráticas binarias. Asesor de Noether, Paul Gordan, era conocido como el "rey de la teoría de invariantes", y su principal contribución a las matemáticas fue su solución 1870 del problema base finita de invariantes de polinomios homogéneos en dos variables. Él demostró esto dando un método constructivo para encontrar todos los invariantes y sus generadores, pero no fue capaz de llevar a cabo este enfoque constructivo para invariantes en tres o más variables. En 1890, David Hilbert demostró una declaración similar para los invariantes de polinomios homogéneos en cualquier número de variables. Además, su método funcionó, no sólo para el grupo lineal especial, pero también para algunos de sus subgrupos tales como el grupo ortogonal especial. Su primera prueba causó una cierta controversia, ya que no dio un método para construir los generadores, aunque en el trabajo más tarde hizo su método constructivo. Para su tesis, Noether amplió prueba computacional de Gordan de polinomios homogéneos en tres variables. Enfoque constructivo de Noether hizo posible el estudio de las relaciones entre los invariantes. Más tarde, después de que ella se había convertido en métodos más abstractos, Noether llamó a su tesis Mist (basura) y Formelngestrüpp (una jungla de ecuaciones).
La teoría de Galois
La teoría de Galois refiere transformaciones de los campos de número que permutar las raíces de una ecuación. Consideremos una ecuación polinómica de una variable x de grado n , en el que los coeficientes se han extraído de alguna campo suelo, que podrían ser, por ejemplo, el campo de los números reales , números racionales , o los números enteros modulo 7. Puede o no puede haber opciones de x , que hacen que este polinomio evaluar a cero. Tales opciones, si existen, se denominan raíces. Si el polinomio es x 2 + 1 y el campo es los números reales, entonces el polinomio no tiene raíces, porque cualquier elección de x hace que el polinomio mayor que o igual a uno. Si el campo se extiende, sin embargo, entonces el polinomio puede ganar raíces, y si se ha extendido lo suficiente, entonces siempre tiene un número de raíces igual a su grado. Continuando con el ejemplo anterior, si el campo se amplía a los números complejos, entonces las ganancias polinómicas dos raíces, i y - i , donde i es la unidad imaginaria , es decir, i 2 = -1 . Más generalmente, el campo de extensión en el que un polinomio puede tenerse en cuenta en sus raíces se conoce como el campo de la división del polinomio.
La Grupo de Galois de un polinomio es el conjunto de todas las formas de transformar el cuerpo de descomposición, preservando al mismo tiempo el campo de tierra y las raíces del polinomio. (En la jerga matemática, estas transformaciones se denominan automorfismos.) El grupo de Galois de x 2 + 1 consta de dos elementos: La transformación de identidad, que envía cada número complejo a sí mismo, y la conjugación compleja, que envía i a - i . Desde el grupo de Galois no cambia el campo de tierra, deja los coeficientes del polinomio sin cambios, por lo que debe dejar el conjunto de todas las raíces sin cambios. Cada raíz puede moverse a otro raíz, sin embargo, por lo que la transformación determina una permutación de los n raíces entre sí. La importancia del grupo de Galois deriva del teorema fundamental de la teoría de Galois, lo que demuestra que los campos que se encuentran entre el campo de tierra y el cuerpo de descomposición están en correspondencia uno a uno con los subgrupos del grupo de Galois.
En 1918, Noether publicó un artículo seminal sobre el problema inverso de Galois. En lugar de determinar el grupo de Galois de las transformaciones de un campo determinado y su extensión, Noether se le preguntó si, habida cuenta de un campo y un grupo, siempre es posible encontrar una extensión del campo que tiene el grupo que recibió como su grupo de Galois. Ella redujo esto a " un problema de Noether ", que se pregunta si el campo fijo de un subgrupo G del grupo de la permutación S n que actúa sobre el campo k ( x 1 , ..., x n ) siempre es una pura extensión trascendental del campo k . (Se menciona por primera vez este problema en un documento de 1913, en la que atribuyó el problema a su colega Fischer.) Ella demostró que esto era cierto para n = 2 , 3 ó 4. En 1969, RG Cisne encontró un contraejemplo al problema de Noether , con n = 47 y G un grupo cíclico de orden 47 (aunque este grupo puede ser realizado como un grupo de Galois sobre los números racionales de otras maneras). El problema inverso de Galois sigue sin resolverse.
Física
Noether fue llevado a Göttingen en 1915 por David Hilbert y Felix Klein, que quería que su experiencia en la teoría de invariantes para ayudarles en la comprensión de la relatividad general , la teoría geométrica de la gravitación desarrollada principalmente por Albert Einstein . Hilbert había observado que la conservación de la energía parecía ser violada en la relatividad general, debido al hecho de que la energía gravitacional podría gravitar en sí. Noether proporciona la resolución de esta paradoja, y una herramienta fundamental de la moderna física teórica, con primer teorema de Noether, que se demostró en 1915, pero no publicó hasta 1918. Ella resolvió el problema no sólo para la relatividad general, pero determinó las cantidades conservadas para cada sistema de leyes físicas que posee cierta simetría continua.
Sobre la recepción de su trabajo, Einstein escribió a Hilbert:. "Ayer me recibió de la señorita Noether un artículo muy interesante sobre invariantes Estoy impresionado de que tales cosas pueden ser entendidas de una manera tan general La vieja guardia en Gotinga debería tomar algunas lecciones de. ! La señorita Noether Ella parece saber sus cosas ".
Por ejemplo, si un sistema físico se comporta de la misma, independientemente de la forma en que se orienta en el espacio, las leyes físicas que gobiernan son rotacionalmente simétrica; de esta simetría, el teorema de Noether muestra el momento angular del sistema debe ser conservada. El sistema físico en sí no necesita ser simétrica; un asteroide dentado de volteo en el espacio conserva el momento angular a pesar de su asimetría. Más bien, la simetría de las leyes físicas que rigen el sistema es responsable de la ley de conservación. Como otro ejemplo, si un experimento de física tiene el mismo resultado en cualquier lugar y en cualquier momento, sus leyes son simétricas bajo traducciones continuas en el espacio y el tiempo; por el teorema de Noether, estas simetrías representan las leyes de conservación de cantidad de movimiento y energía dentro de este sistema, respectivamente.
El teorema de Noether se ha convertido en una herramienta fundamental de la moderna física teórica, tanto por la visión que da a las leyes de conservación, y también, como una herramienta de cálculo práctico. Su teorema permite a los investigadores para determinar las cantidades conservadas de las simetrías observadas de un sistema físico. Por el contrario, facilita la descripción de un sistema físico basado en clases de leyes físicas hipotéticas. Por ejemplo, supongamos que un nuevo fenómeno físico se descubre. El teorema de Noether ofrece una prueba para los modelos teóricos del fenómeno: si la teoría tiene una simetría continua, entonces el teorema de Noether garantiza que la teoría tiene una cantidad conservada, y para la teoría es correcta, esta conservación debe ser observable en los experimentos.
Segunda época (1920-1926)
Aunque los resultados de la primera época de Noether fueron impresionantes y útil, su fama como matemático se basa más en el trabajo pionero que hizo en su segunda y tercera épocas, como se ha señalado por Hermann Weyl y BL van der Waerden en sus obituarios de ella.
En estas épocas, no se limitó a aplicar las ideas y métodos de matemáticos anteriores; más bien, que estaba elaborando nuevos sistemas de definiciones matemáticas que serían utilizadas por los matemáticos futuros. En particular, desarrolló una nueva teoría de ideales en anillos, generalizando el trabajo anterior de Richard Dedekind. Ella también es conocida por el desarrollo ascendente condiciones en cadena, una condición finitud simple que arrojó resultados poderosos en sus manos. Tales condiciones y la teoría de los ideales permitieron Noether generalizar muchos resultados mayores y para tratar viejos problemas desde una nueva perspectiva, como la teoría de la eliminación y las variedades algebraicas que habían sido estudiados por su padre.
Ascendiendo y descendiendo condiciones cadena
En esta época, Noether se hizo famoso por su hábil uso de ascender (Teilerkettensatz) o descendente (Vielfachenkettensatz) condiciones en cadena. Una secuencia de no vacíossubconjuntos A 1,A 2,A 3, etc. de unconjunto Spor lo general se dice que esascendente, si cada uno es un subconjunto de la siguiente
Por el contrario, una secuencia de subconjuntos deSse llamadescendentesi cada uno contiene la siguiente subconjunto:
Una cadena se vuelve constante después de un número finito de pasos si hay un n tal que 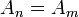 para todo m ≥ n . Una colección de subconjuntos de un conjunto dado satisface la condición de cadena ascendente si cualquier secuencia ascendente se vuelve constante después de un número finito de pasos. Se satisface la condición de cadena descendente si cualquier secuencia descendente se vuelve constante después de un número finito de pasos.
para todo m ≥ n . Una colección de subconjuntos de un conjunto dado satisface la condición de cadena ascendente si cualquier secuencia ascendente se vuelve constante después de un número finito de pasos. Se satisface la condición de cadena descendente si cualquier secuencia descendente se vuelve constante después de un número finito de pasos.
Condiciones Ascendente y de la cadena descendente son generales, lo que significa que se pueden aplicar a muchos tipos de objetos matemáticos y, en la superficie, es posible que no parecen muy potente. Noether mostró cómo explotar esas condiciones, sin embargo, a la máxima ventaja: por ejemplo, cómo los utilizan para mostrar que todo conjunto de sub-objetos tiene un máximo / mínimo o elemento de que un objeto complejo puede ser generada por un menor número de elementos . Estas conclusiones menudo son pasos cruciales en una prueba.
Existen muchos tipos de objetos en álgebra abstracta puede satisfacer las condiciones de la cadena, y por lo general si satisfacen una condición de cadena ascendente, están llamados Noetheriano en su honor. , por definición, un anillo noetheriano satisface una condición de cadena ascendente en sus ideales de izquierda y derecha, mientras que un grupo noetheriano se define como un grupo en el que cada cadena estrictamente ascendente de subgrupos es finito. La módulo noetheriano es un módulo en el que toda cadena estrictamente ascendente de submódulos se rompe después de un número finito. La espacio noetheriano es un espacio topológico en el que toda cadena estrictamente creciente de subespacios abiertos rompe después de un número finito de términos; esta definición se hace para que el espectro de un anillo noetheriano es un espacio topológico noetheriano.
La condición de la cadena es a menudo "heredada" por sub-objetos. Por ejemplo, todos los subespacios de un espacio noetheriano, son Noetherian sí mismos; todos los subgrupos y grupos cociente de un grupo noetheriano son igualmente, noetheriano, y, mutatis mutandis , lo mismo vale para submódulos y módulos del cociente de un módulo noetheriano. Todos los anillos cociente de un anillo noetheriano son noetheriano, pero que no necesariamente tienen por sus subanillos. La condición de la cadena también puede ser heredado por combinaciones o extensiones de un objeto noetheriano. Por ejemplo, las sumas directas finitos de anillos noetherianos son noetheriano, como es el anillo de formal de series de potencias sobre un anillo noetheriano.
Otra aplicación de tales condiciones de la cadena está en noetheriano inducción también conocido como inducción que fundados es una generalización de la inducción matemática. Con frecuencia se usa para reducir declaraciones generales sobre colecciones de objetos a las declaraciones sobre objetos específicos en esa colección. Supongamos que S es un conjunto parcialmente ordenado. Una forma de probar una declaración acerca de los objetos de S es asumir la existencia de un contraejemplo y deducir una contradicción, lo que demuestra la contraposición de la declaración original. La premisa básica de la inducción Noetherian es que cada subconjunto no vacío de S contiene un elemento mínimo. En particular, el conjunto de todos los contraejemplos contiene un elemento mínimo, el contraejemplo mínimo . Con el fin de probar la declaración original, por lo tanto, es suficiente probar algo aparentemente mucho más débil: Para cualquier contraejemplo, hay un contraejemplo más pequeño.
Conmutativos anillos, ideales, y módulos
Papel de Noether, Idealtheorie en Ringbereichen ( Teoría de ideales en Anillo Dominios , 1921), es el fundamento de la teoría general anillo conmutativo, y da una de las primeras definiciones generales de un anillo conmutativo . Antes de su papel, la mayoría de los resultados en álgebra conmutativa se restringieron a los ejemplos especiales de los anillos conmutativos, tales como anillos de polinomios sobre los campos o anillos de enteros algebraicos. Noether demostró que en un anillo que satisface la condición de cadena ascendente de ideales, todo ideal es de generación finita. En 1943, el matemático francés Claude Chevalley acuñó el término, anillo noetheriano , para describir esta propiedad. Un resultado importante en el papel de Noether 1921 es el teorema de Lasker-Noether , que se extiende el teorema de Lasker en la descomposición primaria de los ideales de anillos de polinomios a todos los anillos noetherianos. El teorema de Lasker-Noether se puede ver como una generalización del teorema fundamental de la aritmética que establece que cualquier entero positivo se puede expresar como un producto de números primos , y que esta descomposición es única.
De Noether trabajo Abstrakter Aufbau der Idealtheorie en algebraischen Zahl- und Funktionenkörpern ( Estructura abstracta de la teoría de ideales en algebraica Número y Función Campos , 1927) caracteriza los anillos en el que los ideales tienen factorización única en ideales primos como los dominios de Dedekind: dominios integrales que son noetheriano, 0 o 1- dimensional y integralmente cerrado en sus campos de cociente. Este documento también contiene lo que ahora se llama los teoremas de isomorfismo, que describen algunos fundamentales isomorfismos naturales, y algunos otros resultados básicos sobre noetherianos y módulos Artinian.
Teoría Eliminación
En 1923-1924, Noether aplica su teoría ideal para la eliminación teoría en una formulación que ella atribuye a su alumna, Kurt Hentzelt-mostrando que los teoremas fundamentales sobre la factorización de polinomios podría ser prorrogados directamente. Tradicionalmente, teoría de la eliminación se refiere a la eliminación de uno o más variables de un sistema de ecuaciones polinómicas, por lo general por el método de resultantes. Para ilustración, el sistema de ecuaciones a menudo se puede escribir en la forma de una matriz M (falta la variable x ) veces un vector v (que tiene sólo diferentes potencias de x ) igualando el vector cero, M • v = 0 . Por lo tanto, el determinante de la matriz M debe ser cero, proporcionando una nueva ecuación en la que la variable x se ha eliminado.
La teoría de invariantes de grupos finitos
Técnicas como la solución no constructiva original de Hilbert al problema base finita no podían utilizarse para obtener información cuantitativa sobre los invariantes de una acción de grupo, y además, no se aplican a todas las acciones de grupo. En su documento de 1915, Noether encontró una solución al problema de base finita para un grupo finito de transformaciones G actúa sobre un espacio vectorial de dimensión finita sobre un campo de característica cero. Su solución muestra que el anillo de invariantes es generado por invariantes homogéneos cuyo grado es menor que, o igual a, el orden del grupo finito; esto se llama, Noether de cota . Su papel le dio dos pruebas de Noether de encuadernados, los cuales también funcionan cuando la característica del campo es coprimero a | G | !, el factorial de la orden | G | del grupo G . El número de generadores no tendrá que cumplir más de Noether límite cuando la característica del campo divide el | G |, pero Noether no fue capaz de determinar si el obligado era correcta cuando la característica del campo divide | G |! pero no | G |. Durante muchos años, la determinación de la verdad o falsedad de la cota en este caso fue un problema abierto llamada "brecha de Noether". Finalmente, se resolvió de forma independiente por Fleischmann en 2000 y Fogarty en 2001, que ambos mostraron que el límite sigue siendo cierto.
En su documento de 1926, extendió el teorema de Noether Hilbert a las representaciones de un grupo finito sobre cualquier campo; el nuevo caso de que no se desprende de la obra de Hilbert, es cuando la característica del campo divide el orden del grupo. Resultado de Noether se extendió más tarde por William Haboush a todos los grupos reductivos por su demostración de la conjetura de Mumford. En este trabajo Noether también introdujo el Noether normalización lema , lo que demuestra que un tipo finito de dominio Un sobre un campo k tiene un conjunto x 1 , ..., x n de elementos algebraicamente independientes tales que A es integral sobre k [ x 1 , ..., x n ] .
Las contribuciones a la topología
Como ha señalado Pavel Alexandrov y Hermann Weyl en sus obituarios, las contribuciones de Noether a Topología ilustrar su generosidad con las ideas y cómo sus ideas podrían transformar campos enteros de matemáticas. En topología, los matemáticos estudian las propiedades de los objetos que permanecen invariantes incluso bajo deformación, propiedades tales como su conectividad. Una broma común es que un topólogo no puede distinguir un donut de una taza de café, ya que pueden deformarse continuamente entre sí.
Noether se acredita con las ideas fundamentales que llevaron al desarrollo de la topología algebraica de la anterior topología combinatoria, en concreto, la idea de grupos de homología. De acuerdo con el relato de Alexandrov, Noether asistió a conferencias impartidas por Heinz Hopf y él en los veranos de 1926 y 1927, donde "ella continuamente hizo observaciones, que a menudo eran profunda y sutil", y continúa diciendo que,
Cuando ... ella primero se familiarizó con una construcción sistemática de la topología combinatoria, ella inmediatamente observó que valdría la pena estudiar directamente los grupos de complejos algebraicas y los ciclos de un poliedro dado y el subgrupo del grupo de ciclo que consta de ciclos homólogos a cero; en lugar de la definición usual de números de Betti, sugirió definir inmediatamente el grupo Betti como (cociente) grupo complementario del grupo de todos los ciclos por el subgrupo de ciclos homólogos a cero. Esta observación parece ahora evidente. Pero en aquellos años (1925- 28 ) se trataba de un nuevo punto de vista.
La sugerencia de que la topología Noether estudiarse algebraicamente, fue adoptado inmediatamente por Hopf, Alexandrov, y los demás, y se convirtió en un tema frecuente de debate entre los matemáticos de Göttingen. Noether observó que su idea de un grupo de Betti hace que la fórmula de Euler-Poincaré más fácil de entender, y el propio trabajo de Hopf sobre este tema "lleva la impronta de estos comentarios de Emmy Noether". Noether menciona sus propias ideas de topología sólo como un aparte en una publicación 1926, donde ella lo cita como una aplicación de la teoría de grupos .
El enfoque algebraico a la topología se desarrolló independientemente en Austria . En un curso 1926-27 dada en Viena , Leopold Vietoris definió un grupo de homología, que fue desarrollado por Walther Mayer, en una definición axiomática en 1928.

Tercera época (1927-1935)
Números hipercomplejos y teoría de la representación
Gran parte del trabajo sobre los números hipercomplejos y representaciones de grupo se llevó a cabo en los siglos XIX y XX, pero seguía siendo dispares. Noether unido los resultados y dio la primera teoría de la representación general de los grupos y álgebras. En pocas palabras, Noether subsumido la teoría estructura del álgebras asociativas y la teoría de la representación de los grupos en una única teoría aritmética de módulos y los ideales en los anillos que cumplan las condiciones de la cadena ascendente. Esta sola obra por Noether era de importancia fundamental para el desarrollo del álgebra moderna.
Álgebra no conmutativa
Noether también fue responsable de una serie de otros avances en el campo del álgebra. Con Emil Artin,Richard Brauer, yHelmut Hasse, fundó la teoría deálgebras simples centrales.
Un papel seminal de Noether, Helmut Hasse y Richard Brauer pertenece a álgebras de división, que son sistemas algebraicos en el que la división es posible. Probaron dos teoremas importantes: un teorema local mundial afirmando que si un álgebra central de dimensión finita división en un campo de número divide a nivel local en todas partes y luego se divide a nivel mundial (así es trivial), ya partir de esto, deducida su Hauptsatz ("teorema principal") : cada dimensión finita central de álgebra de división sobre un número algebraico campo F divide sobre una extensión ciclotómico cíclica . Estos teoremas permiten clasificar todas las álgebras de división central de dimensión finita sobre un campo determinado número. Un documento posterior de Noether mostró, como un caso especial de un teorema más general, que todos los subcampos máximas de una división álgebra D son campos de división. Este documento también contiene el teorema de Skolem-Noether que establece que cualquiera de las dos inmersiones de una extensión de un campo k en un álgebra sencilla dimensión finita central sobre k , son conjugados. La Brauer-Noether teorema da una caracterización de los campos de división de una división central álgebra sobre un campo.
Evaluación, reconocimiento y memoriales

El trabajo de Noether sigue siendo relevante para el desarrollo de la física teórica y las matemáticas y ella está considerado como uno de los más grandes matemáticos del siglo XX. En su obituario, compañero algebrista BL van der Waerden dice que su originalidad matemática era "absoluta sin comparación", y Hermann Weyl dijo que Noether "cambió la faz de álgebra por su trabajo ". Durante su vida, e incluso hasta hoy, Noether se ha caracterizado como el más grande matemático de la mujer en la historia escrita por los matemáticos como Pavel Alexandrov, Hermann Weyl, y Jean Dieudonné.
En una carta a The New York Times,Albert Einsteinescribió:
En el juicio de los matemáticos que viven más competentes, Fräulein Noether fue la matemática creativa más significativa genio hasta ahora producido desde el inicio de la educación superior de las mujeres. En el ámbito del álgebra, en la que los matemáticos más talentosos han estado ocupados durante siglos, descubrió los métodos que han demostrado ser de enorme importancia en el desarrollo de la actual generación más joven de los matemáticos.
El 2 de enero de 1935, pocos meses antes de su muerte, el matemáticoNorbert Wiener escribió que
Señorita Noether es ... el mayor matemático mujer que ha vivido; y el más grande científico de la mujer de cualquier tipo que ahora vive, y un estudioso, al menos en el plano de Madame Curie .
En una exposición en el 1964Feria Mundial dedicado alos matemáticos modernos, Noether fue la única mujer representados entre los matemáticos notables del mundo moderno.
Noether ha sido galardonado en varios monumentos conmemorativos,
- La Asociación para la Mujer en Matemáticas tiene una Conferencia Noether para honrar a las mujeres en matemáticas cada año; en su folleto de 2005 para el evento, la Asociación caracteriza Noether como "uno de los grandes matemáticos de su tiempo, alguien que trabajó y luchó por lo que ella amaba y creía. Su vida y su obra siguen siendo una tremenda fuente de inspiración".
- En consonancia con su dedicación a sus estudiantes, laUniversidad de Siegen alberga sus matemáticas y departamentos de física en los edificios enel Campus Emmy Noether.
- La Fundación Alemana de Investigación (Deutsche Forschungsgemeinschaft) opera elPrograma de Noether Emmy, una beca de proporcionar financiación a prometedores jóvenes investigadores post-doctorales en sus nuevas actividades de investigación y docencia.
- Una calle en su ciudad natal, Erlangen, ha sido nombrado después de Emmy Noether y su padre, Max Noether.
- El sucesor de la escuela secundaria asistió en Erlangen ha sido renombrado comola Escuela de Noether Emmy.
En la ficción, Emmy Nutter, el profesor de física en "La patente de Dios" por Ransom Stephens, se basa en los Emmy Noether
Más lejos de casa,
- El cráter Tro en ellado lejano de la Luna lleva su nombre.
- La 7001 Noether asteroide también lleva el nombre de Emmy Noether.
Lista de los estudiantes de doctorado
| Fecha | Nombre del estudiante | Título de la tesis y la traducción Inglés | Universidad | Publicación | |
|---|---|---|---|---|---|
| 16/12/1911 | Falckenberg, Hans | Verzweigungen von Lösungen nichtlinearer Differentialgleichungen
| Erlangen | Leipzig 1912 | |
| 04/03/1916 | Seidelmann, Fritz | Muere Gesamtheit der kubischen und biquadratischen Gleichungen mit Affekt bei beliebigem Rationalitätsbereich
| Erlangen | Erlangen 1916 | |
| 02/25/1925 | Hermann, Grete | Die Frage der endlich vielen Schritte in der Theorie der Polynomideale unter Benutzung nachgelassener Sätze von Kurt Hentzelt
| Göttingen | Berlín 1926 | |
| 07/14/1926 | Grell, Heinrich | Beziehungen zwischen den Idealen verschiedener Ringe
| Göttingen | Berlín 1927 | |
| 1927 | Dorate, Wilhelm | Über einem verallgemeinerten Gruppenbegriff
| Göttingen | Berlín 1927 | |
| murió antes de defensa | Holzer, Rudolf | Zur Theorie der Ringe primären
| Göttingen | Berlín 1927 | |
| 06/12/1929 | Weber, Werner | Idealtheoretische Deutung der Darstellbarkeit beliebiger natürlicher Zahlen durch Quadratische Formen
| Göttingen | Berlín 1930 | |
| 26/06/1929 | Levitski, Jakob | Reduzible vollständig Über Ringe und Unterringe
| Göttingen | Berlín 1931 | |
| 18/06/1930 | Deuring, Max | Zur Theorie der arithmetischen algebraischen Funktionen
| Göttingen | Berlín 1932 | |
| 29/07/1931 | Montaje, Hans | Zur Theorie der Automorphismenringe Abelscher Gruppen und ihr Analogon bei nichtkommutativen Gruppen
| Göttingen | Berlín 1933 | |
| 07/27/1933 | Witt, Ernst | Riemann-Rochscher Satz und Zeta-Funktion im Hyperkomplexen
| Göttingen | Berlín 1934 | |
| 12/06/1933 | Tsen, Chiungtze | Algebren über Funktionenkörpern
| Göttingen | Göttingen 1934 | |
| 1934 | Schilling, Otto | Über gewisse Beziehungen der zwischen Arithmetik hyperkomplexer Zahlsysteme und algebraischer Zahlkörper
| Marburg | Braunschweig 1935 | |
| 1935 | Stauffer, Ruth | La construcción de una base normal en un campo de extensión separable | Bryn Mawr | Baltimore 1936 | |
| 1935 | Vorbeck, Werner | Nichtgaloissche Zerfällungskörper einfacher Systeme
| Göttingen | ||
| 1936 | Wichmann, Wolfgang | Anwendungen der p-adischen Theorie im Nichtkommutativen
| Göttingen | Monatshefte für Mathematik und Physik(1936)44, 203-24. |
Temas matemáticos epónimos
|
|
|