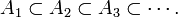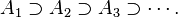Emmy Noether
Contexte des écoles Wikipédia
Enfants SOS offrent un chargement complet de la sélection pour les écoles pour une utilisation sur les intranets des écoles. Parrainage d'enfants aide les enfants du monde en développement à apprendre aussi.
| Emmy Noether | |
|---|---|
 | |
| Né | Amalie Emmy Noether 23 Mars 1882 Erlangen, Bavière, Allemagne |
| Mort | 14 Avril 1935 (53 ans) Bryn Mawr, en Pennsylvanie, États-Unis |
| Nationalité | Allemand |
| Les champs | Mathématiques et physique |
| Institutions | Université de Göttingen Bryn Mawr College |
| Alma mater | Université d'Erlangen |
| Conseiller de doctorat | Paul Gordan |
| Doctorants | Max Deuring Hans Fitting Grete Hermann Chiungtze Tsen Jacob Levitzki Otto Schilling Ernst Witt |
| Connu pour | Algèbre abstraite Physique théorique |
Emmy Noether (allemand: [Nøːtɐ]; nom officiel Amalie Emmy Noether, le 23 Mars 1882 au 14 Avril 1935), était un influent Allemand mathématicien connu pour ses contributions révolutionnaires à l'algèbre abstraite et la physique théorique. Décrit par Pavel Alexandrov, Albert Einstein , Jean Dieudonné, Hermann Weyl, Norbert Wiener et d'autres comme la femme la plus importante dans l'histoire des mathématiques, elle a révolutionné les théories de bagues, champs, et algèbres. En physique, Théorème de Noether explique le lien fondamental entre symétrie et lois de conservation.
Elle est née dans une famille juive dans la Ville bavaroise de Erlangen; son père était mathématicien Max Noether. Emmy initialement prévu pour enseigner le français et l'anglais après avoir passé les examens requis, mais a étudié les mathématiques à la Université d'Erlangen, où son père a enseigné. Après avoir terminé sa thèse en 1907 sous la supervision de Paul Gordan, elle a travaillé à l'Institut de mathématiques de Erlangen sans salaire pendant sept ans (à l'époque les femmes ont été largement exclues des postes universitaires). En 1915, elle a été invitée par David Hilbert et Felix Klein pour rejoindre le département de mathématiques à la Université de Göttingen, un centre de renommée mondiale de la recherche mathématique. La faculté de philosophie opposé, cependant, et elle a passé quatre ans des conférences sous le nom de Hilbert. Son habilitation a été approuvé en 1919, lui permettant d'obtenir le grade de Privatdozent.
Noether est resté un des principaux membres de la Göttingen département de mathématiques jusqu'en 1933; ses élèves étaient parfois appelés les "garçons" Noether. En 1924, le mathématicien néerlandais BL van der Waerden rejoint son cercle et est rapidement devenu le leader expositor des idées de Noether: son travail était la fondation pour le second volume de son influence 1931 manuel, Moderne Algebra. Au moment de son Adresse plénière à la 1932 Congrès international des mathématiciens à Zürich , son sens algébrique a été reconnu dans le monde entier. L'année suivante, le gouvernement de l'Allemagne nazie rejeté Juifs de postes universitaires et Noether déménagé aux États-Unis de prendre une position à Bryn Mawr College en Pennsylvanie. En 1935, elle a subi une chirurgie pour un kyste de l'ovaire et, malgré des signes de reprise, est mort quatre jours plus tard à l'âge de 53.
Travail mathématique de Noether a été divisée en trois «époques». Dans la première (1908- 19 ), elle a fait d'importantes contributions à la théorie de invariants algébriques et les champs numériques. Son travail sur les invariants différentiels dans le calcul des variations , Théorème de Noether, a été appelé «l'un des théorèmes mathématiques les plus importants jamais révélés dans l'orientation du développement de la physique moderne». Dans la deuxième époque (1920- 26 ), elle a commencé à travailler que «changé le visage de [résumé] l'algèbre". Dans son article classique Idealtheorie dans Ringbereichen (Théorie des idéaux dans la bague Domaines, 1921) Noether développé la théorie de idéaux dans les anneaux commutatifs dans un outil puissant avec des applications de grande envergure. Elle a fait usage élégant de la Conditions de chaîne, et le satisfaire objets sont nommés Noethérien en son honneur. Dans la troisième époque (1927- 35 ), elle a publié d'importants travaux sur algèbres non commutatives et numéros hypercomplexes et unis le théorie des représentations des groupes avec la théorie de modules et des idéaux. En plus de ses propres publications, Noether était généreux avec ses idées et est crédité de plusieurs axes de recherche publiés par d'autres mathématiciens, même dans des domaines très éloignés de son travail principal, comme topologie algébrique.
Biographie

Le père de Emmy, Max Noether, était issu d'une famille de commerçants de gros en Allemagne. Il avait été paralysé par la poliomyélite à l'âge de quatorze ans. Il a retrouvé la mobilité, mais une jambe est restée affectée. En grande partie autodidacte, il a reçu une doctorat de la Université de Heidelberg en 1868. Après avoir enseigné pendant sept ans, il a pris une position dans la ville bavaroise de Erlangen, où il a rencontré et épousé Ida Amalia Kaufmann, la fille d'un marchand prospère. Contributions mathématiques de Max Noether devaient géométrie algébrique principalement, en suivant les traces de Alfred Clebsch. Ses meilleurs résultats connus sont le Brill-Noether théorème et le résidu, ou Théorème AF + BG; plusieurs autres théorèmes sont associés avec lui, y compris Le théorème de Max Noether.
Emmy Noether est né le 23 Mars 1882, la première de quatre enfants. Son premier nom était "Amalie", après que sa mère et grand-mère paternelle, mais elle a commencé à utiliser son deuxième prénom à un jeune âge. Comme une fille, elle a été très apprécié. Elle ne se distingue pas bien académiquement elle était connue pour être intelligent et convivial. Emmy était myope et a parlé avec un mineur Lisp pendant l'enfance. Un ami de la famille a raconté une histoire ans plus tard à propos de Young Emmy résoudre rapidement un casse-tête à la fête pour enfants, montrant un sens aigu logiques à cet âge précoce. Emmy a appris à cuisiner et nettoyer, comme la plupart des filles de l'époque, et elle a pris des leçons de piano. Elle a poursuivi aucun de ces activités avec passion, même si elle aimait danser.
Elle avait trois frères plus jeunes. L'aîné, Alfred, est né en 1883, a obtenu un doctorat en chimie de Erlangen en 1909, mais il est mort neuf ans plus tard. Fritz Noether, né en 1884, est connu pour ses réalisations académiques: après des études à Munich il a fait une réputation pour lui-même en mathématiques appliquées . Le plus jeune, Gustav Robert, est né en 1889. On sait très peu sur sa vie; il souffrait d'une maladie chronique et mourut en 1928.
Université d'Erlangen

Emmy Noether a montré la maîtrise précoce en français et en anglais. Au printemps 1900, elle a passé l'examen pour les enseignants de ces langues et a reçu une note globale de sehr gut (très bien). Sa performance lui qualifié pour enseigner les langues dans les écoles réservées aux filles, mais elle a plutôt choisi de poursuivre ses études à la Université d'Erlangen.
Ce était une décision non conventionnelle; deux ans plus tôt, le Sénat académique de l'université a déclaré que permettre enseignement mixte serait "renverser tout ordre académique». Une des deux seules femmes étudiants dans une université de la 986, Noether n'a été autorisé à classes d'audit plutôt que de participer pleinement, et doivent l'autorisation individuelle des professeurs dont les conférences qu'elle souhaitait y assister. Malgré les obstacles, le 14 Juillet 1903, elle a réussi l'examen de fin d'études à un Realgymnasium dans Nuremberg.
Pendant le semestre d'hiver 1903-1904, elle a étudié à l'Université de Göttingen, assister à des conférences données par l'astronome Karl Schwarzschild et mathématiciens Hermann Minkowski, Otto Blumenthal, Felix Klein et David Hilbert . Peu de temps après, les restrictions à la participation des femmes dans cette université ont été annulées.
Noether retourné à Erlangen. Elle rentra officiellement l'université le 24 Octobre 1904, et a déclaré son intention de se concentrer uniquement sur les mathématiques. Sous la supervision du Paul Gordan elle a écrit sa thèse, Über die Bildung des Formensystems der ternären biquadratischen formulaire (sur des systèmes complets d'invariants pour les formulaires ternaire biquadratiques, 1907). Bien qu'il ait été bien reçu, Noether décrit plus tard sa thèse que "la merde".
Pour les sept prochaines années (1908- 15 ), elle a enseigné à l'Université de l'Institut mathématique de Erlangen sans salaire, parfois substituer à son père quand il était trop malade pour donner des conférences. En 1910 et 1911, elle a publié une extension de son travail de thèse à partir de trois variables à n variables.

Gordan retraite au printemps de 1910, mais a continué à enseigner occasionnellement avec son successeur, Erhard Schmidt, qui a quitté peu après pour un poste dans Breslau. Gordan retiré de l'enseignement tout à fait en 1911 avec l'arrivée du successeur de Schmidt Ernst Fischer, et mort en Décembre 1912.
Selon Hermann Weyl, Fischer était une influence importante sur Noether, en particulier par son introduction à l'œuvre de David Hilbert . De 1913 à 1916 Noether publié plusieurs articles se étendant et en appliquant les méthodes de Hilbert à des objets mathématiques tels que domaines de fonctions rationnelles et la invariants de groupes finis. Cette phase marque le début de son engagement avec l'algèbre abstraite , le domaine des mathématiques à laquelle elle aurait faire des contributions révolutionnaires.
Noether et Fischer partagent la jouissance animé de mathématiques et seraient souvent discuter conférences longtemps après qu'ils étaient plus; Noether est connu pour avoir envoyé des cartes postales à Fischer continue son train de pensées mathématiques.
Université de Göttingen
Au printemps de 1915, Noether a été invité à retourner à l'université de Göttingen par David Hilbert et Felix Klein. Leur effort pour la recruter, cependant, a été bloqué par le philologues et historiens entre la faculté philosophique: les femmes, ils ont insisté, ne doit pas devenir Privatdozent. Un membre du corps professoral a protesté: «Que vont penser nos soldats quand ils retournent à l'université et trouvent qu'ils sont tenus d'apprendre aux pieds d'une femme?" Hilbert a répondu avec indignation, déclarant: «Je ne vois pas que le sexe du candidat est un argument contre son admission comme Privatdozent. Après tout, nous sommes une université, pas une maison de bain."

Noether parti pour Göttingen à la fin Avril; deux semaines plus tard sa mère est décédé subitement à Erlangen. Elle avait déjà reçu des soins médicaux pour une maladie oculaire, mais sa nature et de l'impact sur son décès est inconnue. A la même époque, le père de Noether retraite et son frère a rejoint le Armée allemande à servir dans la Première Guerre mondiale . Elle est revenue à Erlangen pendant plusieurs semaines, la plupart du temps pour se occuper de son père vieillissant.
Au cours de ses premières années d'enseignement à Göttingen elle ne avait pas une position officielle et n'a pas été payée; sa famille a payé pour sa chambre et pension et soutenu son travail académique. Ses conférences ont été souvent annoncés sous le nom de Hilbert, et Noether fourniraient «assistance».
Peu après son arrivée à Göttingen, cependant, elle a démontré ses capacités en prouvant le théorème maintenant connu comme Le théorème de Noether, qui montre qu'un loi de conservation est associé à aucun différentiable symétrie d'un système physique. Physiciens américains Leon Lederman et Christopher T. Hill soutiennent dans leur livre Symétrie et Belle Univers que le théorème de Noether est "certainement l'un des théorèmes mathématiques les plus importants jamais révélés dans l'orientation du développement de la physique moderne, peut-être sur un pied d'égalité avec le théorème de Pythagore ".

Lorsque la Première Guerre mondiale terminée, le Révolution allemande de 1918 à 1919 a apporté un changement important dans les attitudes sociales, y compris plus de droits pour les femmes. En 1919, l'Université de Göttingen a permis Noether de procéder avec elle habilitation (admissibilité à la permanence). Son examen oral a eu lieu à la fin mai, et elle a livré avec succès son habilitation conférence en Juin.
Trois ans plus tard, elle a reçu une lettre de la Ministre de Prusse pour la science, l'art, et de l'éducation publique, dans laquelle il lui a conféré le titre de professeur nicht beamteter ausserordentlicher (professeur non titulaires de droits d'administration internes limitées et fonctions). Ce était un professeur non rémunéré «extraordinaire», et non plus la chaire «ordinaire», qui était un poste à la fonction publique. Même se il a reconnu l'importance de son travail, la position encore fourni aucun salaire. Noether n'a pas été payée pour ses conférences jusqu'à ce qu'elle a été nommé à la situation particulière des Lehrbeauftragte für Algèbre un an plus tard.
Travail séminal dans l'algèbre abstraite
Bien que le théorème de Noether a eu un effet profond sur la physique, parmi les mathématiciens, elle est surtout connu pour ses contributions séminales à l'algèbre abstraite . Comme Nathan Jacobson dit dans son introduction aux Collected Papers de Noether,
Le développement de l'algèbre abstraite, qui est l'une des innovations les plus distinctifs de mathématiques du XXe siècle, est en grande partie en raison de son - dans les documents publiés, des conférences, et influence personnelle sur ses contemporains.
Le travail de pionnier de Noether en algèbre a commencé en 1920. En collaboration avec W. Schmeidler, elle a ensuite publié un document sur le théorie des idéaux dans lesquels ils définis idéaux à gauche et droite dans un anneau. L'année suivante, elle a publié un document historique appelé Idealtheorie dans Ringbereichen, analyse croissant conditions de la chaîne à l'égard des idéaux (mathématiques). Algébriste noté Irving Kaplansky appelé ce travail «révolutionnaire»; la publication a donné lieu à l'expression " Anneau noethérien ", et plusieurs autres objets mathématiques appelés Noethérien.
En 1924, un jeune mathématicien néerlandais, BL van der Waerden, est arrivé à l'Université de Göttingen. Il a immédiatement commencé à travailler avec Noether, qui a fourni de précieuses méthodes de conceptualisation abstraite. van der Waerden a dit plus tard que son originalité était "absolue sans comparaison". En 1931, il a publié Moderne Algèbre, un texte central dans le domaine; son second volume beaucoup emprunté le travail de Noether. Bien Emmy Noether ne cherche pas la reconnaissance, il a inclus dans une note dans la septième édition "basé en partie sur des conférences données par E. Artin et E. Noether ". Elle a permis parfois ses collègues et étudiants de recevoir un crédit pour ses idées, les aidant à développer leur carrière au détriment de sa propre.
La visite de van der Waerden faisait partie d'une convergence des mathématiciens de partout dans le monde à Göttingen, qui est devenu un pôle majeur de la recherche mathématique et physique. De 1926 à 1930 Russie topologist Pavel Alexandrov a enseigné à l'université, et lui et Noether est rapidement devenu de bons amis. Il a commencé à se référant à elle comme der Noether, en utilisant l'article allemand masculin comme un terme d'affection pour montrer son respect. Elle a essayé d'organiser pour lui d'obtenir un poste à Göttingen comme professeur régulier, mais n'a pu l'aider à sécuriser une bourse de la Fondation Rockefeller. Ils se sont rencontrés régulièrement et ont apprécié les discussions sur les intersections de l'algèbre et de la topologie. Dans son adresse mémoire 1935, Alexandrov nommé Emmy Noether "le plus grand mathématicien femme de tous les temps".
Lecturing et les étudiants
À Göttingen, Noether supervisé plus d'une douzaine de doctorants; elle a été la première Grete Hermann, qui a défendu sa thèse en Février 1925. Elle a parlé plus tard avec respect de son «thèse-mère" .. Noether a également supervisé Max Deuring, qui se est distingué comme un cycle et a continué à contribuer de manière significative au domaine de la la géométrie arithmétique; Hans montage, connu pour Montage de théorème et de la Lemme de Fitting; et Chiungtze Tsen (également rendu "Chiungtze C. Tsen" en anglais), qui a prouvé Le théorème de Tsen. Elle a également travaillé en étroite collaboration avec Wolfgang Krull, qui a fait avancer algèbre commutative avec son Hauptidealsatz et son la théorie de la dimension pour anneaux commutatifs.
En plus de sa perspicacité mathématique, Noether a été respectée pour sa considération pour les autres. Bien que parfois elle a agi brutalement envers ceux qui étaient en désaccord avec elle, elle a néanmoins gagné une réputation pour la serviabilité constante et des conseils aux patients de nouveaux étudiants. Sa loyauté envers précision mathématique causé une collègue de nommer son «un critique sévère», mais elle a combiné cette demande de précision avec une attitude nourricière. Un collègue l'a décrite plus tard, de cette façon: "Complètement unegotistical et sans vanité, elle n'a jamais prétendu rien pour elle-même, mais la promotion des œuvres de ses élèves avant tout."
Son style de vie frugal était d'abord due à la rémunération étant refusé pour son travail; Toutefois, même après l'université a commencé à lui verser un petit salaire en 1923, elle a continué à vivre une vie simple et modeste. Elle a été payé plus généreusement plus tard dans sa vie, mais la moitié de son salaire sauvé de léguer à son neveu, Gottfried E. Noether.
Partiellement indifférents sur l'apparence et les manières, elle se est concentrée sur ses études à l'exclusion de la romance et de la mode. Un algébriste distingués Olga Taussky-Todd décrit un déjeuner, au cours de laquelle Noether, entièrement plongé dans une discussion des mathématiques, "gesticulait sauvagement», comme elle mangeait et "renversé sa nourriture constamment et essuya de sa robe, complètement imperturbable". étudiants d'apparence soucieux grincé des dents, comme elle a récupéré le mouchoir de sa blouse et ignoré le désarroi croissant de ses cheveux lors d'une conférence. Deux étudiantes se sont approchés une fois lors d'une pause dans une classe de deux heures pour exprimer leur inquiétude, mais ils ont été incapables de percer la discussion des mathématiques énergique qu'elle avait avec d'autres étudiants.
Selon la notice nécrologique de van der Waerden des Emmy Noether, elle n'a pas suivi un plan de leçon pour ses conférences, qui a frustré certains étudiants. Au lieu de cela, elle a utilisé ses conférences comme un temps de discussion spontanée avec ses élèves, à réfléchir et clarifier importants problèmes de pointe en mathématiques. Certains de ses résultats les plus importants ont été développés dans ces conférences, et les notes de cours de ses élèves ont formé la base de plusieurs manuels importants, tels que ceux de van der Waerden et Deuring.
Plusieurs de ses collègues ont assisté à ses conférences, et elle permis à certains de ses idées, comme le produit croisé (verschränktes Produkt en allemand) des algèbres associatives, qui sera publié par d'autres. Noether a été enregistré comme ayant donné au moins cinq cours d'un semestre à Göttingen:
- Hiver 1924-1925: Gruppentheorie und hyperkomplexe Zahlen (Théorie Groupe et hypercomplexes Numbers)
- Hiver 1927-1928: Hyperkomplexe Grössen und Darstellungstheorie (Quantités hypercomplexes et Théorie des représentations)
- Été 1928: Nichtkommutative Algebra (Algèbre non commutative)
- Été 1929: Nichtkommutative Arithmetik (non-commutative arithmétique)
- Hiver 1929-1930: Algèbre der hyperkomplexen Grössen (Algèbre des quantités hypercomplexes).
Ces cours souvent précédées principales publications dans ces domaines.
Noether parlait rapidement, reflétant la vitesse de ses pensées, beaucoup ont dit et ont exigé une grande concentration de ses étudiants. Les étudiants qui ne aimaient pas son style souvent sentir aliéné. Certains élèves ont estimé qu'elle dépendait trop discussions spontanées. Ses élèves les plus dévoués, cependant, ont savouré l'enthousiasme avec lequel elle se approcha de mathématiques, d'autant plus que ses conférences souvent construites sur des travaux antérieurs qu'ils avaient fait ensemble.
Elle a développé un cercle étroit de collègues et d'étudiants qui pensaient le long des lignes similaires et avaient tendance à exclure ceux qui ne l'ont pas. «outsiders» qui, occasionnellement, visité les conférences de Noether dépensent habituellement seulement 30 minutes dans la salle avant de partir dans la frustration ou de la confusion. Un étudiant régulier dit d'une telle instance: "L'ennemi a été vaincu, il a autorisé à sortir."
Noether a montré une dévotion à son sujet et ses élèves qui se étendaient au-delà de la journée scolaire. Une fois, lorsque le bâtiment a été fermé pour des vacances de l'État, elle a réuni la classe sur les marches à l'extérieur, les conduisit à travers les bois, et a enseigné à un café local. Plus tard, après qu'elle avait été rejetée par le Troisième Reich , elle a invité les étudiants à son domicile pour discuter de leurs plans futurs et les concepts mathématiques.
Moscou

Dans l'hiver de 1928-1929 Noether accepté une invitation à L'Université de Moscou, où elle a continué à travailler avec PS Alexandrov. En plus d'exercer avec ses recherches, elle a donné des cours en algèbre abstraite et géométrie algébrique. Elle a travaillé avec les topologues, Lev Pontriaguine et Nikolai Chebotaryov, qui plus tard a salué ses contributions au développement de la théorie de Galois .
Bien que la politique ne était pas au centre de sa vie, Noether a pris un vif intérêt pour les questions politiques et, selon Alexandrov, a montré un soutien considérable pour la révolution russe (1917) . Elle était particulièrement heureux de voir soviétiques progrès dans les domaines de la science et des mathématiques, qu'elle jugeait indicatif de nouvelles opportunités rendues possibles par la Projet bolchevique. Cette attitude lui a causé des problèmes en Allemagne, culminant dans son éviction d'une bâtiment d'hébergement de pension, après que les dirigeants étudiants plaint de vivre avec «une juive marxiste-penchant".

Noether prévu de retourner à Moscou, un effort pour lequel elle a reçu le soutien de Alexandrov. Après avoir quitté l'Allemagne en 1933, il a essayé de l'aider à acquérir une chaire à l'Université d'Etat de Moscou par la Soviétique ministère de l'Education. Bien que cet effort se est avéré infructueux, ils correspondaient fréquemment pendant les années 1930, et en 1935 elle a fait des plans pour un retour à l'Union soviétique. Pendant ce temps son frère, Fritz a accepté un poste à l'Institut de recherche pour les mathématiques et la mécanique dans Tomsk, dans le district fédéral de Sibérie de la Russie, après avoir perdu son emploi en Allemagne.
Reconnaissance
En 1932, Emmy Noether et Emil Artin a reçu le Prix commémoratif Ackermann-Teubner pour leurs contributions aux mathématiques. Le prix réalisé une récompense monétaire de 500 Reichsmarks et a été vu comme une reconnaissance officielle, attendue depuis longtemps de son travail considérable dans le domaine. Néanmoins, ses collègues ont exprimé leur frustration devant le fait qu'elle n'a pas été élu à la Göttingen Gesellschaft der Wissenschaften (Académie des sciences) et n'a jamais été promu au poste de professeur Ordentlicher (professeur titulaire).

Les collègues de Noether a célébré son cinquantième anniversaire en 1932, dans le style de mathématiciens typiques. Helmut Hasse a consacré un article à elle dans le Mathematische Annalen, dans laquelle il lui a confirmé le soupçon que certains aspects de algèbre non commutative sont plus simples que celles de algèbre commutative, en prouvant une non commutative la loi de réciprocité. Ce lui plaisait énormément. Il lui a également envoyé une énigme mathématique, la «mμν-énigme de syllabes", dont elle résolu immédiatement; l'énigme a été perdu.
En Novembre de la même année, Noether a prononcé une allocution plénière (großer de Vortrag) sur "les systèmes Hyper-complexes dans leurs relations d'algèbre commutative et de la théorie des nombres" à la Congrès international des mathématiciens à Zürich . Le congrès a réuni 800 personnes, y compris les collègues de Noether Hermann Weyl, Edmund Landau, et Wolfgang Krull. Il y avait 420 participants officiels et vingt-et-un adresses plénières présentées. Apparemment, la position de parole éminent de Noether était une reconnaissance de l'importance de ses contributions aux mathématiques. Le congrès 1932 est parfois décrit comme le point de sa carrière.
Expulsion de Göttingen
Lorsque Adolf Hitler est devenu le Reichskanzler allemand en Janvier 1933, les nazis l'activité dans le pays a augmenté de façon spectaculaire. À l'Université de Göttingen l'Association allemande des étudiants a mené l'attaque sur «l'esprit de non-allemande" attribué aux Juifs et a été aidé par un Privatdozent nommé Werner Weber, ancien élève de Emmy Noether. Attitudes antisémites ont créé un climat hostile aux professeurs juifs. Un jeune manifestant aurait demandé: «aryens étudiants veulent les mathématiques et les mathématiques aryennes pas juifs."
Une des premières actions de l'administration d'Hitler était le Loi pour la restauration de la fonction publique professionnelle qui a supprimé les Juifs et les employés du gouvernement politiquement suspects (y compris les professeurs d'université) de leur emploi à moins qu'ils avaient «démontré leur loyauté à l'Allemagne" en servant dans la Première Guerre mondiale En Avril 1933 Noether reçu un avis de ministère prussien des sciences, les arts et l'éducation publique qui se lisait: "Sur la base de l'alinéa 3 du Code de la fonction publique du 7 Avril 1933, je retire par les présentes de vous le droit d'enseigner à l'Université de Göttingen." Plusieurs des collègues de Noether, y compris Max Born et Richard Courant, a également eu leurs positions révoqués. Noether a accepté la décision calmement, fournir un soutien pour les autres pendant cette période difficile. Hermann Weyl a écrit plus tard que «Emmy Noether-son courage, sa franchise, son insouciance de son propre destin, son esprit de conciliation-était au milieu de toute la haine et la bassesse, le désespoir et le chagrin qui nous entoure, un réconfort moral." Typiquement, Noether est resté concentré sur les mathématiques, la collecte des étudiants dans son appartement pour discuter la théorie du corps de classes. Lorsque l'un de ses élèves est apparu dans l'uniforme de l'organisation paramilitaire nazie Sturmabteilung (SA), elle ne montrait aucun signe d'agitation et, paraît-il, a même ri à ce sujet plus tard.
Bryn Mawr

Comme des dizaines de professeurs nouveaux chômeurs ont commencé à chercher des postes en dehors de l'Allemagne, leurs collègues aux États-Unis ont cherché à fournir une assistance et des possibilités d'emploi pour eux. Albert Einstein et Hermann Weyl ont été nommés par le Institute for Advanced Study de Princeton, tandis que d'autres ont travaillé pour trouver un sponsor requis pour juridique immigration. Noether a été contacté par les représentants des deux établissements d'enseignement, Bryn Mawr College aux États-Unis et Somerville College de l' Université d'Oxford en Angleterre. Après une série de négociations avec le Fondation Rockefeller, une subvention pour Bryn Mawr a été approuvé pour Noether et elle a pris une position là-bas, à partir de fin 1933.
Au Bryn Mawr, Noether a rencontré et lié d'amitié Anna Wheeler, qui avait étudié à Göttingen juste avant Noether est arrivé là. Une autre source de soutien au collège était le président Bryn Mawr, Marion Edwards Park, qui a invité enthousiasme mathématiciens dans la région de «voir le Dr Noether en action!" Noether et une petite équipe d'étudiants ont travaillé rapidement par van der Moderne 1930 livre Algèbre I de Waerden et des parties de Theorie der algebraischen de Erich Hecke Zahlen (Théorie des nombres algébriques, 1908).
En 1934, a commencé Noether cours à l'Institute for Advanced Study à Princeton, à l'invitation du Abraham Flexner et Oswald Veblen. Elle a également travaillé avec et supervisé Abraham Albert et Harry Vandiver. Toutefois, elle a fait remarquer à propos de l'Université de Princeton qu'elle ne était pas la bienvenue au «université des hommes, où rien ne est admis femme".
Son temps aux États-Unis était agréable, entourée comme elle l'était par des collègues de soutien et absorbée dans ses sujets de prédilection. À l'été 1934, elle retourne brièvement en Allemagne pour voir Emil Artin et son frère Fritz avant son départ pour Tomsk. Bien que beaucoup de ses anciens collègues avaient été forcés de quitter les universités, elle a pu utiliser la bibliothèque comme un «chercheur étranger».
Mort

En Avril 1935 les médecins ont découvert une tumeur dans de Noether bassin. Inquiet de complications de la chirurgie, ils ont ordonné à deux jours de repos au lit en premier. Au cours de l'opération, ils ont découvert une kyste de l'ovaire "de la taille d'un gros cantaloup ". Deux petites tumeurs dans son utérus semblait être bénignes et ne ont pas été retiré, pour éviter de prolonger la chirurgie. Pendant trois jours, elle est apparue en convalescence normalement, et elle a récupéré rapidement à partir d'un collapsus circulatoire sur le quatrième. Le 14 Avril, elle tomba inconscient, sa température a grimpé à 109 ° F (42,8 ° C), et elle est morte. "[I] l ne est pas facile de dire ce qui se était passé dans Dr Noether", l'un des médecins a écrit. "Il est possible qu'il y ait une certaine forme d'infection rare et virulente, qui a frappé la base du cerveau où les centres de chaleur sont censés être situé."
Quelques jours après la mort de Noether ses amis et associés à Bryn Mawr lieu un petit service commémoratif à la maison de président du Collège Park. Hermann Weyl et Richard Brauer a voyagé de Princeton et a parlé avec Wheeler et Taussky de leur collègue disparu. Dans les mois qui ont suivi, hommages écrits ont commencé à apparaître dans le monde entier: Albert Einstein a rejoint van der Waerden, Weyl, et Pavel Alexandrov à payer leurs égards. Son corps a été incinéré et les cendres enterré sous la passerelle autour des cloîtres de la Martha Thomas Bibliothèque au Bryn Mawr.
Contributions aux mathématiques et à la physique
Tout d'abord Noether est rappelé par les mathématiciens comme un algébriste et pour son travail dans la topologie . Les physiciens apprécient son mieux pour elle fameux théorème raison de ses conséquences de grande portée pour physique théorique et systèmes dynamiques. Elle a montré une propension aiguë à la pensée abstraite, qui lui a permis d'aborder des problèmes de mathématiques d'une manière fraîche et originale. Son ami et collègue Hermann Weyl décrit sa production savante en trois époques:
La production scientifique de Emmy Noether tombé dans trois époques bien distinctes:(1) la période de dépendance relative, de 1907 à 1919;
(3) l'étude de la algèbres non-commutative, leurs représentations par des transformations linéaires, et leur application à l'étude des champs de numéro commutatives et leurs arithmétique.
(2) les enquêtes regroupées autour de la théorie générale des idéaux de 1920 à 1926;-Weyl 1935
Dans la première époque (1907-1919), a porté principalement sur Noether invariants différentiels et algébriques, à commencer par sa thèse sous Paul Gordan. Ses horizons élargis mathématiques, et son travail est devenu plus générale et abstraite, comme elle fait la connaissance de l'œuvre de David Hilbert , par des interactions étroites avec un successeur à Gordan, Ernst Sigismund Fischer. Après avoir déménagé à Göttingen en 1915, elle a produit son ouvrage précurseur pour la physique, les deux Les théorèmes de Noether.
Dans la deuxième époque (1920-1926), Noether se consacre au développement de la théorie de anneaux mathématiques.
Dans la troisième époque (1927-1935), axé sur Noether algèbre non commutative, transformations linéaires, et les champs numériques commutatives.
Contexte historique
Au cours du siècle de 1832 à la mort de Noether en 1935, le domaine des mathématiques spécifiquement algèbre -underwent une profonde révolution, dont les répercussions se font encore sentir. Mathématiciens des siècles précédents avaient travaillé sur les méthodes pratiques pour résoudre certains types d'équations, par exemple, cubique, quartique, et quintiques équations, ainsi que sur la problème connexe de la construction polygones réguliers utilisant règle et au compas . Commençant par Carl Friedrich Gauss 1832 la preuve de ce que les nombres premiers tels que cinq peut être pris en compte Entiers de Gauss, L'introduction de Évariste Galois de groupes de permutation en 1832 (même si, en raison de sa mort, ses papiers ne ont été publiés en 1846 par Liouville), La découverte de William Rowan Hamilton quaternions en 1843, et Définition plus moderne d'Arthur Cayley de groupes en 1854, la recherche se est tourné vers la détermination des propriétés des systèmes toujours plus abstraites définies par des règles toujours plus universelles. Contributions les plus importantes de Noether aux mathématiques étaient au développement de ce nouveau champ, algèbre abstraite .
Résumé algèbre et begriffliche Mathematik (de mathématiques conceptuelle)
Deux des la plupart des objets de base de l'algèbre abstraite sont des groupes et des anneaux.
Un groupe est constitué d'un ensemble d'éléments et une seule opération qui combine un premier et un deuxième élément et renvoie un tiers. L'opération doit satisfaire à certaines contraintes pour elle de déterminer un groupe: Il doit être fermé (lorsqu'il est appliqué à toute paire d'éléments de l'ensemble associé, l'élément généré doit également être un membre de cet ensemble), il doit être associative , il faut être un élément d'identité (d'un élément qui, lorsqu'il est combiné avec un autre élément à l'aide de l'opération, se traduit par l'élément d'origine, comme l'ajout d'un certain nombre zéro ou le multipliant par une), et pour chaque élément il doit y avoir un élément inverse.
Un anneau de même, dispose d'un ensemble d'éléments, mais il a maintenant deux opérations. La première opération doit faire l'ensemble d'un groupe, et la deuxième opération est associative et distributive par rapport à la première opération. Il peut ou peut ne pas être commutative ; cela signifie que le résultat de l'application de l'opération à un premier et un deuxième élément est la même que pour la deuxième et la première ordre des éléments n'a pas d'importance. Si chaque élément non nul a un inverse multiplicatif (un élément x que cette hache = xa = 1), l'anneau est appelé un anneau de division. Un champ est défini comme un anneau de division commutative.
Les groupes sont souvent étudiés à travers des représentations du groupe . Dans leur forme la plus générale, ceux-ci se composent d'un choix du groupe, un ensemble, et une l'action du groupe sur l'ensemble, qui est, une opération qui prend un élément du groupe et un élément de l'ensemble et renvoie un élément de l'ensemble. Le plus souvent, l'ensemble est un espace vectoriel , et le groupe représente les symétries de l'espace vectoriel. Par exemple, il est un groupe qui représente les rotations rigides de l'espace. Ceci est un type de symétrie de l'espace, parce que l'espace lui-même ne change pas quand il est tourné, même si les positions des objets qu'il font. Noether utilisé ces sortes de symétries dans son travail sur les invariants de la physique.
Ceci est la begriffliche Mathematik (mathématiques purement conceptuel) qui était caractéristique de Noether. Ce style de mathématiques a été adopté par d'autres mathématiciens et, après sa mort, a fleuri dans de nouvelles formes, telles que théorie des catégories.
Entiers comme un exemple d'une bague
Les entiers forment un anneau commutatif dont les éléments sont les entiers, et les opérations sont combinant addition et la multiplication. Toute paire de nombres entiers peut être ajouté ou multiplié , toujours dans le cadre d'un entier, et la première opération, plus, est commutatif , ie, pour tout éléments a et b dans le ring, un + b = b + a . La seconde opération, la multiplication, est aussi commutative, mais cela ne doit pas être vrai pour d'autres cycles, ce qui signifie que d'un combiné avec b pourrait être différente de b combiné avec un . Des exemples de noyaux non commutatives comprennent matrices et quaternions. Les entiers ne forment pas un anneau de division, parce que la deuxième opération ne peut pas toujours être inversée; il n'y a pas de nombre entier d'une telle sorte que 3 × a = 1.
Les entiers ont des propriétés supplémentaires qui ne généralisent pas à tous les anneaux commutatifs. Un exemple important est le théorème fondamental de l'arithmétique , qui dit que chaque entier positif peut être prise en compte unique en nombres premiers . Factorisations uniques existent pas toujours dans d'autres anneaux, mais Noether trouvé un théorème de factorisation unique maintenant appelé le théorème Lasker-Noether , pour les idéaux de nombreux anneaux. Une grande partie du travail de Noether résidait dans la détermination de ce que les propriétés ne sont valables pour tous les anneaux, à l'élaboration de nouveaux analogues de l'ancien théorèmes entiers, et dans la détermination de l'ensemble minimal d'hypothèses requises pour obtenir certaines propriétés des anneaux.
Première époque (1908-1919)
Algébrique théorie des invariants

Une grande partie du travail de Noether dans la première époque de sa carrière a été associée à la théorie des invariants, principalement la théorie des invariants algébrique. La théorie des invariants concerne expressions qui restent constants (invariant) en vertu d'un groupe de transformations. A titre d'exemple tous les jours, si un critère rigide est mis en rotation, les coordonnées ( x , y , z ) de ses extrémités changer, mais sa longueur L donnée par la formule L 2 = Δ x 2 + Δ y 2 + Δ z 2 est la même. La théorie des invariants était un domaine de recherche actif à la fin du XIXe siècle, en partie inspirée par Felix Klein programme Erlangen, selon laquelle les différents types de géométrie doivent être caractérisés par leurs invariants sous les transformations, par exemple, le contre-rapport de la géométrie projective. Le archétype exemple d'un invariant est le discriminant B 2 - 4 AC d'une forme quadratique binaire Ax 2 + Bxy + Cy 2 . Ceci est appelé un invariant, car il est inchangé par des substitutions linéaires x → ax + par , y → cx + dy de déterminant ad - bc = 1. Ces substitutions constituent le groupe spécial linéaire SL 2 . (Il n'y a pas invariants dans le cadre du groupe linéaire général sur les transformations linéaires inversibles parce que ces transformations peuvent être multiplication par un facteur d'échelle. Pour remédier à cela, la théorie des invariants classique également examiné invariants relatifs , qui étaient des formes invariantes jusqu'à un facteur d'échelle.) Une peut demander tous les polynômes dans A , B et C qui sont inchangés par l'action de SL 2 ; ceux-ci sont appelés les invariants de formes quadratiques binaires, et se révèlent être les polynômes dans le discriminant. Plus généralement, on peut se poser pour les invariants de polynômes homogènes A 0 x r y 0 + ... + A r x 0 y r de degré supérieur, qui seront certains polynômes en les coefficients A 0 , ..., A r , et plus généralement encore, on peut poser la même question pour les polynômes homogènes dans plus de deux variables.
L'un des principaux objectifs de la théorie des invariants était de résoudre le «problème de base finie". La somme ou d'un produit de deux des invariants est invariant, et le problème de base finie demandé si il était possible d'obtenir tous les invariants en commençant par une liste finie d'invariants, appelé générateurs , puis, en ajoutant ou en multipliant les générateurs ensemble. Par exemple, le discriminant donne une base finie (avec un élément) pour les invariants de formes quadratiques binaires. Le conseiller de Noether, Paul Gordan, était connu comme le "roi de la théorie des invariants", et sa principale contribution aux mathématiques était sa solution 1870 du problème de base finie pour les invariants de polynômes homogènes à deux variables. Il l'a prouvé en donnant une méthode constructive pour trouver tous les invariants et leurs générateurs, mais n'a pas été en mesure de mener à bien cette approche constructive des invariants dans trois ou plusieurs variables. En 1890, David Hilbert a prouvé une déclaration similaire pour les invariants de polynômes homogènes dans un certain nombre de variables. En outre, sa méthode a fonctionné, non seulement pour le groupe spécial linéaire, mais aussi pour certains de ses sous-groupes tels que le groupe spécial orthogonal. Sa première preuve causé une certaine controverse, car il ne donne pas une méthode pour construire les générateurs, bien que dans le travail plus tard, il a fait sa méthode constructive. Pour sa thèse, Noether étendu preuve de calcul de Gordan aux polynômes homogènes dans trois variables. L'approche constructive de Noether a permis d'étudier les relations entre les invariants. Plus tard, après qu'elle eut tourné vers des méthodes plus abstraites, Noether appelé sa thèse Mist (merde) et Formelngestrüpp (une jungle d'équations).
La théorie de Galois
La théorie de Galois concerne les transformations des champs numériques qui permutent les racines d'une équation. Considérons une équation polynomiale d'une variable x de degré n , dans laquelle les coefficients sont tirées de certains corps de base, ce qui pourrait être, par exemple, le domaine des nombres réels , des nombres rationnels , ou les entiers modulo 7. Il peut ou peut ne pas être des choix de x , qui font de ce polynôme évaluer à zéro. Ces choix, si elles existent, sont appelés racines. Si le polynôme est x 2 + 1 et le champ est les nombres réels, alors le polynôme n'a pas de racines, parce que tout choix de x rend le polynôme supérieur ou égal à un. Si le champ est étendu, cependant, alors le polynôme peut avoir des racines, et si elle est prolongée assez, alors il a toujours un certain nombre de racines égales à son degré. En reprenant l'exemple précédent, si le champ est élargi pour les nombres complexes, puis les gains polynômes deux racines, i et - i , où i est l' unité imaginaire , qui est, i 2 = -1 . Plus généralement, la zone d'extension dans lequel un polynôme peut être pris en compte dans ses racines est connu comme le domaine du polynôme de division.
Le Groupe de Galois d'un polynôme est l'ensemble de tous les moyens de transformation de la matière de séparation, tout en préservant la zone de sol et les racines du polynôme. (Dans le jargon mathématique, ces transformations sont appelés automorphismes.) Le groupe de Galois de x 2 + 1 se compose de deux éléments: La transformation de l'identité, qui envoie chaque nombre complexe en lui-même, et la conjugaison complexe, qui envoie i à - i . Depuis le groupe de Galois ne change pas le champ de terre, il laisse les coefficients du polynôme inchangée, de sorte qu'il doit quitter l'ensemble des racines inchangés. Chaque racine peut se déplacer à une autre racine, cependant, si la transformation détermine une permutation des n racines entre eux. L'importance du groupe de Galois dérive du théorème fondamental de la théorie de Galois, ce qui prouve que les champs se trouvant entre le champ de terre et le champ de fractionnement sont en correspondance un-à-un avec les sous-groupes du groupe de Galois.
En 1918, Noether a publié un document fondamental sur le problème inverse de Galois. Au lieu de déterminer le groupe de Galois de transformations d'un domaine donné et son extension, Noether demandé si, compte tenu d'un champ et d'un groupe, il est toujours possible de trouver une extension du champ qui a le groupe donné que son groupe de Galois. Elle réduit cela à " le problème de Noether ", qui demande si le champ fixe d'un sous-groupe G de la groupe de permutation S n agissant sur le champ k ( x 1 , ..., x n ) est toujours un pur l'extension du champ transcendantal k . (Elle a d'abord mentionné ce problème dans un document 1913, où elle a attribué le problème à son collègue Fischer.) Elle a montré cela était vrai pour n = 2 , 3, ou 4. En 1969, RG Swan trouvé un contre-exemple au problème de Noether , avec n = 47 et G un groupe cyclique de l'ordre de 47 (bien que ce groupe peut être réalisé comme un groupe de Galois sur les rationnels à d'autres moyens). Le problème inverse de Galois reste entier.
Physique
Noether a été porté à Göttingen en 1915 par David Hilbert et Felix Klein, qui voulait son expertise dans la théorie des invariants pour les aider dans la compréhension de la relativité générale , une théorie géométrique de la gravitation développé principalement par Albert Einstein . Hilbert avait observé que la conservation de l'énergie semblait être violés dans la relativité générale, en raison du fait que l'énergie gravitationnelle pourrait se déplacera. Noether fourni la résolution de ce paradoxe, et un outil fondamental de moderne physique théorique, avec premier théorème de Noether, qui elle a prouvé en 1915, mais n'a pas publié jusqu'en 1918. Elle a résolu le problème non seulement pour la relativité générale, mais a déterminé les quantités conservées pour chaque système de lois physiques qui possède une certaine symétrie continue.
Dès réception de son travail, Einstein écrivait à Hilbert:. «Hier, je reçus de Mlle Noether un document très intéressant sur les invariants Je suis impressionné que de telles choses peuvent être compris de manière générale La vieille garde à Göttingen devrait prendre quelques leçons de. Mlle Noether! Elle semble connaître son truc. "
À titre d'illustration, si un système physique se comporte de la même, peu importe comment il est orienté dans l'espace, les lois physiques qui régissent sont symétrie de rotation; à partir de cette symétrie, le théorème de Noether montre le moment angulaire du système doit être conservée. Le système physique lui-même ne doivent pas nécessairement être symétrique; un astéroïde déchiquetée tumbling dans l'espace conserve moment angulaire en dépit de son asymétrie. Plutôt, la symétrie des lois physiques régissant le système est responsable de la loi de conservation. Comme autre exemple, si une expérience de physique a le même résultat en tout lieu et à tout moment, alors ses lois sont symétriques sous traductions continues dans l'espace et le temps; par le théorème de Noether, ces symétries représentent les lois de conservation de quantité de mouvement et de l'énergie au sein de ce système, respectivement.
Le théorème de Noether est devenu un outil fondamental de moderne physique théorique, à la fois en raison de la perspicacité qu'il donne dans les lois de conservation, et aussi, comme un outil de calcul pratique. Son théorème permet aux chercheurs pour déterminer les quantités conservées à partir des symétries observées d'un système physique. A l'inverse, il facilite la description d'un système physique sur la base de classes de lois physiques hypothétiques. À titre d'illustration, supposons qu'un phénomène physique nouveau est découvert. Le théorème de Noether fournit un test pour les modèles théoriques du phénomène: si la théorie a une symétrie continue, alors le théorème de Noether garantit que la théorie a une quantité conservée, et pour la théorie soit correcte, cette conservation doit être visible dans les expériences.
Deuxième époque (1920-1926)
Bien que les résultats de la première époque de Noether étaient impressionnants et utiles, sa renommée en tant que mathématicien repose davantage sur le travail de pionnier qu'elle a fait dans ses deuxième et troisième époques, comme l'a noté Hermann Weyl et BL van der Waerden dans leurs nécrologies de son.
Dans ces époques, elle n'a pas été fait qu'appliquer des idées et des méthodes de mathématiciens antérieures; plutôt, elle a été l'élaboration de nouveaux systèmes de définitions mathématiques qui seraient utilisés par les futurs mathématiciens. En particulier, elle a développé une théorie complètement nouvelle des idéaux en anneaux, en généralisant les travaux antérieurs de Richard Dedekind. Elle est également réputée pour le développement croissant des conditions de la chaîne, une condition de finitude simple qui a donné des résultats puissants dans ses mains. Ces conditions et la théorie des idéaux permis Noether de généraliser les résultats de nombreux anciens et de traiter de vieux problèmes sous un nouvel angle, comme la théorie de l'élimination et les variétés algébriques qui avaient été étudiés par son père.
Monter et descendre les conditions de la chaîne
A cette époque, Noether est devenu célèbre pour son usage habile de croissant (Teilerkettensatz) ou décroissant (Vielfachenkettensatz) conditions de la chaîne. Une séquence de non videssous-ensembles A 1,A 2,A 3, etc. d'unensemble Sest généralement dit êtreascendant, si chacun est un sous-ensemble de la prochaine
Inversement, une séquence de sous-ensembles deSest appelédécroissantsi chacun contient la prochaine sous-ensemble:
Une chaîne devient constante après un nombre fini d'étapes si il existe un n tel que 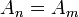 pour tout m ≥ n . Une collection de sous-ensembles d'un ensemble donné satisfait à la condition de chaîne ascendante si aucune séquence ascendante devient constante après un nombre fini d'étapes. Il satisfait à la condition de la chaîne de descente si aucune séquence descendante devient constante après un nombre fini d'étapes.
pour tout m ≥ n . Une collection de sous-ensembles d'un ensemble donné satisfait à la condition de chaîne ascendante si aucune séquence ascendante devient constante après un nombre fini d'étapes. Il satisfait à la condition de la chaîne de descente si aucune séquence descendante devient constante après un nombre fini d'étapes.
Croissant et de la chaîne descendante conditions sont en général, ce qui signifie qu'ils peuvent être appliqués à de nombreux types d'objets mathématiques et, sur la surface, ils pourraient semblent pas très puissant. Noether a montré comment exploiter ces conditions, cependant, pour profiter au maximum: par exemple, comment les utiliser pour montrer que chaque ensemble de sous-objets a une / élément minimal de maximale ou un objet complexe peut être généré par un plus petit nombre d'éléments . Ces conclusions sont souvent des étapes cruciales dans une preuve.
De nombreux types d'objets dans l'algèbre abstraite peuvent satisfaire aux conditions de la chaîne, et habituellement si elles satisfont à une condition de la chaîne de croissant, ils sont appelés Noethérien en son honneur. par définition, un anneau noethérien satisfait une condition de chaîne ascendant sur ses idéaux à gauche et à droite, tandis qu'un groupe nœthérien est défini comme un groupe dans lequel chaque chaîne strictement croissant de sous-groupes est finie. Un nœthérien Module est un module dans lequel chaque chaîne strictement croissant de sous-modules se brise après un nombre fini. Un nœthérien espace est un espace topologique dans lequel chaque chaîne strictement croissante de sous-espaces ouverts rompt après un nombre fini de termes; cette définition est faite de sorte que le spectre d'un anneau noethérien est un espace topologique noethérien.
La condition de la chaîne est souvent "hérité" de sous-objets. Par exemple, tous les sous-espaces d'un espace noethérien, sont eux-mêmes noethérien; tous les sous-groupes et groupes quotients d'un groupe nœthérien sont également, noethérien; et, mutatis mutandis , la même chose pour les sous-modules et modules de quotient d'un module noethérien. Tous les anneaux quotients d'un anneau noethérien sont noethérien, mais qui ne tient pas nécessairement pour ses sous-anneaux. La condition de la chaîne peut également être hérité par des combinaisons ou des extensions d'un objet noethérien. Par exemple, sommes directes finies de bagues noethériens sont noethérien, tout comme la bague de mise en série de puissance sur un anneau noethérien.
Une autre application de ces conditions de la chaîne est en nœthérien induction aussi connu comme induction qui le bien-fondé est une généralisation de l'induction mathématique. Il est fréquemment utilisé pour réduire des déclarations générales sur les collections d'objets à des déclarations sur des objets spécifiques de cette collection. Supposons que S est un ensemble partiellement ordonné. Une manière de prouver une déclaration sur les objets de S est de supposer l'existence d'un contre-exemple et en déduire une contradiction, prouvant ainsi la contraposée de la déclaration originale. Le principe de base de l'induction nœthérien est que chaque sous-ensemble non vide de S contient un élément minimal. En particulier, l'ensemble des contre-exemples contient un élément minimal, la contre-minime . Afin de prouver la déclaration originale, donc, il suffit de prouver quelque chose d'apparemment beaucoup plus faible: Pour toute contre-exemple, il ya un contre-petits.
Commutatives anneaux, idéaux, et de modules
Le document de Noether, Idealtheorie dans Ringbereichen ( Théorie des Idéaux Anneau Domaines , 1921), est le fondement de la théorie générale de anneau commutatif, et donne une des premières définitions générales d'un anneau commutatif . Avant son document, la plupart des résultats en algèbre commutative ont été limitées à des exemples particuliers des anneaux commutatifs, tels que des anneaux de polynômes sur les champs ou l'anneau des entiers algébriques. Noether prouvé que dans un anneau qui satisfait la condition de la chaîne ascendant sur idéaux, tout idéal est de type fini. En 1943, le mathématicien français Claude Chevalley a inventé le terme, anneau noethérien , pour décrire cette propriété. Un résultat majeur en 1921 papier de Noether est le théorème Lasker-Noether , qui étend le théorème de Lasker sur la décomposition primaire des idéaux de anneaux de polynômes à tous les anneaux noethériens. Le théorème Lasker-Noether peut être considérée comme une généralisation du théorème fondamental de l'arithmétique qui stipule que tout nombre entier positif peut être exprimée comme un produit de nombres premiers , et que cette décomposition est unique.
Travaux de Noether Abstrakter Aufbau der Idealtheorie dans algebraischen Zahl- und Funktionenkörpern ( Résumé Structure de la théorie de Idéaux algébrique nombre et la fonction Fields , 1927) caractérise les anneaux dans lequel les idéaux ont factorisation unique des idéaux premiers que les domaines de Dedekind: domaines intégrales qui sont noethérien, 0 ou 1 dimensions, et intégralement clos dans leurs domaines de quotient. Ce document contient aussi ce que l'on appelle maintenant les théorèmes d'isomorphisme, qui décrivent certains fondamentaux isomorphismes naturels, et quelques autres résultats de base sur noethériens et modules Artinian.
la théorie de l'élimination
En 1923-24, Noether appliqué sa théorie idéale pour l'élimination théorie dans une formulation qu'elle attribue à son élève, Kurt-Hentzelt montrant que les théorèmes fondamentaux sur la factorisation de polynômes pourraient être reportées directement. Traditionnellement, théorie d'élimination est préoccupé par l'élimination d'un ou plusieurs variables à partir d'un système d'équations polynomiales, généralement par le procédé de résultantes. Pour illustration, le système d'équations peut souvent être écrit sous la forme d'une matrice M (manque la variable x ) fois un vecteur v (ayant seulement différentes puissances de x ) égalant le vecteur nul, M • v = 0 . Par conséquent, le déterminant de la matrice M doit être égal à zéro, la fourniture d'une nouvelle équation où la variable x a été éliminé.
La théorie des invariants des groupes finis
Des techniques telles que la solution non-constructive originale de Hilbert au problème de base finie ne pouvaient pas être utilisés pour obtenir des informations quantitatives sur les invariants d'une action de groupe, et en outre, ils ne sont pas applicables à toutes les actions de groupe. Dans son document de 1915, Noether a trouvé une solution au problème de base finie pour un groupe fini de transformations G agissant sur un espace vectoriel de dimension finie sur un champ de caractéristique nulle. Sa solution montre que l'anneau des invariants est généré par invariants homogènes dont le degré est inférieur ou égal à l'ordre du groupe fini; on appelle cela, Noether est lié . Son papier a donné deux preuves de Noether est lié, qui tous deux travaillent également lorsque la caractéristique du champ est premier avec | G | !, la factorielle de l'ordre | G | du groupe G . Le nombre de générateurs ne doit pas nécessairement satisfaire de Noether liée lorsque la caractéristique du champ divise le | G |, mais Noether n'a pas pu déterminer si la tenue est correcte lorsque la caractéristique du champ divise | G |! mais pas | G |. Pendant de nombreuses années, la détermination de la vérité ou la fausseté de la limite dans ce cas était un problème ouvert disant «écart de Noether". Il a finalement été résolu de façon indépendante par Fleischmann en 2000 et Fogarty en 2001, qui ont tous deux montré que la limite reste vrai.
Dans son document de 1926, Noether étendu le théorème de Hilbert à des représentations d'un groupe fini sur tous les domaines; le nouveau cas qui ne suivait pas du travail de Hilbert, est lorsque la caractéristique du champ divise l'ordre du groupe. Le résultat de Noether a ensuite été étendu par William Haboush à tous les groupes réductrices par sa démonstration de la conjecture de Mumford. Dans cet article Noether a également présenté le Noether normalisation lemme , montrant qu'un type fini domaine A sur un champ k dispose d'un ensemble x 1 , ..., x n des éléments algébriquement indépendants tels que A est intégrale sur k [ x 1 , ..., x n ] .
Contributions à la topologie

Comme l'a noté Pavel Alexandrov et Hermann Weyl dans leurs nécrologies, les contributions de Noether à topologie illustrent sa générosité avec les idées et la façon dont ses idées pourraient transformer des champs entiers de mathématiques. En topologie, les mathématiciens étudient les propriétés des objets qui restent invariant même sous déformation, propriétés telles que leur connectivité. Une plaisanterie courante est qu'une topologist ne peut pas distinguer un beignet d'une tasse de café, car ils peuvent être déformés en permanence dans un autre.
Noether est crédité avec les idées fondamentales qui ont conduit à l'élaboration de la topologie algébrique de la première topologie combinatoire, en particulier, l'idée de groupes d'homologie. Selon le récit de Alexandrov, Noether assisté à des conférences données par Heinz Hopf et lui au cours des étés 1926 et 1927, où "elle a continuellement fait des observations, qui étaient souvent profonde et subtile" et il poursuit en disant que,
Lorsque ... elle est d'abord connaissance avec une construction systématique de topologie combinatoire, elle a immédiatement observé qu'il serait intéressant d'étudier directement les groupes de complexes algébriques et des cycles d'un polyèdre donné et le sous-groupe du groupe de cycle étant constitué de cycles homologues zéro; au lieu de la définition usuelle de nombres de Betti, elle suggère immédiatement définissant le groupe Betti comme le groupe complémentaire (quotient) du groupe de tous les cycles du sous-groupe de cycles homologue à zéro. Cette observation semble maintenant évidente. Mais dans ces années (1925- 28 ), ce fut un tout nouveau point de vue.
La suggestion de Noether que topologie algébrique être étudiée, a été adopté immédiatement par Hopf, Alexandrov, et d'autres, et il est devenu un sujet de discussion fréquent parmi les mathématiciens de Göttingen. Noether observé que son idée d'un groupe Betti rend la formule d'Euler-Poincaré simple à comprendre, et de son propre travail de Hopf sur ce sujet "porte l'empreinte de ces remarques de Emmy Noether". Noether mentionne ses propres idées de topologie en aparté seulement dans une publication 1926, où elle cite comme une application de la théorie des groupes .
L'approche algébrique à la topologie a été développé indépendamment en Autriche . Dans un cours donné en 1926-1927 Vienne , Leopold Vietoris a défini un groupe d'homologie, qui a été développé par Walther Mayer, dans une définition axiomatique en 1928.

Troisième époque (1927-1935)
Numéros hypercomplexes et théorie de la représentation
Beaucoup de travail sur les numéros de hypercomplexes et représentations de groupes a été réalisée au XIXe et début du XXe siècles, mais reste disparate. Noether uni les résultats et a donné la première théorie de la représentation générale des groupes et algèbres. Brièvement, Noether subsumé la théorie de la structure des algèbres associatives et la théorie de la représentation des groupes dans une théorie arithmétique simple des modules et des idéaux à anneaux satisfaisant les conditions de la chaîne ascendante. Ce travail unique par Noether était d'une importance fondamentale pour le développement de l'algèbre moderne.
Algèbre non commutative
Noether a également été responsable d'un certain nombre d'autres avancées dans le domaine de l'algèbre. Avec Emil Artin,Richard Brauer, etHelmut Hasse, elle a fondé la théorie desalgèbres centrales simples.
Un article fondamental par Noether, Helmut Hasse, et Richard Brauer concerne algèbres de division, qui sont des systèmes algébriques dans laquelle la division est possible. Ils ont prouvé deux théorèmes importants: un théorème local-global indiquant que si une dimension algèbre de division centrale fini sur un champ de numéro divise localement partout alors il divise le monde (il en est trivial), et à partir de cela, déduite de leur Hauptsatz ("théorème principal") : chaque dimension finie centrale algèbre de division sur un nombre algébrique champ F divise sur une prolongation cyclotomique cyclique . Ces théorèmes permettent de classer toutes les dimensions algèbres de division centrale fini sur un champ de numéro donné. Un document ultérieur par Noether a montré, comme un cas particulier d'un théorème plus général, que tous les sous-champs maximaux d'une division algèbre D sont champs fractionnement. Ce document contient également le théorème de Skolem-Noether qui stipule que les deux plongements d'une extension d'un champ k dans une dimension algèbre centrale simple fini sur k , sont conjugués. Le Brauer-Noether théorème donne une caractérisation des champs d'une division centrale de séparation algèbre sur un champ.
Évaluation, de reconnaissance, et mémoriaux

Le travail de Noether continue d'être pertinent pour le développement de la physique théorique et les mathématiques et elle est régulièrement classé comme l'un des plus grands mathématiciens du XXe siècle. Dans sa nécrologie, compatriote algebraist BL van der Waerden dit que son originalité mathématique était "absolu au-delà de la comparaison", et Hermann Weyl dit que Noether "changé le visage de l'algèbre par son travail ". Au cours de sa vie et même jusqu'à aujourd'hui, Noether a été caractérisé comme le plus grand mathématicien de femme dans l'histoire enregistrée par les mathématiciens tels que Pavel Alexandrov, Hermann Weyl, et Jean Dieudonné.
Dans une lettre à Le New York Times,Albert Einsteina écrit:
Dans l'arrêt des mathématiciens vivants les plus compétents, Fräulein Noether était la mathématique créative la plus importante génie jusqu'ici produites depuis l'enseignement supérieur des femmes a commencé. Dans le domaine de l'algèbre, dans lequel les mathématiciens les plus doués ont été occupés pendant des siècles, elle a découvert des méthodes qui se sont avérées d'une importance énorme dans le développement de l'actuelle génération de jeunes mathématiciens.
Le 2 Janvier 1935, quelques mois avant sa mort, mathématicienNorbert Wiener a écrit que
Mlle Noether est ... le plus grand mathématicien de femme qui ait jamais vécu; et la plus grande femme scientifique de toute sorte qui vit maintenant, et un érudit au moins sur le plan de Madame Curie .
Lors d'une exposition à la 1964Salon mondial consacré auxmathématiciens modernes, Noether était la seule femme représentée parmi les mathématiciens remarquables du monde moderne.
Noether a été honoré dans plusieurs mémoriaux,
- Le Association pour les femmes en mathématiques est titulaire d'un noether lecture pour honorer les femmes en mathématiques chaque année; dans sa brochure 2005 pour l'événement, l'Association caractérise Noether comme «l'un des grands mathématiciens de son temps, quelqu'un qui a travaillé et lutté pour ce qu'elle aimait et croyait. Sa vie et de travail restent une formidable source d'inspiration".
- Conformément à son dévouement envers ses étudiants, l'Université de Siegen abrite ses mathématiques et les départements de physique dans les bâtiments surle campus Emmy Noether.
- La Fondation allemande de recherche (Deutsche Forschungsgemeinschaft) exploite leprogramme Emmy Noether, une bourse d'études fournissant des fonds aux jeunes chercheurs prometteurs post-doctorants dans leurs nouvelles activités de recherche et d'enseignement.
- Une rue dans sa ville natale, Erlangen, a été nommé d'après Emmy Noether et son père, Max Noether.
- Le successeur de l'école secondaire, elle a assisté à Erlangen a été renommél'école Emmy Noether.
Dans la fiction, Emmy Nutter, le professeur de physique dans «Le Dieu des brevets" par Ransom Stephens, est basée sur Emmy Noether
Loin de la maison,
- Le cratère Nöther sur laface cachée de la lune est nommé d'après elle.
- Le 7001 Noether astéroïde est également nommé pour Emmy Noether.
Liste des doctorants
| Date | Nom de l'étudiant | Titre de la thèse et traduction anglaise | Université | Publication | |
|---|---|---|---|---|---|
| 16/12/1911 | Falckenberg, Hans | Verzweigungen von Lösungen nichtlinearer Differentialgleichungen
| Erlangen | Leipzig 1912 | |
| 04/03/1916 | Seidelmann, Fritz | Die Gesamtheit der kubischen und biquadratischen Gleichungen mit Affekt bei beliebigem Rationalitätsbereich
| Erlangen | Erlangen 1916 | |
| 25/02/1925 | Hermann, Grete | Die Frage der endlich vielen Schritte in der Theorie der Polynomideale unter Benutzung nachgelassener Sätze von Kurt Hentzelt
| Göttingen | Berlin 1926 | |
| 14/07/1926 | Grell, Heinrich | Beziehungen zwischen den Idealen verschiedener Ringe
| Göttingen | Berlin 1927 | |
| 1927 | Dorate, Wilhelm | Berlin 1934 | |||
| 06/12/1933 | Tsen, Chiungtze | Algebren über Funktionenkörpern
| Göttingen | Göttingen 1934 | |
| 1934 | Schilling, Otto | Qui gewisse Beziehungen der zwischen Arithmetik hyperkomplexer Zahlsysteme und algebraischer Zahlkörper
| Marburg | Braunschweig 1935 | |
| 1935 | Stauffer, Ruth | La construction d'une base normale dans une zone d'extension séparable | Bryn Mawr | Baltimore 1936 | |
| 1935 | Vorbeck, Werner | Nichtgaloissche Zerfällungskörper einfacher Systeme
| Göttingen | ||
| 1936 | Wichmann, Wolfgang | Anwendungen der p-adischen Theorie im Nichtkommutativen
| Göttingen | Monatshefte für Mathematik und Physik(1936)44, 203-24. |
Sujets mathématiques éponymes
|
|
|