Elementos de Euclides

O frontispício da primeira versão Inglês de Sir Henry Billingsley dos Elementos de Euclides, 1570

Elementos de Euclides ( grego : Στοιχεῖα) é um matemático e geométrico tratado constituído por 13 livros escritos pelo Grego matemático Euclides em Alexandria por volta de 300 aC. É composto por uma coleção de definições, postulados ( axiomas), proposições ( teoremas e construções ), e provas matemáticas das proposições. Os treze livros cobrem a geometria euclidiana ea versão antiga grega de elementar teoria dos números . Com a exceção de Autolycus 'On the Sphere em Movimento, o Elements é um dos mais antigos tratados matemáticos gregos existentes e é a mais antiga tratamento dedutivo axiomático existente da matemática . Ele provou instrumental no desenvolvimento da lógica e moderna ciência .

Elementos de Euclides é o livro mais bem sucedida e influente alguma vez escrito. Sendo definida pela primeira vez no tipo de Veneza em 1482, que é um dos primeiros trabalhos muito matemáticos para ser impresso depois da invenção da imprensa e só perde para a Bíblia no número de edições publicadas, com o número chegando a mais de mil. Foi usado como texto de base da geometria em todo o mundo ocidental por cerca de 2.000 anos. Durante séculos, quando o quadrivium foi incluído no currículo de todos os estudantes universitários, o conhecimento de pelo menos parte dos Elementos de Euclides era exigido de todos os alunos. Não até o século 20, época em que o seu conteúdo foi universalmente ensinado através de livros escolares, é que ele deixa de ser considerado algo que todas as pessoas educadas tinha lido.

História

O frontispício de um Adelard de tradução Bath Latina de Elementos de Euclides, c. 1309-1316; a tradução mais velho sobrevivente Latina do Elements é uma obra do século 12 por Adelard, que se traduz em latim do árabe.

Euclides era um Matemático grego que escreveu Elements em Alexandria durante o Período helenístico (cerca de 300 aC). Estudiosos acreditam que o Elements é em grande medida uma coleção de teoremas provados por outros matemáticos, bem como contendo algum trabalho original. Proclus, um matemático grego que viveu vários séculos depois de Euclides, escreve em seu comentário dos Elementos: "Euclides, que reuniu o Elements, recolhendo muitos dos Teoremas Eudoxus ', aperfeiçoando muitos dos Teeteto, e também trazendo à demonstração irrefutável as coisas que foram apenas um pouco vagamente provadas por seus antecessores ".

Embora conhecida a, por exemplo, Cícero, não há registro existente do texto ter sido traduzido para o latim antes Boécio, no quinto ou sexto século. Os árabes receberam os elementos dos bizantinos em aproximadamente 760; Nesta versão, por um aluno de Euclides chamado Proclo, foi traduzido para o árabe sob Harun al Rashid circa 800 AD. A primeira edição impressa apareceu em 1482 (com base na Giovanni Campano de Edição 1260), e desde então tem sido traduzido em muitas línguas e publicada em cerca de mil edições diferentes. Em 1570, John Dee forneceu um muito respeitado "prefácio matemático", junto com anotações e material suplementar, para a primeira edição Inglês por Henry Billingsley.

Cópias do texto grego ainda existem, alguns dos quais podem ser encontrados na Biblioteca e do Vaticano Biblioteca Bodleian, em Oxford. Os manuscritos disponíveis são de qualidade variável, e invariavelmente incompleto. Pela análise cuidadosa das traduções e originais, hipóteses foram tiradas sobre o conteúdo do texto original (cópias de que já não estão disponíveis).

Textos antigos que se referem ao próprio Elements e outras teorias matemáticas que eram correntes na época em que foi escrita também são importantes neste processo. Tais análises são conduzidas pela JL Heiberg e Sir Thomas Pouco Heath em suas edições de texto.

Também de importância são o scholia, ou anotações ao texto. Estes aditamentos, que muitas vezes distinguem-se do texto principal (dependendo do manuscrito), acumulado gradualmente ao longo do tempo como opiniões variadas sobre o que era digno de explicação ou esclarecimento. Alguns destes são úteis e adicionar ao texto, mas não são muitos.

Um texto difícil

Embora agora consideramos os elementos para ser um texto elementar sobre geometria, que não foi sempre o caso. Diz-se que o Rei Ptolomeu pediu uma maneira em geometria que foi menor do que os Elements. Euclid respondeu que "não há nenhuma estrada real para a geometria. "Mais recentemente, Sir Thomas Pouco Heath escreveu, na introdução à Biblioteca de 1932 do Everyman Euclid Introdução

"A verdade simples é que ele não foi escrito para estudantes ou estudantes, mas para o homem adulto que teria o conhecimento e julgamento necessárias para apreciar as questões contenciosas que têm muito que ser ultrapassadas em qualquer tentativa de estabelecer os fundamentos de Euclidiana geometria como estritamente sistema lógico ... ".

A primeira passagem difícil do Livro I é referido como o pons Asinorum, que é Latin para "Ponte de Asses" (tradicionalmente, é difícil de obter burros que atravessar uma ponte).

Esboço dos Elementos

Uma prova de Elementos de Euclides que, dado um segmento de linha, existe um triângulo equilátero que inclui o segmento como um de seus lados. A prova é de construção: um triângulo equilátero ΑΒΓ é feita por desenho círculos Δ Ε e centrados nos pontos Α e Β, e tendo uma intersecção dos círculos como o terceiro vértice do triângulo.

O Elements ainda é considerado uma obra-prima na aplicação de lógica para a matemática . No contexto histórico, tem-se revelado extremamente influente em muitas áreas da ciência . Cientistas Nicolau Copérnico , Johannes Kepler , Galileu Galilei , e Sir Isaac Newton foram todos influenciados pelos elementos, e aplicaram seu conhecimento dela ao seu trabalho. Os matemáticos e filósofos, como Bertrand Russell , Alfred North Whitehead, e Baruch Spinoza , tentaram criar seus próprios "Elementos" fundamentais para suas respectivas disciplinas, ao adoptar as estruturas dedutivas axiomatizada que a obra de Euclides introduzidas.

O sucesso dos Elementos é devido principalmente à sua apresentação lógica da maior parte do conhecimento matemático disponível para Euclid. Grande parte do material não é original com ele, embora muitas das provas são dele. No entanto, o desenvolvimento sistemático de Euclides de seu tema, a partir de um pequeno conjunto de axiomas para resultados profundos, ea consistência de sua abordagem em todo o Elements, encorajou o seu uso como um livro para cerca de 2.000 anos. O Elements ainda influencia livros de geometria modernos. Além disso, sua abordagem axiomática lógica e provas rigorosas permanecer a pedra angular da matemática.

Embora Elements é essencialmente um trabalho geométrico, que também inclui os resultados que hoje seria classificado como teoria dos números . Euclid provavelmente escolheu para descrever resultados em teoria dos números em termos de geometria, porque ele não poderia desenvolver uma abordagem constructible a aritmética. A construção usado em qualquer das provas de Euclides necessária uma prova de que é realmente possível. Isso evita os problemas encontrados com os pitagóricos irracionais, já que suas provas falaciosos geralmente necessária uma declaração como "Localizar a maior medida comum de ..."

Primeiros princípios

De Euclides Livro 1 começa com 23 definições - como ponto, linha , e superfície - seguido por cinco postulados e cinco "noções comuns" (sendo que ambos são hoje chamados axiomas). Estes são a base de tudo o que se segue.

Postula:

1. Um segmento de reta pode ser que une dois pontos quaisquer.
2. Um segmento de reta pode ser prorrogado indefinidamente em uma linha reta.
3. Dado um segmento de reta, um círculo pode ser desenhado com o segmento como um raio e ponto final como centro.
4. Todos os ângulos retos são iguais.
5. Se duas linhas são desenhadas que se cruzam de um terço de tal maneira que a soma dos ângulos internos de um dos lados é inferior a dois ângulos rectos, em seguida, as duas linhas se cruzam, inevitavelmente, deve-se mutuamente sobre que lado se estendia muito suficiente.

Noções comuns:

1. O que equivale a mesma coisa que são iguais um ao outro. ( Propriedade euclidiana de igualdade)
2. Se iguais forem adicionados a iguais, então as somas são iguais. (Propriedade adição de igualdade)
3. Se iguais são subtraídos iguais, então os restantes são iguais. (Propriedade da subtração da igualdade)
4. O que coincidem um com o outro são iguais um ao outro. ( Propriedade reflexiva da igualdade)
5. O todo é maior do que a parte.

Estes princípios básicos refletir o interesse de Euclides, junto com seus matemáticos gregos e helenistas contemporâneas, na geometria construtiva. Os três primeiros postulados basicamente descrever as construções pode-se realizar com um bússola e um não marcado régua. A marcada régua, utilizado em construção neusis, é proibido na construção Euclid, provavelmente porque Euclides não podia provar que as linhas beirando atender.

Postulado paralelo

Se a soma dos dois ângulos internos é igual a 180 °, as linhas são paralelas e nunca se intersectam.

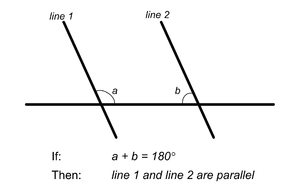
O último dos cinco postulados de Euclides merece menção especial. A chamada postulado paralelo sempre parecia menos óbvia do que os outros. O próprio Euclides usou apenas moderadamente ao longo do resto dos elementos. Muitos geometers suspeita de que poderia ser dedutível dos outros postulados, mas todas as tentativas de fazer isso falhou.

Em meados do século 19 , foi demonstrado que tal prova existe, porque pode-se construir geometrias não-euclidianas, onde o postulado das paralelas é falso, enquanto os outros postulados permanecer fiel. Por esta razão, matemáticos dizer que o postulado é paralelo independente dos outros postulados.

Duas alternativas para o postulado das paralelas são possíveis em geometrias não-euclidianas: ou um número infinito de linhas paralelas podem ser tiradas através de um ponto e não em uma linha reta em um geometria hiperbólica (também chamado Geometria Lobachevskian), ou nenhum pode, em um geometria elíptica (também chamada Geometria Riemanniana). Que outras geometrias poderia ser logicamente consistente foi uma das mais importantes descobertas em matemática, com vastas implicações para a ciência ea filosofia. Na verdade, Albert Einstein teoria da 's relatividade geral mostra que o espaço real em que vivemos é não-euclidiana.

Conteúdo dos livros

Um fragmento de elementos de Euclides encontrada em Oxyrhynchus , que é datada de cerca de 100 AD. O diagrama acompanha Proposição 5 do Livro II do Elements.

Livros de 1 a 4 acordo com geometria plana:

• Livro 1 contém as proposições básicas de geometria: o teorema de Pitágoras (Proposição 47), a igualdade de ângulos e áreas , paralelismo, a soma dos ângulos de um triângulo e os três casos em que triângulos são "iguais" (ter a mesma área ).
• Livro 2 é comumente chamado de "livro de álgebra geométrica," porque o material que ele contém podem facilmente ser interpretada em termos de álgebra .
• Livro 3 lida com círculos e suas propriedades: ângulos inscritos, tangentes , o poder de um ponto.
• Livro 4 está preocupado com inscrevendo e circunscrevendo e triângulos polígonos regulares.

Livros de 5 a 10 introduzir e rácios proporções:

• Livro 5 é um tratado sobre proporções de magnitudes.
• Livro 6 aplica-se proporções de geometria: O teorema de Thales, figuras semelhantes.
• Livro 7 trata estritamente com a teoria elementar número: divisibilidade , números primos , máximo divisor comum , mínimo múltiplo comum.
• Livro 8 trata de proporções na teoria dos números e sequências geométricas.
• Livro 9 aplica-se os resultados dos anteriores dois livros: a infinitude dos números primos, a soma de uma série geométrica, números perfeitos .
• Reserve 10 tentativas de classificar incomensuráveis (em linguagem moderna, irracional ) magnitudes, utilizando o método de exaustão, um precursor para a integração .

Livros 11 a 13 lidar com geometria espacial:

• Livro 11 generaliza os resultados de Livros 1-6 ao espaço: perpendicularidade, paralelismo, volumes de paralelepípedos.
• Reservar 12 calcula áreas e volumes usando o método de exaustão: cones, pirâmides, cilindros, ea esfera .
• Reservar 13 generaliza Livro 4 ao espaço: seção áurea , os cinco regulares sólidos platônicos inscritas em uma esfera.

Crítica

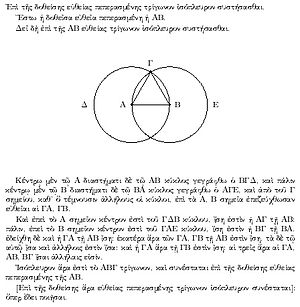
Apesar de sua aceitação e sucesso universal, o Elements tem sido criticado como tendo provas e definições insuficientes. Por exemplo, na primeira construção de um livro, Euclides utilizada uma premissa de que nem foi postulada nem revelou: que dois círculos com centros à distância do seu raio vai intersectar em dois pontos. Mais tarde, na quarta construção, ele utilizado o movimento de triângulos para provar que se dois lados e os seus ângulos são iguais, então eles são congruentes; no entanto, ele não postular ou mesmo definir o movimento.

No século 19, as geometrias não-euclidianas atraiu a atenção dos matemáticos contemporâneos. Matemáticos de renome, incluindo Richard Dedekind e David Hilbert , tentou reformular os axiomas dos elementos, como pela adição de um axioma de continuidade e um axioma da congruência, para fazer geometria euclidiana mais completa.

O matemático e historiador WW Rouse Bola de colocar as críticas em perspectiva, observando que "o fato de que há dois mil anos [os elementos] foi o livro-texto de costume sobre o assunto levanta uma forte suspeita de que ele não é adequado para o efeito."

Apocrypha

Não era incomum no tempo antigo atribuir a autores célebres obras que não foram escritos por eles. É por esses meios que os apócrifos livros XIV e XV dos Elementos às vezes eram incluídos na coleção. O espúria Livro XIV foi provavelmente escrito por Hypsicles sobre a base de um tratado por Apolônio. O livro de Euclides comparador continua de sólidos regular inscrito em esferas, com o principal resultado é que a relação entre as superfícies do dodecaedro e icosaedro inscrito na mesma esfera é a mesma que a relação de seus volumes, sendo a razão .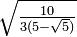

O espúria Livro XV foi provavelmente escrito, pelo menos em parte, por Isidoro de Mileto. Este livro inferior abrange temas como a contagem do número de arestas e ângulos sólidos nos sólidos regulares, e encontrar a medida de ângulos diedros de rostos que se encontram em uma borda.

Edições

O italiano Jesuíta Matteo Ricci (esquerda) e do Matemático chinês Xu Guangqi (à direita) publicou o chinês edição dos Elementos de Euclides (幾何原本) em 1607.

• 1460s, Regiomontanus (incompleto)
• 1533 editio princeps por Simon Grynäus
• 1572, Commandinus
• 1574, Christoph Clavius

Traduções

• 1505, Zamberti (Latin)
• 1543, Venturino Ruffinelli (Italiano)
• 1555, Johann Scheubel (Alemão)
• 1562, Jacob Kündig (Alemão)
• 1564, Pierre Forcadel de Beziers (francês)
• 1570, John Day (Inglês)
• 1576, Rodrigo de Zamorano (Espanhol)
• 1594, Typografia Medicea (edição da tradução árabe Nasir al-Din al-Tusi)
• 1607, Matteo Ricci, Xu Guangqi (Chinese)
• 1660, Isaac Barrow (Inglês)
• Presente, Irineu Bicudo (Português) (work in progress)

Actualmente no impressão

"Elementos de Euclides - Todos os treze livros em um volume" Green Lion Press. ISBN 1-888009-18-7 Com base em tradução de Heath.