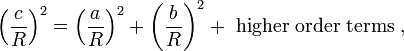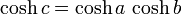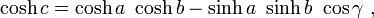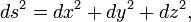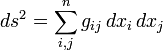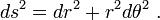Teorema de Pitágoras
Fundo para as escolas Wikipédia
Crianças SOS tentou tornar o conteúdo mais acessível Wikipedia por esta selecção escolas. Visite o site da SOS Children at http://www.soschildren.org/
| Trigonometria |
|---|
| História Uso Funções Generalized Funções inversas Outras leituras |
| Referência |
| Identidades Constantes exatas Tabelas trigonométricas |
| Leis e teoremas |
| Lei de senos Lei dos cossenos Lei das tangentes Lei de cotangentes Teorema de Pitágoras |
| Cálculo |
| Substituição trigonométrica Integrais de funções Derivados de funções Integrais de funções inversas |
| Geometria |
|---|
 Oxyrhynchus papiro (P.Oxy. I 29), mostrando fragmento de Elementos de Euclides |
| História da geometria |
Ramos Geometria euclidiana · Euclidiana não geometria · A geometria analítica · Geometria Riemanniana · A geometria diferencial · Geometria projetiva · Geometria Algébrica |
Áreas de pesquisa |
Conceitos importantes · Ponto Linha · Perpendicular · Paralela · Segmento de linha · Ray · Plano · Comprimento · Área · Volume · Vertex · Ângulo · Congruência · Similaridade · Polygon · Triângulo · Altitude · · Hipotenusa teorema de Pitágoras · Quadrilátero · Trapézio · Pipa Paralelogramo ( Rhomboid, Retângulo, Rhombus, Praça ) · Diagonal · Simetria · Curva · Círculo · Área de um disco · Circunferência · Diâmetro · Cilindro · Esfera · Pirâmide · Dimensões ( um, dois, três, quatro) |
Geômetras Aryabhata · Ahmes · Apolônio · Archimedes · Baudhayana · Bolyai · Brahmagupta · Euclid · Pitágoras · Khayyám · Descartes · Pascal · Euler · Gauss · Ibn al-Yasamin · Jyesthadeva · Katyayana · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · Poincaré · Sijzi · Hilbert · Minkowski · Cartan · Veblen · Sakabe Kohan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng |
Em matemática , o teorema de Pitágoras - ou teorema de Pitágoras - é uma relação na geometria euclidiana entre os três lados de um triângulo (triângulo retângulo). Em termos de áreas, ele afirma:
Em qualquer triângulo retângulo, a área do quadrado cujo lado é o hipotenusa (o lado oposto ao ângulo direito) é igual à soma das áreas dos quadrados cujos lados são as duas pernas (os dois lados que se encontram em um ângulo reto).
O teorema pode ser escrita como uma equação relacionando os comprimentos dos lados a, b e c, frequentemente chamada equação de Pitágoras:
em que c representa o comprimento da hipotenusa, e a e b representam os comprimentos dos outros dois lados.
O teorema de Pitágoras é nomeado após o Matemático grego Pitágoras (cerca de 570 aC cerca de 495 aC), que por tradição é creditado com a sua descoberta e prova , embora muitas vezes é argumentou que o conhecimento do teorema anterior ele. Há evidências de que Matemáticos babilônios entendeu a fórmula, embora haja pouca evidência de sobrevivência que eles usaram em uma estrutura matemática.
O teorema tem inúmeras provas , possivelmente mais do que qualquer teorema matemático. Estes são muito diversificada, incluindo ambas as provas geométricas e algébricas provas, com alguns que remonta milhares de anos. O teorema pode ser generalizada de várias maneiras, incluindo espaços de dimensões superiores, para os espaços que não são Euclidiana, para objetos que não são triângulos retângulos e, na verdade, para objetos que não são triângulos em tudo, mas n sólidos dimensionais. O teorema de Pitágoras tem atraído o interesse fora da matemática como um símbolo da abstruseness matemática, mística, ou poder intelectual; referências populares na literatura, peças teatrais, musicais, músicas, selos e desenhos animados são abundantes.
Outras formas
Como apontado na introdução, se c denota o comprimento da hipotenusa e a e b representam os comprimentos dos outros dois lados, o teorema de Pitágoras pode ser expressa como a equação de Pitágoras:
Se o comprimento de ambos os a e b são conhecidos, c, em seguida, pode ser calculada como se segue:
Se o comprimento da hipotenusa C, e uma perna (a ou b) são conhecidos, em seguida, o comprimento da outra perna pode ser calculado com as seguintes equações:
ou
A equação de Pitágoras refere-se os lados de um triângulo de uma maneira simples, de modo que, se os comprimentos de quaisquer dois lados é conhecido o comprimento do terceiro lado pode ser encontrado. Outro corolário do teorema é que, em qualquer triângulo, a hipotenusa é maior do que qualquer uma das pernas, mas menos do que a soma dos mesmos.
A generalização deste teorema é a lei de co-senos, que permite o cálculo do comprimento do terceiro lado de qualquer triângulo, dado os comprimentos dos dois lados e o tamanho do ângulo entre elas. Se o ângulo entre os lados é um ângulo recto, a lei de co-senos reduz para a equação de Pitágoras.
Provas
Este teorema pode ter provas mais conhecidas do que qualquer outro (a lei de reciprocidade quadrática ser outro candidato para essa distinção); o livro O Pitágoras Proposição contém 370 provas.
Prova usando triângulos semelhantes
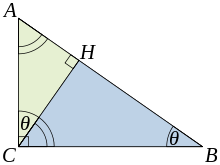
Esta prova é baseada na proporcionalidade dos lados de dois triângulos semelhantes, isto é, sobre o facto de a razão entre quaisquer dois lados correspondentes de triângulos semelhantes, é a mesma, independentemente do tamanho dos triângulos.
Vamos ABC representam um triângulo retângulo, com o ângulo certo localizada em C, como mostrado na figura. Chamamos a altitude do ponto C, e chamada H sua intersecção com o lado AB. O ponto H divide o comprimento da hipotenusa C em partes D e E. O novo triângulo é ACH semelhante ao triângulo ABC, porque ambos têm um ângulo recto (por definição da altura), e que partilham o ângulo A, o que significa que o terceiro ângulo irá ser a mesma em ambos os triângulos, bem como, como θ marcados na figura. Por um raciocínio semelhante, o triângulo CBH também é semelhante à ABC. A prova da semelhança dos triângulos requer a Triângulo postulado: a soma dos ângulos de um triângulo é dois ângulos rectos, e é equivalente à postulado paralelo. Semelhança dos triângulos leva à igualdade de proporções de cada lado correspondente:
O primeiro resultado iguala o co-seno de cada θ ângulo eo segundo resultado equivale a senos.
Estas proporções podem ser escrito como:
Somando essas duas igualdades, obtemos
que, arrumando a casa, é o teorema de Pitágoras:
O papel desta prova na história é o assunto de muita especulação. A questão subjacente é por isso que Euclides não utilizar esta prova, mas inventou outro. Uma conjectura é que a prova de triângulos semelhantes envolveu uma teoria das proporções, um tema que não foram discutidos até mais tarde no Elements, e que a teoria das proporções necessárias mais desenvolvimento naquela época.
A prova de Euclid
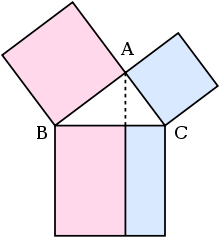
Em linhas gerais, é aqui como a prova em Euclides 's Elementos rendimentos. A grande praça é dividida em um retângulo de esquerda e direita. Um triângulo é construído que tem metade da área do retângulo esquerdo. Em seguida, outro triângulo é construído que tem metade da área da praça no lado mais à esquerda. Estes dois triângulos são mostrados para ser congruente, provando este quadrado tem a mesma área que o rectângulo da esquerda. Este argumento é seguida por uma versão semelhante para o direito e o rectângulo quadrado restante. Colocar os dois rectângulos em conjunto para reformar o quadrado da hipotenusa, a sua área é a mesma que a soma da área dos outros dois quadrados. Os detalhes são os próximos.
Sejam A, B, C ser a vértices de um triângulo retângulo, com um ângulo reto em A. Deixe cair uma perpendicular de A para o lado oposto da hipotenusa no quadrado da hipotenusa. A linha que divide o quadrado da hipotenusa em dois rectângulos, tendo cada uma a mesma área que um dos dois quadrados nos pés.
Para a prova formal, que exigem quatro elementar lemas:
- Se dois triângulos têm dois lados de um igual a dois lados do outro, cada um a cada um, e os ângulos compreendidos por esses lados iguais, então os triângulos são congruentes ( -lado-ângulo lateral).
- A área de um triângulo é metade da área de qualquer paralelogramo na mesma base e com a mesma altura.
- A área de um rectângulo é igual ao produto dos dois lados adjacentes.
- A área de um quadrado é igual ao produto de dois dos seus lados (Resulta 3).
Em seguida, cada quadrado de cima está relacionada com um triângulo congruente com outro triângulo relacionados em vez de um dos dois rectângulos tornando-se o quadrado inferior.
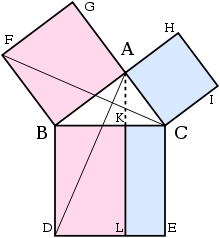
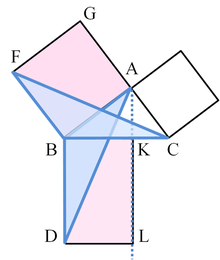
A prova é como se segue:
- Vamos ACB ser um triângulo retângulo com CAB ângulo direito.
- Em cada um dos lados BC, AB, e CA, quadrados são desenhadas, CBDE, bagf, e ACIH, nessa ordem. A construção de praças requer os teoremas imediatamente anteriores em Euclides, e depende do postulado das paralelas.
- A partir de A, desenhar uma linha paralela à BD e CE. Ele vai se cruzam perpendicularmente BC e DE no K e L, respectivamente.
- Junte-se a CF e AD, para formar o BCF triângulos e BDA.
- Ângulos CAB e BAG são os dois ângulos retos; Por conseguinte, C, A e G são colineares . Da mesma forma para a B, A, e H.
- Angles CBD e FBA são ambos ângulos retos; portanto ângulo ABD é igual ângulo FBC, já que ambos são a soma de um ângulo direito eo ângulo ABC.
- Desde AB é igual a FB e BD é igual a BC, triângulo ABD deve ser congruente ao triângulo FBC.
- Desde AKL é uma linha reta, paralela à BD, em seguida, retângulo BDLK tem o dobro da área do triângulo ABD, porque eles compartilham a base BD e têm a mesma altitude BK, ou seja, uma linha normal para a sua base comum, que liga as linhas paralelas BD e AL. (Lema 2)
- Desde C é colinear com A e G, BAGF quadrado deve ser duas vezes na área de triângulo FBC.
- Portanto BDLK retângulo deve ter a mesma área que BAGF quadrado = AB 2.
- Da mesma forma, pode-se mostrar que retângulo CKLE deve ter a mesma área que quadrado ACIH = AC 2.
- Adicionando estes dois resultados, AB 2 + 2 = AC BD × BK + KL × KC
- Desde BD = KL, BD × BK + KL × KC = BD (BK + KC) = BD × BC
- Portanto AB 2 + 2 = AC BC 2, uma vez que CBDE é um quadrado.
Esta prova, que aparece em Elementos de Euclides como a de Proposition 47 no Livro 1, demonstra que a área do quadrado da hipotenusa é igual à soma das áreas dos outros dois quadrados. Isto é bastante distinta da prova por semelhança de triângulos, que é conjecturou ser a prova de que Pitágoras usado.
Prova por rearranjo
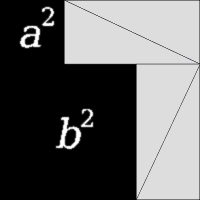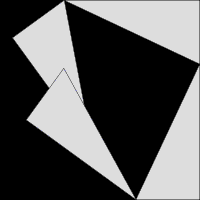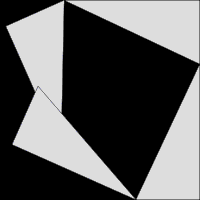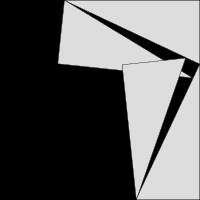
A animação da esquerda consiste em uma grande praça, lado a + b, contendo quatro triângulos retângulos idênticos. Os triângulos são mostradas em duas modalidades, a primeira das quais deixa dois quadrados a 2 e b 2 ar-livre, o segundo dos quais folhas c quadrado 2 descoberto. A área abrangida pelo quadrado exterior nunca muda, e a área dos quatro triângulos é a mesma no início e no final, de modo que as áreas pretas quadradas deve ser igual, por conseguinte, um 2 + b 2 = c 2.
A segunda prova é dada por meio da animação. A grande praça é formado com área c 2, a partir de quatro triângulos retângulos idênticos com lados a, b e c, equipados ao redor de uma pequena praça central. Em seguida, dois rectângulos são formadas com lados a e b, movendo os triângulos. Combinando o quadrado menor com esses retângulos produz dois quadrados de áreas a 2 e B 2, que devem ter a mesma área que o quadrado inicial grande.
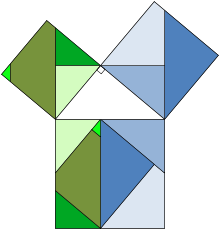
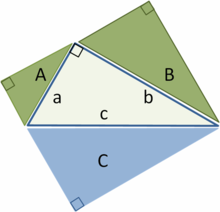
A terceira imagem, mais à direita, também dá uma prova. Os dois quadrados superiores são divididos conforme mostrado pelo sombreamento azul e verde, em pedaços que quando rearranjados podem ser feitas para se ajustar na praça inferior da hipotenusa - ou, inversamente, a grande praça pode ser dividida conforme mostrado em pedaços que enchem os outros dois . Isto mostra a área do quadrado grande que é igual a um dos dois menores.
 |  |  |
Provas algébricas
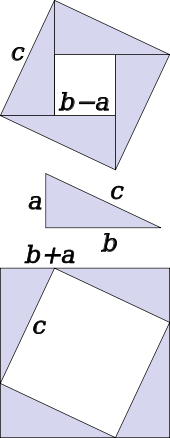
O teorema pode ser provado algebricamente usando quatro cópias de um triângulo retângulo com lados a, b e c, dispostos dentro de um quadrado com o lado c como na metade superior do diagrama. Os triângulos são semelhantes com a área 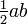 , Enquanto a pequena praça tem lado b - a área e (b - a) 2. A área da grande praça é, portanto,
, Enquanto a pequena praça tem lado b - a área e (b - a) 2. A área da grande praça é, portanto,
Mas este é um quadrado com o lado c e área de c 2, de modo
Uma prova semelhante utiliza quatro cópias do mesmo triângulo dispostas simetricamente em torno de um quadrado, com o lado c, como mostrado na parte inferior do diagrama. Isto resulta numa maior quadrado, com o lado a + b e área (a + b) 2. Os quatro triângulos e do lado quadrado c devem ter a mesma área que o quadrado maior,
dando
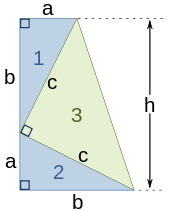
Uma prova matéria foi publicado pelo ex-presidente dos EUA, James A. Garfield . Em vez de um quadrado que utiliza um trapézio, que pode ser construído a partir do quadrado na segunda das provas acima pela bissetriz ao longo da diagonal do quadrado interior, para dar o trapezoidal, como mostrado no diagrama. O área do trapézio pode ser calculada como sendo a metade da área do quadrado, que é
A praça interior é igualmente reduzido para metade, e há apenas dois triângulos de modo a prova prossegue como acima, exceto por um fator de  , Que é removido pela multiplicação por dois para dar o resultado.
, Que é removido pela multiplicação por dois para dar o resultado.
Prova usando diferenciais
Pode-se chegar ao teorema de Pitágoras estudando como alterações em um lado produzir uma alteração na hipotenusa e empregando cálculo .
O triângulo ABC é um triângulo, como se mostra na parte superior do diagrama, com BC a hipotenusa. Ao mesmo tempo, os comprimentos são medidos triângulo como mostrado, com a hipotenusa de comprimento y, do lado CA de comprimento x e o lado AB de um comprimento de, como pode ser visto na parte inferior diagrama.
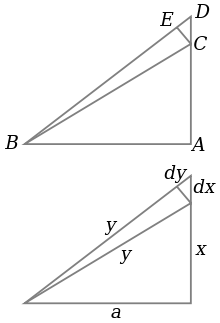
Se x é aumentado por uma quantidade pequena dx, alargando o AC lado ligeiramente para D, então y também aumenta por dy. Estes formam dois lados de um triângulo, CDE, que (com E escolhido de modo CE é perpendicular à hipotenusa) é um triângulo rectângulo aproximadamente semelhante à ABC. Por conseguinte, as proporções de seus lados deve ser o mesmo, que é:
Isto pode ser escrito como se segue:
Esta é uma equação diferencial o qual é resolvido para dar
E a constante pode ser deduzida a partir de x = 0, y = a para dar a equação
Esta é mais uma prova intuitiva do que um formal de um: ele pode ser mais rigorosos se os limites adequados são usados no lugar de dx e dy.
Conversar
O inverso do teorema também é verdadeiro:
Para todos os três números positivos a, b, e c tal que um 2 + b = 2 c 2, existe um triângulo com lados a, b e c, e cada tal triângulo tem um certo ângulo entre os lados de comprimentos a e b .
Uma declaração alternativa é:
Para qualquer triângulo com lados a, b, c, se um 2 + b = 2 c 2, então o ângulo entre a e b mede 90 °.
Este inverso também aparece em Elements de Euclides (Livro I, Proposição 48):
"Se num triângulo o quadrado de um dos lados é igual à soma dos quadrados dos outros dois lados do triângulo, então, o ângulo formado pelos dois lados restantes do triângulo está à direita."
Ele pode ser comprovado utilizando o lei de co-senos ou como se segue:
Seja ABC um triângulo com os comprimentos laterais a, b, e c, com um 2 + b 2 = c 2. Construir um segundo triângulo com lados de comprimento a e b contendo um ângulo recto. Pelo teorema de Pitágoras, segue-se que a hipotenusa deste triângulo tem comprimento c = √ um 2 + b 2, o mesmo que a hipotenusa do triângulo primeiro. Uma vez que os lados dos dois triângulos são os mesmos comprimentos a, b e c, são os triângulos congruente e devem ter os mesmos ângulos. Portanto, o ângulo entre o lado de comprimentos a e b no triângulo original é um ângulo recto.
A prova acima do inverso faz uso do próprio Teorema de Pitágoras. O inverso também pode ser comprovada sem assumir o Teorema de Pitágoras.
A corolário do inverso do teorema de Pitágoras é um meio simples de determinar se um triângulo é certo, obtuso, ou aguda, como se segue. Seja c ser escolhido para ser o mais longo dos três lados e a + b> C (caso contrário não há triângulo de acordo com a da desigualdade do triângulo). As declarações a seguir se aplicam:
- Se um 2 + b 2 = c 2, em seguida, o triângulo é certo.
- Se um 2 + b 2> c 2, em seguida, o triângulo é aguda.
- Se a <c + b 2 2 2, em seguida, o triângulo é obtuso.
Edsger Dijkstra afirmou esta proposição sobre triângulos agudas, direita e obtusos nesta língua:
- sgn (α + β - γ) = sgn (a 2 + b 2 - c 2),
onde α é o ângulo oposto ao lado A, β é o ângulo oposto ao lado b, γ é o ângulo oposto ao lado C, e é a sgn assinar função.
Conseqüências e usos do teorema
Trios pitagóricos
Um Pitágoras triplo tem três números inteiros positivos a, b, e c, de modo que um 2 + b = c 2 2. Em outras palavras, uma tripla de Pitágoras representa os comprimentos dos lados de um triângulo rectângulo, onde os três lados têm comprimentos inteiros. Evidências de monumentos megalíticos na Europa do Norte mostra que tais triplos eram conhecidos antes da descoberta da escrita. Tal triplo é comumente escrita (a, b, c). Alguns exemplos bem conhecidos são (3, 4, 5) e (5, 12, 13).
Uma primitiva de Pitágoras triplo é aquele em que a, b e c representam primos entre si (o maior divisor comum de a, b e c é 1).
O que se segue é uma lista de primitivo trios pitagóricos com valores inferiores a 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12 , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77 , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Comprimentos incomensuráveis
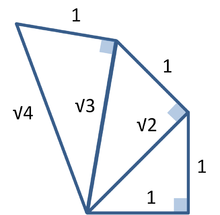
Uma das consequências do teorema de Pitágoras é que os segmentos de linha cujos comprimentos são incomensurável (por isso o rácio de que não é um número racional ) pode ser construído usando uma régua e bússola . Teorema de Pitágoras permite a construção de comprimentos incomensuráveis porque a hipotenusa de um triângulo está relacionada com os lados por a raiz quadrada operação.
A figura da direita mostra como a construção de segmentos de linha cujos comprimentos estão na relação de raiz quadrada de qualquer número inteiro positivo. Cada triângulo tem um lado (identificado como "1"), que é a unidade escolhido para a medição. Em cada triângulo retângulo, teorema de Pitágoras estabelece o comprimento da hipotenusa em termos de esta unidade. Se uma hipotenusa está relacionada com a unidade pela raiz quadrada de um número inteiro positivo que não seja um quadrado perfeito, é uma realização de um comprimento incomensurável com o aparelho, tais como √ 2, 3 √, √ 5. Para mais detalhes, consulte Quadrático irracional.
Comprimentos incomensuráveis em conflito com o conceito da escola pitagórica de números como apenas números inteiros. A escola pitagórica lidou com proporções por comparação de múltiplos inteiros de uma subunidade comum. De acordo com uma lenda, Hippasus de Metapontum (cerca de 470 aC) foi afogado no mar para dar a conhecer a existência do irracional ou incomensuráveis.
Os números complexos
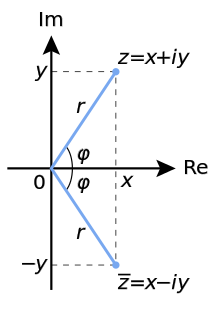
Para qualquer número complexo
o valor absoluto ou módulo é dada pela
Assim, a três quantidades, r, x e y estão relacionados pela equação de Pitágoras,
Note-se que R é definido para ser um número positivo ou zero, mas x e y pode ser negativo, bem como positivo. Geometricamente r é a distância a partir da z zero ou o ó origem no plano complexo .
Isto pode ser generalizada para encontrar a distância entre dois pontos, Z 1 e Z 2 dizer. A distância exigida é dada pelo
por isso, novamente eles estão relacionados por uma versão da equação de Pitágoras,
Distância Euclidiana em vários sistemas de coordenadas
A fórmula de distância em coordenadas cartesianas é derivado a partir do Teorema de Pitágoras. Se (x 1, y 1) e (2 x, y 2) são os pontos no plano, em seguida, a distância entre eles, também chamado o Distância euclidiana, é dada por
Mais geralmente, em euclidiana n -espaço , a distância euclidiana entre dois pontos, 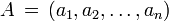 e
e 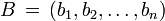 , É definido, por generalização do teorema de Pitágoras, como:
, É definido, por generalização do teorema de Pitágoras, como:
Se as coordenadas cartesianas não são usados, por exemplo, se as coordenadas polares são utilizados em duas dimensões, ou, em termos mais gerais, se coordenadas curvilíneas são usados, as fórmulas que expressam a distância Euclidiana é mais complicado do que o teorema de Pitágoras, mas pode ser derivada a partir dele. Um exemplo típico em que a distância em linha recta entre dois pontos é convertida em coordenadas curvilíneas pode ser encontrado no aplicações de polinômios de Legendre em física. As fórmulas podem ser descobertos usando o teorema de Pitágoras com as equações que relacionam as coordenadas curvilíneas para coordenadas cartesianas. Por exemplo, as coordenadas polares (r, θ) pode ser introduzido como:
Em seguida, dois pontos com locais (R1, θ 1) e (2 R, θ 2) estão separados por uma distância s:
Realizando as praças e combinando termos, a fórmula de Pitágoras para a distância em coordenadas cartesianas produz a separação em coordenadas polares como:
usando o trigonométrica fórmulas produto-a-soma. Esta fórmula é a lei dos cossenos , às vezes chamado de Generalized Teorema de Pitágoras. A partir deste resultado, para o caso em que os raios para os dois locais estão em ângulos rectos, o ângulo fechado θ Δ = π / 2, e a forma correspondente ao teorema de Pitágoras é recuperado: 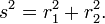 O teorema de Pitágoras, válido para triângulos retângulos, portanto, é um caso especial da lei mais geral de co-senos, válido por triângulos arbitrários.
O teorema de Pitágoras, válido para triângulos retângulos, portanto, é um caso especial da lei mais geral de co-senos, válido por triângulos arbitrários.
Fórmula fundamental da trigonometria
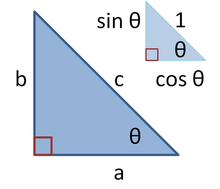
Em um triângulo retângulo com lados a, b e c hipotenusa, trigonometria determina a seno e co-seno do ângulo θ entre o lado um ea hipotenusa como:
Do que se segue:
onde a última etapa se aplica o teorema de Pitágoras. Esta relação entre seno e cosseno às vezes é chamado de fórmula fundamental da trigonometria fundamental. Em triângulos semelhantes, as proporções dos lados são iguais, independentemente do tamanho dos triângulos, e dependem dos ângulos. Consequentemente, na figura, o triângulo com hipotenusa do tamanho da unidade tem lado oposto do tamanho θ sin e lateral adjacente do tamanho cos θ em unidades da hipotenusa.
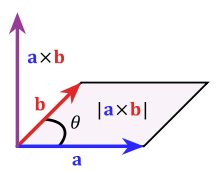
Relação com o produto cruzado
O teorema de Pitágoras relaciona o produto cruzado e produto de ponto de uma maneira semelhante:
Isto pode ser visto a partir das definições do produto cruzado e produto escalar, como
com n um vector unidade normal para ambos a e b. O relacionamento decorre destas definições ea fórmula fundamental da trigonometria.
Isto também pode ser utilizado para definir o produto cruzado. Reorganizando a seguinte equação é obtida
Esta pode ser considerada como uma condição sobre o produto de modo transversal e parte da sua definição, por exemplo, em sete dimensões.
Generalizações
Figuras semelhantes nos três lados
A generalização do teorema de Pitágoras que se estende para além das áreas de quadrados dos três lados para figuras semelhantes era conhecido por Hipócrates de Chios, no século V aC, e foi incluído por Euclides em seus elementos :
Se uma erige figuras semelhantes (ver geometria euclidiana ) com os lados correspondentes sobre os lados de um triângulo rectângulo, em seguida, a soma das áreas de os sobre os dois lados mais pequenos é igual à área da outra no lado maior.
Esta extensão assume que os lados do triângulo original são os lados correspondentes das três figuras congruentes (para os rácios comuns dos lados entre os números semelhantes são a: b:. C, enquanto prova de Euclides só é aplicado a polígono convexo, o teorema também se aplica para polígonos côncavos e até mesmo para valores semelhantes que têm limites curvos (mas ainda com a parte de estar do lado do triângulo original contorno de uma figura).
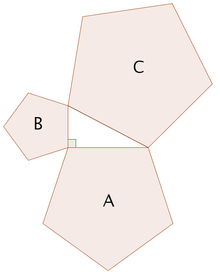
A ideia básica subjacente a esta generalização é que a área de uma figura plana é proporcional ao quadrado de qualquer dimensão linear, e em particular é proporcional ao quadrado do comprimento de qualquer lado. Assim, se os números semelhantes com as áreas A, B e C são erguidos em lados com comprimentos correspondendo a, b e c, em seguida:
Mas, pelo teorema de Pitágoras, a 2 + b 2 = c 2, então A + B = C.
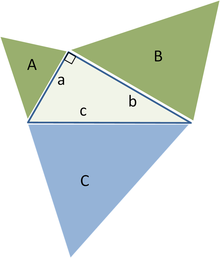
Por outro lado, se pudermos provar que A + B = C por três figuras semelhantes sem usar o teorema de Pitágoras, então nós podemos trabalhar para trás para construir uma prova do teorema. Por exemplo, o centro do triângulo de partida podem ser replicados e utilizados como um triângulo na sua hipotenusa C, e dois triângulos direitos semelhantes (A e B) construídos sobre os outros dois lados, formada pela divisão do triângulo central pela sua altitude. A soma das áreas dos dois triângulos menores, por conseguinte, é o de o terceiro, assim, A + B = C e invertendo a lógica acima conduz ao teorema de Pitágoras a 2 + 2 b = c 2.
Lei dos cossenos
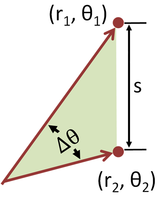
O teorema de Pitágoras é um caso especial do teorema mais geral sobre os comprimentos dos lados de qualquer triângulo, a lei dos cossenos:
onde θ é o ângulo entre os lados a e b.
Quando θ é de 90 graus, em seguida, cos θ = 0, e para a fórmula reduz o teorema de Pitágoras habitual.
Triângulo arbitrário
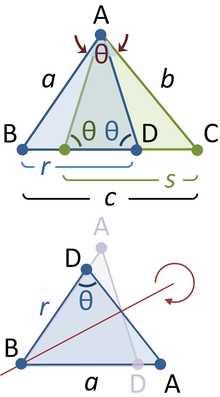
Em qualquer ângulo seleccionado de um triângulo geral de lados a, b, c, inscrever um triângulo isósceles de tal modo que os ângulos iguais na sua θ base é o mesmo que o ângulo seleccionado. Suponha que o θ ângulo selecionado fica em frente ao lado da etiqueta c. Inscrevendo o isósceles formas triângulo triângulo ABD com ângulo θ lado oposto e com um lado r juntamente c. Um segundo triângulo é formado com ângulo θ lado oposto b e um lado com comprimento ao longo s c, como mostrado na figura. Tabit ibn Qorra afirmado que os lados das três triângulos foram relacionados como:
À medida que o ângulo se aproxima de θ π / 2, a base do triângulo isósceles estreitos, e r e s comprimentos sobrepõem cada vez menos. Quando θ = π / 2, ADB torna-se um triângulo, r + s = c direito, e teorema de Pitágoras a original "se recuperou.
Uma prova observa que o triângulo ABC tem os mesmos ângulos como triângulo ABD, mas na ordem inversa. (Os dois triângulos compartilhar o ângulo no vértice B, ambos contêm a θ ângulo, e por isso também tem o mesmo terceiro ângulo pela postulado triângulo.) Consequentemente, o ABC é semelhante ao reflexo da ABD, o DBA triângulo no painel inferior. Tomando a relação de lados opostos e adjacentes a θ,
Da mesma forma, para a reflexão do outro triângulo,
Limpando frações e adicionando estas duas relações:
o resultado necessário.
Triângulos Gerais usando paralelogramos
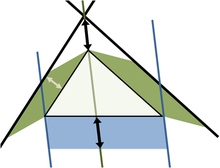
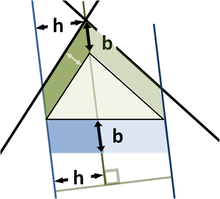
Uma outra generalização aplica-se a triângulos que não são triângulos retângulos, utilizando paralelogramos sobre os três lados no lugar de praças. (Quadrados é um caso especial, é claro.) A figura superior mostra que, para um triângulo escaleno, a área do paralelogramo do lado mais longo que representa a soma das áreas dos paralelogramos no dos outros dois lados, desde o paralelogramo na lado comprido é construído como indicado (as dimensões marcadas com setas são os mesmos, e determinar os lados do paralelogramo inferior). Esta substituição de praças com paralelogramos tem uma semelhança evidente com o teorema de Pitágoras 'original, e foi considerada uma generalização por Pappus de Alexandria, em 4 dC
A figura inferior mostra os elementos de prova. Concentre-se no lado esquerdo da figura. O paralelogramo verde à esquerda tem a mesma área que a esquerda, parte azul do paralelogramo fundo porque ambos têm a mesma base b e altura h. No entanto, o paralelogramo verde à esquerda também tem a mesma área que o paralelogramo verde à esquerda da figura superior, porque eles têm a mesma base (o lado superior esquerdo do triângulo) e da mesma altura normal para que o lado do triângulo. Repetindo o argumento para o lado direito da figura, a parte inferior do paralelogramo tem a mesma área como a soma dos dois paralelogramos verdes.
Geometria sólida
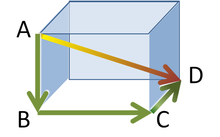
Em termos da geometria sólido, o teorema de Pitágoras pode ser aplicado a três dimensões, como se segue. Considere-se um sólido rectangular, como mostrado na figura. O comprimento da diagonal BD é encontrado a partir de teorema de Pitágoras como:
onde estes três lados formam um triângulo rectângulo. Usando BD diagonal horizontal ea aresta vertical AB, o comprimento da diagonal do AD em seguida, é encontrado por uma segunda aplicação do teorema de Pitágoras como:
ou, fazendo tudo em uma única etapa:
Este resultado é a expressão tridimensional para a magnitude de um vector v (AD diagonal) em termos dos seus componentes ortogonais {v (k} os três lados perpendiculares entre si):
Esta formulação de um só passo pode ser visto como uma generalização do teorema de Pitágoras para dimensões maiores. No entanto, este resultado é realmente apenas a aplicação repetida de teorema de Pitágoras do original "a uma sucessão de triângulos retângulos em uma seqüência de planos ortogonais.
Uma generalização substancial do teorema de Pitágoras para três dimensões é teorema de de Gua, nomeado para Jean Paul de gua de Malves: Se um tetraedro tem um canto em ângulo recto (como um canto de um cubo ), em seguida, o quadrado da área da face em frente ao canto em ângulo recto, é a soma dos quadrados das áreas da outra três faces. Este resultado pode ser generalizada como no "teorema de Pitágoras n-dimensional":
Deixarser vetores ortogonais em ℝ n. Considere o n S simplex -dimensional com vértices
. (Pense no (n - 1) simplex -dimensional com vértices
não incluindo a origem como o "hipotenusa" de S e o restante (n - 1) rostos -dimensional de S como a sua "pernas") Em seguida, o quadrado do volume da hipotenusa de S é a soma dos quadrados de a. os volumes de n pernas.
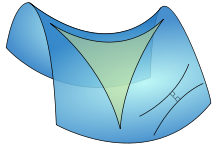
Esta afirmação é ilustrado em três dimensões por o tetraedro na figura. O "hipotenusa" é a base do tetraedro na parte de trás da figura, e as "pernas" são os três lados que emanam do vértice no primeiro plano. À medida que a profundidade da base do vértice aumenta, a área das "pernas" aumenta, enquanto que a da base é fixada. O teorema sugere que, quando esta profundidade é no valor criando um vértice direito, a generalização do teorema de Pitágoras se aplica. Em uma formulação diferente:
Dado umn-rectangularnsimplex-dimensional, o quadrado da (n- 1) -Conteúdo dafaceta opondo o vértice direito será igual à soma dos quadrados dos (n- 1) -contents das facetas restantes.
Espaços de produto interno
O teorema de Pitágoras pode ser generalizada para espaços com produto interno, que são generalizações dos 2-dimensionais e 3 dimensões familiares espaços euclidianos . Por exemplo, uma função pode ser considerado como um vector com um número infinito de componentes em um espaço interior do produto, como na análise funcional.
Num espaço interior do produto, o conceito de perpendicularidade é substituído pelo conceito de ortogonalidade: dois vectores de v e w são ortogonais se o seu produto interno 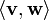 é zero. O produto interno é uma generalização do produto do ponto de vectores. O produto escalar é chamado o padrão do produto interno ou o euclidiana produto interno. No entanto, outros produtos internos são possíveis.
é zero. O produto interno é uma generalização do produto do ponto de vectores. O produto escalar é chamado o padrão do produto interno ou o euclidiana produto interno. No entanto, outros produtos internos são possíveis.
O conceito de comprimento é substituído pelo conceito danorma ||v|| de um vectorv, definida como:
Em um espaço ao produto interno, oteorema de Pitágorasafirma que para quaisquer dois vetores ortogonaisvewtemos
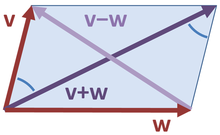
Aqui, a vectores de v e w são semelhantes para os lados de um triângulo rectângulo com hipotenusa dada pela soma vectorial v + w . Esta forma de o teorema de Pitágoras é uma consequência das propriedades do produto interno:
onde os produtos internos dos termos cruzados são iguais a zero, devido a ortogonalidade.
Uma outra generalização do teorema de Pitágoras em um espaço com produto interno aos vetores não-ortogonais, é a lei do paralelogramo:
que diz que o dobro da soma dos quadrados dos comprimentos dos lados de um paralelogramo, é a soma dos quadrados dos comprimentos das diagonais. Qualquer norma que satisfaz essa igualdade é ipso facto uma norma correspondente a um produto interno.
A identidade de Pitágoras pode ser estendido para montantes superiores a dois vectores ortogonais. Se v 1 , v 2 , ..., v n são vectores ortogonais dois a dois-em-um espaço interior do produto, então a aplicação do teorema de Pitágoras a pares sucessivos de estes vectores (como descrito para o 3-dimensões na secção relativa à geometria sólida ) resulta a equação
Identidade de Parseval é mais uma generalização que considera somas infinitas de vetores ortogonais.
Para o produto interno
(Bé umHermitianamatriz definida positiva eu *atransposta conjugada deu) o teorema de Pitágoras é:
ondePé umaprojeção que satisfaz:
O mapa linear:
em seguida, é umaprojecção ortogonal.
Euclidiana não geometria
O teorema de Pitágoras é derivado dos axiomas da geometria euclidiana , e de fato, o teorema de Pitágoras dado acima não se sustenta em uma geometria não-euclidiana. (O teorema de Pitágoras foi mostrado, de fato, para ser equivalente a paralela de Euclides (Quinta) Postulado.) Em outras palavras, em geometria não-euclidiana, a relação entre os lados de um triângulo deve necessariamente ter uma forma não-pitagórica. Por exemplo, em geometria esférica, todos os três lados do triângulo retângulo (digamos um , b , e c ) delimitam uma octant da esfera unitária têm comprimento igual a π / 2, e todos os seus ângulos são ângulos retos, o que viola o teorema de Pitágoras porque um 2 + b 2 ≠ c 2 .
Aqui dois casos de geometria não-euclidiana são considered- geometria esférica e hiperbólica geometria plana; em cada caso, tal como no caso euclidiana para triângulos não-direita, o resultado de substituir o teorema de Pitágoras segue a partir da lei apropriada de co-senos.
No entanto, o teorema de Pitágoras permanece verdadeiro em geometria e geometria hiperbólica elíptica se a condição de que o triângulo ser direita é substituído com a condição de que dois dos ângulos de sum para o terceiro, dizem Uma + B = C . Os lados são então relacionadas como se segue: a soma das áreas dos círculos com diâmetros um e b é igual à área do círculo com diâmetro c .
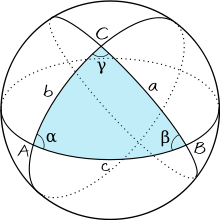
Geometria esférica
Para qualquer triângulo rectângulo sobre uma esfera de raioR(por exemplo, se γ na figura é um ângulo recto), com lados deum,b,c, a relação entre os lados tem a forma:
Esta equação pode ser derivada como um caso especial dalei esférica dos cossenos que se aplica a todos os triângulos esféricos:
Ao utilizar a série de Maclaurin para a função co-seno, de cos x ≈ 1 - x 2 / 2 , pode ser mostrado que, como o raio R se aproxima do infinito e os argumentos a / R, b / c e R / R tendem para zero, o esférica relação entre os lados de um triângulo rectângulo se aproxima da forma de teorema de Pitágoras. Substituindo o quadrática aproximada para cada um dos co-senos na relação esférica para um triângulo:
Multiplicando as quantidades entre parênteses, o teorema de Pitágoras é recuperado para grandes raios deR:
onde ostermos de ordem superiorse tornar desprezível comoRtorna-se grande.
Geometria hiperbólica
Para um triângulo retângulo em geometria hiperbólica com os ladosum,b,ce com o ladocem frente a um ângulo direito, a relação entre os lados assume a forma:
onde cosh é o co-seno hiperbólico. Esta fórmula é uma forma especial do direito hiperbólica dos cossenos que se aplica a todos os triângulos hiperbólicas:
γ com o ângulo no vértice oposto ao ladoc.
Ao utilizar asérie de Maclaurinpara o co-seno hiperbólico,coshx≈ 1 +x 2/ 2, pode ser mostrado que, como um triângulo hiperbólica torna-se muito pequeno (isto é, comoum,b, ectudo abordagem zero), a relação hiperbólica para um triângulo retângulo aborda a forma de teorema de Pitágoras.
Geometria diferencial
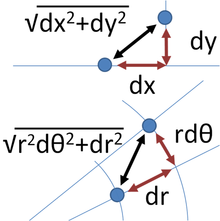
Em um nível infinitesimal, no espaço tridimensional, o teorema de Pitágoras descreve a distância entre dois pontos infinitamente separados como:
com ds o elemento de distância e ( DX , DY , DZ ) os componentes do vector que separa os dois pontos. Um tal espaço é chamado um espaço euclidiano . No entanto, uma generalização deste expressão útil para coordenadas geral (não apenas cartesiano) e espaços gerais (não apenas euclidiana) toma a forma:
onde g ij é chamado o tensor métrico. Pode ser uma função da posição. Tal espaços curvos incluem geometria Riemannianos como um exemplo geral. Esta formulação também se aplica a um espaço euclidiano ao usar coordenadas curvilíneas. Por exemplo, em coordenadas polares :
História
Há um debate se o teorema de Pitágoras foi descoberto uma vez, ou muitas vezes em muitos lugares.
A história do teorema pode ser dividido em quatro partes: conhecimento detrios pitagóricos, o conhecimento da relação entre os lados de umtriângulo retângulo, o conhecimento das relações entre ângulos adjacentes, e provas do teorema dentro de algum sistema dedutivo.
Bartel Leendert van der Waerden (1903-1996) conjecturou que trios pitagóricos foram descobertos algebricamente pelos babilônios. Escrito entre 2000 e 1786 aC, o reino médio egípcio papiro Berlim 6619 inclui um problema cuja solução é a de Pitágoras triplo 6: 8: 10, mas o problema não menciona um triângulo. O mesopotâmica tablet Plimpton 322 , escrito entre 1790 e 1750 aC, durante o reinado de Hammurabi , o Grande, contém muitas entradas estreitamente relacionadas com trios pitagóricos.
Na Índia , o Baudhayana Sulba Sutra , as datas dos quais são dados de várias formas como entre o século 8 aC eo século 2 aC, contém uma lista de trios pitagóricos descoberto algebricamente, uma declaração do teorema de Pitágoras, e uma geométrica prova da pitagórica teorema para um isósceles triângulo retângulo. O Apastamba Sulba Sutra ( ca. 600 aC) contém uma prova numérica do teorema de Pitágoras geral, usando uma computação área. Van der Waerden acreditava que "certamente foi baseado em tradições anteriores". Boyer (1991) acha que os elementos encontrados no Sulba-sũtram pode ser de derivação da Mesopotâmia.
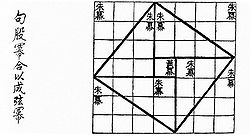
Com conteúdo conhecidos muito antes, mas em textos sobreviventes datam de aproximadamente do século I aC, o chinês texto Zhou Jing Bi Suan (周髀算经), ( A aritmética clássico da Gnomon e as circulares Paths of Heaven ) dá um raciocínio para o teorema de Pitágoras para a (3, 4, 5) triângulo na China é chamado de "Gougu Teorema" (勾股定理). Durante o Dinastia Han (202 aC a 220 dC), trios pitagóricos aparecem em Os Nove Capítulos da Matemática Art , juntamente com uma menção de triângulos retângulos. Alguns acreditam que o teorema surgiu pela primeira vez na China , onde é alternativamente conhecido como a "Shang Gao Teorema" (商高定理), em homenagem ao Duque de astrônomo e matemático de Zhou, cujo raciocínio compôs a maioria do que foi na Zhou Bi Suan Jing .
Pitágoras , cujas datas são comumente dado como 569-475 aC, usou métodos algébricos para construir trios pitagóricos, de acordo com o comentário de Proclus em Euclid . Proclus, no entanto, escreveu entre 410 e 485 dC. Conforme Sir Thomas L. Heath (1861-1940), sem atribuição específica do teorema de Pitágoras existe na literatura grega sobrevivente dos cinco séculos depois de Pitágoras viveu. No entanto, quando autores como Plutarco e Cícero atribuiu o teorema de Pitágoras, fizeram-no de uma forma que sugere que a atribuição era amplamente conhecido e inquestionável. "Se esta fórmula é justamente atribuída a Pitágoras, pessoalmente, [...] pode-se seguramente assumir que ele pertence ao período mais antigo muito de matemática de Pitágoras."
Por volta de 400 aC, de acordo com Proclus, Platão deu um método para encontrar trios pitagóricos que álgebra e geometria combinada. Cerca de 300 aC, em Euclides 's Elements , o mais velho sobrevivente prova axiomática do teorema é apresentado.
Na cultura popular
O teorema de Pitágoras surgiu nacultura popularem uma variedade de maneiras.
- Um verso dacanção de major-general naópera cômica Gilbert e Sullivan The Pirates of Penzance, "Sobre o teorema binomial eu estou cheio de um monte o 'notícia, com muitos fatos alegres sobre o quadrado da hipotenusa", faz uma oblíqua de referência com o teorema.
- O Espantalho no filme O Mágico de Oz faz uma referência mais específica para o teorema. Após receber seu diploma da Wizard, ele imediatamente exibe seu "conhecimento" por recitar uma versão mutilada e incorreto do teorema: "A soma das raízes quadradas de quaisquer dois lados de um triângulo isósceles é igual à raiz quadrada do restante lado. Oh, alegria! Oh, êxtase! Eu tenho um cérebro! "
- Em 2000, Uganda lançou uma moeda com a forma de um triângulo retângulo isósceles. A cauda do moeda tem uma imagem de Pitágoras ea equação α 2 + β 2 = γ 2 , acompanhado com a menção "Pitágoras Millennium".
 | |
- Grécia,Japão,San Marino,Serra Leoa, eSurinameemitiramselos postaisalusivos Pitágoras e do teorema de Pitágoras.
- Em Ficção especulativa de Neal Stephenson Anathem , o teorema de Pitágoras é referido como "o teorema Adrakhonic '. Uma prova geométrica do teorema é exibido ao lado de uma nave alienígena para demonstrar compreensão dos alienígenas da matemática.
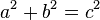
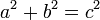
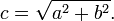
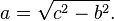
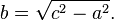
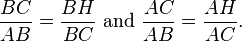
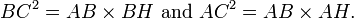
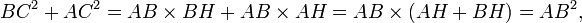
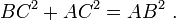
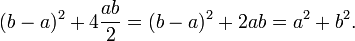
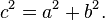
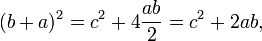
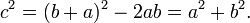
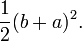
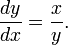
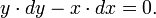
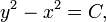
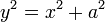
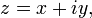
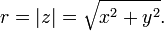
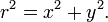
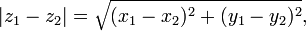
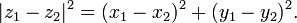
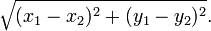
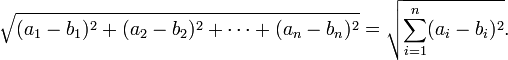
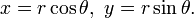
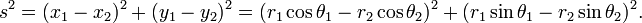
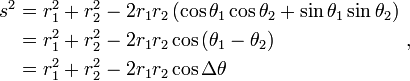
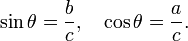
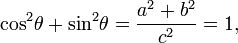
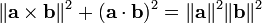
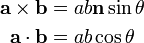
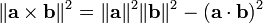
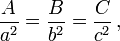
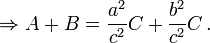
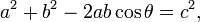
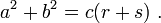
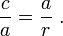
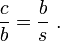
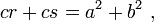

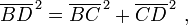
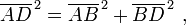
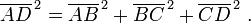
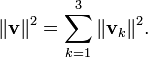
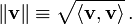
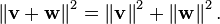
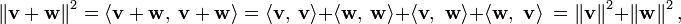
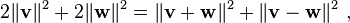
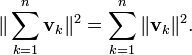
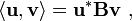
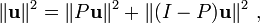
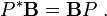
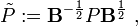
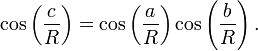
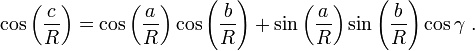
![1-\left(\frac{c}{R}\right)^2= \left[1-\left(\frac{a}{R}\right)^2 \right]\left[1-\left(\frac{b}{R}\right)^2 \right] + \ \mathrm{higher\ order\ terms}](../../images/1436/143667.png)