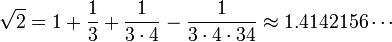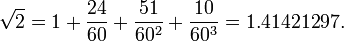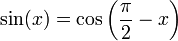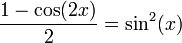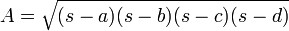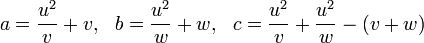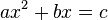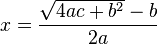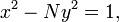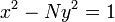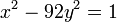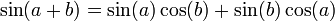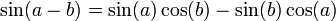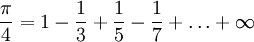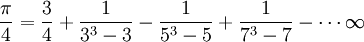Matemática indiana
Fundo para as escolas Wikipédia
Arranjar uma seleção Wikipedia para as escolas no mundo em desenvolvimento sem internet foi uma iniciativa da SOS Children. Clique aqui para saber mais sobre apadrinhamento de crianças.
| História da ciência |
|---|
 |
Fundo
|
Por época
|
Por cultura
|
Ciências Naturais
|
|
|
Ciências Sociais
|
Tecnologia
|
Medicina
|
Páginas de navegação
|
Matemática indianos -que aqui é a matemática que surgiram em Sul da Ásia desde os tempos antigos até o final do 18o século teve o seu início na Idade do Bronze da civilização do Vale do Indo (2600-1900 BCE) ea Idade do Ferro Cultura védica (1500-500 aC). No período clássico da matemática indiana ( 400 CE para 1200 CE), importantes contribuições foram feitas por estudiosos como Aryabhatta, Brahmagupta, e Bhaskara II. Matemáticos indianos fizeram contribuições iniciais para o estudo do sistema decimal número , de zero , os números negativos , aritmética e álgebra . Além disso, trigonometria , tendo evoluído no Mundo helenístico e tendo sido introduzido na antiga Índia através da tradução do grego obras, era mais avançada na Índia, e, em particular, as definições modernas de seno e co-seno foram desenvolvidos lá. Estes conceitos matemáticos foram transmitidas ao Oriente Médio , China e Europa e levou a novos desenvolvimentos que agora formam os fundamentos de muitas áreas da matemática.
Trabalhos matemáticos indianos antigos e medievais, todas compostas em sânscrito , geralmente consistia de uma seção de sutras em que um conjunto de regras ou problemas foram apresentadas com grande economia no verso, a fim de ajudar memorização por um estudante. Isto foi seguido por uma segunda secção que consiste de um comentário em prosa (às vezes vários comentários de diferentes estudiosos) que explicou o problema mais detalhadamente e apresentada uma justificação para a solução. Na seção prosa, a forma (e, portanto, sua memorização) não foi considerado tão importante quanto as idéias envolvidas. Todos os trabalhos matemáticos foram transmitidas oralmente até aproximadamente 500 aC; depois, foram transmitidos oralmente e em forma manuscrita. O documento mais antigo existente matemático produzido no subcontinente indiano é a casca de bétula Bakhshali Manuscrito, descoberto em 1881 na aldeia de Bakhshali, perto Peshawar (dia moderno Paquistão ) e é provável que a partir do século VII dC.
Um marco mais tarde na matemática indiana foi o desenvolvimento do expansões em séries de funções trigonométricas (seno, cosseno, e arcotangente) por matemáticos da Kerala escola no século XV CE. Seu trabalho notável, completou dois séculos antes da invenção do cálculo na Europa, desde o que hoje é considerado o primeiro exemplo de uma série de potência (com exceção da série geométrica). No entanto, eles não formulou uma teoria sistemática de diferenciação e integração , nem há qualquer evidência direta de seus resultados ser transmitidos fora Kerala .
Campos da matemática indiana
Algumas das áreas de matemática estudados na Índia antiga e medieval incluem o seguinte:
- Aritmética : Sistema decimal, números negativos (ver Brahmagupta), Zero (ver Hindu-arábico sistema de numeração), o moderno notação posicional sistema numeral , Números de ponto flutuante (ver Kerala Escola), Teoria dos números , a Infinity (veja Yajurveda), Números transfinitos, números irracionais (ver Sulba Sutras)
- Geometria : Raízes quadradas (ver Bakhshali aproximação), Raízes cúbicas (ver Mahavira), Trios pitagóricos (veja Sulba Sutras; Baudhayana e Apastamba estado do teorema de Pitágoras sem prova), Transformação (ver Panini), triângulo de Pascal (veja Pingala)
- Álgebra : equações quadráticas (veja Sulba Sutras, Aryabhata, e Brahmagupta), Equações cúbicas (veja Mahavira e Bhaskara), Quárticas equações (equações biquadrada, ver Mahavira e Bhaskara)
- Lógica matemática: Gramáticas formais, teoria da linguagem formal, a Panini-Backus forma (ver Panini), Recursão (veja Panini)
- Matemática Geral: números de Fibonacci (ver Pingala), primeiras formas de código Morse (veja Pingala), Logaritmos , índices (veja Jaina matemática), Algoritmos , Algorism (veja Aryabhata e Brahmagupta)
- Trigonometria : Funções trigonométricas (veja Surya Siddhanta e Aryabhata), Séries trigonométricas (veja Madhava e Kerala Escola)
Matemática indianos mostram muitas maneiras diferentes de cultura indiana.
Harappan Matemática (2600 aC - 1700 aC)
Os primeiros indícios do uso da matemática na Sul da Ásia está nas artefatos da Civilização do Vale (IVC), também chamada de civilização Harappan. Escavações em Harappa, Mohenjo-daro (Paquistão) e outros locais do rio Indus vale descobriram evidências do uso da matemática prática. As pessoas do IVC fabricados tijolos cujas dimensões eram na proporção 4: 2: 1, considerado favorável para a estabilidade de uma estrutura de tijolos. Eles usaram um sistema padronizado de pesos com base nas proporções: 20/1, 10/1, 1/5, 1/2, 1, 2, 5, 10, 20, 50, 100, 200 e 500, com a unidade peso igual a cerca de 28 gramas (e aproximadamente igual à onça Inglês ou uncia grego). Eles produzido em massa em pesos regulares geométricas formas, que incluiu hexaedros, barris, cones, e cilindros, demonstrando, assim, conhecimento básico de geometria .
Os habitantes da civilização Indus também tentou padronizar a medida do comprimento a um alto grau de precisão. Eles projetaram um -cuja unidade governante-a Mohenjo-daro governante de comprimento (cerca de 1,32 polegadas ou 3,4 centímetros) foi dividido em dez partes iguais. Tijolos fabricados na antiga Mohenjo-daro, muitas vezes tinha dimensões que eram múltiplos inteiros desta unidade de comprimento.
A Tradição Oral Matemática
Matemáticos da antiga Índia e no início medieval eram quase todos sânscrito pandits (Pandita "aprendeu homens"), que foram treinados no idioma sânscrito e literatura, e possuía "um fundo comum de conhecimentos em gramática ( Vyakarana), exegese ( mimamsa) e lógica ( Nyāya). "Memorização de" o que é ouvido "( śruti em sânscrito) através de recitação desempenhou um papel importante na transmissão de textos sagrados na Índia antiga. Memorização e recitação também foi usado para transmitir obras filosóficas e literárias, bem como tratados sobre ritual e gramática. Os estudiosos modernos da Índia antiga notaram as "realizações verdadeiramente notáveis dos pandits indianos, que têm preservado enormemente textos volumosos oralmente por milênios."
Estilos de Memorização
Prodigous energia foi despendida pela antiga cultura indiana na garantia de que esses textos foram transmitidos de geração em geração com fidelidade excessiva. Por exemplo, a memorização do sagrado Vedas incluído até onze formas de recitação do mesmo texto. Os textos foram posteriormente "prova-leitura" ao comparar as diferentes versões recitado. Formas de recitação incluiu a JATA-patha (literalmente "recitação malha"), no qual a cada duas palavras adjacentes no texto foram recitados pela primeira vez na sua ordem original, em seguida, repetido na ordem inversa e, finalmente, repetido novamente na ordem original. A recitação procedeu, assim, como:
Em uma outra forma de recitação, dvaja-patha (literalmente "recitação flag") uma seqüência de N palavras foram recitados (e memorizado), emparelhando os dois primeiros e últimos dois palavras e, em seguida, procedendo como:
A forma mais complexa de recitação, ghana-patha (literalmente "recitação densa"), de acordo com (. Filliozat 2004, p 139), tomou a forma:
Que estes métodos têm sido eficazes, é testemunhado pela preservação dos mais antigo texto religioso indiano, o Rgveda ( ca. 1500 BCE), como um texto único, sem quaisquer leituras variantes. Métodos semelhantes foram usadas para memorizar textos matemáticos, cuja transmissão exclusivamente oral permaneceu até ao final do Período védico (cerca de 500 aC).
O Sutra Gênero
Atividade matemática na antiga Índia começou como uma parte de uma "reflexão metodológica" na sagrada Vedas, que tomou a forma de obras chamado Vedangas, ou, "Auxiliares do Veda" (7o-4a século aC). A necessidade de conservar o som do texto sagrado por uso de Siksa ( fonética) e (Chandas métricas); para conservar o seu significado por utilização de Vyakarana ( gramática) e Nirukta ( etimologia); e para executar corretamente os ritos no momento correto pelo uso de kalpa ( ritual) e Jyotisa ( astronomia ), deu origem aos seis disciplinas do Vedangas. Matemática surgiu como parte da últimos dois disciplinas, ritual e astronomia (que incluiu também a astrologia). Desde o Vedangas imediatamente precedeu o uso da escrita na Índia antiga, eles formaram o último da literatura exclusivamente oral. Eles foram expressas numa forma altamente comprimido acelerador, o sūtra (literalmente, "thread"):
Os conhecedores do sutra conhecê-la como tendo alguns fonemas, sendo desprovido de ambiguidade, contendo a essência, de frente para tudo, estar sem pausa e irrepreensível.
Brevidade extrema foi conseguido através de vários meios, que incluíram usando reticências "além da tolerância de linguagem natural", usando nomes técnicos em vez de nomes mais descritivos, cerceando listas mencionando apenas o primeiro eo últimas entradas, e utilizando marcadores e variáveis. Os sūtras criar a impressão de que a comunicação através do texto era "apenas uma parte de toda a instrução. O resto da instrução deve ter sido transmitido pela chamada Parampara Guru-shishya, 'sucessão ininterrupta de professor (guru) para o aluno (sisya),' e não foi aberto ao público em geral "e talvez até mesmo mantido em segredo. A brevidade alcançado em um sutra é demonstrado no seguinte exemplo de o Baudhayana Sulba Sūtra (700 aC).
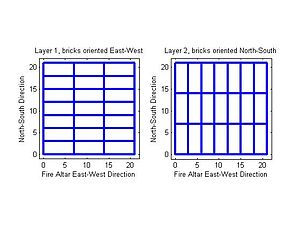
O fogo-altar doméstico no Período védico foi exigido pelo ritual para ter uma base quadrada e ser constituído de cinco camadas de tijolos com 21 tijolos em cada camada. Um método de construção de altar foi dividir um lado do quadrado em três partes iguais, usando um cabo ou corda, para dividir o lado transversal (ou perpendicular) lateral em sete partes iguais, e assim, subdividir o quadrado 21 em rectângulos congruentes . Os tijolos foram então concebidos para ser da forma do componente de rectângulo e a camada foi criado. Para formar a camada seguinte, a mesma fórmula foi usado, mas os tijolos foram dispostos transversalmente. O processo foi então repetido mais três vezes (com as direcções alternadas), a fim de completar a construção. No Baudhayana Sulba sutra, esse procedimento é descrito nas seguintes palavras:
"II.64. Depois de dividir o quadri-lateral em sete, uma transversal divide o [cabo] em três.
II.65. Em uma outra camada coloca o [tijolos] norte-apontando. "
De acordo com (Filliozat 2004, p. 144), o oficiante construir o altar tem apenas algumas ferramentas e materiais à sua disposição: um cabo (. Sânscrito, Rajju, f), dois pinos (. Sânscrito, Sanku, m), e barro para fazer tijolos (sânscrito, iṣṭakā, f.). Concisão é alcançado no Sutra, por não mencionar explicitamente o que o adjetivo "transversal" qualifica; no entanto, a partir da forma feminina do (sânscrito) adjetivo usado, é facilmente inferida para se qualificar "cordão". Da mesma forma, na segunda estrofe, "tijolos" não são explicitamente mencionados, mas inferida novamente pela forma plural feminino de "Norte-apontando." Finalmente, a primeira estrofe, diz não explicitamente que a primeira camada de tijolos são orientados na direção leste-oeste, mas que também está implícito na menção explícita de "Norte-apontando" na segunda estrofe; pois, se a orientação era para ser a mesma nas duas camadas, seria ou não ser mencionado em todos ou ser apenas mencionou na primeira estrofe. Todas estas inferências são feitas pelo oficiante como ele recorda a fórmula de sua memória.
Período Védica (1500 aC - 400 aC)
Os textos religiosos do Período Védica fornecem evidência para o uso de grandes números. Até o momento da última Veda, o Yajurvedasaṃhitā (1200-900 aC), números tão elevados como 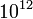 estavam a ser incluído nos textos. Por exemplo, a mantra (fórmula sacrificial) no final do annahoma ("food-oferta rito") realizada durante o Asvamedha ("sacrifício de cavalo"), e proferiu apenas antes-, during-, e logo após o nascer do sol, invoca potências de dez de uma centena de um trilhão:
estavam a ser incluído nos textos. Por exemplo, a mantra (fórmula sacrificial) no final do annahoma ("food-oferta rito") realizada durante o Asvamedha ("sacrifício de cavalo"), e proferiu apenas antes-, during-, e logo após o nascer do sol, invoca potências de dez de uma centena de um trilhão:
"Hail to SATA (" cem ",
), O granizo para sahasra ("mil"
), O granizo para ayuta ("dez mil",
), O granizo para niyuta ("centenas de milhares"
), O granizo para prayuta ("milhões"
), O granizo para Arbuda ("dez milhões,"
), O granizo para nyarbuda ("centenas de milhões",
), O granizo para Samudra ("bilhões"
, Literalmente "o mar"), o granizo para Madhya ("dez bilhões,"
, Literalmente "meio"), o granizo a anta ("centenas de bilhões",
, Lit., "fim"), o granizo para parārdha ("one trillion,"
lit., "para além de partes"), granizo ao amanhecer (USAS), saraiva ao crepúsculo (vyuṣṭi), granizo ao que vai subir (udeṣyat), granizo à que está a aumentar (udyat), granizo à que acaba ressuscitado (Udita), saraiva ao céu (svarga), granizo para o mundo (loka), granizo para todos ".
O Satapatha Brahmana (BCE século 9) contém regras para construções geométricas rituais que são semelhantes aos Sutras Sulba.
Sulba Sūtras
O Sulba sutras (literalmente, "Aforismos dos acordes" na Sânscrito védico) (c. 700-400 aC regras de lista) para a construção de altares de fogo de sacrifício. A maioria dos problemas matemáticos considerados na primavera Sulba Sūtras de "uma única exigência teológica", que de construção de altares de fogo que têm diferentes formas, mas ocupam a mesma área. Os altares foram obrigado a ser construído de cinco camadas de tijolo queimado, ainda com a condição de que cada camada consistem em 200 tijolos e que não há duas camadas adjacentes têm acordos congruentes de tijolos.
De acordo com (Hayashi 2005, p. 363), os sutras Sulba conter "a expressão verbal existente mais antiga do Teorema de Pitágoras no mundo, embora já tivesse sido conhecido para o Babilônios velho ".
A corda diagonal (akṣṇayā-Rajju) de um oblongo (retângulo) produz tanto que o flanco (pārśvamāni) ea horizontal (tiryaṇmānī)
produzir separadamente. "
Desde a declaração é um sutra, é necessariamente comprimido e que as cordas produzir não é elaborada, mas o contexto implica claramente as áreas quadrados construídos em seus comprimentos, e teria sido explicado até pelo professor para o aluno.
Eles contêm listas de Trios pitagóricos, que são casos particulares de Equações diofantinas. Eles também contêm afirmações (que com retrospectiva que sabemos ser aproximado) sobre quadratura do círculo e "circundando a praça."
Baudhayana (. C século 8 AEC) compôs a Baudhayana Sulba Sutra, o mais conhecido Sulba Sutra, que contém exemplos de trios pitagóricos simples, tais como: 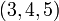 ,
, 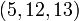 ,
, 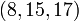 ,
, 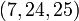 E
E 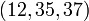 bem como uma declaração do teorema de Pitágoras para os lados de um quadrado: "A corda que é esticada em toda a diagonal de um quadrado produz uma área duas vezes o tamanho da praça original". Ele também contém a instrução geral do teorema de Pitágoras (para os lados de um rectângulo): "A corda esticada ao longo do comprimento da diagonal do rectângulo uma zona que faz um dos lados verticais e horizontais fazem em conjunto." Baudhayana dá uma fórmula para o raiz quadrada de dois,
bem como uma declaração do teorema de Pitágoras para os lados de um quadrado: "A corda que é esticada em toda a diagonal de um quadrado produz uma área duas vezes o tamanho da praça original". Ele também contém a instrução geral do teorema de Pitágoras (para os lados de um rectângulo): "A corda esticada ao longo do comprimento da diagonal do rectângulo uma zona que faz um dos lados verticais e horizontais fazem em conjunto." Baudhayana dá uma fórmula para o raiz quadrada de dois,
A fórmula é preciso até cinco casas decimais, sendo o valor verdadeiro 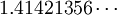 Esta fórmula é semelhante em estrutura à fórmula encontrada em um tablet da Mesopotâmia a partir do período babilônico antigo (1900-1600 BCE):
Esta fórmula é semelhante em estrutura à fórmula encontrada em um tablet da Mesopotâmia a partir do período babilônico antigo (1900-1600 BCE):
que expressa 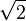 no sistema sexagesimal, e que também é preciso até cinco casas decimais (após arredondamento).
no sistema sexagesimal, e que também é preciso até cinco casas decimais (após arredondamento).
De acordo com o matemático SG Dani, a tábua cuneiforme babilônico Ca. Plimpton 322 escrita 1850 AEC "contém quinze trios pitagóricos com bastante grandes entradas, incluindo (13500, 12709, 18541), que é um triplo primitivo, indicando, em particular, que havia sofisticada compreensão sobre o tema" na Mesopotâmia em 1850 AEC. "Uma vez que estes comprimidos são anteriores ao período Sulbasutras por vários séculos, tendo em conta o aspecto contextual de algumas das triplos, é razoável esperar que a compreensão semelhante teria sido lá na Índia." Dani continua a dizer:
"Como o principal objetivo do Sulvasutras foi descrever as construções de altares e os princípios geométricos envolvidos neles, objecto de trios pitagóricos, mesmo se tivesse sido bem entendido pode ainda não ter apresentado no Sulvasutras. A ocorrência dos triplos no Sulvasutras é comparável à matemática que se pode encontrar em um livro introdutório sobre arquitetura ou de outra área aplicada semelhante, e não correspondem diretamente para o conhecimento geral sobre o tema nesse momento. Uma vez que, infelizmente, não há outras fontes contemporâneas foram encontrados isso pode nunca ser possível resolver este problema de forma satisfatória. "
Em todos os três Sutras Sulba foram compostas. Os dois restantes, o Manava Sulba Sutra composta por Manava (fl. 750-650 aC) eo Apastamba Sulba Sutra, composto por Apastamba (c. 600 aC), continha resultados semelhantes ao Baudhayana Sulba Sutra.
- Vyakarana
Um marco importante do período védico foi o trabalho de Gramático sânscrito, Pāṇini (c. 520-460 aC). Sua gramática inclui o uso precoce de lógica booleana , da operador nulo, e de gramáticas livres de contexto, e inclui um precursor do Formulário Backus-Naur (usado na descrição linguagens de programação ).
Jaina Matemática (400 aC - 200 dC)
Embora Jainismo como uma religião e filosofia antecede o seu mais famoso expoente, Mahavira ( Século 6 aC), que foi contemporâneo de Gautama Buddha , a maioria dos textos sobre Jaina topcs matemáticos foram feitos após o BCE século 6. Matemáticos Jaina são importantes historicamente como ligações cruciais entre a matemática do período védico e que do "período clássico".
A contribuição histórica significativa de Jaina matemáticos estava em sua liberando matemática indígenas de suas restrições religiosas e rituais. Em particular, o seu fascínio com a enumeração dos números muito grandes e infinitos , levou-os para classificar os números em três classes: enumeráveis, inumeráveis e infinito. Não contente com um simples noção de infinito, que passou a definir cinco diferentes tipos de infinito: o infinito em uma direção, o infinito em duas direções, o infinito na área, o infinito em todos os lugares, eo infinito perpetuamente. Além disso, os matemáticos Jaina concebido notações para poderes simples (e expoentes) de números como quadrados e cubos, o que lhes permitiu definir simples equações algébricas (beezganit samikaran). Matemáticos Jaina foram, aparentemente, também o primeiro a usar a palavra shunya (literalmente vazio em sânscrito ) para se referir a zero. Mais de um milênio depois, sua denominação tornou-se o Inglês palavra "zero" depois de uma viagem tortuosa de traduções e transliterações da Índia para a Europa. (Veja Zero: Etimologia .)
Além de Surya Prajnapti, importante Jaina obras em matemática incluiu a Vaishali Ganit (c BCE terceiro século.); o Sthananga Sutra (fl 300 aC - 200 dC.); o Anoyogdwar Sutra (fl 200 aC - 100 dC.); eo Satkhandagama (c. século 2 dC). Importantes matemáticos Jaina incluído Bhadrabahu (d 298 aC.), O autor de duas obras astronômicas, o Bhadrabahavi-Samhita e um comentário sobre a Surya Prajinapti; Yativrisham Acharya (c 176 aC.), Autor de um texto matemático chamado Tiloyapannati; e Umasvati (c. 150 aC), que, embora mais conhecido por seus escritos influentes na filosofia e Jaina metafísica, compôs um trabalho matemático chamado Tattwarthadhigama-Sutra Bhashya.
- Pingala
Entre outros estudiosos deste período que contribuíram para a matemática, o mais notável é Pingala (Pingala) ( fl. 300-200 aC), um teórico musical que foi o autor do Chandas Shastra (chandaḥ-śāstra, também Chandas Sutra chandaḥ-sutra), um sânscrito tratado sobre prosódia. Há evidências de que em seu trabalho sobre a enumeração de combinações silábicas, Pingala tropeçou em tanto o triângulo de Pascal e coeficientes binomiais , embora ele não tinha conhecimento do Próprio teorema binominal. A obra de Pingala também contém as idéias básicas de números de Fibonacci (chamados maatraameru). Embora o sutra Chandah não sobreviveu em sua totalidade, um comentário do século 10 sobre ele por Halayudha tem. Halayudha, que refere-se ao triângulo Pascal como Meru-prastāra (literalmente "a escada para Mount Meru "), tem a dizer:
"Desenhe um quadrado Começando pela metade do quadrado, desenhe duas outras praças semelhantes abaixo dela;. Abaixo desses dois, três outras praças, e assim por diante A marcação deve ser iniciado por colocar um no primeiro quadrado Coloque um em cada um dos.. dois quadrados de segunda linha. Na terceira linha em colocar um dos dois quadrados nas extremidades e, no quadrado do meio, a soma dos dígitos nos dois quadrados encontram-se acima dele. Na quarta linha colocar um dos dois quadrados nas extremidades. Em média os colocar a soma dos dígitos nos dois quadrados acima de cada. proceder desta forma. destas linhas, a segunda dá as combinações com uma sílaba, a terceira as combinações com duas sílabas, ... "
O texto também indica que Pingala estava ciente da combinatória identidade:
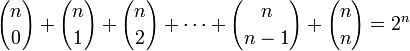
- Katyayana
Apesar de não ser um matemático Jaina, Katyayana (c. 3 século aC) é notável por ser o último dos matemáticos védicos. Ele escreveu o Katyayana Sulba Sutra, que apresentou muita geometria , incluindo o general teorema de Pitágoras e um cálculo da raiz quadrada de 2 correta a cinco casas decimais.
A tradição escrita: Comentário Prosa
Com a crescente complexidade da matemática e outras ciências exatas, eram obrigados escrita e cálculo. Consequentemente, muitos trabalhos matemáticos começou a ser escrito em manuscritos que foram, em seguida, copiados e re-copiadas de geração em geração.
"A Índia hoje é estimado para ter cerca de trinta milhões de manuscritos, o maior corpo de material de leitura, escrita à mão em qualquer lugar do mundo. A cultura letrada da ciência indiana remonta pelo menos ao século V aC ... como é demonstrado pelos elementos da Mesopotâmia literatura e astronomia presságio que entrou na Índia naquela época e (foram) definitivamente não ... preservados por via oral. "
O mais antigo comentário prosa matemática foi que no trabalho, Aryabhatiya (escrito 499 dC), um trabalho sobre astronomia e matemática. A parte matemática do Aryabhatiya foi composta de 33 sūtras (em forma de verso) que consistem em declarações matemáticas ou regras, mas sem quaisquer provas. No entanto, de acordo com (Hayashi 2003, p. 123), "isso não significa necessariamente que os seus autores não prová-los. Foi provavelmente uma questão de estilo de exposição." Desde o tempo de Bhaskara I (600 dC em diante), comentários de prosa cada vez mais começou a incluir algumas derivações (upapatti). O comentário de Bhaskara I no Aryabhatiya, tinha a seguinte estrutura:
- Regra ('sutra') no versículo por Aryabhata
- Comentário por Bhaskara I, que consiste em:
- Elucidação de regras (derivações ainda eram raros na época, mas se tornou mais comum depois)
- Exemplo (uddeśaka) geralmente em versos.
- Configuração (Nyasa / sthapana) dos dados numéricos.
- Trabalho (karana) da solução.
- Verificação (pratyayakaraṇa, literalmente "para fazer convicção") da resposta. Estes tornaram-se raros Até o século 13, derivações ou provas sendo favorecido pelo então.
Normalmente, para qualquer tópico matemático, os estudantes na Índia antiga primeiro memorizado os sutras, que, como explicado anteriormente, foram "deliberadamente inadequada" em detalhes explicativos (a fim de transmitir sucintamente as regras matemáticas bare-ossos). Os alunos, em seguida, trabalhou com os temas do comentário prosa por escrito (e desenhar diagramas) sobre-negro e poeira-boards (ou seja, placas cobertas com pó). Esta última actividade, um grampo de trabalho matemático, foi mais tarde pronta matemático-astrônomo, Brahmagupta ( fl. Sétimo século EC), para caracterizar cálculos astronômicos como "trabalho pó" (sânscrito: dhulikarman).
Numerais e do sistema de numeração decimal
O mais antigo existente script usado na Índia foi a Roteiro Kharosthi utilizado no Gandhara cultura do noroeste. Pensa-se ser de Origem aramaica e ela estava em uso desde o século IV aC ao século IV dC. Quase simultaneamente, um outro script, o Brahmi, apareceu em grande parte do sub-continente, e mais tarde se tornaria a base de muitos scripts da Ásia do Sul e Sudeste Asiático. Ambos os scripts tinha símbolos numéricos e sistemas numerais, que inicialmente não foram baseadas em um sistema de valor local. A primeira evidência datable da utilização do sistema de valor decimal na Índia é encontrado no Yavanajātaka ( ca. 270 CE) do Sphujidhvaja, uma versificação de um anterior (cerca de 150 dC) adaptação prosa indiano de uma obra perdida da astrologia helenística.
Bakhshali Manuscrito
O mais antigo manuscrito matemática existente no Sul da Ásia é a Bakhshali Manuscrito, uma casca de bétula manuscrito escrito em "híbrido budista sânscrita" no roteiro Sarada, que foi utilizado na região noroeste do subcontinente indiano entre os séculos 8 e 12 EC. O manuscrito foi descoberto em 1881 por um agricultor ao escavar em um gabinete de pedra na aldeia de Bakhshali, perto Peshawar (então em Índia britânica e agora no Paquistão ). De autoria desconhecida e agora preservado no Biblioteca Bodleian, em Oxford University , o manuscrito foi por diversas vezes com data tão cedo como os "primeiros séculos da era cristã" e tão tarde quanto entre os dias 9 e 12 º século CE. A CE século 7 é considerado agora uma data plausível, embora com a probabilidade de que o "manuscrito em sua forma atual constitui um comentário ou uma cópia de um trabalho matemático anterior."
O manuscrito sobrevivente tem setenta folhas, alguns dos quais estão em fragmentos. Seu conteúdo matemático consiste em regras e exemplos, escritos em verso, juntamente com comentários em prosa, que incluem soluções para os exemplos. Os temas tratados incluem aritméticas (fracções, raízes quadradas, lucros e perdas, juros simples, os regra de três, e regula falsi) e álgebra (simultânea equações lineares e equações de segundo grau ), e progressões aritméticas. Além disso, há um pequeno número de problemas geométricos (incluindo problemas sobre volumes de sólidos irregulares). O manuscrito Bakhshali também "emprega um sistema de valores casa decimal com um ponto para zero." Muitos dos problemas são os chamados problemas de compensação que conduzem a sistemas de equações lineares. Um exemplo de Fragmento III-5-3v é o seguinte:
"Um comerciante tem sete cavalos asava, uma segunda tem nove cavalos haya, e um terceiro tem dez camelos. Eles são igualmente bem fora no valor dos animais se dá cada dois animais, um para cada um dos outros. Encontre o preço do cada animal eo valor total para os animais possuídos por cada comerciante ".
O comentário prosa que acompanha o exemplo resolve o problema, convertendo-a três (sub-determinado) equações em quatro incógnitas e assumindo que os preços são todos os inteiros.
Período Clássico (400 - 1200)
Este período é muitas vezes conhecida como a idade de ouro da Índia Matemática. Este período viu matemáticos como Aryabhata, Varahamihira, Brahmagupta, Bhaskara I, Mahavira, e Bhaskara II dar forma mais ampla e clara para muitos ramos da matemática. Suas contribuições iria se espalhar para Ásia , o Oriente Médio , e, eventualmente, para a Europa . Ao contrário de matemática védica, seus trabalhos incluíram tanto contribuições astronômicos e matemáticos. Na verdade, a matemática desse período foi incluído na "ciência astral '(jyotiḥśāstra) e consistiu em três sub-disciplinas: ciências matemáticas (Ganita ou tantra), astrologia horóscopo (Hora ou jātaka) e adivinhação (samhita). Esta divisão em três partes é vista em Varahamihira do século VI compilation- Pancasiddhantika (literalmente panca, "cinco", Siddhanta, "conclusão de deliberação", datada 575 CE) -de cinco obras anteriores, Surya Siddhanta, Romaka Siddhanta, Paulisa Siddhanta, Vasishtha e Siddhanta Paitamaha Siddhanta, que eram adaptações de obras ainda anteriores da astronomia da Mesopotâmia, gregos, egípcios, romanos e indianos. Como explicado anteriormente, os textos principais foram compostas em sânscrito verso, e foram seguidos por comentários em prosa.
Quinta e Sexta Séculos
- Surya Siddhanta
Apesar de sua autoria é desconhecida, o Surya Siddhânta (c. 400) contém as raízes da moderna trigonometria . Alguns autores consideram que a sua foi escrito sob a influência da Mesopotâmia e na Grécia. Mas de acordo com Flavius Filostratus registra Pitágoras no século 5 aC e Apolônio de Tiana, no século 1 dC foi estudar em India.Furthermore não há provas concretas para provar que os matemáticos gregos tiveram forte influência na astronomia grega.
Este texto antigo usa a seguinte como funções trigonométricas para a primeira vez:
- Sine (Jya).
- Cosine (kojya).
- Seno inverso (Otkram jya).
Ele também contém os primeiros usos de:
- Tangent .
- Secante.
- Os ciclos de tempo cosmológicas hindus explicado no texto, que foi copiado de um trabalho anterior, dá:
- A duração média do ano sideral como 365.2563627 dias, que é apenas 1,4 segundos a mais do que o valor moderno de 365,2563627 dia.
- A duração média do ano tropical como 365.2421756 dias, que é apenas dois segundo mais curto do que o valor moderno de 365,2421988 dia.
Mais tarde matemáticos indianos como Aryabhata fez referências a este texto, enquanto posteriores árabes e latino- traduções foram muito influentes na Europa e no Oriente Médio.
- Calendário Chhedi
Este calendário Chhedi (594) contém um uso precoce do moderno lugar-valor Hindu-arábico sistema numeral agora usado universalmente (ver também Algarismos hindu-arábicos).
- Aryabhata I
Aryabhata (476-550) escreveu o Aryabhatiya. Ele descreveu os princípios fundamentais importantes da matemática em 332 shlokas. O tratado continha:
- Equações de segundo grau
- Trigonometria
- O valor de π , correta para 4 casas decimais.
Aryabhata também escreveu o Arya Siddhanta, que agora está perdido. As contribuições de Aryabhata incluem:
Trigonometria:
- Introduziu as funções trigonométricas .
- Definido o seno (jya) como a relação moderna entre meia ângulo e metade de um acorde.
- Definido o co-seno (kojya).
- Definido o versine (ukramajya).
- Definido o seno inverso (otkram jya).
- Deu métodos de cálculo dos seus valores numéricos aproximados.
- Contém as primeiras tabelas de valores de seno, cosseno e versine, em 3,75 ° intervalos de 0 ° a 90 °, com 4 casas decimais de precisão.
- Contém o pecado trigonométricas fórmula (n + 1) x - sin nx = sin nx - pecado (n - 1) x - (1/225) nx pecado.
- Trigonometria esférica.
Aritmética:
- Frações contínuas.
Álgebra:
- Soluções de equações simultâneas.
- Soluções de números inteiros de equações lineares por um método equivalente ao método moderno.
- Solução geral da equação linear indeterminado.
Astronomia matemática:
- Proposto pela primeira vez, um heliocéntrica sistema solar com as planetas girando sobre o seu eixos e na sequência de uma elíptica órbita em torno do Sol
- Cálculos precisos para constantes astronômicas, como a:
- Eclipse solar .
- Eclipse lunar .
- A fórmula para a soma do cubos, o que foi um passo importante no desenvolvimento do cálculo integral.
Cálculo:
- Infinitesimais:
- No curso de desenvolvimento de um mapeamento preciso do eclipse lunar, Aryabhatta foi obrigado a introduzir o conceito de infinitesimais (tatkalika Gati) para designar o movimento instantâneo perto da lua.
- Equações diferenciais:
- Ele expressou o movimento instantâneo perto da lua na forma de uma equação diferencial de base.
- Função exponencial:
- Ele usou afunção exponencial eem sua equação diferencial do movimento instantâneo perto da lua.
- Varahamihira
Varahamihira (505-587) produziu o Pancha Siddhanta ( Os Cinco Cânones astronómicas ). Ele fez importantes contribuições para a trigonometria , incluindo seno e cosseno mesas para quatro casas decimais de precisão e as seguintes fórmulas relativas seno e co-seno funções:
Séculos sétimo e oitavo
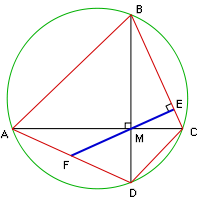
No século VII, dois campos separados, aritmética (que incluiu mensuração ) e álgebra , começaram a surgir em matemática indianos. Os dois campos mais tarde seria chamado Pati-Ganita (literalmente "matemática de algoritmos") e bīja-Ganita (lit. "matemática de sementes", com "sementes", como as sementes de plantas-representando incógnitas com o potencial de gerar, neste caso, as soluções de equações). Brahmagupta, em seu trabalho astronômico Brahma Sphuṭa siddhanta (628 CE), incluiu dois capítulos (12 e 18) dedicados a estes campos. Capítulo 12, que contém 66 versos em sânscrito, foi dividido em duas seções: "operações básicas" (incluindo raízes cúbicas, frações, razão e proporção, e permutas) e "matemática prática" (incluindo mistura, série matemática, figuras planas, tijolos empilhamento, serragem de madeira, e empilhando de grãos). Na última seção, ele declarou seu famoso teorema sobre as diagonais de um quadrilátero cíclico:
O teorema de Brahmagupta:Se umquadrilátero cíclico tem diagonais que sãoperpendiculares um ao outro, em seguida, a linha perpendicular traçada a partir do ponto de intersecção das diagonais para qualquer lado do quadrilátero sempre corta o lado oposto.
Capítulo 12 também inclui uma fórmula para a área de um quadrilátero cíclico (uma generalização dafórmula de Heron), bem como uma descrição completa dostriângulos racional (isto é,os lados com triângulos racionais e áreas racionais).
A fórmula de Brahmagupta:A área,uma, de umquadrilátero cíclico com lados de comprimentode um,b,c,d, respectivamente, é dada pela
ondeé, osemiperimeter, dada por: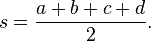
Teorema de Brahmagupta em triângulos racionais:Um triângulo com lados racionais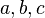 e área racional é da forma:
e área racional é da forma:
para alguns números racionais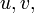 e
e 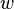 .
.
Capítulo 18 continha 103 versos em sânscrito que começou com regras para operações aritméticas envolvendo zero e de números negativos e é considerado o primeiro tratamento sistemático do assunto. As regras (que incluiu 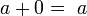 e
e 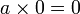 ) estavam todos corretos, com uma exceção:
) estavam todos corretos, com uma exceção: 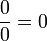 . Mais tarde no capítulo, ele deu a primeira solução explícita (embora ainda não completamente geral) da equação quadrática :
. Mais tarde no capítulo, ele deu a primeira solução explícita (embora ainda não completamente geral) da equação quadrática :
| " | Para o número absoluto multiplicado por quatro vezes o [coeficiente da] quadrado, adicionar o quadrado do [coeficiente da] médio prazo; a raiz quadrada da mesma, menos do [coeficiente do] médio prazo, sendo dividido por duas vezes o [do coeficiente] é o valor do quadrado. ( Brahmasphutasiddhanta (tradução Colebrook, 1817, página 346) | " |
Isto é equivalente a:
Também no capítulo 18, Brahmagupta foi capaz de fazer progressos na busca de soluções (integral) da equação de Pell,
onde 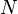 É um número inteiro não quadrado. Ele fez isso por descobrir a identidade seguinte:
É um número inteiro não quadrado. Ele fez isso por descobrir a identidade seguinte:
Identidade do Brahmagupta: 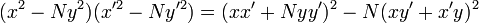 que era uma generalização de uma identidade anterior doDiofanto: Brahmagupta usou sua identidade para provar o seguinte lema:
que era uma generalização de uma identidade anterior doDiofanto: Brahmagupta usou sua identidade para provar o seguinte lema:
Lema (Brahmagupta):Se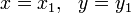 é uma solução de
é uma solução de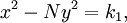 e,
e, 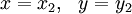 uma solução de
uma solução de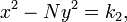 , em seguida:
, em seguida:
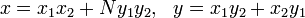 é uma solução de
é uma solução de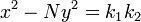
Ele então usou esse lema para ambos gerar um número infinito de soluções (integral) da equação de Pell, dada uma solução, e declarar o seguinte teorema:
Teorema (Brahmagupta):Se a equação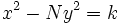 tem uma solução inteira para qualquer um dos
tem uma solução inteira para qualquer um dos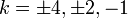 em seguida equação de Pell:
em seguida equação de Pell:
tem também uma solução inteira.
Brahmagupta não chegou a provar o teorema, mas funcionou exemplos usando seu método. O primeiro exemplo ele apresentou foi:
Exemplo (Brahmagupta):Encontre inteiros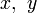 de tal modo que:
de tal modo que:
Em seu comentário, Brahmagupta acrescentou, "uma pessoa resolver este problema dentro de um ano é um matemático." A solução que ele foi fornecida:
- Bhaskara I
Bhaskara I (c. 600-680) expandiu o trabalho de Aryabhata em seus livros intitulado Mahabhaskariya , Aryabhattiya Bhashya e Laghu Bhaskariya . Ele produziu:
- Soluções de equações indeterminadas.
- Uma aproximação racional dafunção seno.
- Uma fórmula para calcular o seno de um ângulo agudo, sem a utilização de uma tabela, corrigir a 2 casas decimais.
Nono a décimo segundo Séculos
- Virasena
Virasena (9o século) foi um matemático Jaina no tribunal de Rashtrakuta Rei Amoghavarsha de Manyakheta, Karnataka. Ele escreveu o Dhavala , um comentário sobre a matemática Jaina, que:
- Lida com logaritmos basear 2 (ardhaccheda) e descreve suas leis.
- Primeiro usa logaritmos basear 3 (trakacheda) e base 4 (caturthacheda).
Virasena também deu:
- O cálculo dovolume dede umtronco de cone por um tipo de procedimento de infinito.
- Mahavira
Mahavira Acharya (c. 800-870) a partir de Karnataka, o último dos matemáticos Jaina notáveis, viveu no século nono e foi apadrinhado pelo rei Rashtrakuta Amoghavarsha. Ele escreveu um livro intitulado Ganit Saar Sangraha em matemática numérica, e também escreveu tratados sobre uma ampla gama de temas matemáticos. Estes incluem a matemática de:
- Zero.
- Praças.
- Cubos.
- raízes quadradas,raízes cúbicas, e asséries se estendem para além destes.
- Geometria plana.
- Geometria sólida.
- Problemas relacionados com o vazamento desombras.
- Fórmulas derivada para calcular a área de umaelipseequadrilátero dentro de umcírculo
Mahavira também:
- Afirmou que araiz quadradade umnúmero negativonão existia
- Deu a soma de umasérie cujos termos sãoquadrados de umaprogressão aritmética, e deu regras empíricas paraa áreaeperímetro de umaelipse.
- Equações cúbicas resolvido.
- Quárticas equações resolvido.
- Resolvido algumasequações de quinto grau e de ordem superiorpolinômios.
- Deu as soluções gerais das equações polinomiais de ordem superior:
- Resolvidos equações indeterminadas.
- Resolveu equações cúbicos indeterminados.
- Equações de ordem superior resolvidos indeterminados.
- Shridhara
Shridhara (c. 870-930), que viveu em Bengala, escreveu os livros intitulados Nav Shatika , Tri Shatika e Pati Ganita . Ele deu:
- Uma boa regra para encontrar ovolume dede umaesfera.
- A fórmula para resolverequações de segundo grau.
A Pati Ganita é um trabalho em aritmética e mensuração . Trata-se de várias operações, incluindo:
- Operações elementares
- Extraindo raízes quadradas e cúbicas.
- Frações.
- Oito regras dadas para as operações envolvendo zero.
- Métodos desomatório de diferentes aritmética e série geométrica, que viriam a se tornar referências normalizadas em obras posteriores.
- Manjula
Equações diferenciais de Aryabhata foram elaboradas no século 10 por Manjula (tambémMunjala), que percebeu que a expressão
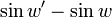
Pode ser expresso em aproximadamente
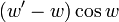
Ele entendeu o conceito de diferenciação depois de resolver a equação diferencial que resultou substituindo esta expressão na equação diferencial de Aryabhata.
- Aryabhata II
Aryabhata II (920-1000 c.) Escreveu um comentário sobre Shridhara, e um tratado astronômico Maha-Siddhanta . O Maha-Siddhanta tem 18 capítulos, e discute:
- Matemática numérica (Ank Ganit).
- Álgebra.
- Soluções de equações indeterminadas (kuttaka).
- Shripati
Shripati Mishra (1019-1066) escreveu os livros Siddhanta Shekhara , um importante trabalho sobre astronomia em 19 capítulos, e Ganit Tilaka , uma incompleta aritmética tratadistas em 125 versos com base em um trabalho de Shridhara. Ele trabalhou principalmente em:
- Permutações e combinações.
- Solução geral da equação linear simultânea indeterminado.
Ele também foi o autor deDhikotidakarana, uma obra de vinte versos sobre:
ODhruvamanasaé uma obra de 105 versos sobre:
- Calculando planetárioslongitudes
- eclipses.
- planetáriostrânsitos.
- Nemichandra Siddhanta Chakravati
Nemichandra Siddhanta Chakravati (c. 1100) o autor de um tratado matemático intituladoGome-mat Saar.
- Bhaskara II
Bhaskara II (1114-1185) foi um matemático-astrônomo que escreveu uma série de tratados importantes, nomeadamente a Siddhanta Shiromani , Lilavati , Bijaganita , Gola Addhaya , Griha Ganitam e Karan Kautoohal . Um número de suas contribuições foram posteriormente transmitidos para o Oriente Médio e Europa. Suas contribuições incluem:
Aritmética:
- Cálculo de juros.
- Progressões aritméticas e geométricas.
- Geometria plana.
- Geometria sólida.
- A sombra da gnomon.
- Soluções de combinações.
- Deu uma prova de divisão porzero,o serinfinito.
Álgebra:
- O reconhecimento de um número positivo que tem duas raízes quadradas.
- Surds.
- As operações com produtos de várias incógnitas.
- As soluções de:
- Equações de segundo grau.
- Equações cúbicas.
- Quárticas equações.
- Equações com mais do que um desconhecido.
- Equações de segundo grau com mais de um desconhecido.
- A forma geral deequação de Pell usando o chakravalamétodo.
- A equação quadrática indeterminado geral usando ochakravalamétodo.
- Equações cúbicas indeterminado.
- Quárticas equações indeterminado.
- De ordem superior indeterminadospolinomiaisequações.
Geometria:
- Deu uma prova doteorema de Pitágoras.
Cálculo:
- Concebido cálculo diferencial.
- Descoberto oderivado.
- Descoberto ocoeficiente diferencial.
- Desenvolvido diferenciação.
- Dito deteorema de Rolle, um caso especial doteorema do valor médio (um dos mais importantes teoremas de cálculo e análise).
- Derivado do diferencial da função seno.
- Computadorizadaπ, correta para 5 casas decimais.
- Calculou o comprimento da revolução da Terra em torno do Sol a nove casas decimais.
Trigonometria:
- Desenvolvimentos detrigonometria esférica
- As fórmulas trigonométricas:
Kerala Matemática (1300 - 1600)
O Kerala escola de astronomia e matemática foi fundada por Madhava de Sangamagrama em Kerala , sul da Índia e incluiu entre os seus membros: Parameshvara, Neelakanta Somayaji, Jyeshtadeva, Achyuta Pisharati, Melpathur Narayana Bhattathiri e Achyuta Panikkar. Ele floresceu entre os 14 e séculos 16 e as descobertas originais da escola parece ter terminado com Narayana Bhattathiri ( 1559- 1632). Na tentativa de resolver os problemas astronômicos, os astrônomos escola de Kerala independentemente criou uma série de conceitos matemáticos importantes. Os resultados mais importantes, expansão da série de funções trigonométricas , foram dadas em sânscrito versículo em um livro de Neelakanta chamado Tantrasangraha e um comentário sobre esta obra chamada Tantrasangraha-vakhya de autoria desconhecida. Os teoremas foram afirmou sem provas, mas as provas para a série de seno , cosseno , e inversa tangente foram fornecidos um século mais tarde no trabalho Yuktibhasa (c.1500-c.1610), escrito em Malayalam, por Jyesthadeva, e também em um comentário sobre Tantrasangraha .
A descoberta destes três expansões em séries importantes de cálculo séculos -Vários antes cálculo foi desenvolvido na Europa por Isaac Newton e Gottfried Leibniz -foi um marco na matemática. No entanto, a Escola de Kerala não pode ser dito ter inventado cálculo , porque, enquanto eles foram capazes de desenvolver expansões de séries de Taylor para as funções trigonométricas importantes, eles desenvolveram nem uma teoria abrangente de diferenciação ou integração , nem o teorema fundamental do cálculo . Os resultados obtidos pela escola Kerala incluem:
- O (infinito)série geométrica:
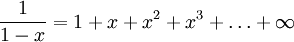 para
para 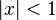 Esta fórmula já era conhecida, por exemplo, no trabalho do matemático árabe do século 10Alhazen (a forma latinizada do nome Ibn Al-Haytham (965-1039)).
Esta fórmula já era conhecida, por exemplo, no trabalho do matemático árabe do século 10Alhazen (a forma latinizada do nome Ibn Al-Haytham (965-1039)). - Uma prova semi-rigorosa (ver "indução" observação abaixo) do resultado:
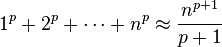 para grande n . Esse resultado também era conhecido por Alhazen.
para grande n . Esse resultado também era conhecido por Alhazen. - Uso intuitivo deindução matemática, no entanto, a hipótese indutivanão foi formulado ou empregados em provas.
- Aplicações de idéias de (o que viria a se tornar) diferencial e integralcalculusobter(Taylor-Maclaurin) série infinitade
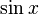 ,
, 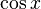 E
E 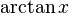 OTantrasangraha-vakhyadá a série em verso, que quando traduzido para a notação matemática, pode ser escrito como:
OTantrasangraha-vakhyadá a série em verso, que quando traduzido para a notação matemática, pode ser escrito como:
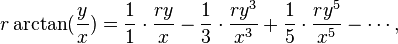 onde
onde 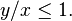
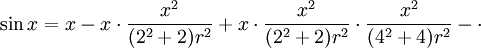
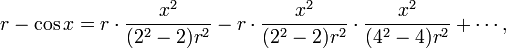 onde, para
onde, para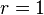 , a série reduzir à série de alimentação padrão para essas funções trigonométricas, por exemplo:
, a série reduzir à série de alimentação padrão para essas funções trigonométricas, por exemplo:
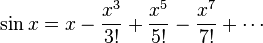 e
e 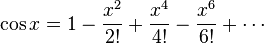
- Uso de rectificação (contagem do tempo) de um arco de círculo para dar uma prova destes resultados. (O método mais tarde de Leibniz, usando quadratura ( isto é, cálculo da área sob o arco de círculo, se não usado).
- Uso de expansão em série de
 obter uma série infinita de expressão (mais tarde conhecida como série Gregory) para
obter uma série infinita de expressão (mais tarde conhecida como série Gregory) para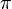 :
:
- A aproximação racional de erro para a soma finita de sua série de interesse. Por exemplo, o erro,
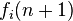 , (por N impar, e i = 1, 2, 3 ) para a série:
, (por N impar, e i = 1, 2, 3 ) para a série:
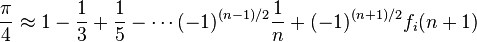
- onde
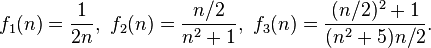
- onde
- Manipulação do termo de erro para derivar uma série de convergência mais rápida para
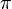 :
:
- Usando a série melhorou para derivar uma expressão racional,
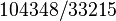 para
para 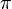 corrigir aténovecasas decimais,ou seja,
corrigir aténovecasas decimais,ou seja, 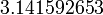
- Use de uma noção intuitiva de limite para calcular estes resultados.
- A semi-rigorosa (ver observação sobre os limites acima) método de diferenciação de algumas funções trigonométricas. No entanto, eles não formular a noção de uma função , ou ter conhecimento das funções exponenciais ou logarítmicos.
As obras da escola de Kerala foram escritos pela primeira vez para o mundo ocidental pelo inglês CM Whish em 1835 . De acordo com Whish, os matemáticos Kerala tinha " lançou as bases para um sistema completo de fluxões "e estas obras abundavam" com formas fluxional e séries a ser encontrado em nenhuma obra de países estrangeiros. " No entanto, os resultados da Whish foram quase completamente negligenciado, até mais de um século mais tarde, quando as descobertas da escola de Kerala foram investigados novamente por C. Rajagopal e seus associados. Seu trabalho inclui comentários sobre as provas da série arctan em Yuktibhasa dada em dois artigos, um comentário sobre a 'Yuktibhasa prova da série seno e cosseno s e de dois documentos que fornecem as sânscrito versos do Tantrasangrahavakhya para a série para arctan, o pecado e cosseno (com tradução para Inglês e comentários).
Os matemáticos Kerala incluído Narayana Pandit (c. 1340-1400), que compôs duas obras, um tratado aritmética, Ganita Kaumudi , e um tratado algébrica, Bijganita Vatamsa . Narayana também é pensado para ser o autor de um elaborado comentário de de Bhaskara II Lilavati, intitulado Karmapradipika (ou Karma-Paddhati ). Madhava de Sangamagramma (c. 1340-1425) foi o fundador da Escola de Kerala. Embora seja possível que ele escreveu Karana Paddhati um trabalho escrito em algum momento entre 1375 e 1475, todos nós sabemos realmente de seu trabalho vem de trabalhos de estudiosos posteriores.
Parameshvara (. C 1370-1460) escreveu comentários sobre as obras de Bhaskara I, Aryabhata e Bhaskara II. Sua Lilavati Bhasya , um comentário sobre de Bhaskara II Lilavati , contém uma das suas importantes descobertas: uma versão do teorema do valor médio. Nilakantha Somayaji (1444-1544) compôs o Tantra Samgraha (que ' desovado "mais tarde um comentário anônimo Tantrasangraha-vyakhya e mais um comentário do nome Yuktidipaika , escrito em 1501). Ele elaborou e estendeu as contribuições de Madhava.
Citrabhanu (c. 1530) foi um matemático do século 16 a partir de Kerala que deu soluções inteiras para 21 tipos de sistemas de duas equações algébricas simultâneas em duas incógnitas. Estes são os tipos de todos os possíveis pares de equações das sete formas seguintes:
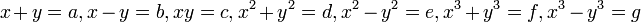
Para cada caso, Citrabhanu deu uma explicação e justificação de seu governo, bem como um exemplo. Algumas de suas explicações são algébrica, enquanto outros são geométricas. Jyesthadeva (c. 1500-1575) foi outro membro da Escola Kerala. Sua obra fundamental foi a Yukti-bhasa (escrito em Malayalam, uma língua regional de Kerala ). Jyesthadeva apresentou provas da maioria dos teoremas matemáticos e séries infinitas anteriormente descobertos por Madhava e outros matemáticos Kerala escola.
A acusação de eurocentrismo
Tem sido sugerido que as contribuições indianas para a matemática não ter sido dado o devido reconhecimento na história moderna e que muitas descobertas e invenções por matemáticos indianos são actualmente culturalmente atribuídos aos seus homólogos ocidentais, como resultado do eurocentrismo. De acordo com Joseph GG:
[O trabalho] tem em conta algumas das objecções levantadas sobre a trajetória eurocêntrica clássica. A consciência [de matemática indiana e árabe] é muito provável que ser temperado com rejeições não condiz com sua importância em relação a matemática grega. As contribuições de outras civilizações - nomeadamente a China ea Índia, são percebidos, quer como mutuários de fontes gregas ou tendo feito apenas contribuições menores ao desenvolvimento matemático mainstream. A abertura a resultados de pesquisas mais recentes, especialmente no caso da matemática indianos e chineses, é, infelizmente ausente "
O historiador da matemática,Florian Cajori, sugeriu que ele "suspeito [s] queDiofanto conseguiu seu primeiro vislumbre de conhecimento algébrico da Índia. "
Mais recentemente, como discutido na seção acima, a série infinita de cálculo para funções trigonométricas (redescoberto por Gregory, Taylor e Maclaurin no final do século 17) foram descritos (com provas) na Índia, por matemáticos da Escola de Kerala, notavelmente cerca de dois séculos antes. Alguns estudiosos têm sugerido recentemente que o conhecimento desses resultados pode ter sido transmitida para a Europa através da rota de comércio a partir de Kerala pelos comerciantes e missionários jesuítas. Kerala estava em contato permanente com China e Arábia, e, por volta de 1500, com a Europa. A existência de vias de comunicação e uma cronologia adequada certamente fazer tal transmissão uma possibilidade. No entanto, não há nenhuma evidência direta por meio de manuscritos relevantes que tal transmissão realmente ocorreram. Na verdade, de acordo com David Bressoud, "não há nenhuma evidência de que o trabalho indiano de série foi conhecida além da Índia, ou mesmo fora de Kerala, até o século XIX."
Ambos os estudiosos árabes e indianos fizeram descobertas antes do século 17 que agora são considerados uma parte do cálculo. No entanto, eles não foram capazes de, como Newton e Leibniz eram, para "combinar muitas idéias diferentes ao abrigo dos dois temas unificadores do derivado eo integrante , mostrar a conexão entre os dois, e vire cálculo para a grande ferramenta de resolução de problemas que temos hoje. " As carreiras intelectuais de Newton e Leibniz estão bem documentadas e não há nenhuma indicação de seu trabalho não ser seu próprio; no entanto, não se sabe com certeza se os imediatos antecessores de Newton e Leibniz ", incluindo, em particular, Fermat e Roberval, aprendemos de algumas das idéias dos matemáticos islâmicos e indianos através de fontes que não estão conscientes." Esta é uma área ativa de pesquisa atual, especialmente nos manuscritos coleções de Espanha e Magrebe , a investigação que está agora a ser prosseguido, entre outros lugares, no Centro Nacional de Pesquisa Científica, em Paris .